基于狄利克雷混合模型的图像分类算法研究
2021-11-16曹会蕊关文博杨帆
曹会蕊 关文博 杨帆
(北方工业大学信息学院,北京 100144)
0 引言
概率混合模型是重要的统计建模工具,在人工智能领域得到了极其广泛的应用。在实际应用中,通常采取高斯分布的假设来构建概率混合模型。然而大量研究表明,现实中的很多数据具有非高斯特性。近年来,数据的非高斯建模得到了国内外学者的广泛关注。狄利克雷混合模型[1]就是一种典型的非高斯混合模型,国内外学者对其展开了比较深入的研究,并且将其应用于解决图像分类、目标检测、文本分类等问题。
在狄利克雷混合模型的实际应用中,模型学习是一项非常重要的工作,主要包括估计模型参数和确定混合分量数。目前狄利克雷混合模型的学习方法主要有变分推理(Variational Inference)、马尔科夫链蒙特卡洛(Markov Chain Monte Carlo)、期望传播(Expectation Propagation)等。然而这些方法每次迭代优化过程中都需要对全体训练集进行计算,因此无法处理大规模数据或者动态流数据,无法在实际应用中推广。
针对变分推理的这些缺点,Hoffman等[2]提出了随机变分推理(Stochastic Variational Inference),它结合了重采样和自然梯度优化方法,是针对海量数据集的概率模型的高效学习方法。国内关于随机变分推理的研究处于起步阶段,如柴变芳等[3]利用随机变分推理研究了基于概率模型的大规模网络结构发现方法,蒋晓娟等[4]利用随机变分推理研究了加权网络的在线结构学习算法。国外关于随机变分推理的研究发展比较迅速,随机变分推理已经被广泛应用于许多类型的模型,包括主题模型[5]、统计网络分析[6]、过程因子分析[7]、层次狄利克雷过程-隐马尔可夫模型[8]、贝叶斯时间序列模型[9]、大规模离散选择模型[10]等。
本文针对狄利克雷混合模型的随机变分推理算法展开深入的研究,对其提出完备的随机变分学习框架,进而将其成功应用于解决图像分类问题,实验结果证明了该算法的有效性和可行性。
1 狄利克雷混合模型

2 模型推理与学习

狄利克雷混合模型的具体方法流程如下:
(1)选择一个恰当的混合分量数,初始化混合分量I;(2)初始化C0,α0,μ0;(3)利用K-means算法初始化rsi;(4)从N个样本中随机采样S个样本;(5)利用式(14)更新抽样数据的局部变分参数;(6)利用式(16)、式(17)和式(18)更新中间全局变分参数;(7)利用式(19)、式(20)和式(21)更新全局变分参数;(8)重复第4、5、6、7这四步直至收敛。
3 图像自动分类
将上述狄利克雷混合模型用于图像分类的应用场景中,本文采用两个公共可获得的图像数据集来测试上述提出算法的有效性和可行性。第一个图像数据集是Caltech4,第二个图像数据集由两类图像组成:Georgia Tech人脸和非人脸背景图。
对于上述数据集中的每类图像,选取一半作为训练集,另一半作为测试集,重复20次实验。对比本文提出的方法(记为SVI-DMM)与基于单下界(Single Lower Bound,SLB)近似策略的狄利克雷混合模型的变分推断方法[1](记为VI-DMMSLB)以及基于多下界(Multiple Lower Bound,MLB)近似策略的狄利克雷混合模型的变分推断方法的性能[11](VI-DMMMLB)。见表1与表2。
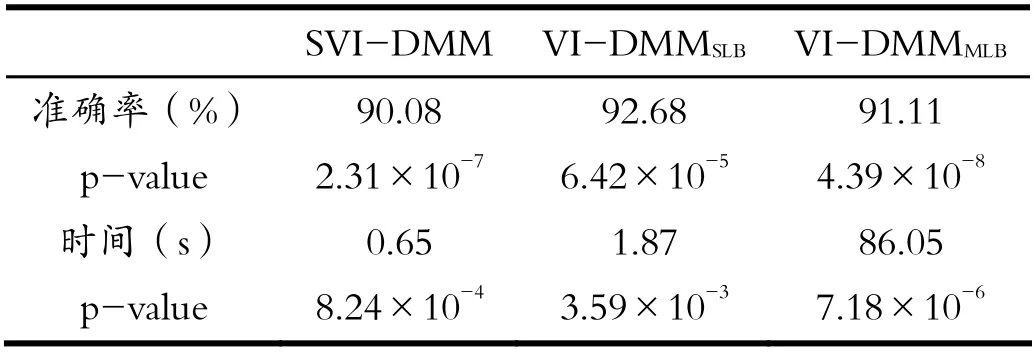
表1 图像数据集1:分类准确率(%)、时间(s)、p-value 对比Tab.1 Image dataset 1: comparison of classification accuracy (%),time (s) and p-value

表2 图像数据集2:分类准确率(%)、时间(s)、p-value 对比Tab.2 Image dataset 2: comparison of classification accuracy (%),time (s) and p-value
由表1与表2可以看出,本文提出的狄利克雷混合模型的随机变分推断方法是有效的,虽然在识别率上低于另外两种方法,但是其最大的优势是计算成本较低,并且不会随着数据量的增多而有大幅度的变化,适用于大规模数据。
4 结语
本文针对狄利克雷混合模型提出了一种有效的随机变分推理算法,首先,通过下界近似策略找到了抽样数据的变分目标函数的下界函数;其次,通过最大化该下界函数,求解出局部变分参数和中间局部变分参数的解析解表达式;最后,采用随机优化的方法,求解出全局变分参数的解析解表达式。通过实际数据集验证了该算法的高效性。
