上海地区不同强度参数对基坑围护结构变形和内力的影响
2021-11-13王卫东徐中华
何 平,王卫东,徐中华,王 强
(1. 中冶赛迪上海工程技术有限公司,上海 200940; 2. 华建集团上海地下空间与工程设计研究院,上海 200011;3. 上海基坑工程环境安全控制工程技术研究中心,上海 200011)
0 引 言
平面竖向弹性地基梁法广泛应用于基坑围护结构的变形和内力分析。该方法将单位宽度的围护结构作为竖向放置的弹性地基梁,围护结构外侧作用水土压力,坑内开挖面以下土体采用弹簧模拟,支撑和锚杆简化为与截面面积、弹性模量、计算长度等有关的弹簧单元,计算示意图如图1所示。为了工程应用方便,土压力常采用朗肯主动土压力理论,且假设开挖面下土弹簧刚度沿深度线性增加,即上海市《基坑工程技术标准》(DG/TJ 08-61—2018)[1]和行业规范《建筑基坑支护技术规程》(JGJ 120—2012)[2]推荐采用的m法。
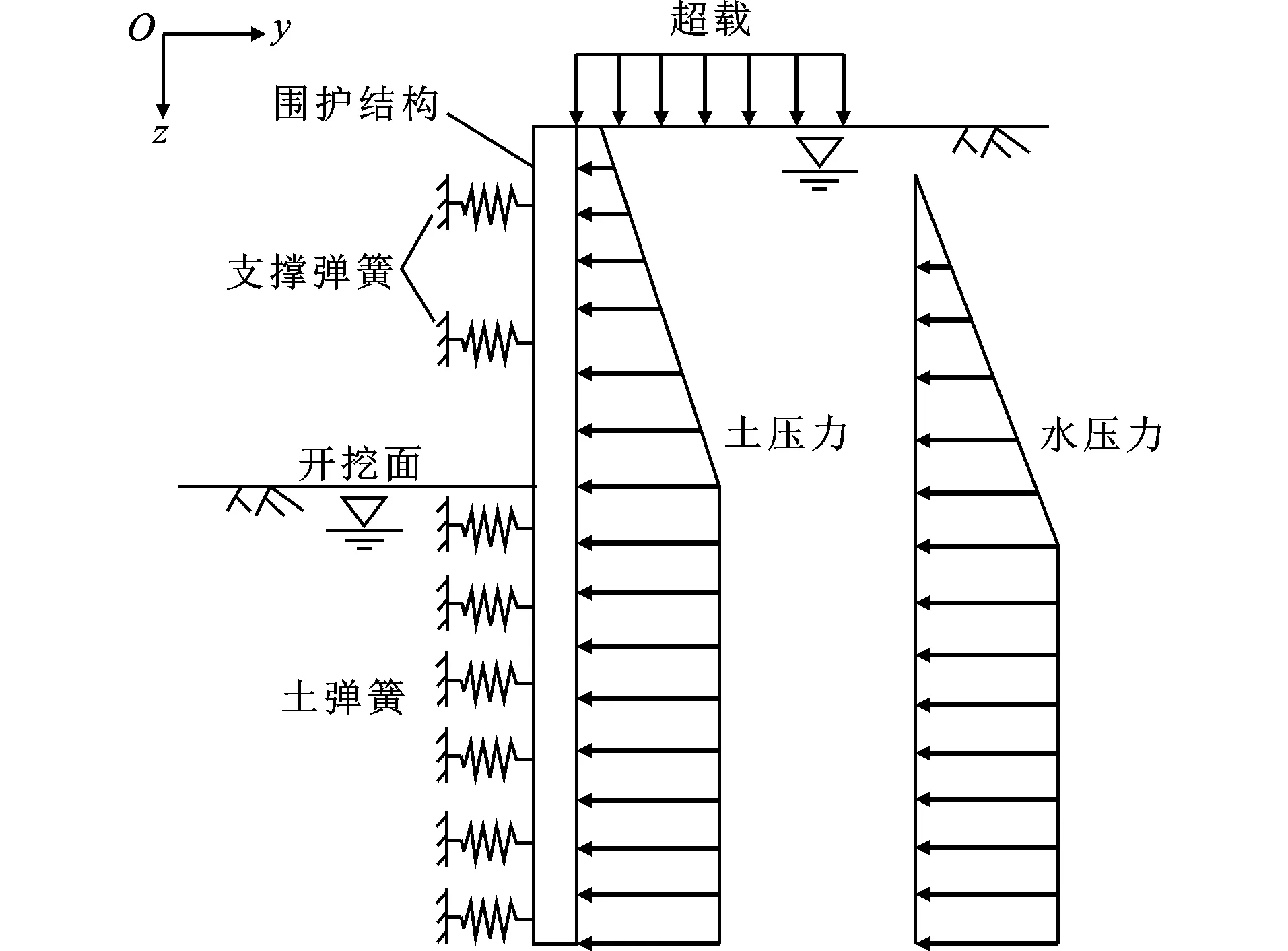
图1 平面竖向弹性地基梁法示意图Fig.1 Schematic Diagram of Plane Vertical Elastic Foundation Beam Method
根据温克尔弹性地基梁模型可知,围护结构在侧向荷载(水土压力)和弹簧抗力的相互作用下静力平衡。从上述方法可以看出,围护结构外侧的水土压力对围护结构变形和内力具有重要影响。对于水土压力,根据土层的特性存在2种不同的计算模式,即水土分算和水土合算[3]。水土分算原则是基于土力学有效应力原理,将土压力与水压力分开计算,采用有效应力强度参数,但在实际应用中很难确定黏土中的孔隙水压力,而且一般地质勘察报告也不提供有效应力强度参数,因此在这种情况下,习惯将水土压力混合计算(采用总应力强度参数),并称之为水土合算原则。由于水土分算概念明确,符合有效应力原理,因此现行上海市基坑规范《基坑工程技术标准》(DG/TJ 08-61—2018)[1]规定水土压力计算采用的是水土分算方法。工程界对于基坑工程中围护结构侧压力采用水土分算还是水土合算仍然存在很大争议,很多学者[4-7]对此进行了研究,为解决水土分算和合算之间的争议,有学者[8-9]还提出了水土分算和合算的统一算法。
无论是采用水土分算还是合算,土压力计算中都需要用到土体的强度参数。一般来说,水土分算应采用有效应力强度参数,水土合算应采用总应力强度参数,但对不同土类应采用何种强度参数计算土压力仍存在争议[10-13]。张其光等[14]通过研究指出,水土分算概念明确,考虑到基坑开挖的实际应力路径,可采用减压三轴固结不排水压缩试验(RTC)总应力强度参数指标来计算水土压力,解决了无法确定超静孔压的问题,而且计算结果比较符合实际情况。高广运等[15]根据上海某软土工程试验资料,对比分析了不同试验方法抗剪强度指标计算基坑土压力的变化,建议在基坑支护结构设计中土压力计算应采用固结不排水强度指标,当有可靠工程经验时,也可采用直剪固结快剪强度指标。Ou[16]建议在考虑黏性土短期行为时可采用总应力方法计算土压力,即使用不排水抗剪强度参数,并应适当考虑土壤和挡土墙之间的摩擦力。马郧等[17]以武汉长江Ⅰ级阶地中海国际大厦超深基坑工程为研究背景,指出当选取固结不排水抗剪强度指标时,地下连续墙水平位移和地层土压力更接近实测数据,直剪固结快剪指标次之。刘秀秀等[18]指出对于软土基坑支护结构设计采用三轴不固结不排水试验指标比较安全,但随着深度的增大,偏于保守将造成不必要的浪费。高彦斌等[19]指出将三轴固结不排水抗剪强度指标和直剪固结快剪强度指标代入朗肯土压力计算公式是一种错误的分析方法,由此导致了对水土合算土压力分析方法的误解,并给出了基坑开挖卸载下正确的水土合算土压力计算公式。
上述研究大多数属于定性研究,不但包含的强度参数较少,而且实际工程中有效应力强度参数较难获取。因此上海市基坑规范《基坑工程技术标准》(DG/TJ 08-61—2018)[1]虽然采用水土分算方法,但在设计中还是采用直剪固结快剪强度参数ccq,φcq或三轴固结不排水(CU)总应力强度参数ccu,φcu来计算土压力,这与有效应力原理相悖。这种经验上的处理与理论方法之间究竟存在多大差异不甚清楚,因此定量给出不同强度参数对基坑围护结构变形和内力的影响具有重要的工程意义。
本文利用ABAQUS软件建立平面竖向弹性地基梁法模型,根据上海地区4类典型基坑概化模型和土层强度参数,研究了不同土体强度参数(直剪固结快剪总应力强度参数ccq,φcq;三轴固结不排水(CU)总应力强度参数ccu,φcu;十字板不排水抗剪强度su;三轴固结不排水试验有效应力强度参数c′,φ′)对围护结构变形和内力的影响,为相关基坑设计强度参数的选择提供参考,具有重要的实际工程意义。
1 ABAQUS平面竖向弹性地基梁法
为了研究不同强度参数对围护结构变形和内力的影响,结合有限元软件ABAQUS建立了基坑工程平面竖向弹性地基梁法模型,如图2所示。其中,围护结构采用B21梁单元模拟,支撑弹簧和土抗力弹簧分别采用弹簧单元Spring2和土弹簧单元Spinga模拟。该模型可以考虑水土分算和水土合算,土弹簧刚度和侧向水土压力荷载随开挖过程的变化采用子程序Subroutine实现。土弹簧的刚度变化采用子程序Ufiled场变量实现,水土压力的变化采用子程序Dload来实现,程序的具体案例验证可参见文献[20]。

图2 ABAQUS平面竖向弹性地基梁法模型Fig.2 Plane Vertical Elastic Foundation Beam Method Model in ABAQUS
何平等[21]根据ABAQUS平面竖向弹性地基梁法模型分析了均质土层中强度参数(黏聚力和内摩擦角)对围护结构变形和内力的影响,指出无论是采用水土分算还是水土合算,随着黏聚力和内摩擦角的增大,围护结构的变形和内力都随之减小。同一强度参数下,水土分算的结果要大于水土合算,随着黏聚力的增大,水土分算和合算计算结果的曲线基本平行,但随着内摩擦角的增大,水土分算和合算结果曲线之间的差异越来越大。实际工程中土层都非均质,因此需要研究成层土中不同强度参数对围护结构变形和内力的影响。
2 上海地区典型基坑概化模型
上海属于软土地区,基坑开挖易产生较大变形,常采用板式支护结构。王浩然[22]对上海地区62个板式支护体系的基坑开挖深度、支撑道数和围护结构插入比进行了统计,提出可将上海地区的基坑分为A,B,C,D四种类型,具体如下所述。
A类:基坑的开挖深度一般小于7 m,围护结构一般采用钻孔灌注桩,常采用1道支撑支护,围护结构底部一般位于软弱的第④层淤泥质黏土层,围护结构插入比范围为1.2~2.01。
B类:基坑的开挖深度一般为7~12 m,围护结构一般采用钻孔灌注桩,坑内采用2道支撑支护,围护结构一般需穿越软弱的淤泥质黏土层,进入第⑤层黏土或更深的土层中,插入比范围为1.05~1.52。
C类:基坑的开挖深度一般为12~16 m,围护结构一般采用钻孔灌注桩或地下连续墙,坑内采用3道支撑支护,围护结构一般进入第⑤2,⑤3,⑤4等土层中,插入比范围为0.91~1.11。
D类:基坑开挖深度一般为16~23 m,围护结构一般采用地下连续墙,坑内采用4道支撑支护,围护结构基本进入土层条件较好的第⑥层黏土或第⑦层粉细砂,插入比范围为0.70~0.93。
从上述基坑分类可看出,随着基坑开挖深度的增加,插入比逐渐减小,支撑的道数逐渐增加。根据上述4种典型基坑分类建立了相应的基坑概化计算模型。其中,A类计算模型开挖深度He=6 m,围护结构深度Hw=15 m,插入比为1.5,采用1道支撑;B类计算模型开挖深度He=11 m,墙体深度Hw=24 m,插入比为1.2,采用2道支撑;C类计算模型基坑开挖深度He=16 m,墙体深度Hw=32 m,插入比为1.0,采用3道支撑;D类计算模型基坑开挖深度He=21 m,墙体深度Hw=42 m,插入比为1.0,采用4道支撑。所有计算模型的首层土开挖深度为1.5 m,首道支撑均位于地表以下1 m处,支撑竖向间距均为5 m。坑外水位设为地表以下1 m,坑内水位设与开挖面平齐,具体概化模型如图3所示。

图3 上海典型基坑概化模型Fig.3 Typical Generalization Models of Excavations in Shanghai
3 不同强度参数对围护结构变形和内力的影响
3.1 土层和支撑围护结构参数
表1给出了计算模型中的土层参数。由于上海地区第①层杂填土厚度较小,为1~2 m,为了简化计算,将第①层杂填土和第②层粉质黏土合并为一层土并取第②层土体的计算参数。计算模型中各土层厚度根据上海地区典型土层分层近似取得,各层土重度和强度参数来源于文献[20]中根据195个工程勘察报告和文献试验数据统计得到的上海地区各典型土层统计结果的平均值。强度参数考虑了3组总应力强度参数(直剪固结快剪ccq,φcq;三轴固结不排水ccu,φcu;十字板不排水抗剪强度su)和1组有效应力强度参数(三轴固结不排水c′,φ′)。第⑤层土为第⑤1层粉质黏土和第⑤3层粉质黏土统计结果的平均值,第⑦层粉细砂结果为根据实际工程中的经验得到。值得一提的是,由于第⑦层土为粉砂层,且只有D类计算模型围护结构到达第⑦层土深度处,因此对计算结果影响不大,所以假设第⑦层土的强度参数一致,均为有效应力强度参数。各层土的土体基床比例系数m值根据上海市《基坑工程技术标准》(DG/TJ 08-61—2018)[1]给出的不同类型土经验范围取值估计得到。
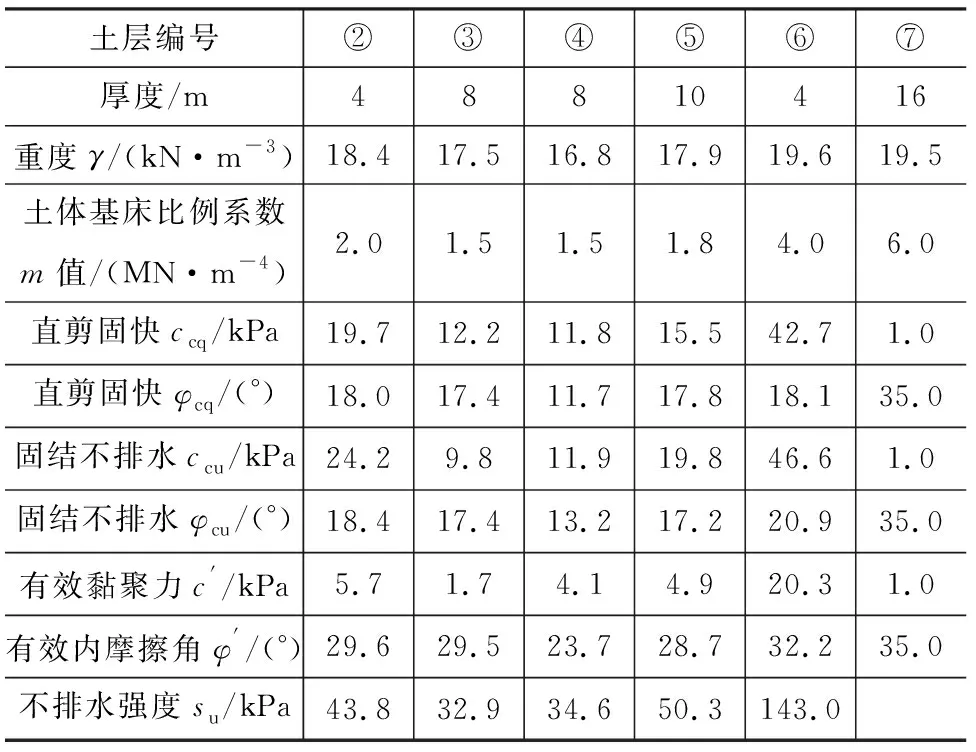
表1 土层计算参数Table 1 Calculation Parameters of Soil Layers
表2给出了不同计算模型中围护结构的抗弯刚度EI、抗压刚度EA以及支撑的刚度参数。对于A类计算模型,由于开挖深度较浅,实际工程中一般采用直径800 mm的钻孔灌注桩作为围护结构,此处为了统一,将直径800 mm的钻孔灌注桩等效成每延米相同抗弯刚度的620 mm厚地下连续墙(刚度等效原则,上海地区桩净距一般为200 mm);对于B类、C类和D类计算模型,围护结构分别采用800,800,1 000 mm厚的地下连续墙。
计算模型中的支撑均采用钢筋混凝土支撑,并且假设同一类计算模型中的各道支撑截面均相同,支撑截面尺寸均根据上海地区典型基坑支护方法估计得到。在计算模型中,需要确定支撑弹簧的刚度KB=2EA/(Ls),其中,E为支撑材料的弹性模量,A为支撑的截面面积,L为支撑计算长度,s为支撑水平间距。根据上海地区典型基坑数据,支撑的水平间距s一般为9 m,基坑的宽度L设为100 m,计算得到的支撑刚度见表2。

表2 围护结构和支撑系统计算参数Table 2 Calculation Parameters of Retaining Structures and Support Systems
3.2 分析工况
4种基坑计算模型中的开挖步骤具体如下所述。
Step1:悬臂开挖至地下1.5 m。
Step2:施工第1道支撑(地表下1 m处)并开挖至下道支撑以下0.5 m。
Step3:重复Step2直至开挖结束。
以C类计算模型为例,表3给出了详细的计算步骤,坑外考虑20 kPa的超载。

表3 C类模型的计算步骤Table 3 Calculation Steps of Model C
3.3 计算结果
为了分析不同强度参数对围护结构内力和变形的影响,每个计算模型的强度参数分别采用4种不同的强度指标:直剪固结快剪总应力强度参数ccq,φcq;三轴固结不排水试验总应力强度参数ccu,φcu;原位十字板不排水抗剪强度su(黏聚力c=su,内摩擦角φ=0°);三轴固结不排水试验有效应力强度参数c′,φ′。根据上海市《基坑工程技术标准》(DG/TJ 08-61—2018)[1]规定,上海地区基坑设计采用水土分算方法,为了与土力学有效应力原理保持一致,采用水土分算时应采用有效应力强度参数指标,因此不同强度参数比较结果均以有效应力强度参数计算结果为基准。
以C类基坑计算模型为例,图4~7给出了以有效应力强度参数为计算参数的不同开挖阶段的围护结构侧向位移、弯矩和剪力结果,支撑轴力结果如表4所示。采用其他3种强度参数的有限元计算结果形式类似,因此不再赘述,与有效应力强度参数计算结果的比较见表5。

表4 C类模型不同开挖阶段的支撑轴力Table 4 Support Axial Forces at Different Excavation Stages of Model C
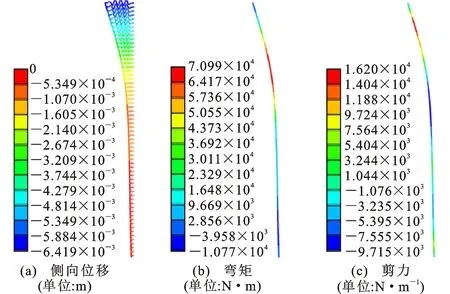
图4 C类模型Step1结果Fig.4 Results of Step1 for Model C

图5 C类模型Step2结果Fig.5 Results of Step2 for Model C

图6 C类模型Step3结果Fig.6 Results of Step3 for Model C
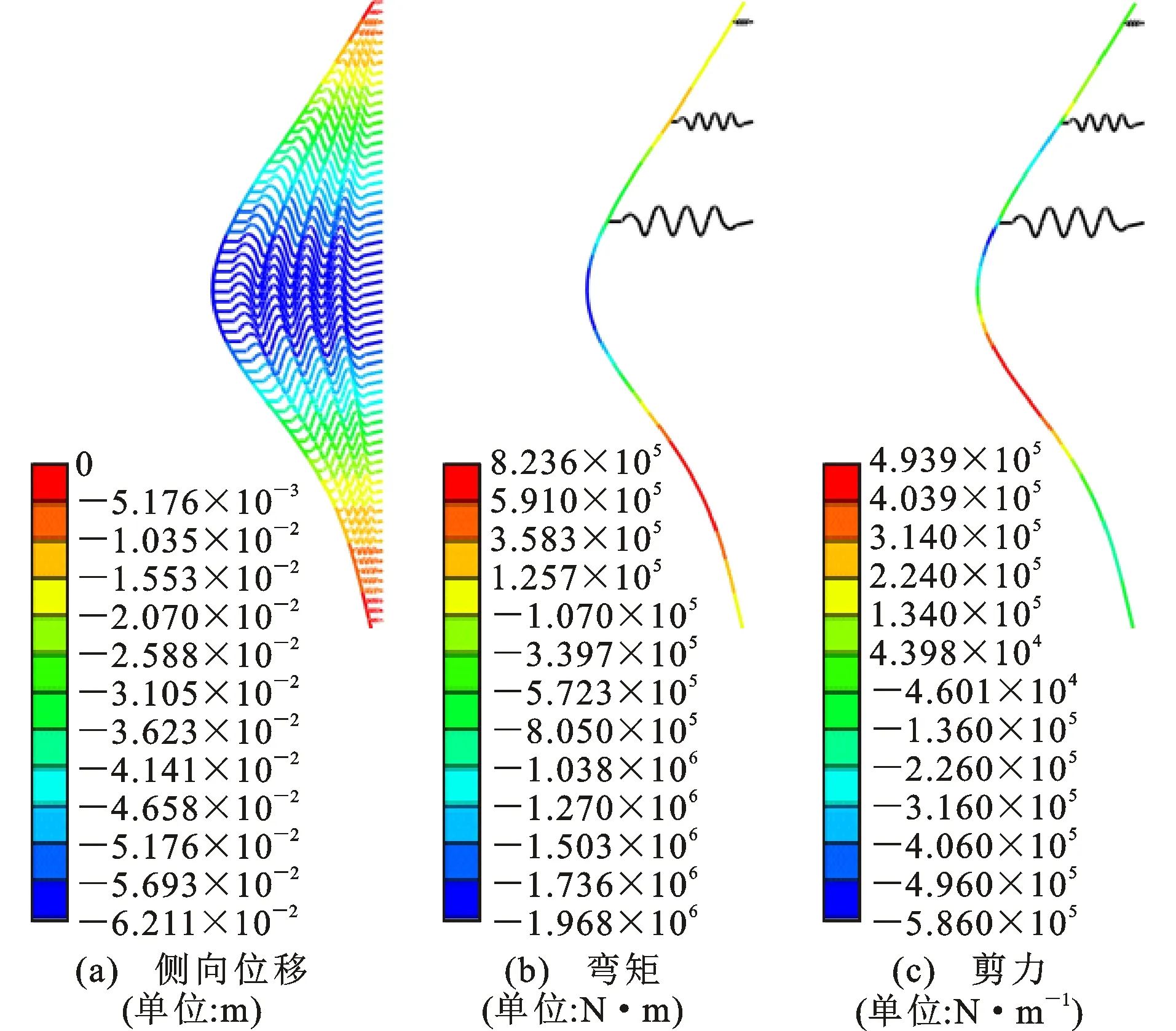
图7 C类模型Step4结果Fig.7 Results of Step4 for Model C
从图4~7中围护结构侧向位移变化曲线可知,在Step1第1工况时,即悬臂开挖阶段,围护结构位移曲线呈现出悬臂分布的形式。随着深度的增加,侧向位移逐渐减小,最大侧向位移位于地表,约为6.4 mm,为开挖深度He的0.63%;随着开挖的加深及支撑的设置,在随后的3个工况下,围护结构的侧向位移呈现鼓胀型分布曲线,这也是多支撑体系基坑开挖围护结构典型的变形曲线。最大侧向位移随着开挖深度的加深逐渐增大,如Step2中最大侧向位移约为22.3 mm,为开挖深度的0.34%;Step3最大侧向位移为48.7 mm,约为开挖深度的0.42%;Step4最大侧向位移为76.5 mm,约为开挖深度的0.48%。除第1阶段外,最大侧向位移位置均发生在开挖面附近。
从弯矩图中可以看出,不同开挖阶段的弯矩分布形式不同,在同一工况中开挖面处弯矩最大,不同工况下最后工况产生的弯矩最大。从剪力图中可以看出,在支撑位置处由于支撑的设置剪力产生突变,最后开挖阶段产生的剪力最大。
从表4中各开挖工况下支撑轴力可以看出,第1道支撑的轴力在Step2中最大,随着开挖深度的加深和第2道、第3道支撑的设置,第1道支撑的轴力逐渐减小,而第2道支撑在Step4中轴力加大。最大支撑轴力中,第3道支撑最大,其次为第2道支撑,最小为第1道支撑。
3.4 基坑概化模型统计结果
对4种基坑概化模型分别采用不同的强度参数计算得到的围护结构变形和内力结果见表5~8,其中括号内数据表示以有效应力强度参数计算结果为基准的增量百分比。
从表5~8可以看出,除了A类模型外,其他3类模型中各种强度参数相比有效应力强度参数的增量百分比大部分为正,说明采用有效应力强度参数得到的结果最小。因此,若基坑挖深较大,设置2道支撑以上的普遍情况下,采用有效应力强度参数计算得到的围护结构变形和内力最小。从表5~8还可以看出,直剪固结快剪总应力强度参数和CU总应力强度参数得到的结果较为接近,这可能也是上海市《基坑工程技术标准》(DG/TJ 08-61—2018)[1]提出可采用直剪或CU总应力强度参数计算土压力的原因。进一步分析可发现,直剪和CU总应力强度参数计算得到的围护结构变形和内力与有效应力强度参数的结果相比,最大弯矩和剪力增量为7%~8%,最大位移增量约为6%。采用原位十字板不排水抗剪强度su得到的结果增量在不同的基坑模型中有正有负,规律不明显,无法得到明显的结论,但整体而言大于有效应力强度参数结果。
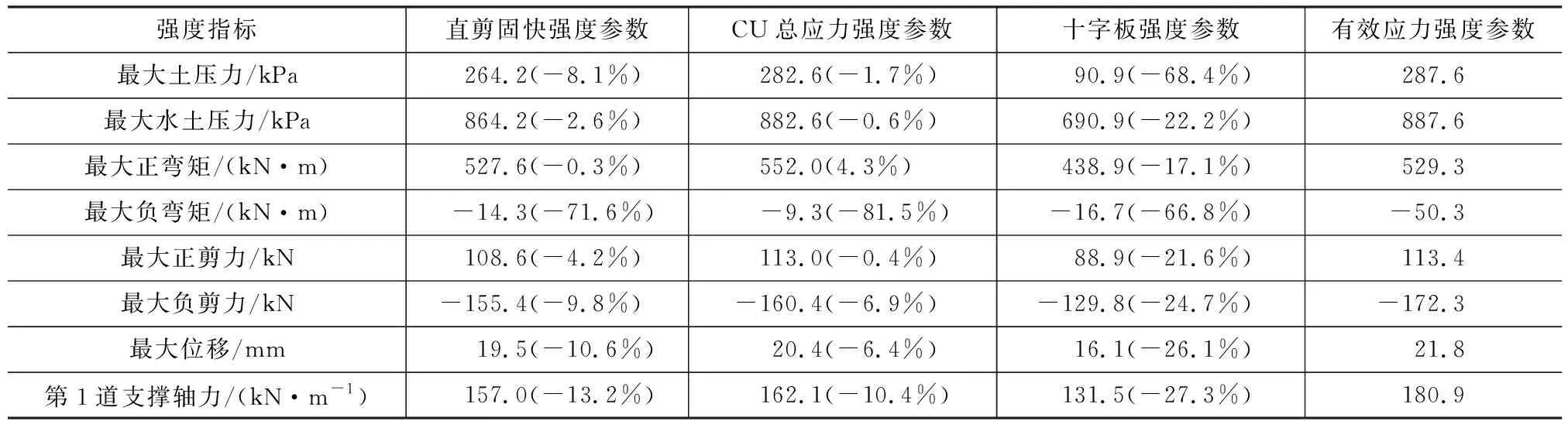
表5 A类模型不同强度参数下围护结构内力和变形结果Table 5 Results of Deformation and Internal Force of Retaining Structure by Using Different Strength Parameters for Model A
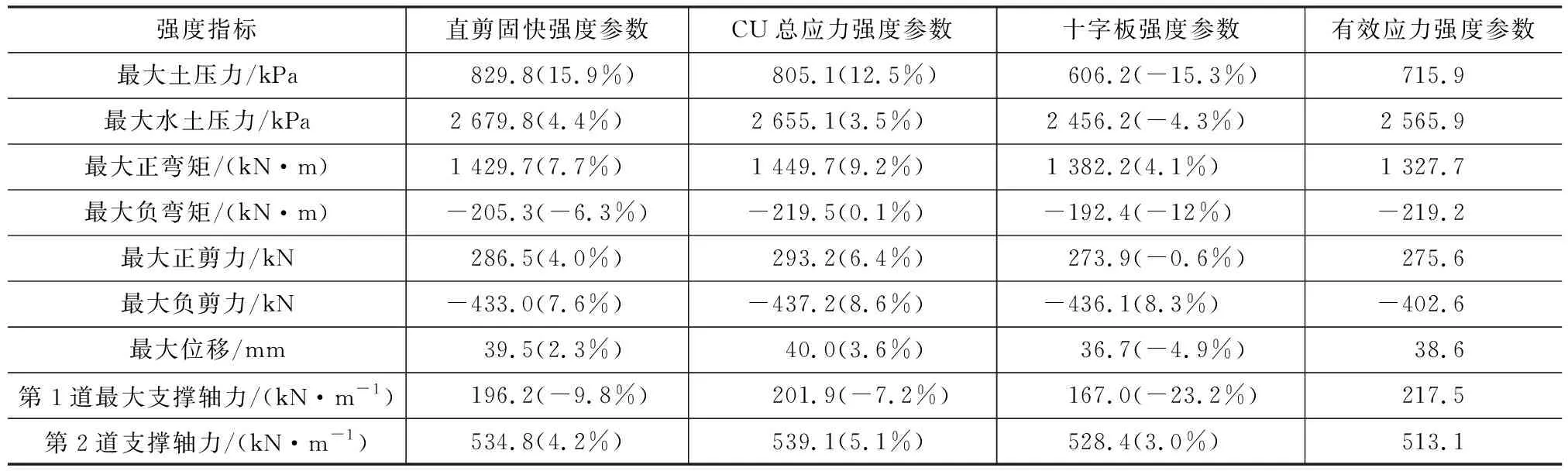
表6 B类模型不同强度参数下围护结构内力和变形结果Table 6 Results of Deformation and Internal Force of Retaining Structure by Using Different Strength Parameters for Model B
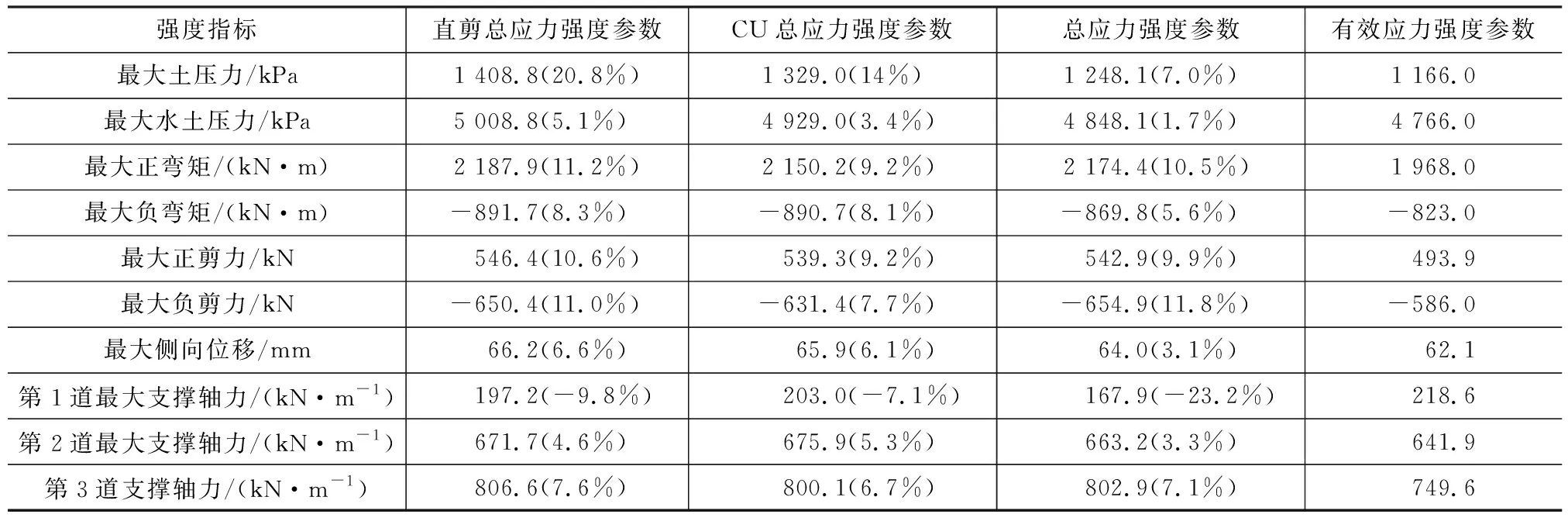
表7 C类模型不同强度参数下围护结构内力和变形结果Table 7 Results of Deformation and Internal Force of Retaining Structure by Using Different Strength Parameters for Model C
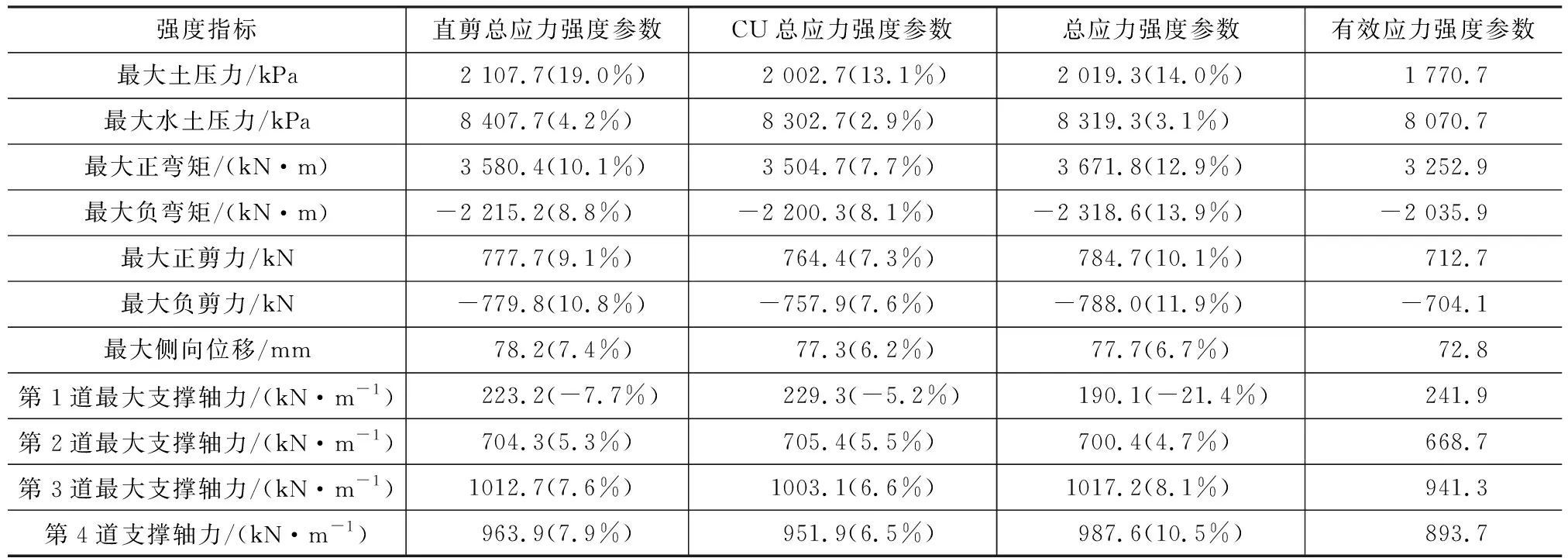
表8 D类模型不同强度参数围护结构内力和变形结果Table 8 Results of Deformation and Internal Force of Retaining Structure by Using Different Strength Parameters for Model D
4 结 语
(1)水土分算时,采用有效应力强度参数得到的围护结构变形和内力最小,采用直剪固快和CU总应力强度参数计算得到的最大位移相比有效应力强度参数结果平均增量约为6%,最大水土压力平均增量为4%~5%,最大弯矩和剪力平均增量为7%~8%。采用十字板不排水抗剪强度参数su计算无法得出明显规律。
(2)水土分算时,采用不同强度参数计算得到的土压力差别较大,但在考虑了水压力后,不同强度参数计算得到的侧向荷载差异变小,这说明了水土分算中水压力比土压力所占比例更大,对围护结构变形和内力影响更大。
(3)上海市《基坑工程技术标准》(DG/TJ 08-61—2018)采用的水土分算概念明确,理论上强度参数应优先采用有效应力强度参数,当缺乏数据时,可按CU总应力强度参数、直剪固快强度参数顺序选取,这2种强度参数计算结果相比有效应力强度参数结果偏安全。
