EXISTENCE TO FRACTIONAL CRITICAL EQUATION WITH HARDY-LITTLEWOOD-SOBOLEV NONLINEARITIES∗
2021-11-13
Department of Mathematics,Razi University,Kermanshah,Iran E-mail:nyamoradi@razi.ac.ir;neamat80@yahoo.com
Abdolrahman RAZANI
Department of Pure Mathematics,Faculty of Science,Imam Khomeini International University,34149-16818,Qazvin,Iran E-mail:razani@sci.ikiu.ac.ir
Abstract In this paper,we consider the following new Kirchhoff-type equations involving the fractional p-Laplacian and Hardy-Littlewood-Sobolev critical nonlinearity:whereis the fractional p-Laplacian with 0
Key words Hardy-Little wood-Sobolev inequality;concentration-compactness principle;variational method;Fractional p-Laplacian operators;multiple solutions
1 Introduction
In this paper,we study the multiplicity of solutions to the following Kirchhoff-type equations with Hardy-Little wood-Sobolev critical nonlinearity:
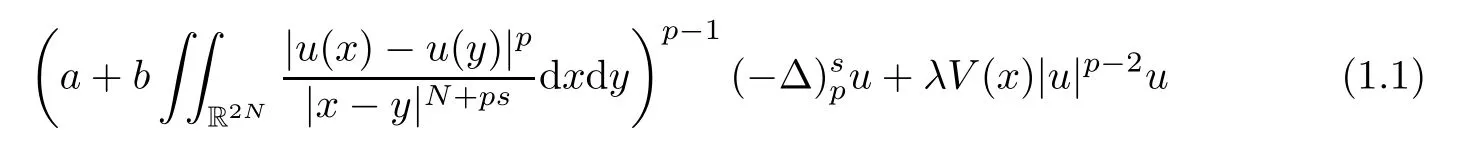

So,the main result of this paper can be included in the following theorem:
Theorem 1.1Assume that(V1)and(V2)hold.Then,(1.1)has in finitely many solutions forsp We point out that Theorem 1.1 extends Theorem 2.4 in[21]to the casea=1,b=0,p=2 and Theorem 1.1 in[14,17,32]to the casep=2 ands=1. We firstly recall that the fractional Kirchhoff equation was first introduced and motivated in[6].The study of existence and uniqueness of positive solutions for Choquard type equations attracted a lot of attention of researchers due to its vast applications in physical models[26].Fractional Choquard equations and their applications is very interesting;we refer the readers to[3,7,8,13,18,21,22,27,35,37]and the references therein.The authors in[27],by using the Mountain Pass Theorem and the Ekeland variational principle,obtained the existence of nonnegative solutions of a Schrdinger-Choquard-Kirchhoff-type fractionalp-equation.Ma and Zhang[18]studied the fractional order Choquard equation and proved the existence and multiplicity of weak solutions.In[7],the authors investigated a class of Brzis-Nirenberg type problems of nonlinear Choquard equation involving the fractional Laplacian in bounded domainΩ.Wang and Yang[36],by using an abstract critical point theorem based on a pseudo-index related to the cohomological index,studied the bifurcation results for the critical Choquard problems involving fractionalp-Laplacian operator: where Ω is a bounded domain in RNwith Lipschitz boundary andλis a real parameter.Also,in[11,23,29],the authors studied the existence of multiple solutions for problem(1.3),whenp=2.For more works on the Brezis-Nirenberg type results on semilinear elliptic equations with fractional Laplacian,we refer to[29,30,33]and references therein. On the other hand,Song and Shi in[31]studied the following Kirchhoff equations with Hardy-Littlewood-Sobolev critical nonlinearity: The proofs of our main results are obtained by applying variational arguments inspired by[25,31]. The paper is organized into three sections.In Section 2,we recall some basic de finitions of fractional Sobolev space and Hardy-Littlewood-Sobolev Inequality,and we give some useful auxiliary lemmas.In Section 3,we give the proof of Theorem 1.1. Let 0 equipped with the norm De fine the space with the norm Lemma 2.1(see[25,Lemma 1])(Xλ,‖·‖Xλ)is a uniformly convex Banach space. Lemma 2.2(see[25,Lemma 2])Assume that(V1)holds.Then the embeddingsXλWs,p(RN)Lν(RN)are continuous forν∈[].In particular,there exists a constantCν>0 such that Moreover,for anyR>0 andν∈[1]the embeddingXλLν(BR(0))is compact. Also,letSp,Hbe the best constant andS∗be the best Sobolev constant Now,we recall that a sequence{(un,vn)}is a Palais-Smale sequence at the levelc((PS)csequence in short)for the functionalJifJ(un,vn)→candJ′(un,vn)→0.If any(PS)csequence{(un,vn)}has a convergent subsequence,we say thatJsatis fies the(PS)ccondition. Lemma 2.5Assume that(V1)and(V2)hold.ThenJλ,Vsatis fies the(PS)ccondition for allsp So,{un}nis bounded inXλ. Then,there exists a subsequence,still denote by{un},such thatun⇀uweakly inXλ.Also,in view of Lemma 2.2 and Lemma 2.3,we have So,(2.16)and(2.17)imply that Here,similar to the method in[25],we prove that{un}converges strongly touinXλ.To this end,letϕ∈Xλbe fixed and denote byBϕthe linear functional onXλde fined by for allv∈Xλ.By the Hlder inequality and de finition ofBϕ,we have To prove our main result,we will use the Krasnoselskii’s genus introduced by Krasnoselskii in[38].LetXbe a Banach space and let us denote by Λ the class of all closed subsetsA⊂X{0}that are symmetric with respect to the origin;that is,u∈Aimplies−u∈A. Theorem 2.6(See[28])LetXbe an in finite dimensional Banach space and letJ∈C1(X,R)be even functional withJ(0)=0.IfX=Y⊕Z,whereYis finite dimensional andJsatisfiesthat (I1)There exist constantsρ,α>0 such thatJ(u)≥αfor allu∈∂Bρ(0)∩Z; (I2)There exists Θ>0 such thatJsatis fies the(PS)ccondition for 0 whereγ(V)is Krasnoselskii’s genus ofV.Forj∈N,set So,0≤cj≤cj+1forj>kandcj<Θ,then we get thatcjis the critical value ofJ.Furthermore,ifcj=cj+1=···=cj+m=c<Θ forj>k,thenγ(Kc)≥m+1,where Proof of Theorem 1.1We shall apply Theorem 2.6 toJλ,V.We know thatXλis a Banach space andJλ,V∈C1(Xλ,R).By(2.8),functionalJλ,Vsatis fiesJλ,V(0)=0.We divide the proof into the following four steps: Step 1We will show thatJλ,Vsatis fies Hypothesis(I1).By(2.7),foru∈Xλ,we have Step2We will sho wthatJλ,Vsatisfies Hypothesis(I3).Letis finite dimensional subspace ofXλ.Because all the norm in the finite dimensional space are equivalent,then for anyu∈,one can get for some positive constantC0>0.Also,sp Step 3We will prove that there exists a sequence{Υn}⊂(0,+∞)with Υn≤Υn+1,such that To this end,in view of the de finition ofcn,one can get so by the de finiti on of Γn,we get Υn<+∞and Υn≤Υn+1. Step 4We will prove that problem(1.1)has at leastkpair of weak solutions.To this e nd,using the similar argument in the proof of Theorem 1 in[31],fork≥1,by choosing.So,by Step 3,one can get Hence,by Theorem 2.6 and Proposition 9.30 in[28],the levelc1≤c2≤···≤ckare critical values ofJλ,V.Ifcj=cj+1,then by Theorem 2.6 and Remark 2.12 in[1],Kcjcontains in finitely many distinct points and therefore problem(1.1)has in finitely many weak solutions.Therefore,problem(1.1)has at leastkpair of weak solutions.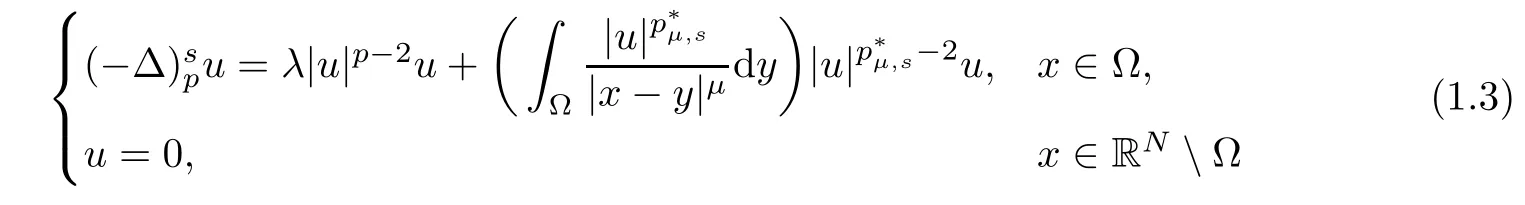
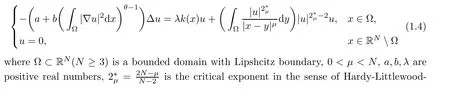

2 Preliminary Lemmas

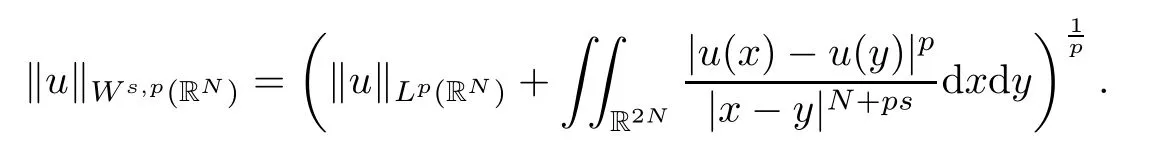

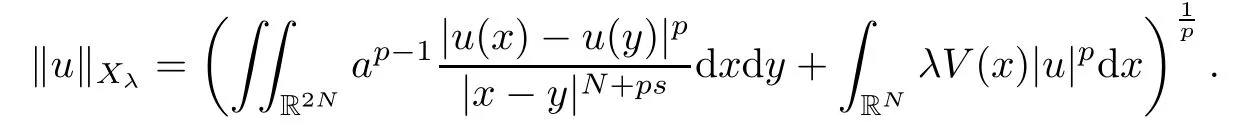
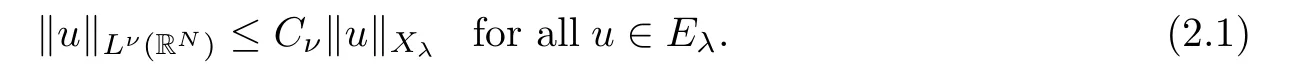

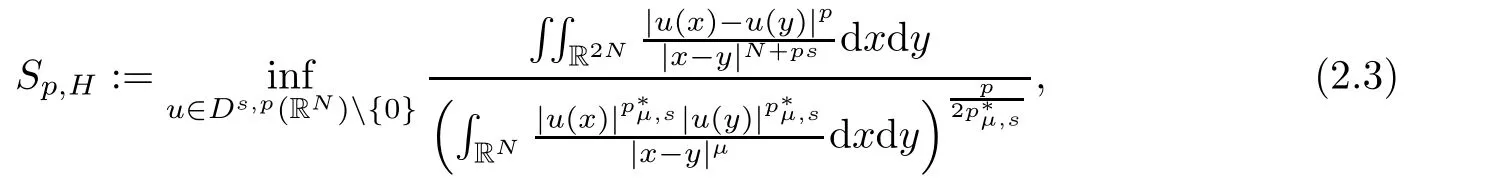

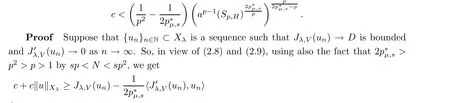
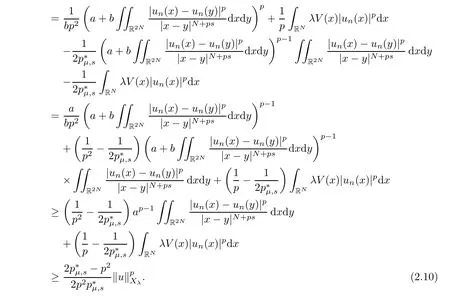



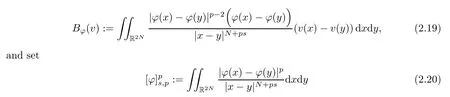



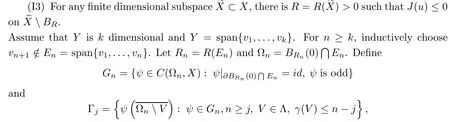


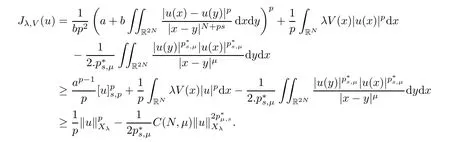

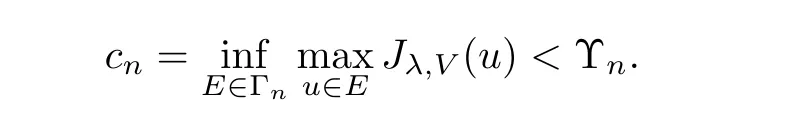
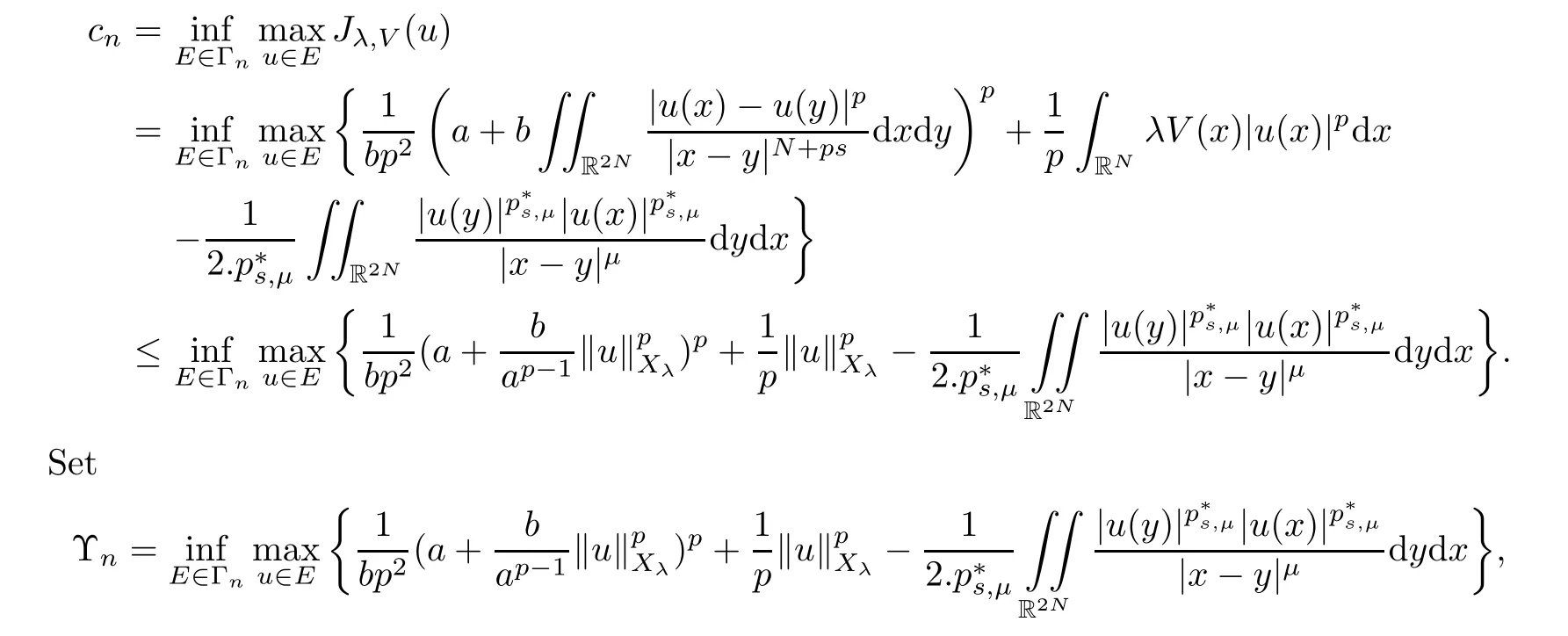
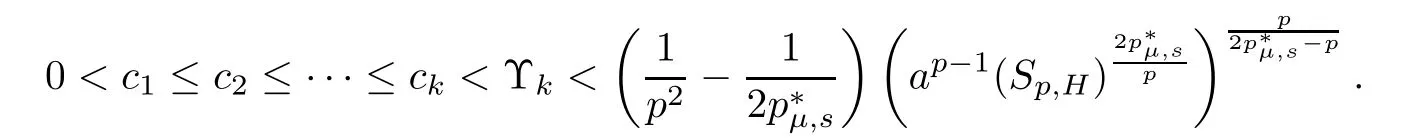
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY OF WEAK SOLUTIONS TO A CLASS OF NONLINEAR PROBLEM∗
- A DIFFUSIVE SVEIR EPIDEMIC MODEL WITH TIME DELAY AND GENERAL INCIDENCE∗
- ON A COUPLED INTEGRO-DIFFERENTIAL SYSTEM INVOLVING MIXED FRACTIONAL DERIVATIVES AND INTEGRALS OF DIFFERENT ORDERS∗
- CLASSIFICATION OF SOLUTIONS TO HIGHER FRACTIONAL ORDER SYSTEMS∗
- ENERGY CONSERVATION FOR SOLUTIONS OF INCOMPRESSIBLE VISCOELASTIC FLUIDS∗
- JULIA LIMITING DIRECTIONS OF ENTIRE SOLUTIONS OF COMPLEX DIFFERENTIAL EQUATIONS∗
