基于突变理论的岩溶隧道拱顶安全厚度分析与失稳预测

2021-11-13邹洋彭立敏张智勇雷明锋彭龙施成华

铁道科学与工程学报 2021年10期

邹洋，彭立敏，张智勇，雷明锋，彭龙，施成华

(1.中南大学土木工程学院，湖南长沙 410075；2.中交三航局第三工程有限公司，江苏南京 210011)

我国幅员辽阔，地理地质条件十分复杂，是世界岩溶分布最广的国家，特别是贵州、广西及云南等西南部地区。随着国家“西部大开发”的全面推进，各类诸如高速公路、铁路等基础设施不断向西部延伸，必将跨越广大岩溶地区[1]。已有实践表明，岩溶隧道施工受溶洞、溶腔内充满填充物以及突水突泥等影响显著。其中，隧道与溶洞间岩层的失稳、垮塌是岩溶区隧道常见的工程问题之一，严重地影响隧道施工和运营安全。因此，研究岩溶区隧道与溶洞间的安全厚度，确保两者间岩层的稳定性对保证岩溶区隧道施工及运营期的安全具有重要的现实意义[2−3]。针对岩溶隧道岩墙安全厚度及失稳问题，大量学者通过经验类比、数值模拟和理论计算等方法开展了研究。在经验类比方面，林杭等[4]利用强度折减法，建立了岩体厚度折减法理论；刘超群等[5]基于工程经验，对不同因素进行回归统计，确立了岩墙安全厚度的经验公式。在数值模拟方面，曹茜[6]以宜万铁路为工程依托，采用FLAC3D对岩溶隧道洞壁安全距离开展模拟，建立了数学预测模型。刘晓蕾[7]利用Midas软件分析了溶洞的大小与分布对隧道围岩稳定性的影响。在理论研究方面，周科平等[8]利用非线性原理中的BP人工神经网络方法，建立了安全厚度预测模型；王勇等[9]采用回归方式建立隧道与溶洞的安全厚度模型；赖永标[10]采用支持向量机技术建立了溶洞塌陷的预测模型；宋战平等[11]根据岩体抗拉、抗剪强度准则，应用弹性梁、板理论建立了隧道底板安全厚度的计算方法。杨子汉等[12]基于极限分析上限原理，提出了2种不同准则下岩土厚度的计算方法。郭佳奇等[13]基于塑性区贯通理论，得到了岩柱稳定性的判断标准，建立了中间岩柱安全厚度的力学预测模型。总体而言，经验类比法取值较为保守，而且由于地下工程的地质条件大多不同，难以精确类比；数值模拟能考虑诸多因素的影响，但计算结果的准确性需要实践验证，无法单独作为判断依据；而前述理论计算方法可以提供较好依据，但选取的参数繁多复杂，且很多参数难以测量，在实际工程中应用有限。近年来，突变理论在解决岩土工程的稳定性问题中运用广泛。该理论通过总势能原理，求得临界破坏条件，从而判定结构是否稳定。QIN等[14]采用尖点突变理论研究了边坡的滑移失稳现象，建立了其失稳判据；JIANG等[15]基于尖点突变模型，研究了岩溶地区路基溶洞顶板安全厚度计算方法，推导了路基洞室的失稳必要条件；姜德义等[16]采用固支大变形圆板突变模型研究了单井溶腔顶板的稳定性，确立了溶腔顶板失稳的临界条件；付成华等[17]应用突变理论，建立了5种地下工程洞室围岩失稳判据；师海等[2]基于弹性梁与弹性圆板模型，确立了溶洞与掌子面不同空间状态下的安全距离计算公式；YANG等[3]通过改进的椭圆板模型和固支梁模型，充分考虑地下水的影响，推导了隧道底板临界安全厚度的表达式；进一步通过极限分析方法和突变理论研究了围岩中隧道底板的坍塌形态与失稳条件[18]。综合上述分析可见，目前基于突变理论的岩溶隧道安全厚度的研究，主要集中在简化的弹性梁、板模型上，大多将自身重力简化成均布面力，事实上，重力是一个与岩梁厚度有关的体力，而将其按体力考虑的隧道拱顶失稳预测模型尚未见到报道。为此，本文在上述成果的基础上，采用突变理论分析方法，综合考虑重力、坡度等因素，针对岩溶隧道顶板的安全厚度及拱顶失稳的预测方法开展进一步研究。

1 基于突变理论的分析模型

岩溶隧道与溶洞间岩层在外力作用下发生失稳坍塌，可以认为是一种弹性能量的聚集——瞬间释放的过程[2]，其临界状态必定对应着隧道拱顶位移的临界值。当拱顶变形超过此临界位移时，岩体将会失稳而直至坍塌，此时隧道与溶洞间岩层的厚度即为岩溶隧道顶板的临界安全厚度。因此，可以通过用现代非线性的突变理论来分析拱顶溶洞与隧道间安全距离，进而预测其失稳状态。

1.1 突变理论

突变理论是非线性科学的一个分支，突变理论是法国数学家RENE Thom(1972)提出的，旨在研究自然界中跳跃性变化现象的一种数学方法。该方法的基本思想是通过系统中建立各种形式的微分方程，在相应变量影响下，预测系统的状态。目前尖点突变模型是岩溶地区工程问题分析中应用最广泛的一种[19]。

尖点突变模型是由ZEEMAN提出来的，其势函数的标准形式为[10]：

式中：x为状态变量；u和v是控制变量。

根据势能函数，可求得S集在控制平面上的投影为分叉集B(如图1)，故而分叉集B满足：

图1 尖点突变模型示意图Fig.1 Cusp catastrophe model sketch map

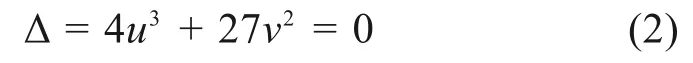
由式(2)可知，只有u≤0才有跨越分叉集的可能，故系统发生突跳的必要条件为：

当控制变量u和v同时满足方程式(2)和式(3)时，系统处于临界状态。

1.2 岩溶隧道顶板力学模型

当采用尖点突变理论建立势函数及其分支集方程，需要构建合适的力学模型。文献[3]和[15]将隧道与溶洞间岩层看作椭圆板或固支梁进行分析，但其均将岩板的重力简化为一个均布面荷载，且未考虑隧道坡度的影响，故需要作出一定的修改，建立如图2所示的岩溶隧道顶板力学模型。根据工程经验及前人研究成果，该模型简化和假定如下：

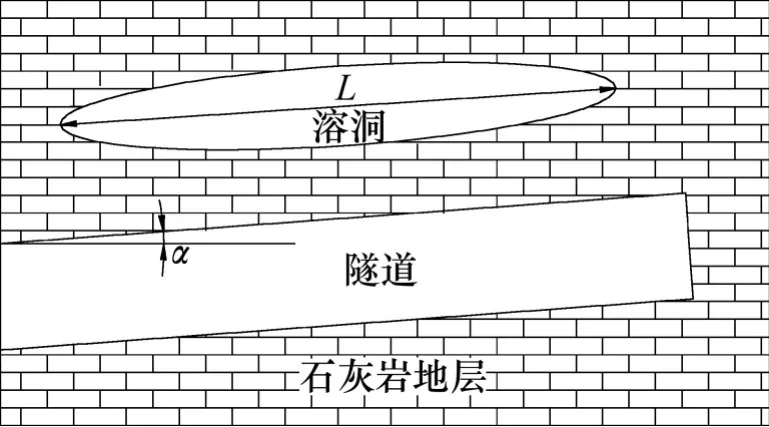
图2 岩溶隧道的结构示意图Fig.2 Structure of tunnel proof in karst region

1)隧道顶板岩体体系结构保持完整，无裂隙或缺陷，隧道与溶洞呈平行状态。

2)隧道顶板力学模型视为两端固支的均质梁，将岩梁两端的地质构造应力简化为轴向力。

3)溶洞水对隧道顶板岩层的作用仅体现为水压力，忽略其对围岩参数弱化作用。

简化的力学模型如图3所示，洞顶跨度为L，水平宽度为单位长度，厚度为H，岩石弹性模量为E，自重为q，溶腔压力简化为均布荷载p，以及岩梁两端轴向力N，隧道施工坡度为α。

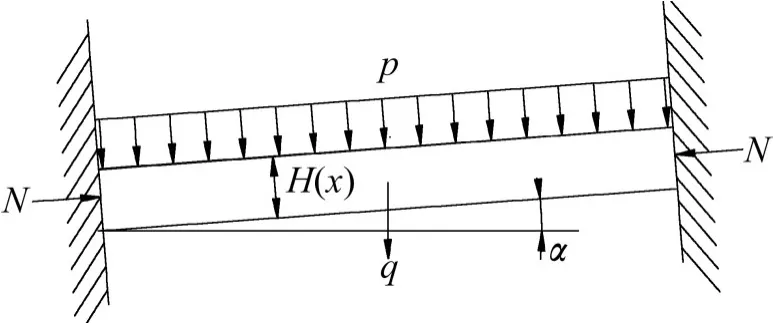
图3 隧道顶板力学模型Fig.3 Mechanical model of clamped beam

2 岩溶隧道顶板安全厚度计算

岩石弯曲变形的过程是外力能量积累的过程，当弹性能增加到一个临界值时，隧道发生失稳破坏。因此，首先应求出该力学模型系统的总势能，构建势函数表达式，并将其变换为尖点突变模型的标准数学表达式，进而求得隧道顶板安全厚度。

2.1 构建势能函数

针对图3所示的简化力学模型，由弹性稳定理论可知，系统的总势能V(x)为梁的应变能改变量，即弯曲应变能、势能和外力做功改变量的负值之和[3]：

式中：V1，V2分别为弯曲应变能、系统增加的势能；V3，V4分别为重力与水压力、轴向构造力做的功。

由基本的力学分析可知，岩梁的挠曲线方程为：

式中：w为岩梁中点挠度；x为到岩梁端部的距离。进而，由弹性力学可知岩梁的弯曲应变能为：

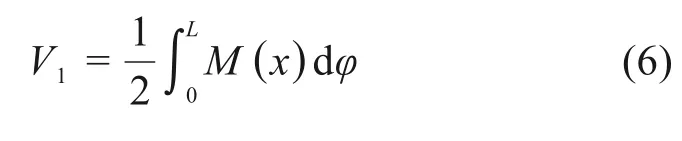
式中：M(x)为岩梁在x处的弯矩；dφ为梁挠曲线切线变化的角度，其表达式为：

式中：E为岩梁的弹性模量；I为岩梁的惯性矩；y′，y″分别是u(x)的1阶和2阶导数。

因此，将ds进行泰勒展开，忽略高阶量无穷小量，并将式(7)代入式(6)，有：

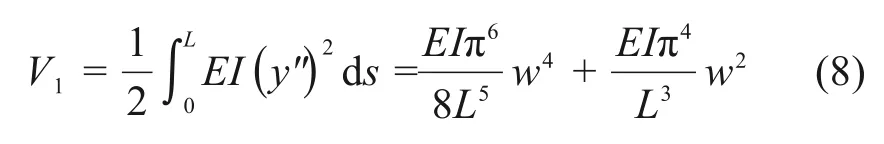
同理可分别得到系统势能的增加量、重力及溶腔水压力、轴向构造力做的功分别为[5]：

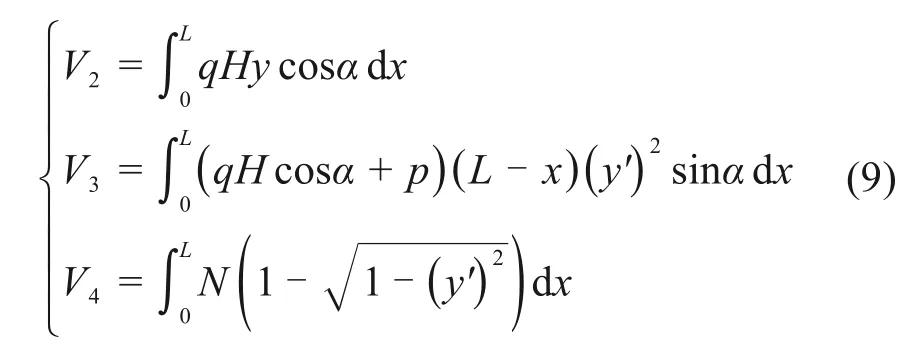
则将式(8)和式(9)代入式(4)中并计算可得势函数的表达式为：

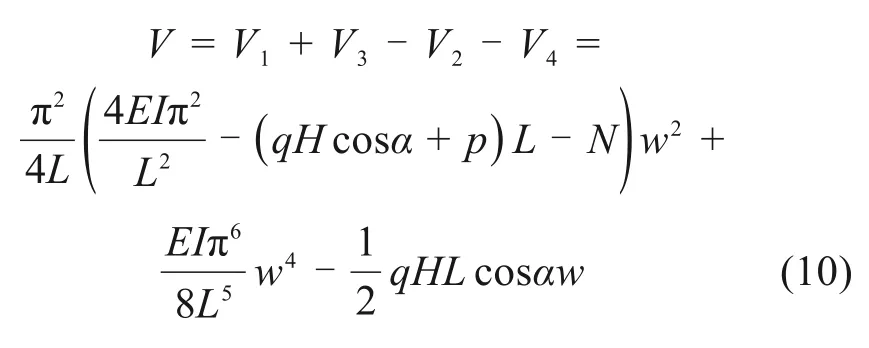
2.2 临界安全厚度

基于尖点变理论，令势函数表达式(10)中：

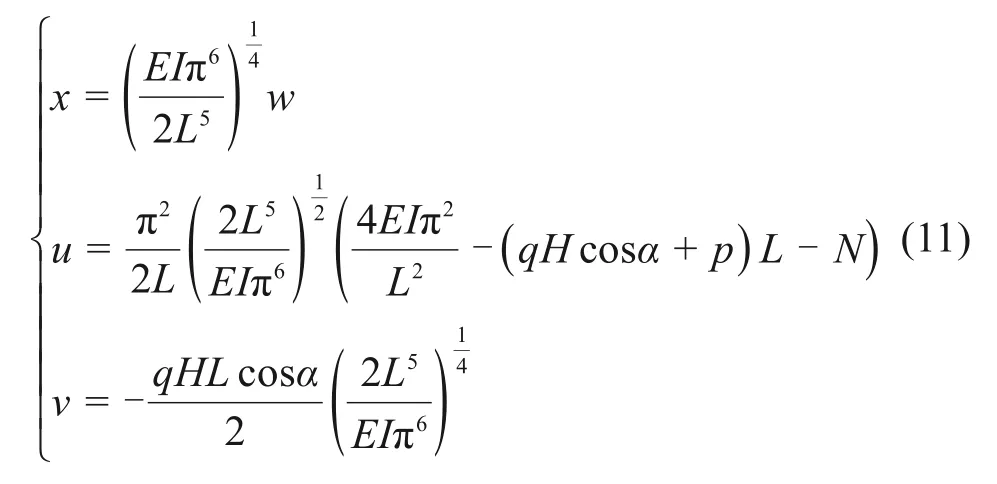
于是，可得出岩隧道顶板模型势函数的标准形式和叉分集方程为：

由前述突变理论可知，当控制变量u和v满足分叉集方程式(12)时，岩溶隧道系统发生临界突变失稳，即：

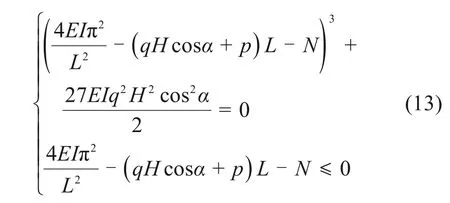
在实际工程应用中，当隧道为非超埋隧道时，N取值不大，因此，可认为构造力N对势函数的影响不大，于是可对模型再一步进行简化，可得岩溶隧道系统发生突变失稳的临界条件为：

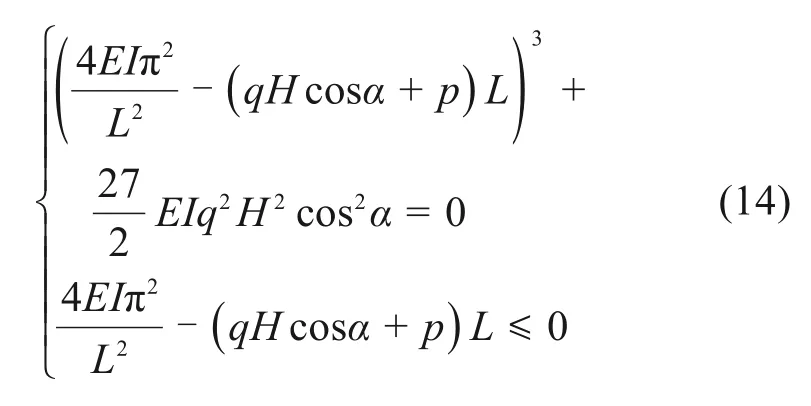
式中：顶板岩梁的惯性矩I=H3/12。

当忽略构造力N时，进一步计算发现式(13)和式(14)的结果相差不大[3]，因此，可将岩溶隧道顶板临界安全厚度进一步简化为：

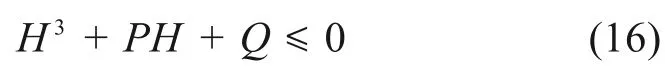
于是，得到临界安全厚度为：

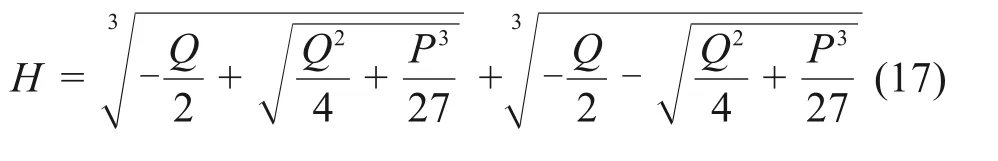
3 参数影响分析

根据上述推导过程可知，基于尖点突变理论的岩溶隧道顶板安全厚度受到顶板跨度、岩石弹性模量、自重、溶腔压力以及隧道施工的坡度等多个参数的影响，典型取值范围下，各因素对应的影响规律计算结果如图4。从中分析可知：

1)溶洞跨度在2～12 m，临界安全厚度都与溶洞跨度有着明显的正相关关系，如图4(a)。

2)溶腔压力从0.2 MPa增加到1.2 MPa时，对应的顶板安全厚度也逐步增大，尤其溶洞跨度较大时，临界安全厚度增大显著，如图4(b)。

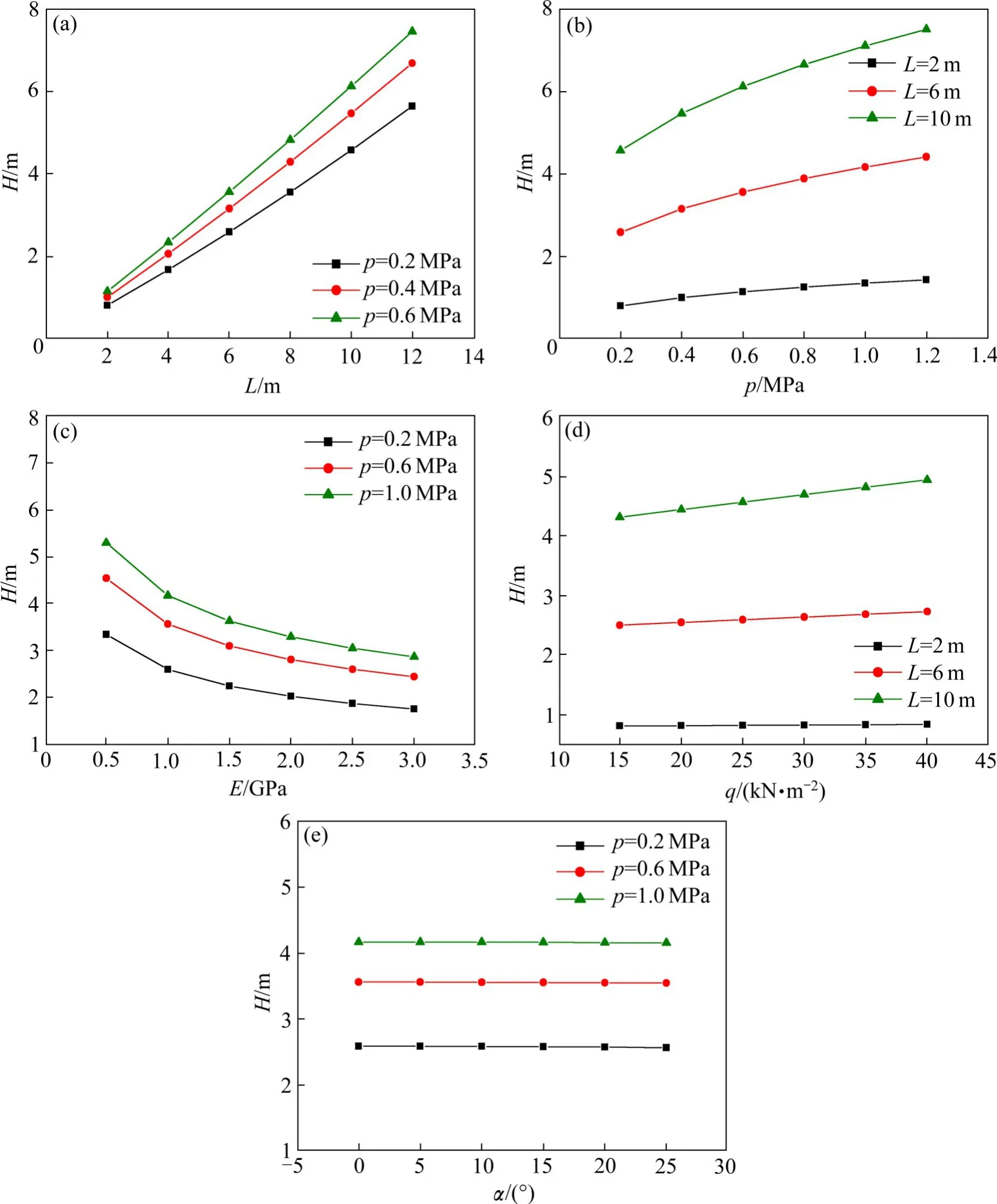
图4 相关因素对安全厚度的影响规律Fig.4 Relationship of safety thickness and factors

3)当围岩弹模0.2～1.2 GPa时，顶板临界安全厚度均随着溶腔压力的增加而减少，而在实际中弹模为1 GPa左右的区间，临界安全厚度受弹模的影响较大，说明实际工程中，围岩力学参数性质的下降，对隧道拱顶的稳定性影响很大，如图4(c)。

4)围岩重度取值为15～40 kN/m3时，当溶洞跨距较小时，对顶板安全厚度基本无影响，但较大时，顶板安全厚度与围岩重度显现出正相关关系，不过总体围岩重度对安全厚度的影响不大，如图4(d)。

5)隧道坡度取值为0~25°时，隧道坡度对顶板安全厚度基本没有太大的影响。其原因在于隧道坡度仅能通过改变重力与岩梁间的方向对安全厚度产生影响，如图4(e)。

综上所述，溶洞的跨度对岩溶隧道顶板安全厚度影响最大，其次围岩弹模，再者是溶腔水压力。说明在实际岩溶隧道中，大溶洞，围岩性质较差，溶洞水压力大的时候，隧道顶板容易发生失稳。

4 实例分析

为更进一步验证计算结果的正确性，确保隧道建设的安全，以沪昆客运专线斗磨隧道[2]和宜万线鲁竹坝隧道岩溶段[6]为例进行应用分析。

1)斗磨隧道

斗磨隧道施工过程中，在里程DK842+736～+765处发育有一较大的溶腔，富水，其间夹泥较重，经测定水压约为0.37～0.42 MPa，围岩容重为25 kN/m3，弹性模量为1 GPa，隧道溶洞之间的岩梁长度为13 m，隧道坡度为0，经过实际测量，隧道与隐伏溶洞间的距离为5～6 m。在实际工程开挖过程中，隧道岩梁拱顶沉降较大，存在失稳迹象，故而对富水溶腔采用帷幕注浆进行加固处理

2)鲁竹坝隧道

据该隧道物探资料可知，在隧道里程DK205+170处岩溶发育，施工中可能发生灾害性的突泥、塌陷。对溶腔放水，水压稳定在0.2 MPa，围岩容重为23 kN/m3，弹性模量为0.9 GPa，隧道溶洞之间的岩梁长度为8 m，隧道坡度为0。实际揭露隧道与隐伏溶洞间的距离约为3.6 m，未产生失稳现象。

将这2个实际工程案例分别代入文献[3]与本文推导的计算公式，计算结果如表1。

表1 工程实例对比Table 1 Comparision of tunnel case calculated by different approaches and the measured data

从中分析可知，在斗磨隧道的参数条件下，实际岩板厚度均小于2种计算方法计算得出的临界安全厚度，预测隧道发生失稳，与实际稳合，但本文计算的安全厚度值更接近实际厚度。而在鲁竹坝隧道的工程情况下，文献[3]计算得出的临界安全厚度大于实际岩板厚度，预测隧道发生失稳，然而实际隧道并未发生失稳；本文计算的结果下，隧道不会发生失稳，与工程实际一致。

综上所述，本文计算方法中虽然围岩重度对安全全厚度的直接影响较小。在与其他文献对比分析中，明显可以得到，加入安全厚度对自重的影响，相同参数情况下，本文计算的安全厚度的值要小，与实际结果更为接近，说明本文计算方法适用性更广。

5 失稳预测分析及验证

5.1 失稳预测模型

前述计算方法可以根据溶洞、围岩的实际状态判断岩溶隧道最终是否会发生失稳，但无法预测发生失稳时间，而在特定的施工条件，隧道穿越岩溶地区无法与富水溶洞保持安全距离，这时对隧道失稳时间的预测就显得尤为重要。针对隧道发生失稳的时间，可以在隧道失稳前采取相应的技术措施，以保证隧道施工的正常进行，提升隧道建设的经济性。

由于岩溶隧道拱顶失稳的过程均可认为是一种突变过程，考虑到隧道实际施工环境中围岩参数的难以准确测量，以及溶洞分布位置，大小，方向的随机性，而势函数V(x)=x4/4+ux4/2+vx实际是一个只与拱顶最大沉降有关的量，因此可结合隧道拱顶的实际监测数据分析一般岩溶隧道拱顶的安全性。

将拱顶下沉变形当作状态变量G[17]，状态变量随时间变化的函数采用式(18)表示：

式中：t为隧道开挖日期到变形观测日期的累计天数。

将函数进行Taylor级数展开，取对函数影响显著的前4次项，可得：

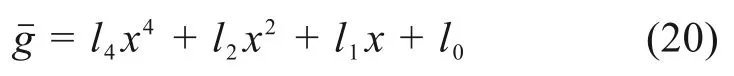
式(20)中：l0为一不影响系统突变的常量，因此可将状态变量G化为尖点突变理论的标准形式：

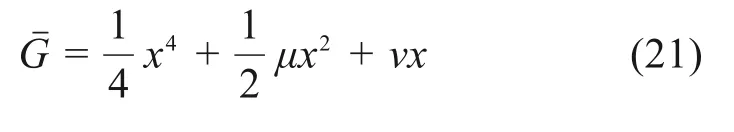
式中：μ=l2/2l4，v=l1/4l4。

同理，由尖点突变的基本理论[19]，可得到系统的平衡方程为：

系统发生不稳定突变的状态标准为:

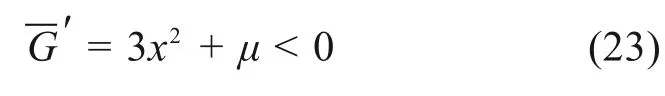
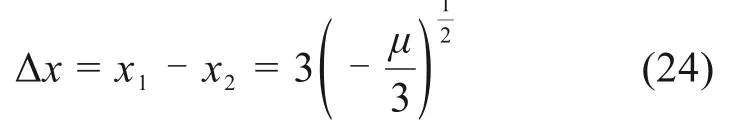
进而，可求得隧道围岩的失稳时间：

5.2 模型的验证

以房十房高速公路某隧道为例，结合工程实际情况和现场实测数据，建立隧道拱顶塌方的失稳预测模型，预测隧道拱顶塌方的时间，并对所建立的尖点突变预测模型进行检验。

图5给出了该隧道拱顶实测沉降时程曲线。通过回归分析，可得到该隧道的拱顶沉降时程函数：

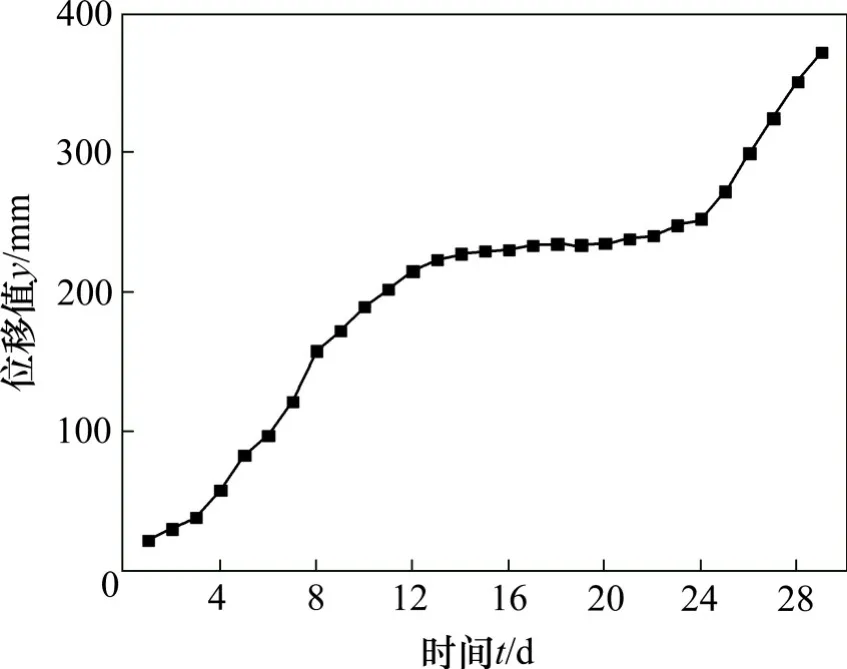
图5 隧道拱顶监测点累计沉降曲线Fig.5 Monitoring cumulative settlement curve of tunnel vault

将拟合得到的参数代入式(20)，可得：

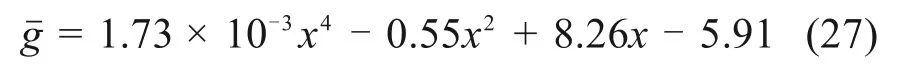
进一步按式(21)标准化可得到：μ=-15.98，v=1 192.20，并将所有参数代入式(24)和式(25)中，有t≈24 d。而实际隧道施工过程中，在施工后25 d后，隧道拱顶发生失稳。可见，该模型预测的隧道拱顶失稳时间与实际基本稳合，证实了本文推导的岩溶隧道拱顶失稳预测模型的有效性，可为此类情况下隧道的设计和施工提供指导。