考虑时间效应的黑色页岩遇水三向宏微观膨胀力模型研究

2021-11-13朱宝龙李倩王聖林陈强

铁道科学与工程学报 2021年10期

朱宝龙，李倩，王聖林，陈强

(1.西南科技大学土木工程与建筑学院，四川绵阳 621010；2.西南交通大学地球科学与环境工程学院，四川成都 611756)

黑色页岩是一类分布广泛、成分复杂的沉积岩类，由于其在表生环境下容易风化，产生了较多边坡或滑坡工程问题，引起许多学者的关注[1]。水是黑色页岩风化过程中重要因素，黑色页岩遇水后，其中的黏土矿物吸水产生膨胀，在宏观上表现为岩石崩解或脱落，导致岩体结构进一步破坏[2−3]，因此，黑色页岩遇水膨胀作用造成物理力学性质弱化是岩石风化过程中不可忽视的作用，探讨岩石遇水条件下膨胀力随时间的变化规律，建立考虑时效性的膨胀力模型，对于黑色页岩区域工程膨胀问题的解决具有一定的参考意义。关于页岩膨胀模型研究方面，较早时BRACKLEY[4]建立了一个考虑初始含水量、液限的影响和黏土组分的模型来获得建筑物下土壤膨胀时的最大膨胀量。EROL等[5]使用倍数与非线性回归分析进行了建模预测页岩的自由溶胀潜力。SABTAN[6]开发了一个包含塑性指数、初始含水量和黏粒组分参数的多元线性回归模型来估计30个未扰动页岩样品的膨胀体积。GOMEZ-GUTIERREZ等[7]对未风化页岩进行了沉降耐久性和膨胀试验，提出了包含耐久性指数、黏粒组分等参数的膨胀体积预测方程。孙仁远等[8]提出了一种关于描述页岩膨胀率与黏土含量、压力、温度定量关系的Log-Normal拟合模型。范秋雁等[9−10]针对膨胀岩提出了多种工况下的膨胀率时程模型。但上述所提出的膨胀模型大多集中考虑页岩或膨胀岩的膨胀变形过程，较少涉及膨胀力的变化过程。为消除过多因素的影响，有学者专门针对膨胀岩膨胀模型进行研究，以便揭示其遇水膨胀过程中的应力−应变关系。20世纪70年代，HUDER等[11]提出了关于轴向应变与膨胀压力的对数呈线性关系的Huder-Amberg膨胀本构模型；此后，EINSTEIN等[12−13]在此基础上进行改进，将一维情况推广至三维膨胀本构模型；为进一步考虑膨胀过程中的时间因素，刘晓丽等[14−15]推导了结合时间因素的三维膨胀本构关系。这些学者提出的一维或三维膨胀本构模型主要是从宏观角度来描述岩石膨胀量或膨胀力，较少涉及微观层面，但对于页岩或膨胀岩来说，内在的微观机制是产生宏观膨胀效应的主导因素[3]，因此，进一步从微观层次来探讨页岩或膨胀岩结合时间因素的膨胀力模型具有一定的内在机理准确性。本文选择黑色页岩为研究对象，在宏观三向膨胀力试验基础上，从微观角度考虑黏土矿物的膨胀机制，基于双电层理论[16]建立其三向膨胀力本构模型，对于岩石膨胀机理的研究具有一定的补充意义。

1 黑色页岩基本物理力学性质

本次试验所用黑色页岩取自重庆市武隆县江口镇下志留统龙马溪组黑色页岩地层新鲜露头。对岩石进行矿物成分分析得出，石英含量为40.01%，黏土矿物含量为37.23%(高岭石2.94%，伊利石18.89%，蒙脱石6.57%，绿泥石8.83%)，长石、白云石等其他矿物含量为22.76%。

由于黑色页岩具有典型的层理特征，如图1，考虑其各向异性[17]，按z方向取样进行基础物理力学性质试验，经多次室内试验得到相关参数典型值如表1所示(图1中的a试样)，同时为得到x，y方向的泊松比，按照相应方向取样得到相应值(图1中的c，b试样)，可以看出z方向泊松比大于x，y方向值，x，y方向虽然较为接近，但仍存在差异，体现出一定的各向异性。

图1 黑色页岩试验取样示意Fig.1 Test samples of black shale

表1 黑色页岩物理力学性质参数Table 1 Physical and mechanical properties of black shale

2 黏土矿物晶层间距测试

将野外取回的黑色页岩大块试样切割成1 cm×1 cm左右的试样进行试验，置入去离子水中浸泡，在1，5，10，15，20，25，30 d浸泡时间取出3块(依次编号1～3)，研磨成岩石粉末，采用D/MAX-2500的X射线衍射仪(Cu-Ka靶辐射，Ni滤光，λ=1.540 59Å)进行分析，扫描角度为2°～80°2θ(2θ为衍射角)，扫描速度为0.02(°)2θ/s，电压为40 kV，电流为250 mA。通过X射线衍射法测试，得到黏土矿物晶层间距变化。晶面层间距计算采用Bragg公式：

式中：d为所求的001晶面间距；λ为所用靶的波长。

本次测试采用Cu-Ka靶辐射，λ=1.540 59Å；k为衍射级数，本次测试为1级衍射，取k=1。θ由衍射峰位置决定。根据式(1)，可计算蒙脱石、伊利石、绿泥石3种矿物系列原样及在浸泡1，5，10，20，30 d时的晶层间距变化(见图2)。

图2 黑色页岩中3种黏土矿物晶层间距变化Fig.2 Crystal layer spacing variation of three clay minerals in black shale

由图2(a)可知，蒙脱石随浸泡时间的增长，晶层间距不断增大，在前10 d增长较快，10 d后增长速率变缓，最终，30 d时，晶层间距增大0.9 177 nm，即增大21.832 3%。伊利石随浸泡时间的增长，晶层间距不断增大，最终，30 d时，晶层间距增大0.001 6 nm，即增大0.027 8%，从拟合曲线来看，30 d后仍有少量增大趋势，但基本趋于平稳(图2(b))。同样地，绿泥石随浸泡时间的增长，晶层间距不断增大，在前10 d增长较快，增长了约0.089 3%，10 d后仍进一步增大，但增长率较前10 d小，最终，30 d时，晶层间距增大0.008 2 nm，即增大0.116 3%(图2(c))。

3 三向膨胀力试验

试验采用改进的三向膨胀仪进行，系统由试验仓、储水箱及数据采集箱组成，可同时量测x，y，z3个方向膨胀力，如图3。

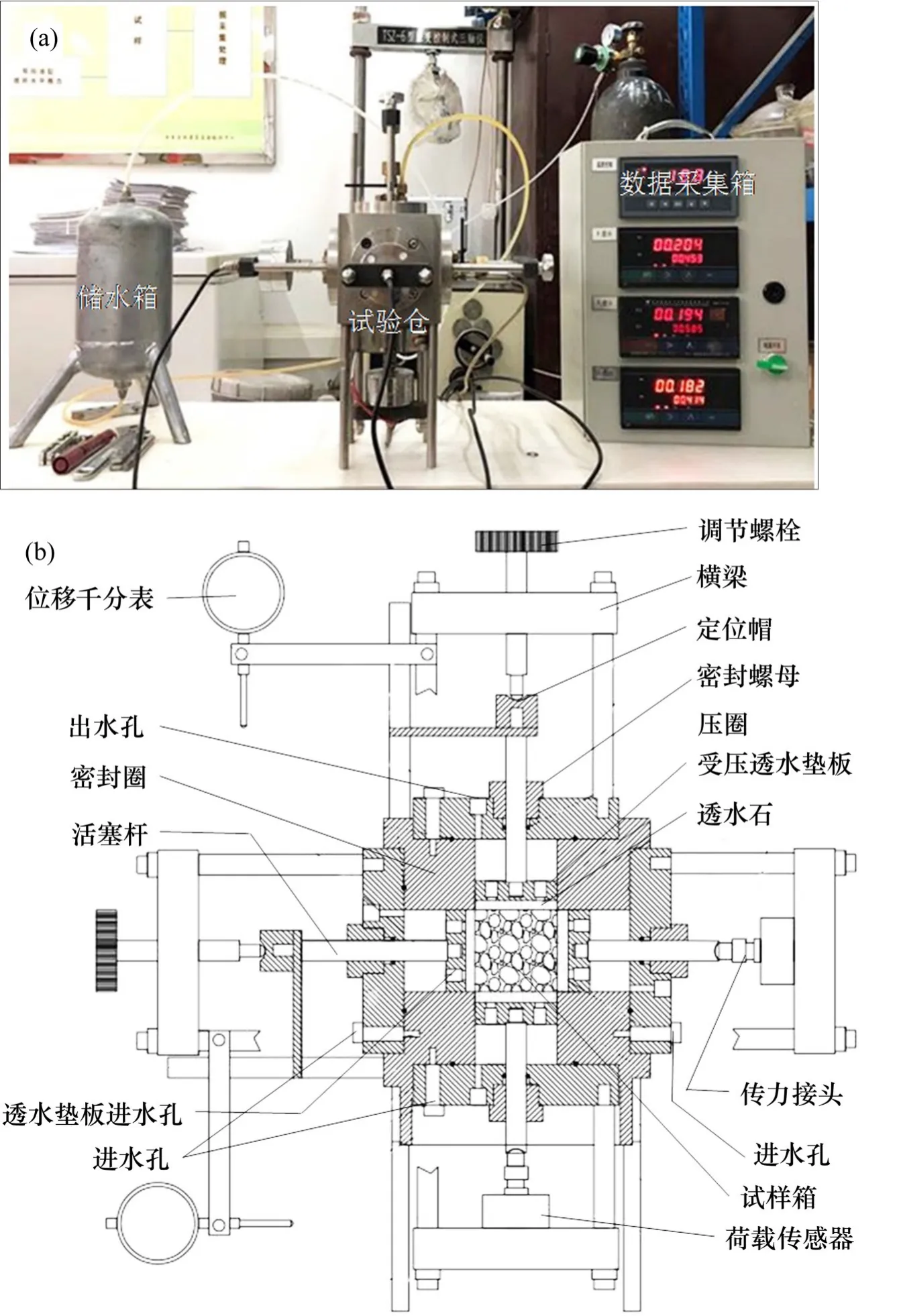
图3 三向膨胀仪Fig.3 Three dimension swelling apparatus

三向膨胀仪是以平衡压力法原理设计。处于试样箱中4 cm×4 cm×4 cm(图1中的d试样)大小的试样在水的作用下向外发生膨胀变形时，首先作用到受压透水垫板上，透水垫板将力通过活塞杆传递到荷载传感器上，测得试样在完全侧限条件下的x，y和z三向膨胀力大小。

图4为试验后试样。图5为试验得到的30 d内黑色页岩膨胀力变化曲线，可以看出，z方向的膨胀力最大，发展也最快，x方向膨胀力次之，膨胀力最小的是y方向。在蒸馏水中z，x和y方向膨胀力在初期增长显著，在8 d左右基本稳定。最终x方向、y方向的膨胀力分别为z方向膨胀力的0.306，0.287倍，表现出一定的各向异性。依据其增长速率可以将整个膨胀力发展过程分为3个阶段：

图4 三向膨胀力试验后试样Fig.4 Sample after 3D swelling test

图5 黑色页岩三向膨胀力试验时程曲线Fig.5 Experimental evolution of 3D swelling pressure of black shale

1)加速发展阶段。随着开始向岩样中注水，在0～2 d，岩样膨胀力以较快速度持续增大，z方向增长速度快于x，y方向。在z方向上此阶段膨胀力占总膨胀力的74%，x方向上占71%，y方向占88%。水在压力作用下快速进入岩样内部，并在微观层面上水进入蒙脱石等黏土矿物内部，引起晶格距离增大，从而在宏观上表现为向外产生膨胀力。

2)减速发展阶段。随着试验的继续进行，在2～8 d内，z，x，y3个方向膨胀力继续增长，但增速放缓，增长速率约为加速发展阶段的50%，其中y方向在3 d时基本趋于稳定状态。在z方向上此阶段膨胀力占总膨胀力23%，x方向上占26%，y方向占13%。在此阶段内水与黏土矿物进一步结合，仍然存在一定的膨胀发展，但在前期水与黏土矿物结合较多的基础上，膨胀力变化幅度较第一阶段小。

3)稳定发展阶段。8 d后，x，y和z3个方向膨胀力发展基本处于稳定阶段，膨胀力随时间变化曲线较为平缓。此时岩样基本处于饱和状态，膨胀力基本达到最大值。

4 黑色页岩宏微观膨胀模型

假定黑色页岩遇水膨胀过程满足以下假定：

1)岩石是连续介质；

2)不考虑化学反应过程对岩石膨胀的影响；

3)根据膨胀力试验曲线，可以认为膨胀过程遵循弹性理论；

4)不考虑矿物膨胀过程中的相互作用或影响。

根据前人关于黏土矿物研究及上述黑色页岩微观膨胀机理的分析，一般认为页岩(或膨胀岩)中主要是伊利石、蒙脱石、绿泥石等亲水性黏土矿物遇水膨胀产生宏观膨胀力，而对于本次所选用的黑色页岩中高岭石，其含量较少且膨胀力相对很小，可以忽略不计。则如图6各向异性的黑色页岩，可将z轴方向的膨胀力关系写为

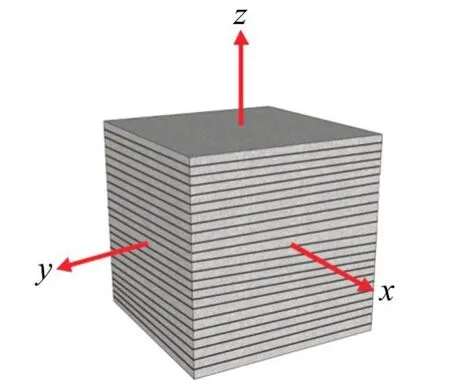
图6 黑色页岩膨胀模型Fig.6 Swelling model of black shale

式中：Sz为z轴方向的膨胀力；PI(t)为伊利石产生的膨胀力；PS(t)为蒙脱石产生的膨胀力；PC(t)为绿泥石产生的膨胀力。

按照双电层理论[18]，当岩石与水相接触时，岩石颗粒将吸附水分子，水分子进入蒙脱石颗粒扩散层，使得晶层间距变大产生膨胀。蒙脱石晶层间的相互作用力分为主要由渗透压力产生的排斥力和范德华力产生的吸引力。即蒙脱石晶层膨胀力PS(t)可写为

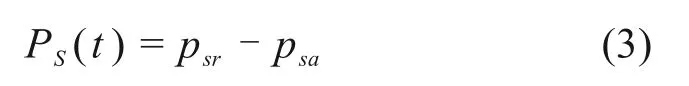
式中：psr为两相邻黏粒间的相互排斥力，kPa；psa为相互吸引力，也称为范德华力，kPa。

根据文献[18]，两晶层之间的相互排斥力psr为

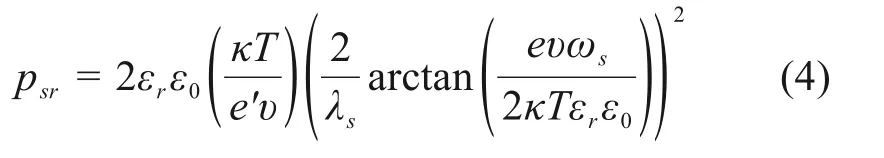
式中：ωs为晶层表面电荷密度，C/m2，可通过试验测得；ε为电容率，等于相对电容εr与真空电容率ε0之积；εr为相对电容率，80 C2/(N•m2)；ε0为真空电容率，8.854×10−12C2/(N•m2)；κ为Boltzmann常数，1.38×10−23J/K；T为绝对温度，K；e′为单位电荷，1.602×10−19C；υ为离子价，1.5；λs为蒙脱石晶层间距，m。

另外，根据文献[19]，范德华力psa的表达式为

式中：Ah为Hamaker常数；ds为蒙脱石晶层厚度，m。

则蒙脱石的膨胀力

从式(6)可以看出，其仅能计算某一时刻的蒙脱石晶层膨胀力。因此，将其中的晶层间距λs改写为

式中：t为时间，h；As，Bs，Cs为参数，可以通过试验曲线拟合得到。

易知，式(6)可改写为

式(8)即为基于双电层理论的水作用下蒙脱石膨胀力模型。

同理，可得到伊利石、绿泥石膨胀力模型。伊利石膨胀力模型：式中：λi为伊利石晶层间距，m；ωi为伊利石晶层表面电荷密度，C/m2，可通过试验测得；di为伊利石晶层厚度，m。

绿泥石膨胀力模型：

式中：λc为绿泥石晶层间距，m；ωc为绿泥石晶层表面电荷密度，C/m2，数值上等于阳离子交换量，可通过试验测得；dc为绿泥石晶层厚度，m。

则式(2)可以写为：

式(11)即为黑色页岩遇水后z方向膨胀力随时间的变化关系。

另外，在金尼克条件[5]下，因为有轴向应力σz存在，从而使得水平方向上有变形的趋势，因为将其视为连续介质，则相邻单元体间有相互作用，使得轴向应力σz产生了水平方向应力。其中，轴向σz是最大主应力，水平方向应力σx和σy为被动应力。将岩体视为空间连续性的弹性体，设水平方向尺寸不变，水平方向σx与σy相等，则

式中：μ为材料泊松比。

对于水平方向的膨胀力，采用式(12)计算时，得到x，y2个方向的膨胀力相等，考虑黑色页岩各向异性，将水平x，y方向的膨胀力定义为

式中：Kx为x方向膨胀力系数；Ky为y方向膨胀力系数；μx，μy分别为黑色页岩x，y方向的泊松比，如表1。

一般来说，蒙脱石、伊利石、绿泥石等矿物均有初始晶层间距值，可将其产生的膨胀力作为初始值，在随后矿物与水作用后晶层间距逐渐增大过程中，晶层间距变化产生的膨胀力的增量作为膨胀力在水作用下的增量。因此，可以写为

式中：SZ0为在浸水前初始晶层间距条件下初始膨胀力；ΔSZ(Δλ)为浸水后某一时刻晶层间距变化引起的膨胀力增量。则

式中：λs(0)，λi(0)，λc(0)分别为蒙脱石、伊利石、绿泥石矿物的t=0时刻初始晶层间距；Δλs(t)，Δλi(t)，Δλc(t)为蒙脱石、伊利石、绿泥石矿物某一时刻t与t=0时刻相比晶层间距的增量。

从三向膨胀力试验时程曲线(图5)可以看出，0～2 d是膨胀力初期加速发展阶段，结合黑色页岩微观膨胀机理，黑色页岩膨胀力初期主要是晶层膨胀贡献，而以上采用双电层理论进行膨胀力计算存在一定的缺陷，这也与文献[18]提出的规律一致。因此，需要对0～2 d的膨胀力模型进行修正。

对于黏土矿物膨胀，只有当晶层间距增大到某一界限值时扩散双电层才开始发挥作用，膨胀过程以黏粒扩散双电层增大为主，膨胀力变化才符合双电层理论；但晶层间距小于某界限值时，则以晶层膨胀为主。按照前述晶层间距变化测试结果，蒙脱石、伊利石、绿泥石第2 d的晶层间距分别为4.68，5.61，7.03 nm，即为其界限值。

依据文献[2]，黏土矿物中微观晶层膨胀力变化遵循式(18)

式中：Szw(t)为0～2 d的z方向膨胀力；t为时间；A，B，C为参数。

因此，综合考虑蒙脱石、伊利石、绿泥石等黏土矿物影响，结合图7试验曲线，将式(18)黑色页岩0～2 d的z方向膨胀力改写为

图7 黑色页岩三向膨胀力理论计算值与试验值对比Fig.7 Comparison of swelling pressure between theoretical and experimental values of black shale

式中：Sz0-2(t)为0～2 d的z方向膨胀力；λs，λi，λc分别为蒙脱石、伊利石、绿泥石矿物晶层间距，是时间t的函数。

将式(15)和式(19)联立，得到黑色页岩z方向膨胀力理论公式：

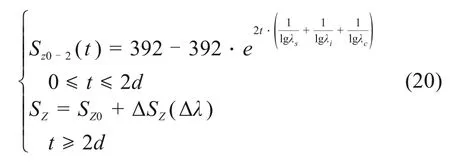
则式(20)与式(16)，(17)以及(13)，(14)构成完整的黑色页岩三向膨胀力本构关系。

根据文献[20]试验测得，蒙脱石晶层表面电荷密度0.173 C/m2，伊利石晶层表面电荷密度21.624 C/m2，绿泥石晶层表面电荷密度1.306 C/m2。

黏土矿物遇水晶层厚度变化与晶层间距变化相比相对较小，为简化起见，将晶层厚度设为定值，忽略其随时间变化对膨胀力的影响。由前文XRD测试，得到蒙脱石晶层厚度ds=0.96×10−9m及晶层间距随时间变化表达式：

伊利石晶层厚度di=0.93×10-9m及晶层间距随时间变化表达式：

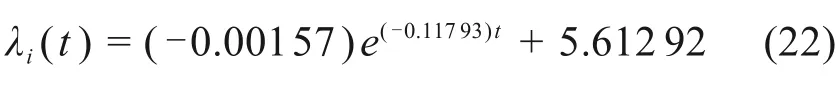
绿泥石晶层厚度dc=1.43×10-9m及晶层间距随时间变化表达式：

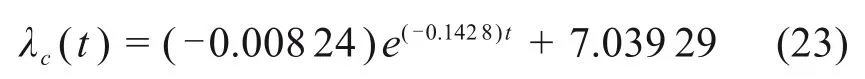
将上述测试数据及表1中数据，代入式(20)与式(16)，(17)以及(13)，(14)，得到黑色页岩三向膨胀力理论值与试验值对比如图7，膨胀力发展初期理论值增长较试验值大约3%，2 d后理论值与试验值比较接近，二者相差在1%以内。根据表1数据及金尼克条件计算得到，x方向、y方向的膨胀力分别为z方向膨胀力的0.319，0.297倍，与试验结果非常接近。理论值与试验值符合度较好，说明所提出的模型具有一定的准确性。