冻结粉细砂与钢板接触面剪切统计损伤模型构建

石泉彬，杨平

(1.南京林业大学 土木工程学院，江苏 南京 210037；2.泰州职业技术学院 建筑工程学院，江苏 泰州 225300)

冻土与结构接触面力学强度特性是人工冻结加固区盾构隧道管片合理设计、冻结施工参数正确选择、盾构机顺利推进的重要依据[1]，同时也是寒区工程设计重要依据，而深入揭示冻土与结构接触面损伤规律，尤其是构建合理的冻土与结构接触面剪切模型，则是解决此类问题的关键。冻土与结构接触面剪切模型研究通常均以不同形式的接触面剪切试验为基础，何爽等[2−7]分别开展了冻土与钢管变角剪切试验、冻结粉土与建筑物接触面直剪试验、冻砂土与铝板接触面直剪试验，杨平等[8−10]进行了冻土与结构接触面循环直剪试验，此类剪切试验虽可测出冻土与结构接触面剪切强度，但均未综合考虑接触面温度、法向应力、粗糙度等多因素耦合作用对接触面剪应力的影响。对于冻土与结构接触面剪切数值模拟，其关键在于如何构建合理的接触面单元，如贾艳敏等[11]将冻土与桩接触面处的黏结、滑移和开裂用面−面接触单元模拟，吴亚平等[12]引入桩土相互作用界面单元模拟冻土区桩土剪切作用。上述各类接触面单元均未能有效考虑冻土接触面材料内部缺陷随机性分布以及剪切残余强度对接触面剪应力的影响。统计损伤理论考虑岩土材料变形过程中损伤发生、发展的过程以及内部损伤分布的随机性，基于统计损伤理论构建的应力−应变模型，能较好反映岩土材料应变软化、硬化等特点，故在岩土工程中已有不少应用[13−15]。对于冻土与结构接触面而言，其受荷变形过程同样也是接触面损伤发生、发展的过程，其内部损伤缺陷分布亦具随机性，接触面所受应力同样由未损伤部分和损伤部分共同承担。因此，可用统计损伤力学理论对冻土与结构接触面模型进行接触面剪切强度研究。因冻土与结构接触面剪切强度受接触面冻结温度影响显著，故统计损伤模型构建须耦合与接触面剪切强度密切相关的冻结温度、粗糙度、法向应力等多种主要影响因素。

1 试验及接触面剪切变形特性分析

为构建冻土与结构接触面模型，利用改进后的大型多功能冻土直剪仪进行不同冻结温度、不同法向应力、不同粗糙度工况条件下冻土与结构接触面冻结强度直剪试验，有关该冻土直剪仪构造原理、试验参数及试验方法等见文献[16−20]。

选取南京市河西地区地铁施工区域典型粉细砂(宁和城际轨道交通天保路站：②-3d3+4及②-4d2层)为试验土样，设计含水率27%，其主要物理力学性能指标见表1，其粒径分布曲线如图1所示。

图1 粉细砂粒径分布曲线Fig.1 Particle size distribution curve of silty fine sand

表1 粉细砂物理力学特性Table 1 Physical and mechanical properties of silty fine sand

采用不同深度凹槽的剪切钢板模拟不同粗糙度结构物接触面，定义接触面粗糙度值为剪切钢板凹槽间梯形锯齿高度值[17]，其尺寸单位以mm计。粉细砂装样后先与钢板接触，土样表面在剪切板法向荷载作用下形成凹痕，后与剪切板一起冻结。剪切钢板断面及实物如图2所示。冻土与结构接触面剪切强度受剪切速率影响较小，当剪切速率较小时其随剪切速率增加而增大，剪切速率至7 mm/min其值渐趋平稳[19]。鉴于研究接触面剪切强度上限值对于工程实际更具指导和应用价值，故据此确定剪切速率7 mm/min，试验数据采集频率为1次/s。

图2 剪切钢板断面及实物图Fig.2 Sectional view and physical image of steel shear plate

剪切板下表面长度比冻结粉细砂试样上表面长40 mm(如图3)，当单程直剪行程达到最大值11 mm时，冻结粉细砂试样与剪切板的接触范围仍未超过剪切板边界，也即剪切面积始终等于冻结粉细砂试样上表面积。由于剪切面积和法向荷载均恒定不变，故剪切过程中保持接触面法向应力恒定。

图3 冻土盒及剪切板实物图Fig.3 Pysical image of frozen soil box and steel shear plate

规划设计三因素四水平试验，即：接触面法向应力σ(100，300，500和700 kPa)，剪切板粗糙度R(0，0.3，0.8和1.4 mm)，接触面温度T(−2，−6，−10和14℃)，且每组安排不少于3次平行试验。通过试验发现：在不同影响因素条件下，接触面剪切变形过程与接触面温度、粗糙度及法向应力大小相关，且呈现线弹性、应变硬化、应变软化、残余强度4个典型变化阶段，冻土与结构接触面剪切过程中极限剪切强度和残余剪切强度均受接触面温度T，粗糙度R和法向应力σ显著影响。因此，在构建冻土与结构接触面剪切模型时，应考虑到冻土区别于常温土，其接触面剪切强度除与接触面法向应力σ和粗糙度R有关外，还受接触面冻结温度T显著影响。

2 冻土接触面损伤定义及基本假定

2.1 冻土接触面损伤定义

通过对冻土与结构接触面剪切单元进行微观受力分析，将冻土接触面材料抽象为未损伤和损伤2部分，两者间截面积关系如式(1)所示。

式中：A为冻土接触面剪切单元的总截面积；A0为冻土接触面剪切单元未损伤部分的截面积；A1为冻土接触面剪切单元损伤部分的截面积。

对冻土接触面材料的损伤程度进行定义，其最为关键的是如何有效判定冻土接触面材料的损伤程度。基于统计损伤理论，接触面材料在剪切荷载作用下的损伤程度，可以通过专门的损伤因子进行描述，如式(2)所示。

式中：D为损伤因子。

2.2 模型基本假定

为构建能够反映冻土与结构接触面剪切变形全过程和剪切变形特征的统计损伤模型，依据统计损伤理论，作如下基本假定：

1)冻土与结构接触面温度、剪应力及法向应力沿接触面均匀分布，接触面粗糙度均匀分布；

2)冻土与结构接触面材料所受剪切力由未损伤和损伤2部分材料共同承担；

3)未损伤部分接触面冻土体所受到的切向微观剪应力τ′遵循线弹性法则；

4)损伤部分材料所受到的切向微观剪应力τ″等于冻土与结构接触面残余剪切强度；

5)未损伤部分所受到的法向微观正应力σ′n，损伤部分材料所受到的法向微观正应力都等于冻土与结构接触面上的法向应力σ。

在冻结粉细砂与钢板剪切过程中伴随剪胀现象和接触面凹痕作用，剪切板会因此上抬而产生竖向位移，其竖向位移与水平位移对比如图4[16]所示。

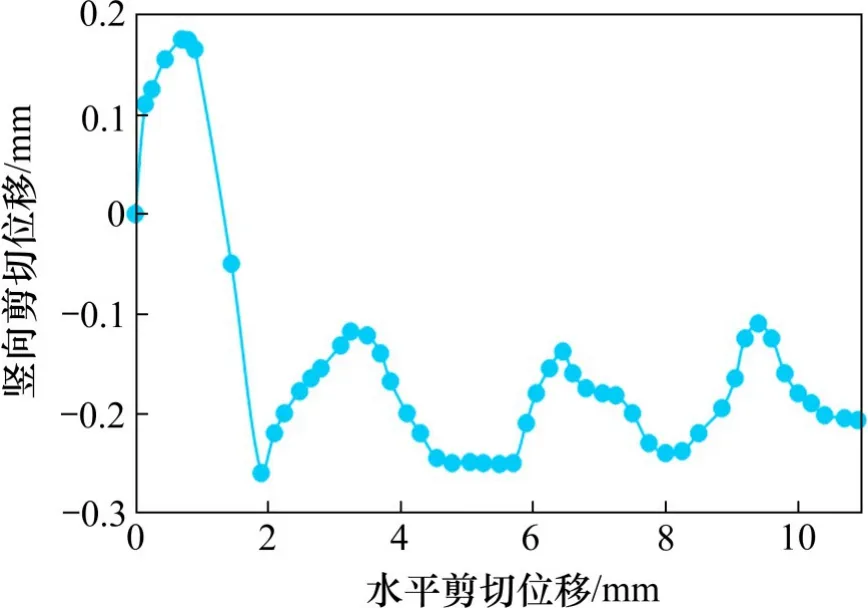
图4 直剪试验中竖向位移与水平位移的对比曲线Fig.4 Curve of vertical displacement versus horizontal displacement in direct shear test

本文剪切模型依据冻结粉细砂与剪切板接触面切线方向静力平衡条件构建，而非按能量守恒条件推导，故不考虑伴随剪胀现象上抬消耗的功。

基于上述基本假定，可以推导出式(3)～(6)：

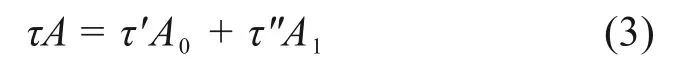
式中：τ为冻土与结构接触面剪应力；τ′为冻土接触面未损伤部分承担的微观剪应力；τ″为冻土接触面损伤部分承担的微观剪应力。

式中：kt为不同接触面温度条件下冻土与接触面剪切刚度；μ′为未损伤部分相对剪切位移。

式中：τ′r为冻土与结构接触面残余剪切强度。

3 接触面剪切统计损伤模型构建

在参考常温土接触面剪切统计损伤模型[14]构建思路的基础上，考虑冻土有别于常温岩土材料，其接触面剪切强度不仅与接触面法向正应力、粗糙度有关，还与接触面冻结温度显著相关。因此，冻土与结构接触面剪切本构模型的构建必须综合考虑接触面冻结温度、粗糙度、法向应力等多因素的耦合作用。

3.1 接触面剪切静力平衡方程建立

根据接触面剪切单元切向受力平衡关系，同时依据式(1)和式(2)有关损伤因子定义，得到冻土与结构接触面剪应力表达式，如式(7)所示。

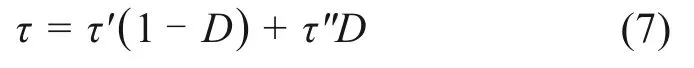
依据统计损伤理论，因冻土与结构接触面单元破坏是随机性的，故其损伤出现的位置也应当具有随机性。依据变形协调概念，未损伤部分和损伤部分的相对剪切位移一致，且冻土与结构接触面单元总体剪切位移相等，如式(8)所示。

式中：μ为冻土与结构接触面单元总体剪切位移。

将式(8)代入式(4)可以得到未损伤部分材料的剪应力，如式(9)所示。

式中：kt为不同接触面温度条件下冻土与结构接触面剪切刚度，是接触面温度的函数，可由冻土与结构接触面直剪试验剪应力−剪切位移关系曲线求得。

将式(9)代入式(7)得冻土与结构接触面剪切静力平衡方程，也即接触面剪切损伤模型，如式(10)。当接触面材料受外荷载作用后处于完全损伤状态，即D=1时，τ=。

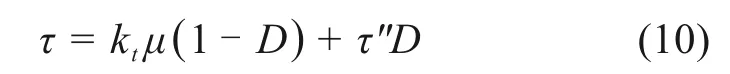
3.2 接触面统计损伤演化方程构建

3.2.1 冻土与结构接触面剪切微元强度定义

按照统计损伤理论，要求定义的接触面剪切微元随机损伤分布变量必须能够反映剪切微元是否破坏，故可以将剪切微元强度作为接触面剪切微元随机破坏分布变量。

依据冻土与结构接触面剪切破坏机理，参照摩尔-库伦强度破坏准则，同时综合考虑接触面温度、粗糙度和接触面法向应力对接触面剪切强度的影响，以冻结粉细砂与钢板接触面直剪试验得到的线性剪切强度极值多元回归分析为基础，对冻土与结构接触面剪切微元强度进行定义，如式(11)所示。

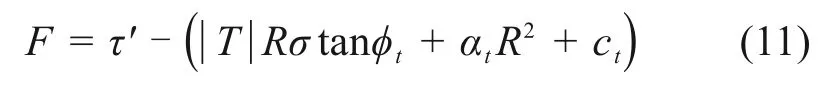
式中：F为接触面剪切微元强度；T为接触面温度；R为接触面粗糙度；σ为接触面法向应力；φt为接触面剪切微元屈服时内摩擦角；ct为接触面剪切微元屈服时黏聚力；αt为接触面剪切微元屈服时粗糙度拟合系数；ct，φt，αt可由不同接触面温度、法向应力及粗糙度条件下接触面直剪试验结果非线性回归拟合得到。

将式(9)代入式(11)，可进一步得到冻土与结构接触面剪切微元强度完整表达式，如式(12)所示。

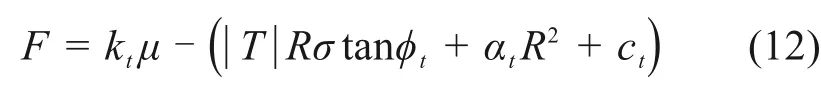
3.2.2 冻土与结构接触面剪切微元损伤破坏随机分布形式确定

依据统计损伤理论，假定冻土与结构接触面剪切微元强度F也服从双参数Weibull分布，冻土与结构接触面剪切微元损伤破坏的随机分布形式可以使用概率密度函数[14]表示，如式(13)所示。

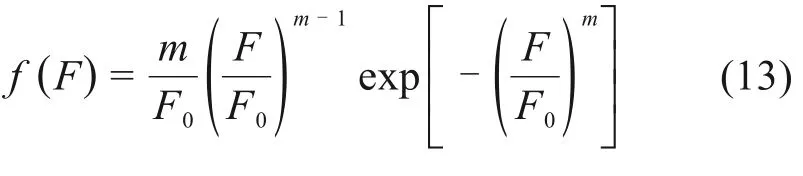
式中：F0，m为冻土与结构接触面剪切微元随机损伤破坏的概率密度函数的Weibull分布参数。

3.2.3 冻土与结构接触面统计损伤演化方程构建

根据冻土与结构接触面剪切破坏损伤因子定义，损伤因子即冻土接触面剪切微元随机损伤破坏统计概率，故利用积分原理推导出冻土与结构接触面统计损伤演化方程分段表达式[14]，如式(14)。

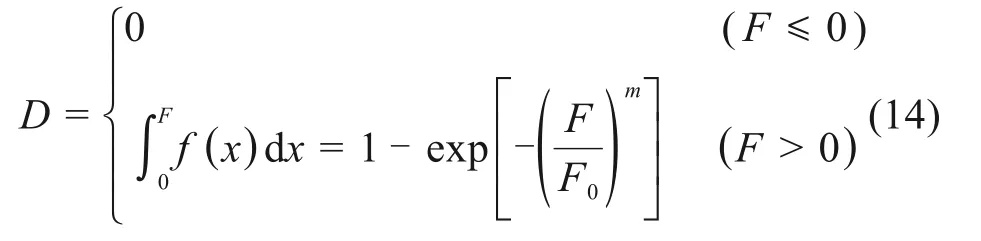
3.3 冻土与结构接触面剪切统计损伤模型构建

由上述冻土与结构接触面统计损伤演化方程和接触面剪切损伤模型，式(14)代入式(10)可推导冻土与结构接触面剪切统计损伤模型，如式(15)。

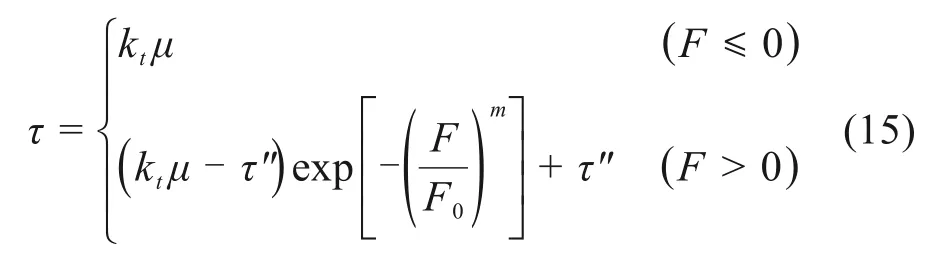
4 剪切统计损伤模型参数确定

构建冻土与结构接触面剪切统计损伤模型，最关键环节是如何合理确定冻土接触面剪切微元随机损伤破坏的概率密度函数的分布参数F0和m。为此，首先从特定剪切正应力条件下模型参数求解入手，继而进一步探讨普适性模型参数求解方法。

4.1 特定剪切正应力条件下模型参数求解

通过冻土与结构接触面直剪试验研究发现，接触面剪切变形过程中，剪应力存在着明显的极值和应变软化特征。因此，依据冻土与结构接触面剪切变形过程中的极值点，利用导数为0求极值方法，可求解特定条件下的统计损伤模型参数，如式(16)。

式中：μf为冻土与结构接触面剪应力峰值所对应的相对剪切位移。

式(16)中，当μ=μf时，也即在剪应力−剪切位移关系曲线中，其对应的剪应力达到冻土与结构接触面剪应力峰值τf，故将μ=μf代入式(15)，该统计损伤模型公式应当同样成立。同时将式(16)与式(15)联立求解，从而可以求解统计损伤模型参数m和F0，如式(17)～(18)所示。

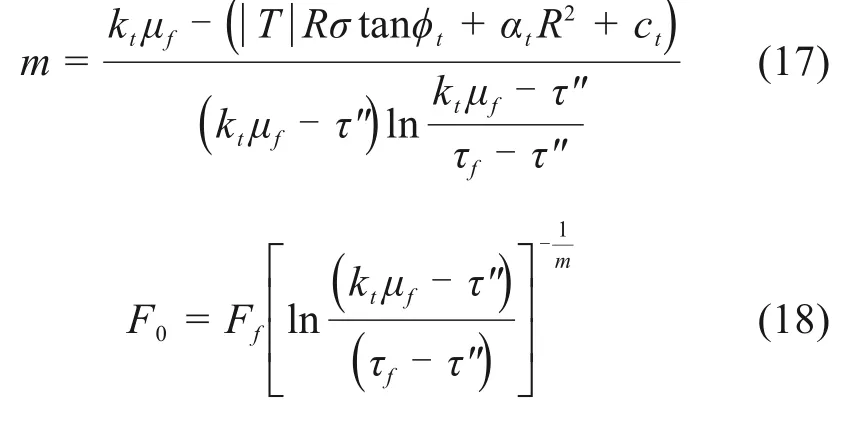
式中：τf为冻土与结构接触面剪应力峰值；Ff为中间过渡参数，其具体数值可由式(19)求得。

4.2 统计损伤模型参数通解

4.2.1τf求解方法

在冻土与结构接触面发生剪切变形过程中，当冻土与结构接触面剪应力达到峰值剪应力τf时，即认为接触面处冻土材料发生破坏。

依据冻土与结构接触面直剪试验结果，并结合冻土与结构接触面损伤本构关系定义可知：如图5，当相对剪切位移μ≤μf时，统计损伤模型中的接触面剪应力峰值τf即对应于直剪试验中的极限冻结强度τmax[17]，如式(20)；当相对剪切位移μ>μf时，冻土与结构接触面剪应力进入残余强度阶段，统计损伤模型中的接触面剪应力峰值τf则对应于直剪试验中的次峰值冻结强度τr-max[19]，如式(21)。

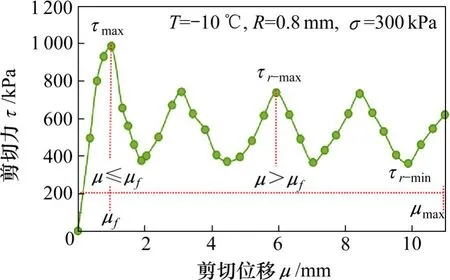
图5 τmax,τr-max,τr-min示意图Fig.5 Schematic diagram ofτmax,τr-max,τr-min

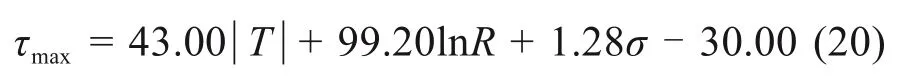
式中：τmax为冻土与结构接触面极限冻结强度；T为冻土与结构接触面温度；R为冻土与结构接触面粗糙度；σ为冻土与结构接触面法向应力。

式中：τr-max为冻土与结构接触面次峰值冻结强度。

综合式(20)和式(21)可以得到耦合接触面温度T，粗糙度R及法向应力σ的接触面剪应力峰值τf的分段函数关系式，如式(22)所示。

4.2.2τ″求解方法

通过对冻土与结构接触面直剪试验结果数据拟合，可以得到峰后冻结强度谷值τr-min，也即冻土与结构接触面残余剪切强度τ′r表达式，如式(23)。

式中：τr-min为接触面峰后冻结强度谷值。

4.2.3μf求解方法

通过不同工况条件下冻土与结构接触面直剪试验研究发现，在冻土与结构接触面剪切过程中，当冻土与结构接触面剪应力达到峰值剪应力τf时，其对应的相对剪切位移μf与冻土与结构接触面法向应力σ同样呈线性关系。因此，可由不同法向应力条件下冻土与结构接触面直剪试验结果经数据拟合得到μf的一次函数表达式，如式(24)所示。

式中：η，μ0分别为由不同法向应力条件下冻土与结构接触面直剪试验结果经数据拟合得到的一次项和常数项系数。

4.2.4 统计损伤模型参数通解

为进一步得到普适性的统计损伤模型参数，将式(19)，式(22)，式(23)，式(24)代入式(17)，式(18)，便可得到不同接触面温度T，不同接触面粗糙度R及不同接触面法向应力σ条件下冻土与结构接触面剪切统计损伤模型参数m和F0的通解表达式，分别如式(25)和式(26)所示。

5 接触面剪切统计损伤模型曲线特征

5.1 具体工况条件下剪切统计损伤模型参数确定

选定某一工况条件下(接触面温度T=−6℃，法向应力σ=500 kPa，粗糙度R=0 mm)冻土与结构接触面直剪试验结果，并以此为依据阐述冻土与结构接触面剪切统计损伤模型各个参数(式(15)，式(25)，式(26))的具体含义及其确定方法，各参数计算结果如表2所示。将T=−6℃，σ=500 kPa，R=0 mm代入式(22)即可得到冻土与结构接触面峰值剪应力τf的分段表达式，如式(27)所示。

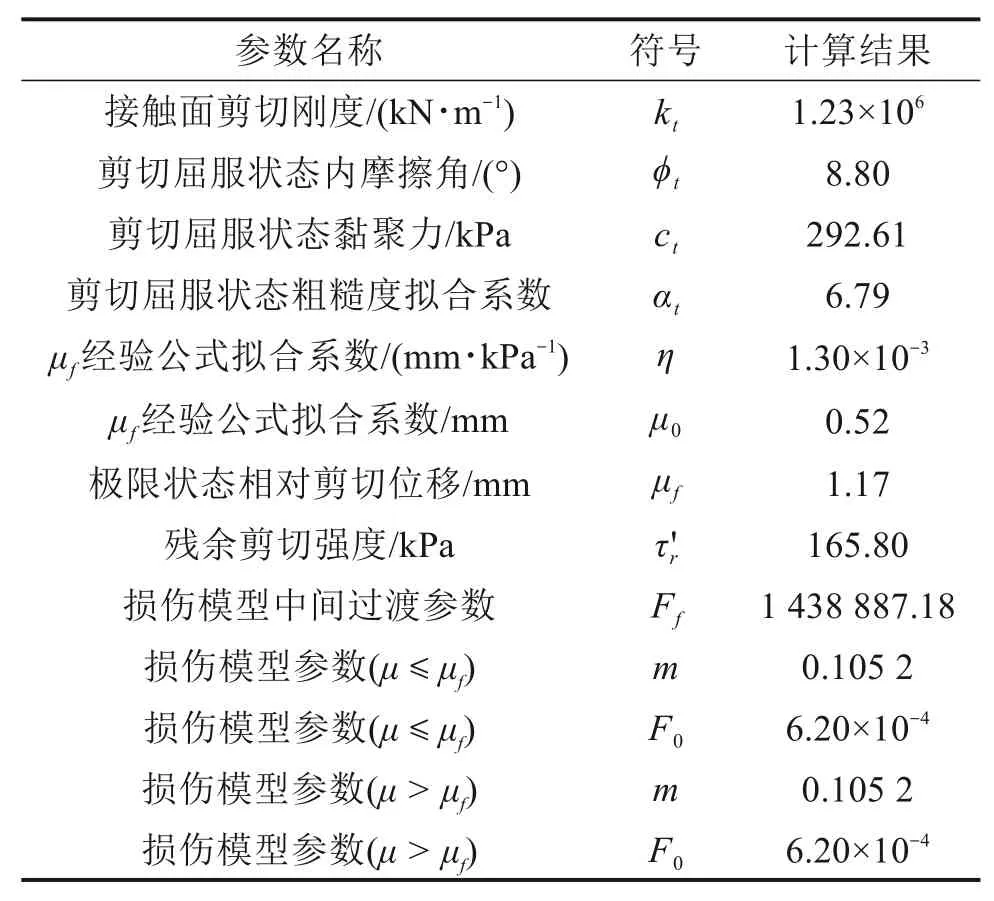
表2 统计损伤模型参数计算结果Table 2 Calculation results of statistical damage model parameters

将kt，φt，ct，αt，σ代 入 式(12)，并 令F=ktμ-(|T|Rσtanφt+αtR2+ct)=0，可 求 得F=0时分界相对剪切位移为0.173 mm，也即当μ≤0.173mm时，F≤0；当μ>0.173mm时，F>0。

因不同阶段接触面剪应力形成机理不同，故随相对剪切位移变化其接触面剪应力在分界位移点处产生突变，并由此造成相对剪切位移在分界处接触面剪应力值和切线位移非连续。将模型参数m及F0代入式(15)即可得到冻土与结构接触面剪切统计损伤模型的3段表达式，如式(28)所示。

5.2 具体工况条件剪切统计损伤模型曲线特征

为更直观了解该接触面剪切统计损伤模型模拟曲线特征，以接触面温度T=−6℃，法向应力σ=500 kPa，粗糙度R=0 mm工况条件为例，将接触面剪切统计损伤模型(式(28))模拟曲线和相同工况条件接触面直剪试验剪应力-相对剪切位移关系曲线解析到同一平面直角坐标系中，由此得到接触面剪切统计损伤模型模拟曲线与接触面直剪试验剪应力-剪切位移关系曲线对比情况，如图6所示。

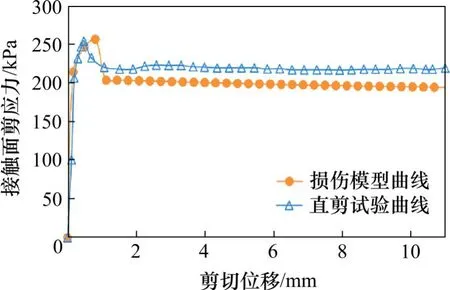
图6 模型模拟曲线与直剪试验剪应力−剪切位移关系曲线对比Fig.6 Comparison between model simulation curves and direct hear test curves under different interface temperature conditions

对比图6中模型曲线和试验曲线可发现：1)该统计损伤模型能较好模拟冻土与结构接触面剪切起始阶段线弹性变化特征，即接触面剪应力随相对剪切位移增加而线性单调递增；2)该统计损伤模型曲线在其应变硬化阶段随相对剪切位移增加而非线性单调递增，和冻土与结构接触面直剪试验曲线总体变化趋势相近；3)能较好模拟接触面剪应力达到峰值后随相对剪切位移增加而逐渐变小的应变软化特征；4)能较好模拟应变软化后剪应力随相对剪切位移持续增加而逐渐衰变的残余强度特性。

5.3 不同工况条件剪切统计损伤模型曲线对比

参照上述相同方法，进行不同接触面温度、不同法向应力条件补充直剪试验，并将补充直剪试验曲线与统计损伤模型曲线进行对比。

如图7为接触面法向应力σ=500 kPa，不同接触面温度条件(T=−2℃，T=−6℃，T=−10℃，T=−14℃)，如图8为接触面温度T=−6℃，不同法向应力条件(σ=100 kPa，σ=300 kPa，σ=500 kPa，σ=700 kPa)，补充直剪试验曲线与统计损伤模型曲线的对比情况。

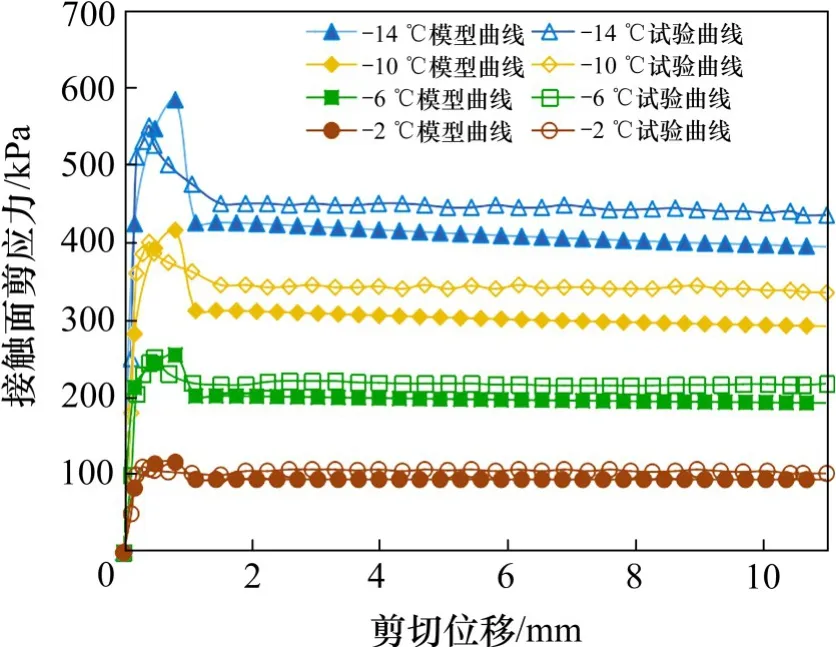
图7 不同接触面温度条件下模型模拟曲线与直剪试验曲线对比Fig.7 Comparison between model simulation curves and direct hear test curves under different interface temperature conditions

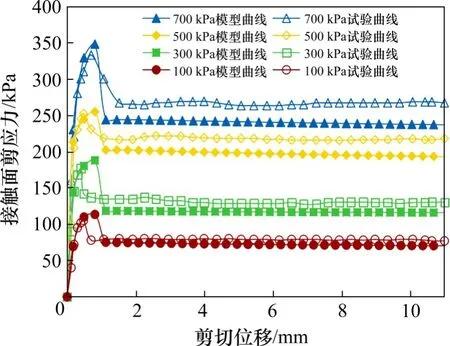
图8 不同法向应力条件下模型模拟曲线与直剪试验曲线对比Fig.8 Comparison between model simulation curves and direct hear test curves under different normal stress conditions

由图7～8可知，该统计损伤模型能够反映接触面剪应力随冻土与结构接触面冻结温度降低和接触面法向应力增大而增大的特性，且在不同接触面温度和不同接触面法向应力条件下，模型曲线与直剪试验曲线均具有一致的变化趋势。

6 结论

1)将统计损伤模型与不同工况条件直剪试验对比验证，结果表明：该接触面剪切统计损伤模型能较好模拟冻土与结构接触面剪切变形中线弹性、应变硬化、应变软化及残余强度等典型变化特征。

2)该接触面剪切统计损伤模型能模拟多种实际工况条件，并通过kt，φt，ct，αt，T，R和σ等统计损伤模型参数直观反映接冻土触面冻结温度、粗糙度、法向应力等对接触面剪切强度的影响。

3)该接触面剪切统计损伤模型能够模拟包括残余剪切强度τ′r在内的接触面剪切强度总体变化趋势，但尚不能精确模拟接触面残余冻结强度周期性波动。

4)该接触面剪切统计损伤模型形式简单，均采用常规力学参数kt，μ和σ等，便于统计损伤模型理解、推广及应用，可为冻土与结构接触面冻结强度预估和数值模拟研究等提供基础理论模型。