地震作用下含岩桥边坡系统可靠性分析
2021-11-13李亮文子祥王中伟唐高朋赵炼恒
李亮,文子祥,王中伟,唐高朋,赵炼恒,3,4
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中铁上海局集团 第五工程有限公司,广西 南宁 530000;3.中南大学 高速铁路建造技术国家工程实验室,湖南 长沙 410075;4.中南大学 轨道交通工程结构防灾减灾湖南省重点实验室,湖南 长沙 410075)
岩质边坡的破裂面受其地质结构影响很大[1]。软弱结构面(如层理面、裂纹和节理面)广泛分布在岩体中,并且在稳定性分析中起着至关重要的作用,它们为岩质边坡滑塌提供了潜在的滑动路径。潜在滑动路径的不同将导致破坏模式的不确定性[2]。因此,有必要引入系统可靠性方法来分析多种潜在破坏模式下岩质边坡的稳定性。岩质边坡的破坏模式与节理面分布有关,沿节理面滑动作为岩质边坡一个代表性的破坏机制,在现有研究中被广泛用于分析岩质边坡的系统可靠性[3−5]。在以往的研究中,节理面通常被视为连续的平面。然而自然界中,节理面的连通性存在被岩桥截断的情况[6−8]。滑动面的总剪切强度由于岩桥的存在而显著增强,因而岩桥对边坡稳定性起着重要作用[9−10],尤其是在以平面滑动为主的沉积岩中。岩桥的破裂通常归因于剪切、挤压、张拉或这些因素的组合。考虑到其复杂的力学行为,现有研究通常是基于某些假定,然后应用有限元、离散元、模型试验或理论分析等方法来分析岩质边坡的稳定性[11−14]。在这些方法中,JENNINGS[13]首先提出了用于来评估含岩桥的边坡稳定性的方法(以下简称JENNINGS法)。该方法假定含非连续节理的剪切滑动岩体在向下滑动时会出现较为平坦的破裂面且会穿过岩桥,边坡的安全系数可通过极限平衡法计算得到。尽管JENNINGS法在复杂条件下并不适用[3,6],但它可以提供一个合理的简化公式,用于评估在岩桥之间含共面节理岩质边坡(平面滑动模式)的稳定性,尤其是在有较高节理连通率的情况下结果更为可靠[11]。在岩质边坡失稳的众多外部诱发因素中,已有研究主要关注地下水的影响[3−4,15−16]。然而,地震作为强破坏性的自然灾害,对岩质边坡的失稳也有重要影响。目前,考虑地震的影响对边坡进行系统可靠性研究也有一定的发展,但是在含岩桥的边坡在地震作用下的系统可靠性分析尚有待完善。一般情况下,有4种方法常用来评估地震作用下边坡的动力响应:Newmark位移法、拟静力分析法、动态有限元分析方法和模型试验方法[17−18]。拟静力分析法由TERZAGHI[19]首次提出,是地震作用下边坡稳定性分析最常用的方法。该方法将地震作用简化为作用在滑体质心的等效静力荷载。由于其简便易用的特性,已被大量研究人员[20−21]采用。基于以上考虑,本文主要对岩桥型滑坡边坡在地震作用下的系统可靠性进行分析。采用拟静力法考虑地震的水平地震效应和竖向地震效应,基于极限平衡法给出了各破坏模式下边坡安全系数的计算公式。然后,根据各破坏模式的独立性和相关性,构造了一个可靠性系统,并基于MATLAB编写了计算程序。最后,采用拉丁超立方体方法,利用计算程序对边坡几何参数、地震效应等参数进行了分析。
1 考虑地震作用的含岩桥边坡平面滑动模型
1.1 平面滑动模型
含竖向裂缝岩质边坡的平面滑动面模型是由HOEK等[12]首次提出的。在这个基础上,许多研究者考虑孔隙水压力[2]、倾斜张拉裂缝[7]、多重相关破坏模式[5,15]或这些因素的组合等开展进一步的研究。本文主要分析含岩桥的边坡在地震作用稳定性,改进了已有的平面滑动模型,将整个系统分为包含2个含岩桥的相连滑块(滑块A和滑块B)。岩质边坡模型的几何示意图如图1所示。
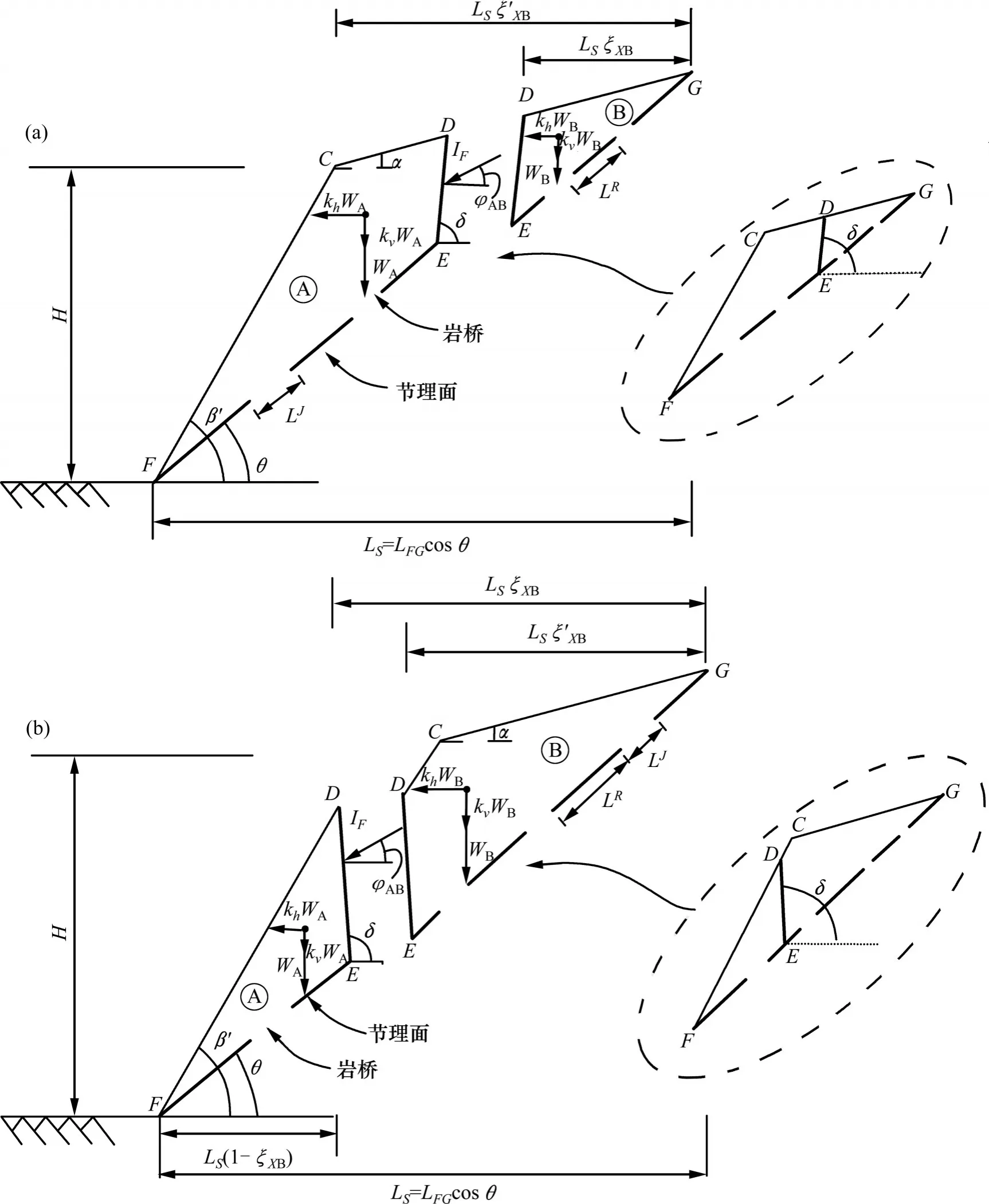
图1 破坏模式示意图Fig.1 Failure mode diagram
其中:H是边坡高度;β'是坡角;θ是滑动面角度;α是顶面的倾斜角度;φAB是相互作用力IF的倾角;LJ,LR分别为节理面及岩桥的长度;δ是张拉裂缝的倾角。张拉裂缝的位置取决于ξ′XB-ξXB的值:当ξ′XB-ξXB<0时,裂缝位于坡体顶部;当ξ′XB-ξXB<0时,裂缝位于坡面。ξ′XB可 由 式(1)得到:

上式用到的几何参数见附录1。
1.2 岩桥和地震作用
对于由岩桥隔断的共面节理,通常用节理连通率K定义滑动面上非连续节理的占比,K可根据Jennings提出的公式计算得到[13]:
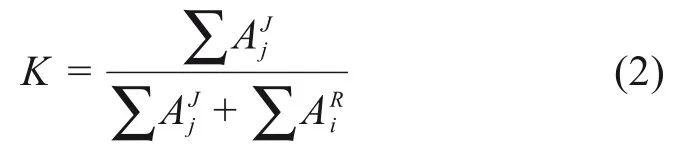


其中:cR,φR和cJ,φJ分别是岩桥和节理面的黏聚力和内摩擦角。
地震作为诱发边坡失稳的主要因素,对边坡稳定性有着重要影响。拟静力分析方法将地震效应等效为一系列水平方向和竖直方向上的恒力(分别是Fh=khW和Fv=kvW)。因此,地震效应在水平方向上的拟静力系数kh(kh=ah/g)和竖直方向上的拟静力系数kv(kv=av/g)可分别用于表征水平和竖直方向上的地震作用。其中av和ah分别为地震作用下数值和水平方向上的加速度,g为重力加速度。若kv为正,则意味着垂直方向的地震作用竖直向下,若kv为负,则意味着垂直方向的地震作用竖直向上。kh的方向由边界条件决定。通常kh被认为水平作用于自由面(方向朝向坡体外侧),如图1所示。
1.3 稳定性分析
对于含岩桥的平面滑动模型,本文基于极限平衡法考虑下滑力和抗滑力之间的静态平衡条件,得出安全系数的计算公式如下[22]:其中:Fresisting是沿破裂面的总抗滑力;Fdriving是沿破裂面的总下滑力。

根据岩块之间相互作用的不同,潜在破坏模式主要可归为2类:
情况1:块体A和B间无相互作用
滑块B保持稳定,不对滑块A产生任何作用力。即滑块间无相互作用,此时仅需要考虑滑块A的稳定性。滑块A的抗滑力和下滑力可由式(6)和式(7)可得:
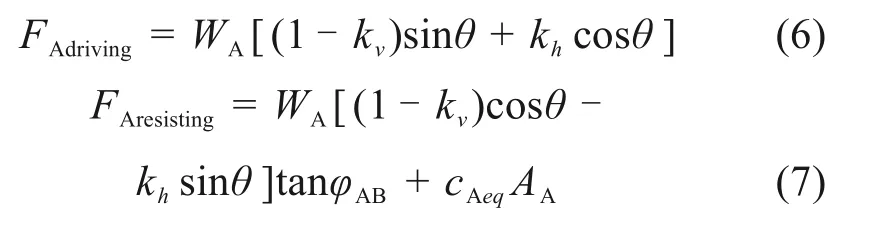
将式(6)和式(7)代入式(5)中,即可得到安全系数表达式如下:

同理,滑块B的安全系数如下:
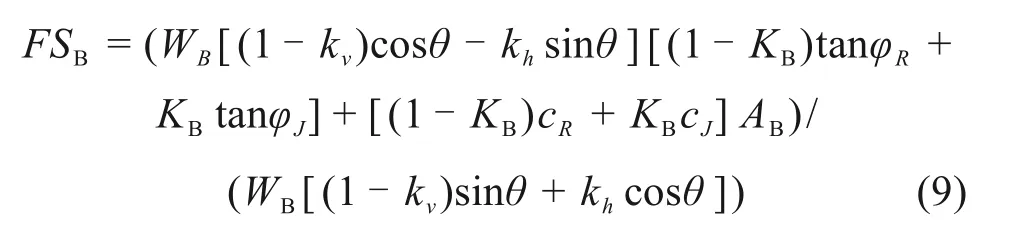
其中:KA和KB分别为滑块A和B的节理连通率;AA和AB分别为滑块A和B的滑动面面积;WA和WB分别为滑块A和滑块B的重量。AA,AB,WA,WB的表达式详见附录。
情况2:块体A和B间有相互作用
滑块B失稳滑动,因相互作用力带动滑块A的失稳。因此,2滑块间的相互作用力IF可通过将滑块B的安全系数设为1计算得到[2,5]。然后基于极限平衡方法,可得安全系数,如式(10)所示。

2 系统可靠性方法
2.1 4种潜在破坏模式
对于岩质边坡而言,可以根据张拉裂缝的位置和滑块B的稳定状态定义4类潜在破坏模式。破坏模式1:张拉裂缝位于坡体顶部,滑体B稳定而滑体A不稳定(无相互作用);破坏模式2:张拉裂缝位于坡体顶部,滑块A和滑块B均不稳定(有相互作用);破坏模式3:张拉裂缝位于坡体表面,滑块B稳定而滑块A不稳定(无相互作用);破坏模式4:张拉裂缝位于坡体表面,滑块A和滑块B均不稳定(有相互作用)。
2.2 系统可靠性模型
当上述任意一种破坏模式发生时,即边坡系统发生了破坏。当边坡发生破坏时,也仅会出现上述破坏模式中的一种破坏模式。因此,边坡系统包含了4种破坏模式的子系统。且子系统之间互不影响。由于不同模式之间的相关性可以忽略,因此系统破坏概率Psf可以表示为各种模式破坏概率之和:

其中:NCS表示子系统的数量;Ek表示第k个子系统的破坏状态。值得说明的是,如果破坏模式之间存在相关性而没考虑在内,将会高估破坏概率,导致计算结果偏于保守[4]。对于岩质边坡而言,2个约束条件(裂缝的位置和滑块B的稳定状态)需要用于定义不同的子系统。此外,当安全系数小于1时子系统的将发生破坏。当这3个条件同时满足时,子系统将发生破坏。极限状态函数和系统组合如表1和图2所示。
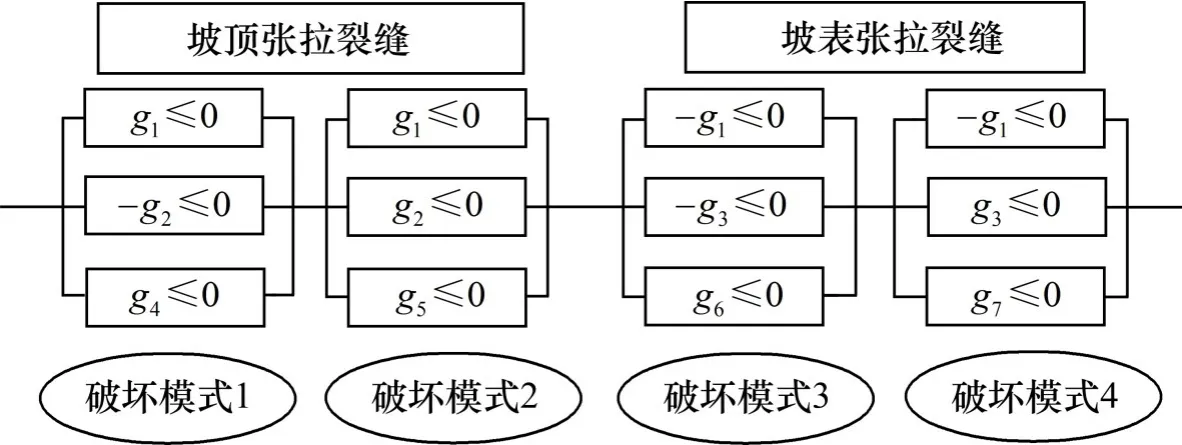
图2 系统构成Fig.2 System composition

表1 组合极限状态函数说明Table 1 Interpretation of component limit state functions
为了计算系统可靠性,应首先计算每个子系统的可靠性。蒙特卡洛方法(MCS)可以提供一个高度精确的结果。但是该方法非常耗时,尤其是对于某些罕见事件。拉丁超立方体抽样(LHS)作为一个无替代抽样的分层抽样方法,可有效应用到本研究中以提高抽样效率。相较于常规的MSC方法,该法已经被证明在少量样本的情况下仍能有较大概率达到收敛状态[23]。
对于由LHS方法产生的N个样本,系统破坏概率Psf可由式(13)计算:

其中:NF表示破坏的总数;表示第i个子系统的破坏概率,可由计算得到;其中是第i个子系统的破坏数量。根据El-RAMLY等[8]和CHOWDHURY等[4]的研究结论,对应的可靠性系数β可由式(14)给出:

其中:σ[FSB]和E[FSB]分别是安全系数FSB的标准差和平均值。
3 系统可靠性方法的分析结果
本研究的岩质边坡随机及确定性参数如表2所示,各随机变量的相关关系如表3所示。

表3 随机变量相关矩阵Table 3 Correlation matrix of random variables
3.1 2类抽样方法的对比
在本节中,对比了LHS方法与MCS方法的模拟效果,来验证LHS方法的有效性。边坡模型如图1所示,计算参数选取为γ=24 kN/m3,H=46.5 m,α=11°,β=56.4°,θ=25°。其他确定性参数为:ξXB=0.73,φAB=25°,δ=120°,KA=0.9,KB=0.9。考虑到地震荷载的影响,相关参数取值为:kv=0.1,kh=0.3。假定岩桥和节理面的剪切强度参数为随机变量并服从对数正态分布(见表2)。同时,通过引入这些随机变量的相关矩阵(表3)考虑其相关关系。LHS与MCS方法下的系统破坏概率随模拟样本变化趋势如图3所示。
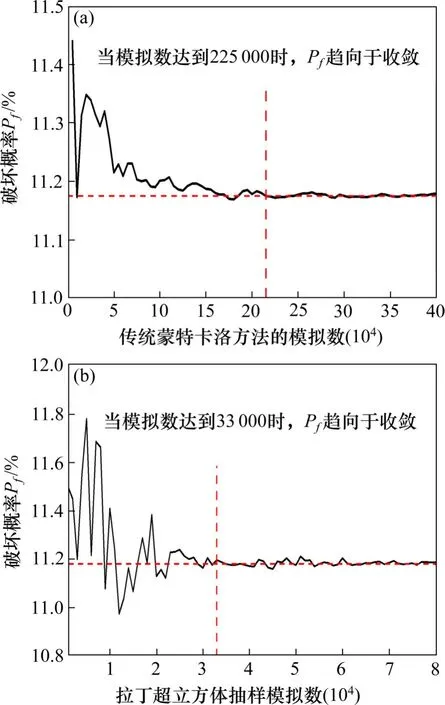
图3 系统破坏概率随模拟样本的变化Fig.3 Change of system failure probability with simulated samples
如图4所示,在LHS方法下,当接近33 000个模拟样本时,岩质边坡系统破坏概率将收敛于11.7%。而在常规MCS方法下,需要225 000个模拟样本才能使得结果收敛。该结果证实了相较于MCS方法,LHS方法更为高效。为了在较短的计算时间内获取相对准确的结果,本文中所有案例中均采用LHS方法生成50 000个模拟样本进行分析。
3.2 每种破坏模式的影响
为了分析各种破坏模式的影响,假定KA=0.85,KB=0.85,kv=0.1,kh=0.3和δ=120°,其他参数按照表2选取。同时考虑所有随机变量的相关关系(见表3)。系统破坏概率(psf)和各种破坏模式下的破坏概率随边坡高度的变化如图4所示。
如图4所示,系统破坏概率和各模型下破坏概率会随着边坡高度的增大而增大。坡高对不同破坏模式的相对影响存在差异性。破坏模式1在边坡高度下对系统破坏概率的影响始终最大。其次是破坏模式3。破坏模式2的贡献相对较小,但它的影响会随着边坡高度的增大而增大。且随着边坡越高,增长趋势越明显。破坏模式4的贡献最小,其破坏概率几近于常数。分析结果表明,滑块A在稳定性评估中具有重要作用。此外,破坏模式1和3中比破坏模式2和4对psf的贡献大。这表明,在滑块A和滑块B之间无相互作用相对于有相互作用的破坏概率更大,说明仅考虑滑块A的失稳可能会低估边坡的破坏概率。
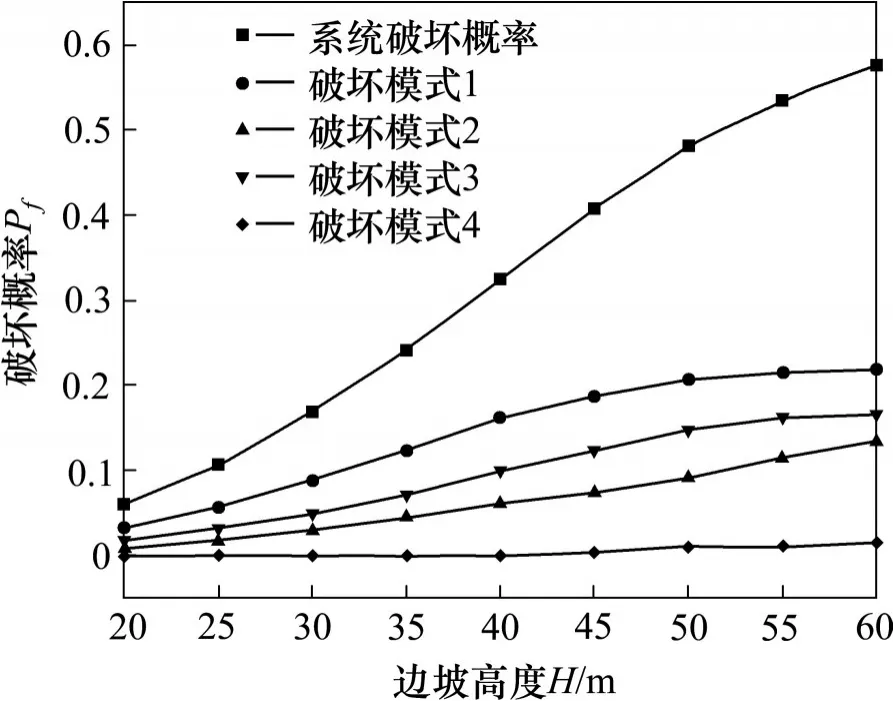
图4 系统及各种破坏模式的破坏概率随边坡高度的变化Fig.4 Computed probability of failure for the overall system and each failure model versus slope height
3.3 地震效应对含节理岩质边坡稳定性的影响
为了分析地震作用的影响,假定H=60 m,KA=0.8,KB=0.8,KA=0.9,KB=0.9。考虑2种地震作用情况:1)仅考虑水平地震作用,此时kv=0.0,kh在0~0.4范围内变化;2)综合考虑水平地震作用和垂直地震作用,此时kv在−0.2~0.2之间变化,kh=0.4。其他参数与3.2节一致。2种地震作用情况下的系统破坏概率如图5所示。
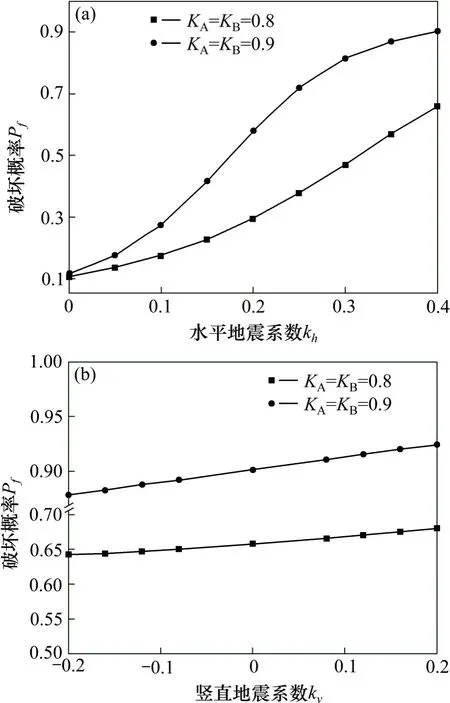
图5 2种地震作用下的系统破坏概率Fig.5 System probability of failure under two differentseismic actions
如图5(a)所示,仅考虑水平地震作用时,psf随着kh的增大而急剧增大。当KA=0.8,KB=0.8时,破坏概率从11.0%(无地震作用)增长到65.5%;当KA=0.9,KB=0.9时,破坏概率从12.6%(无地震作用)增长到88.6%。这表明psf对水平地震作用非常敏感。如图5(b)所示,当kh保持不变时(kh=0.4),KA=0.8,KB=0.8和KA=0.9,KB=0.9。2种情况下,psf随kv的变化非常相近。psf随着kv的增大而增大,但增长速率较为平缓。例如,当KA=0.8,KB=0.8时,破坏概率从64.2%(kv=−0.2)增长到67.9%(kv=0.2);当KA=0.9,KB=0.9时,破坏概率从87.8%(kv=−0.2)增长到92.4%(kv=0.2),这表明,竖直地震作用对平面岩质边坡的影响相对有限。
3.4 岩桥的影响
为了分析岩桥对系统可靠性的影响,假定H=60 m,KA和KB均从0.5变化到1.0,其他参数及随机变量之间的相关关系与3.2节保持一致。系统破坏概率如图6所示。
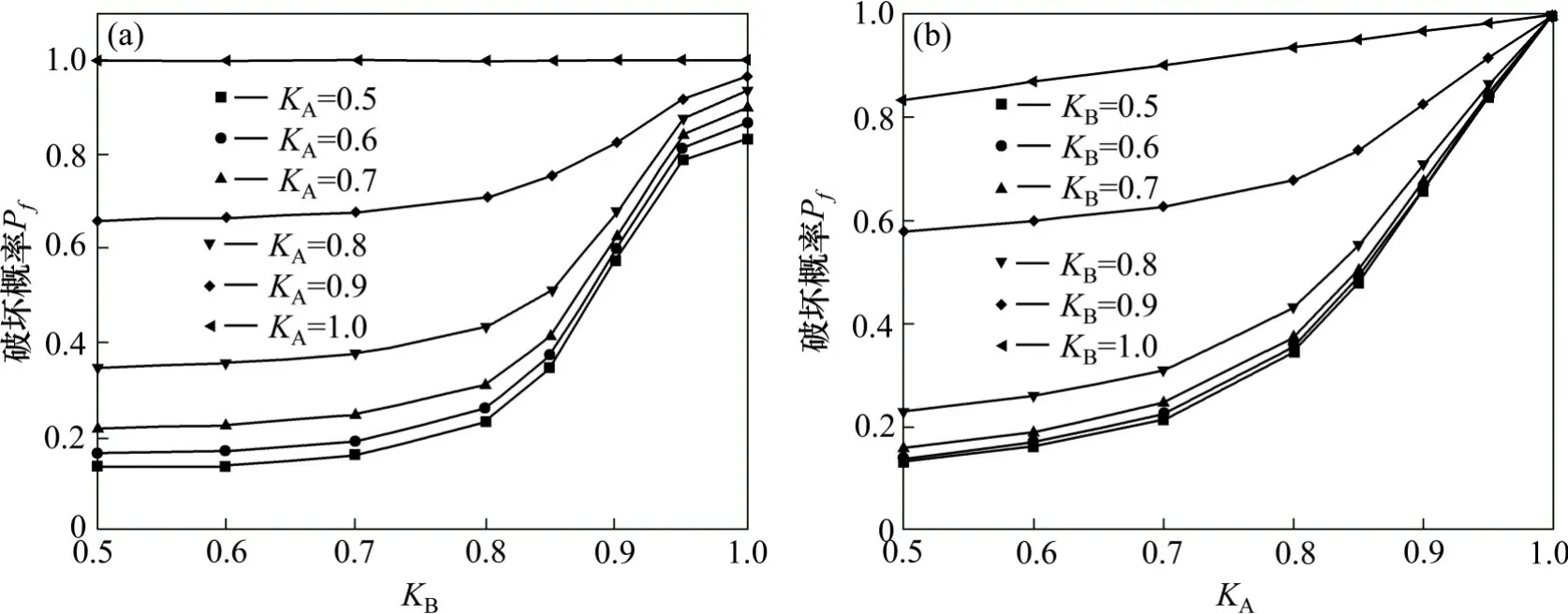
图6 不同节理连通率下的岩质边坡系统破坏概率Fig.6 System probability of failure for different joint connectivity rates of rock slope
如图6(a)所示,对于大多数曲线(KA=0.5~0.80),psf会随着KB的增大而缓慢增大,直到KB=0.8。在这之后,psf将会急剧增长。对于曲线KA=0.9,系统破坏概率的增长则会随着KB的增大而较为平缓地增长。尤其当KA=1.0时,滑块A的节理段完全连接,系统破坏概率达100%,将不会受到滑块B节理连通率的影响。如图6(b)所示,对于大多数曲线(KB=0.5~0.8),psf会随着KA的增大而显著增大,但是对于KB=0.9和KB=1.0,增长趋势会趋于平缓。当KB=1.0时,滑块A的节理段完全相连,系统破坏概率并不是100%,但会随着KA的增大而缓慢增大。因此,psf对滑块A的节理连通率较滑块B更敏感。这表明滑块A对系统稳定性的评估更加重要。
3.5 张拉裂缝倾角的影响
为了分析张拉裂缝倾角的影响,假定H=60 m,且ξXB设定为常数。利用2个不同的ξXB值来表征张拉裂缝的不同位置:ξXB=0.6和ξXB=0.85分别表示张拉裂缝位于坡体顶部和表面。在ξXB=0.6的情况下,δ从45°到110°之间变化;而在ξXB=0.85的情况下,δ从60°变化到120°。其他的参数和随机变量间的相关关系与3.2节一致。2种张拉裂缝位置下psf和可靠性系数β随张拉裂缝倾角的变化曲线如图7所示。
如图7所示,2种张拉裂缝位置下,随着δ的增大,psf均随之减小,随着β的增大,psf均随之增大。如图7(a)所示,当张拉裂缝位于坡体顶部时,psf随着δ的增大而急剧减小,从65%降至35%。这表面当裂缝位于坡体顶部时,psf对裂缝倾角较为敏感。如图7(b)所示,当裂缝位于坡体表面时,psf随着δ的增大而减小,但是在倾角范围60°~120°间变化较小。例如,破坏概率从δ=60°时的9.6%减少到δ=120°时的9.2%,仅减少了0.4%。这表明psf对位于坡体表面的张拉裂缝形状并不敏感。上述结论同样表明张拉裂缝倾角对系统可靠性的影响极大程度上取决于其位置,张拉裂缝位于坡体顶部较位于坡体表面时,倾角的变化对边坡破坏概率影响更大。
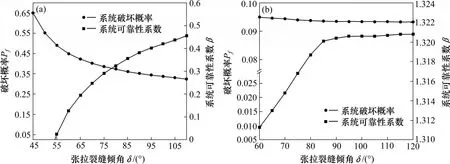
图7 张拉裂缝倾角的影响Fig.7 Effect of the tension crack inclination
4 结论
1)通过对比MCS法可以发现,LHS法更为高效,利用更少的模拟样本即可获得准确结果。
2)不同破坏模式的相对影响不相同,破坏模式1对psf的影响最大。这表明了滑块A在稳定性评估更加重要,因此其稳定性在设计中应该优先考虑。破坏模式1和3对psf的影响比破坏模式2和4更为显著。这表明滑块间没有相互作用的破坏模式相对于有相互作用的破坏模式更加容易出现。
3)边坡的破坏概率随水平地震系数kh和竖直地震系数kv的增大而增大。水平地震系数kh对系统可靠性影响显著,而竖直地震系数kv的影响较为有限。水平地震作用在评估岩质边坡可靠性时应该优先考虑。
4)岩桥对边坡稳定性具有重要影响。主要体现在节理连通率对系统可靠性具有重要影响,边坡的破坏概率随节理连通率的增大而增大,对具有较高节理连通率的岩质边坡而言更为显著。
5)张拉裂缝倾角δ对系统可靠性的影响在很大程度上取决于其位置。当张拉裂缝位于坡体顶部时,δ对系统可靠性具有显著影响;而当裂缝位于坡面时,δ对系统可靠性的影响较小。
附录1:边坡几何变量计算
对于位于坡体顶部的张拉裂缝(图1(a)),其长度LDE可由式(A1)表示:

其中

其中LDG,LFG,LCF分别为边坡几何线段DG,FG,CF的长度。LS是LFG的水平向长度。
LEF和LEG的长度可由式(A6)和(A7)得到:

破裂面的面积AA和AB可由式(A8)和(A9)得到:

楔体的面积ADEG和ACDEF可由式(A10)得到:

如图1(a)所示,滑动楔体的重量WA和WB可由式(A12)和(A13)计算:

其中:γR是岩体单位重量,kN/m3。
对于位于坡面的张拉裂缝,其长度LDE可由式(A14)得到:

其中

其中:LDF是边坡几何线段DF的长度;LS可由公式A4得到。
滑块A和滑块B的破裂平面长度LEF和LEG可由式(A16)和(A17)得到:

破裂面面积AA和AB可由式(A18)和(A19)得到:

楔体的面积ADEF和ACDEG可由式(A20)得到:

如图1(b)所示,滑动楔体的重量WA和WB可由式(A22)和(A23)得到:

