纤维铺放压辊变形建模与分析

赵盼, 吴博, 史耀耀, 史恺宁, 胡昊, 陈振, 俞涛, 孙鹏程

(1.西北工业大学机电学院， 陕西西安 710072;2.西安明德理工学院智能制造与控制技术学院， 陕西西安 710124;3.空装驻西安地区第二军事代表室， 陕西西安 710021;4.西安电子工程研究所， 陕西西安 710100;5.西安应用光学研究所， 陕西西安 710065)

树脂基复合材料因其具有可设计性、各向异性、材料和结构一体化以及复合效应等特点,使其具有性能可设计、高比强度、高比刚度、耐高温、耐疲劳、耐腐蚀、阻尼减震性好、破损安全性好、易于成型大型零件等优点[1,2]。作为21世纪最重要的材料之一,先进树脂基复合材料在航空、航天与汽车等工业领域扮演着越来越重要的角色[3]。先进树脂基复合材料的成型方法很多,常用的有手糊成型、拉挤成型、树脂传递模塑成型、树脂膜渗透成型、缠绕成型、铺放成型等[4]。纤维铺放(fiber placement)技术在纤维铺放系统与机器臂相结合的基础上,能够精确、高效加工大曲率复合材料制品[5]。

纤维铺放工艺过程中,不仅铺层顺序与铺层方向会对最终的制品性能产生影响,而且关键成型工艺参数铺放压力、热气炬温度和铺放速度对层合板的质量也产生重要影响,最终影响制品的性能[6]。李靖等针对铺放成型过程中热风枪温度、铺放速度、压辊压力、压辊温度和底板温度等工艺参数对复合材料板材层间剪切强度的影响进行研究,得出压辊压力对板材的层间剪切强度影响最大,在合适范围内,升高压辊压力有利于材料层间剪切强度的提升[7]。Aized等对纤维铺放工艺过程进行分析,利用响应面法建立了铺放压力、热气炬温度和铺放速度与铺放质量之间的回归模型,并对工艺参数进行耦合优化,最后得到了纤维铺放工艺参数的最优组合[8]。Levy等基于层间结合模型,建立了预浸带铺层制品的性能预测模型,并根据预测模型调节成型过程中温度和压力;同时采用显微镜测量法,验证了优化调节能够提高最终制品性能的稳定性[9]。其次,众多学者针对铺放工艺参数作用过程进行优化,提高制品性能。Yu等提出了复合材料预浸带缠绕工艺多参数相对灵敏度分析和单参数灵敏度分析的方法,计算关键工艺参数的相对灵敏度,确定了每个参数的稳定域和非稳定性域,并对复合材料缠绕工艺参数进行优化,最终获得了层间剪切强度工艺参数的优化范围[10]。段玉岗等针对纤维铺放过程中芯模表面的压紧力分布均匀性问题进行研究,对不同弹性模量的压辊材料进行了试验分析,结果表明,低弹性模量的压辊材料变形较大,较好地适应了芯模表面,压力分布相对均匀且可以减少铺层的层间孔隙数量,硅橡胶压辊比聚乙烯压辊压紧力分布均匀性提高了50%～60%,铺层孔隙率降低了92.1%[11]。

从现有研究来看,国内外学者针对纤维铺放构件层间粘结强度预测的研究主要集中在铺放工艺过程中工艺参数单因素及多因素耦合对层间粘结强度的作用机理方面的实验研究。但是铺放压辊与基体接触压应力分布机制方面研究较少,故本文将对纤维铺放过程中压辊变形过程与压辊压应力分布开展深入地分析与讨论。通过分析铺放过程中压辊作用过程,建立压辊压应力分布模型,进而获得接触压应力、压辊下压量以及压辊与基底的变形接触区域之间的映射关系,并通过实验验证了该模型的有效性。

1 压辊变形分析

在纤维铺放过程中,钢质压辊能够在铺放过程中精确控制厚度,但在进行曲面铺放时,钢质压辊与曲面为点接触,当压辊的半径大于曲率变化区域的半径时,钢质压辊与基底之间会产生间隙,如图1所示。该间隙导致无法均匀的施加压力将预浸纤维丝束铺放至曲面表面,影响层间结合度,进而影响制品的最终性能。

图1 复合材料纤维铺放成型过程

不同于钢质压辊,橡胶压辊在压力作用下会产生变形,即使在相同的铺放压力下,具有不同弹性模量的压辊也将产生不同程度变形。这种变形将增加压辊与基底接触的面积,大大改善层间结合度。同时在使用纤维铺放技术对复杂曲面结构进行铺放时,当压辊半径大于曲率变化区域半径时,橡胶压辊表面能够更有效地贴合芯模表面,更容易匹配零件表面几何形状,避免该区域因层间结合度不足而影响整个复合材料部件的机械性能。

在铺放过程中,铺放压力由铺放装置内的气缸提供,并最终通过压辊将压力施加到预浸纤维表面。在压力作用下橡胶压辊变形形成的铺放接触区域,如图2所示。

图2 橡胶压辊变形接触区域

压辊的橡胶部分由硅橡胶制成。由于该材料的非线性特性,所以橡胶压辊的变形是不规律的。随着铺放压力增高,橡胶压辊的变形量也随之增加,同时铺放区域的接触面积也相应增加。在纤维铺放过程中,橡胶压辊与基底表面接触变形的截面形状如图3所示。

图3 橡胶压辊与基底纤维丝实际接触面

由图3可知,在压辊与基底的实际接触过程中,会产生2个接触区域。区域1产生于橡胶压辊接触预浸丝束时,由橡胶压辊的变形产生。区域2产生于压辊向前移动时,由预浸纤维丝束厚度方向受压变形产生。当铺放压力增加时,接触区域1的长度和接触区域2的长度均增长。由于常用预浸纤维的厚度小于1 mm,导致铺放过程中接触区域1的长度远大于接触区域2的长度,且接触区域1内接触曲线的曲率较小。因此,在实际计算过程中将接触区域1简化为一条直线,忽略不计接触区域2的长度。铺放过程中橡胶压辊和预浸纤维丝束的简化变形,如图4所示。基于图4,橡胶压辊与基底表面之间的接触长度可由公式(1)与(2)计算得出。

图4 橡胶压辊简化变形

(1)

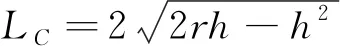
(2)

式中:α/(°)为铺放压力作用方向与力作用区域边界之间的夹角;r/m为压辊的直径;h/m为压辊在铺放压力作用下垂直方向上的高度变形量;LC/m为压辊与基底表面之间的接触长度。

在铺放过程中,橡胶压辊的底部承受摩擦力和法向压力,其中压辊旋转的动作是由摩擦力产生,且摩擦力为水平方向;铺放压力等同于法向压力,且为垂直方向。压辊底部的变形不均匀,因此压辊与基底芯模接触面上的法向分布也为非均匀分布。

2 压辊压应力分布建模

铺放平台所用压辊直径为25 mm,中心轴直径10 mm,沿橡胶层中心径向均布12个直径为2.5 mm的圆孔,用于增大压辊变形后与基底的接触面积。压辊为硅橡胶材质,其密度为1.1 g/cm3,杨氏模量为0.007 8 GPa,泊松比为0.47。基底芯模为铝材质,其密度为2.7 g/cm3,杨氏模量为69 GPa,泊松比为0.32。为获得其铺放过程压应力分布,本节采用有限元法进行分析,压辊与基底的网格类型为CPE4R,网格尺寸为0.2 mm,摩擦因数为0.15,预浸纤维全约束,压辊沿预浸纤维丝束铺放方向约束,垂直方向下压量为3 mm,压应力有限元分析结果如图5所示,压应力分布如图6所示。

图5 压辊受力变形有限元分析

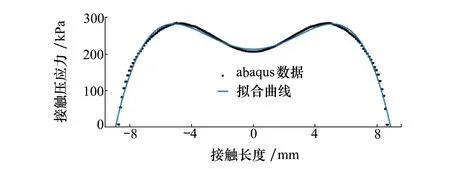
图6 压辊压应力分布

由图6可以看出,由于压辊沿径向方向均布了一圈小孔,该小孔导致在压辊压应力分布顶部区域出现一个小凹陷,该凹陷随着压辊在铺放过程中的转动沿分布的顶部区域相应左右移动,但不影响压辊压应力整体的分布规律。图中,对abaqus获得的数据进行最小二乘拟合,该四次曲线可以有效地拟合出铺放压应力与接触区长度的关系。

由于不同的压辊下压量产生的压辊与基底的接触曲线不同,采用相同的拟合方式,对不同压辊下压量时接触区域压应力分布曲线进行拟合,各拟合曲线如图7所示。不同压辊下压量时,压辊变形接触区域压应力分布曲线拟合系数如表1所示。

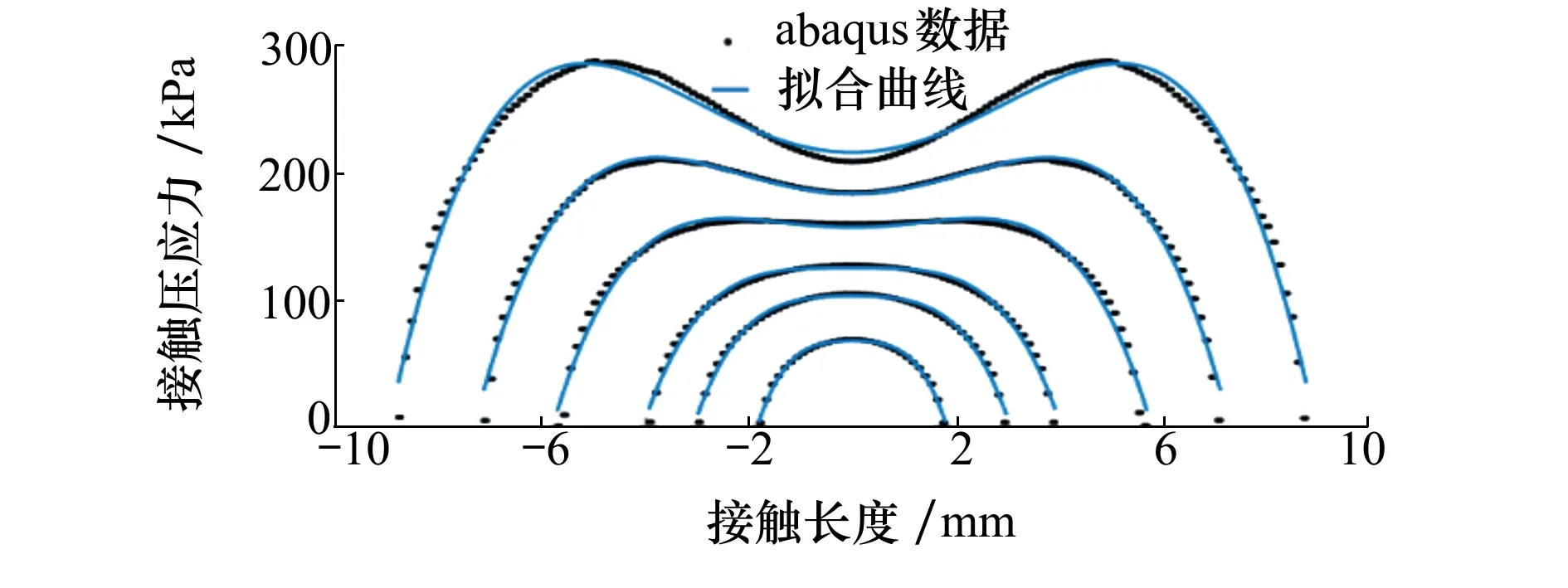
图7 不同压辊下压量时接触区压应力分布曲线与拟合曲线

表1 不同压辊下压量时压辊接触区域压应力分布曲线拟合系数

R2:决定系数

对图7所示曲线拟合,铺放压应力、压辊下压量与接触区域长度的函数关系如公式(3)所示。

(3)

式中:f(xc,h)为接触区点(x,h)处接触压应力;pc1至pc5为关于下压量h的函数,如公式(4)～(8)所示。

基于公式(3)至(8),可知abaqus分析结果、曲线拟合结果和综合拟合效果吻合。

3 实验验证

为了验证该分布模型的准确性,通过机器人纤维铺放平台进行实验,获得压辊下压量与变形接触长度之间的关系。图8为澳大利亚Monash大学RMRL实验室的机器人纤维铺放平台,通过机械臂与纤维铺方头之间的力/扭矩传感器测量铺放过程中的铺放压力。

图8 机器人纤维铺放平台

该实验使用游标卡尺测量不同压辊下压量时接触区域长度,其结果如图9与表2所示。

图9 压辊下压量与接触长度关系曲线

表2 接触长度LC1与LC2误差

由表2得出,接触长度仿真值LC1与实验值LC2之间的最大误差为5.4%,平均误差为3.2%。同时,通过力/扭矩传感器,能够测得铺放压力与压辊下压量的关系,如图10与表3所示。

表3 铺放压力F1与F2误差

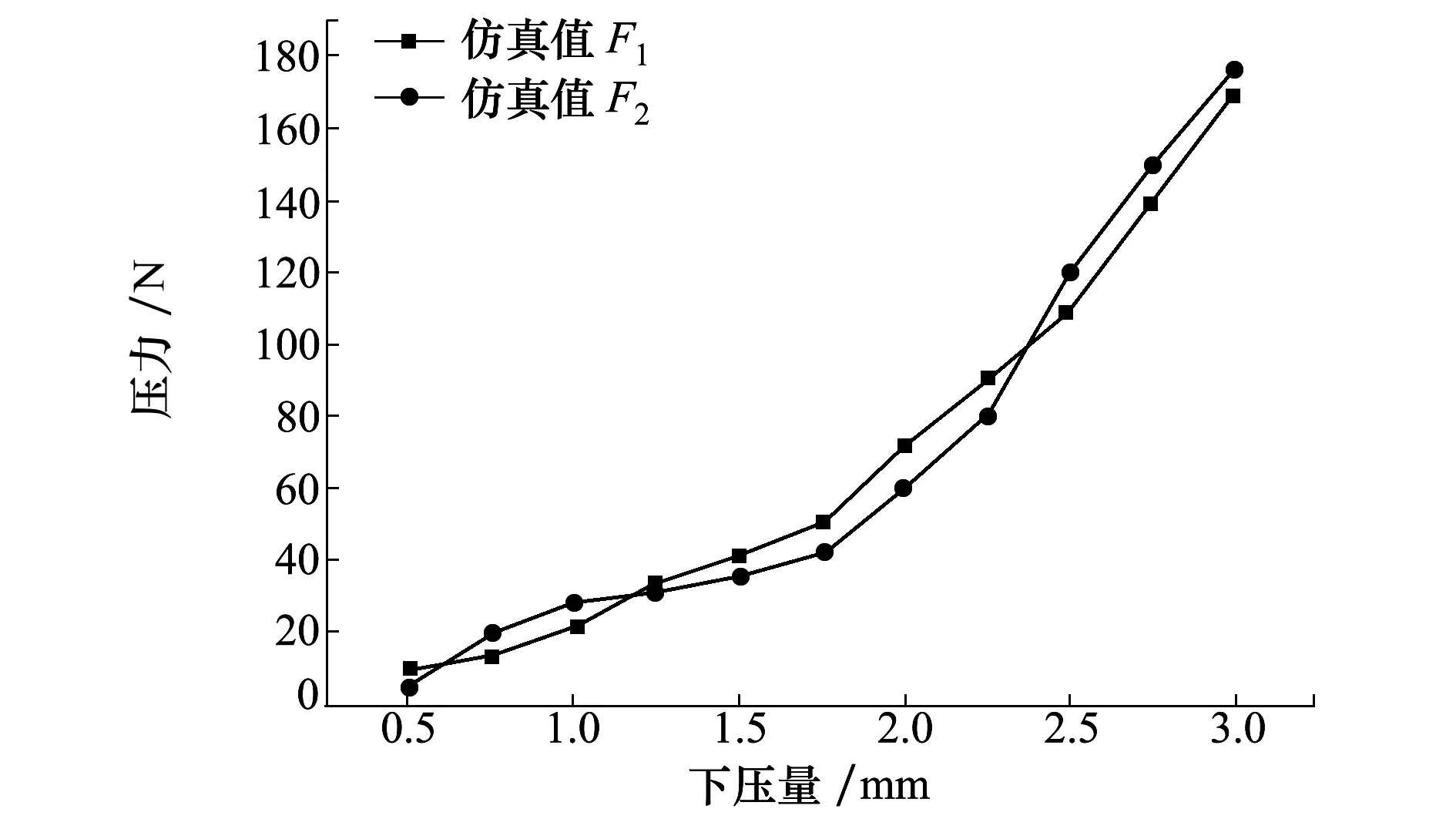
图10 铺放压力与压辊下压量关系曲线

由表3得出,铺放压力仿真值F1与实验值F2之间的最大误差为6.8%,平均误差为4.2%。综上所示,公式(3)表示的压辊变形综合函数模型,能够有效地描绘铺放压应力、压辊下压量与接触区域长度的关系。

4 结 论

针对纤维铺放工艺,分析了压辊变形过程,得出压辊底部的变形不均匀,且压辊与基底芯模接触面上的法向分布也为非均匀分布。基于abaqus对硅橡胶压辊与基体接触过程进行有限元分析研究,建立了压辊压应力分布模型。得出接触压应力、压辊下压量以及压辊与基底的变形接触曲线之间的映射关系,并通过实验得出在不同下压量时,接触长度仿真值LC1与实验值LC2之间的最大误差为5.4%,平均误差为3.2%;铺放压力仿真值F1与实验值F2之间的最大误差为6.8%,平均误差为4.2%。该模型能够有效地描绘铺放压应力、压辊下压量与接触区域长度的关系,为进一步精确控制与优化铺放压力,提高纤维铺放质量奠定了基础。