渗透转化与化归思想培养数学核心素养

颜艳

摘要：转化与化归是指在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化，进而得到解决的一种数学思考方法，其在提升学生的数学解题能力、深化学生的数学思维方面作用显著，是培养与提升学生的高中数学核心素养的重要发力点。因此，文章以在数学教学中培养学生的转化与化归思想为切入点，探讨从多途径、多角度提升学生数学能力与思维的可行策略，真正意义上提升学生数学核心素养的培养，增进学生的综合素质。

关键词：高中数学;转化;化归;数学核心素养

学生核心素养是多维度的，不仅包含知识技能，更加强调能力、情感、态度等多个方面。对于数学学科而言，教师要传授给学生的不仅是数学理论、公式及定理等知识层面的基本技能，还要注重数学思维的形成、数学能力的提升及核心素养的培养，这样才能发挥出数学学科在培养学生的思维及创新能力方面的不可替代的作用。转化与化归思想作为数学思想方法的重要组成部分，需要教师在探析其原则、剖析内容的基础上将这一思想的渗透与培养落实到数学教学的具体环节中去，这样才能全面提升课堂教学的教学质态。

一、 切中肯綮，探析转化与化归的原则

针对学生学习过程中的转化与化归问题，教师要引导学生发现问题的核心与关键，把握问题的本质。为此，探析转化与化归问题的原则，让学生明晰这一类问题的典型特征十分重要。

（一）具体化原则，从抽象到具象

一般来说，转化与化归思想要遵循三个基本原则：熟悉化原则、简单（具体）化原则与和谐化原则。就具体化原则而言，这指的是我们要善于引导学生学会将复杂的、抽象的问题转化为简单的、具象的问题，比如说特殊值法、换元法、降维法、构造法等，都是这一具体化原则的应用。

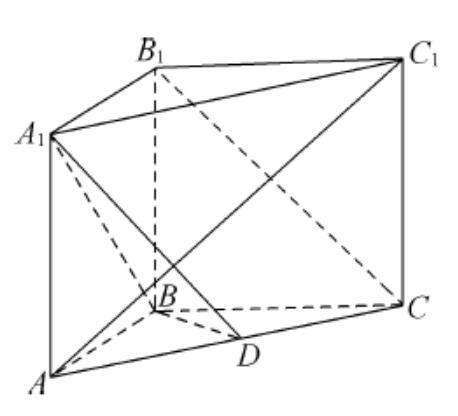
同时，具体化原则也体现在数学知识的教学中。以立体几何的教学来讲，为了让学生学习表面积与体积公式的形成过程，教师就可以利用具体化原则，让学生借助动手实验、制作数学模型的方式，以小组合作的方式，制作简易的圆柱、圆台、三棱锥模型。在这个过程中，学生不仅能归纳总结棱柱、棱锥、棱台的结构特征，认识和理解空间点、线、面的位置关系，也能更直观地了解各几何体的表面积公式以及体积公式的形成过程，具有积极的教学效果。

很多学生在学会一种转化方法之后，很容易出现一味模仿，不知变通，死搬硬套的情况，而出现这种情况的原因很大程度上在于学生并未真正理解转化与化归思想的本质与原则。这也告诫教师在数学课堂渗透转化与化归思想的时候，一定要让学生明确化归的方向，了解转化的原则，这样才能知其然更知其所以然，将被动学习转化为主动学习。

（二）低层次原则，从高维到低维

低层次原则也可以说是具体化原则的另一种表达形式，它体现的是转化与化归过程中高维与低维的转化。从高维到低维不仅是对复杂的数学题目的转化与化归，其本质更是转化学生思考问题的逻辑，深化学生的数学思维，让学生能立足这一基本原则进行有目的的有效化归，寻找有利于问题解决的转化与化归途径。

如已知函数y=sinxcosx+cos2x，求函数的对称轴、对称中心及单调递增/减区间。这是三角函数类型题的普遍形式，但很显然有较高次幂时很难往下求解，这时候就需要学生进行降幂，利用三角恒等变化化简为正弦型函数的最简形式。第一步一定是化简，将二次降为一次，利用三角函数降幂公式进行三角恒等变换，将原函数进行转化，这样才可以带入正弦函数的基本性质，求解其对称中心、对称轴及单调区间。

也就是说，低层次原则的目的是让学生将高维空间的复杂问题转化为低维空间的简化问题。在这个过程中可以将高次数转为低次数，将多元归为低元，问题也就会变得明朗、清晰起来，实现化抽象为具象、化未知为已知、化复杂为简单，最终求得原问题的解，循序渐进地提升学生的高阶数学思维与能力。

二、 条分缕析，探析转化与化归的内容

转化与化归问题，需要厘清问题的关键，让学生在条分缕析中发现知识之间的联系，这不仅能使得知识之间的脉络变得更清晰，更能让学生掌握全面的知识。

（一）数与形转化，拓展解题思路

恩格斯曾说：“数学是研究现实世界的量的关系与空间形式的科学。”可以说“数”与“形”是数学两个最基本的研究对象，也是转化与化归基本对象。因此，数形结合也是渗透转化与化归思想的重要方法。教师要引导学生从数与形的转化角度去思考复杂的数学问题，借助以形助数、以数辅形的手段寻找解决问题的基本思路。

以一道简单的题目来说：已知f（x）=2x（x≥0）

-x2-2x+1（x<0），若函数y=f（x）-m有三个不同的零点，则实数m的取值范围是。

在解这道题的时候，代数的方法非常复杂，需要分多种情况讨论，也很容易出错。但如果我们能够化代数为几何，借助图形进行分析的话就非常简便了。根据题目中的已知信息可以画出函数的基本图像，发现当1

对于数学这门学科而言，解题的过程实质上就是转化的过程。学生可以通过观察、分析、联想、类比等数学思维活动，借助数与形的互化将抽象的数量关系与直观的图形结合起来，实现抽象向具象的转化，针对性地培养与强化转化与化归意识，提升数学解题能力。

（二）正与反转化，寻求最优解法

可逆性是思维的本质属性，思维的可逆性是一种积极的心理活动，对学生思维活动的发展有着积极的影响。因此，教师也要通过在数学课堂中渗透转化与化归思想去培养学生思维的可逆性，让学生善于利用反向思维思考问题，以此来突破思维障碍，拓展解题思路，寻找问题的最优解法。

以一道概率例题来讲：一个袋中装有1红、2白和2黑共5个球，这5个球除颜色外其他都相同，现从袋中任取2个球，则至少取到1个白球的概率为。来看这道题，要是从正向去思考的话可能情况有很多，也比较复杂。但如果用对立事件考慮，把复杂事件分成几个互斥事件的和事件去思考就会简便得多了。“至少一个白球”的对立事件为“没有白球”，则P=1-C23C25=1-310=710。