基于牛顿迭代二值采样信号参数估计的鲁棒算法*

陆敏杰，刘兆霆

(杭州电子科技大学通信工程学院，浙江 杭州 310000)

在诸如目标定位跟踪、系统辨识、语音合成和分析、雷达和声纳信号处理、回归分析等方面，其中的许多问题本质上可以归结为参数估计问题。近年来，由于大规模无线传感器网络(Wireless Sensor Networks，WSNs)的发展，基于WSNs的参数估计成为国内外研究的热点。它利用WSNs末梢大量无线传感器节点收集周围的物理或环境状况(比如温度、声音、振动、压力、运动或污染物等)，并对其进行分析、加工、传输，以实现对感兴趣的物理目标和信息的提取、识别或控制等目的。针对这个问题，国内外已经报道大量的理论研究成果，并探索了在自适应系统[1]、无线通信[2－3]、目标跟踪[4－5]、雷达和声呐[6－7]等方面的相关应用。这些研究成果利用WSNs节点的冗余性提高了信号的空间分集增益，显示出WSNs具有为人们生产生活提供高质量服务的潜能。

然而，无线传感器节点的特点是能量存储、数据处理能力、和通信能力等都十分有限。低比特数据传输和处理有利于节约网络的开支和降低节点的能耗，但这给基于低比特数据且满足性能要求的算法设计带来较大的挑战。目前，国内外学者也已经开展了大量基于WSNs低比特参数估计问题的研究[8－12]。值得注意的是，在实际应用中，某些节点可能处于较为恶劣的环境，其信道容易受到干扰；另外，低比特(单比特)数据本身在传输过程中也很容易受到干扰，这些干扰将导致比特值随机反相。由于这些低比特数据不包含校验位，因此接收端无法判断数据的真实性。直接利用这些数据进行分析会导致现有参数估计算法出现严重偏差。另一方面，信号参数估计问题也常常受到乘性噪声的影响，典型的例子如雷达图像中的散斑噪声、信号传输中的多径干扰等。不同于加性噪声，乘性噪声难以从信号中单独分离出噪声成分，会对估计结果造成很大影响。

针对这个问题，本文讨论了基于WSNs二值测量信号的参数估计问题，研究了在信号加性噪声、二值信道扰动噪声，以及乘性噪声存在情况下的鲁棒估计算法。我们将问题建模为二值变量含误差(Errors-In-Variables，EIV)系统模型的参数估计问题，提出了一种基于极大似然框架下的牛顿法和拟牛顿法。论文推导了参数估计的克拉美罗下界(Cramér-Rao lower bound，CRLB)，并与本文提出算法的估计结果进行了仿真比较，验证了算法具有较快的收敛性和较好的鲁棒性。

1 信号模型

考虑由N个无线节点构成的传感器网络，每个节点能够感知网络环境周围1比特信息yi，i＝1，2，…，N，并且满足下列二值EIV模型:

考虑到网络并非是处于理想环境，节点与处理中心之间的二值传输信道存在随机扰动，导致处理中心接收到的比特信号可能发生反相。也就是说，当第i个节点发送的真实比特信息值为yi＝＋1(或者－1)，而处理中心接收到的信号可能变成了＝－1(或＋1)，它们之间可以表示为如下关系式:

式中，εi∈(1，－1)表示二值干扰噪声。本论文假设存在扰动的差错概率为μ，即P(εi＝－1)＝μ。

论文的目的是在受到乘性噪声ei、加性噪声ni、以及二值噪声εi同时干扰的情况下，利用获得的二值测量值{~yi，i＝1，2，…，N}设计相应的算法，使得处理中心能够提供参数矢量w的有效估计。为了提高在不同环境噪声干扰情况下参数估计的鲁棒性，同时又保证算法具有较快的收敛性，我们分别提出基于极大似然框架下的牛顿和拟牛顿的循环迭代算法。

2 极大似然估计

我们首先将模型(1)等价表示为:

令I＋和I—分别表示事件{i｜yi＝1，i＝1，2，…，N}和事件{i｜yi＝－1，i＝1，2，…，N}的集合，根据式(3)，和P(yi＝－1；，我们可以得到似然函数:

式中，v＝w/σz，y＝[y1，y2，……，yN]T，Φ(u)＝。根据(4)，对数似然函数可以表示为。理想情况下，我们可以通过

获得w的估计；但是实际情况下，从节点到处理中心的二值信道是非理想的，处理中心接收到的数据矢量为~y，它并不完全等于y。如果忽略这一点而仍旧按照(5)直接采用

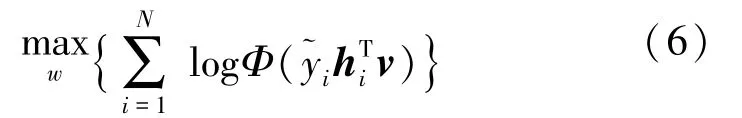
那么相应的估计算法是非鲁棒的，利用该方法获得的参数估计值将出现严重偏差。

因此，不同于式(6)，为了获得更具鲁棒性的算法，我们考虑

注意到，

3 二值牛顿法

假设在第k次迭代后得到的参数估计值为vk，对应的梯度值为gk、Hessian矩阵为Gk，那么第k＋1次迭代后所得到的参数值vk＋1可通过牛顿法更新为:

式中，αk表示搜索步长，符号[·]－1表示矩阵的逆。

值得注意的是，在整个算法迭代的过程中，当搜索步长αk为固定值时，如果αk较大，可能会导致算法无法收敛、计算结果不够理想；如果αk较小，会导致算法收敛速度变得缓慢。为了使每一次迭代的结果更精确，可以通过线性搜索准则来计算出一个较为合适的搜索步长αk，即:

否则将:

式中，δ1和δ2均为给定的参数(0＜δ1＜1，0＜δ2＜1)。在获得vML后，我们可以通过下面的关系式计算wML:

4 二值拟牛顿法

由于Hessian矩阵求逆的运算量大，并且目标函数l(~y；v)的Hessian矩阵的正定性无法保证，从而不能保证搜索方向是下降方向。为了解决这个问题，考虑使用拟牛顿法进行二值信道的参数估计。拟牛顿法利用近似Hessian矩阵的正定逆矩阵计算搜索方向，这既减少了算法的运算量，也保证了搜索方向的正确性。

假设Dk－1为第k－1次迭代循环后的近似Hessian矩阵的逆矩阵(D0设置为p×p的单位矩阵)，vk－1为第k－1次循环得到的参数估计值，gk－1为第k－1次循环的梯度值，那么第k次迭代循环后的近似Hessian矩阵的逆矩阵Dk可以通过下式得到:

式中，Δv＝vk－vk－1，Δg＝gk－gk－1，符号(·)T表示向量的转置。结合Dk，通过二值拟牛顿法获得参数v的更新为

二值拟牛顿法

获取估计值vML后，最后利用式(16)计算出估计值wML。

具体算法步骤总结如下表:

显然，当近似Hessian矩阵Dk由真实的Hessian矩阵Gk的逆矩阵代替时，上述二值拟牛顿算法即为上一节的二值牛顿算法。二值拟牛顿法避免了Hessian矩阵Gk的求逆运算，一般矩阵求逆的运算量级是矩阵维数的3次方，因此二值拟牛顿法比二值牛顿法节省了大约p3量级的运算量。

5 克拉美罗下界(CRLB)

在一定的正则条件下，极大似然估计量的均方误差渐进达到CRLB。因此CRLB为算法的性能提供了一个合理的准则。根据定义，我们可以先计算费歇耳(Fisher)信息矩阵的逆矩阵J:

另外，利用Sherman-Morrison公式[13]，偏导∇vt(v)可以计算为:

式中，H∈ℝp×N为感测矩阵，H＝[h1，h2，…，h3]，符号Λ表示对角矩阵，对角元素

均方误差的CRLB是矩阵J的迹，即CRLB＝tr{[MHΛ(MH)T]－1}。

6 性能测试分析

本节通过MATLAB的性能测试来分析和验证算法的性能，测试数据均通过1 000次的蒙特卡罗平均得到。并且给出了均方误差和克拉美罗下界的实验对比。

不失一般性，假设待估计参数真实值w0＝[－0.5，1.06，0.7]T，加性噪声方差＝0.6，乘性噪声方差＝0.8，传感器个数N＝800。图1比较了分别利用梯度下降算法和牛顿算法得到的均方误差，并且考虑了在理想(μ＝0)和非理想(μ＝0.1)信道两种情况，其中横坐标为算法的迭代次数。可以看出，二值牛顿法比二值梯度下降法收敛速度更快，这一结果也与统计信号处理经典理论是一致的。

图1 二值牛顿法与二值梯度下降法的均方误差与迭代次数的关系对比

图2对比了二值牛顿法与二值梯度下降法的均方误差与传感器个数的关系，设待估计参数真实值w0＝[－0.5，1.06，0.7]T，加性噪声方差＝0.6，乘性噪声方差＝0.8。考虑理想(μ＝0)和非理想(μ＝0.1)信道两种情况，观察图2，发现随着传感器个数的增加，二值牛顿法的收敛速度依旧比二值梯度下降法快，这进一步验证了图1的实验结论。通过对比图2(a)和图2(b)，可以发现在具有扰动的环境下，二值牛顿法具有较好的鲁棒性。

图2 二值牛顿法与二值梯度下降法的均方误差与传感器个数的关系对比

图3对比了基于式(10)得到的鲁棒二值牛顿算法和基于式(6)得到的二值牛顿算法。设置待估计参数真实值w0＝[0.3，0.4，0.5]T，加性噪声方差＝1，乘性噪声方差＝0.3，信道的干扰差错概率μ分别设置为0.1，0.15，0.2。从图3中可以看出在非理想信道环境中，随着传感器个数N的增加，估计值的均方误差逐渐减小；且在相同的干扰差错概率μ下，基于式(10)的鲁棒性二值牛顿算法的均方误差明显小于基于式(6)的非鲁棒性算法的均方误差。前者具有更好的抗干扰能力，其算法精度明显高于后者。

图3 非理想信道下，基于式(6)非鲁棒性二值牛顿法与基于式(10)的鲁棒性二值牛顿法的对比

我们进一步验证乘性噪声和加性噪声对二值牛顿算法的影响。图4(a)的性能测试结果给出了加性噪声固定的情况下，不同的乘性噪声方差对均方误差的影响；而图4(b)给出了在乘性噪声固定的情况下，不同的加性噪声方差对均方误差的影响。该性能测试结果进一步验证了基于式(10)推导的二值牛顿法具有更好的估计性能。

图4 乘性噪声和加性噪声对二值牛顿法的均方误差的影响

图5对比了在不同噪声环境下二值牛顿法和二值拟牛顿法的均方误差以及对应的CRLB。设置扰动差错概率μ＝0.1，待估计参数真实值w0＝[－0.5，0.6，0.7]T。可以看到，当传感器个数N增大时，两种算法的估计值的均方误差都将减小，且均方误差的曲线均逐渐趋向于对应的CRLB曲线。同时从图5也可以看出，随着传感器数量的增加，二值拟牛顿法和二值牛顿法的估计误差逐渐缩小。注意到，二值拟牛顿法避免了Hessian矩阵求逆运算，比二值牛顿法的运算量更低。在本次性能测试中，得到牛顿法的平均时间开销为4.582 88 s，而拟牛顿法的平均时间开销为2.967 44 s。因此，在传感器数量足够多的情况下，我们可以利用二值拟牛顿法代替二值牛顿法。

图5 二值牛顿法与二值拟牛顿法的均方误差和对应的CRLB的对比

7 结束语

本文研究了在乘性噪声环境下，基于传感器网络的二值测量信号的矢量参数估计问题，分别提出了二值牛顿算法和二值拟牛顿算法，并且推导了克拉美罗下界。性能测试结果表明，提出的算法具有较快的收敛性，并且针对传感器节点到处理中心的二值信道存在噪声扰动的非理想情况具有较好的鲁棒性；同时，随着传感器数量的增加，算法的均方估计误差逐渐接近克拉美罗下界。