基于改进Levenberg-Marquardt算法的地磁矢量校准方法*

宋忠国，许丙琳，高久翔，李 婷，张金生，席晓莉

(1.西安理工大学自动化与信息工程学院，陕西 西安 710048；2.火箭军工程大学，陕西 西安 710025)

三轴磁传感器广泛被应用于地磁匹配导航领域进行地磁场矢量测量[1－2]，然而加工工艺限制使得磁传感器存在误差，主要包括非正交误差、灵敏度误差和零偏误差[3－4]，而且安装工艺限制使得磁传感器和其他惯性传感器坐标系之间还存在非对准误差[5]，所以必须校准这些误差才能将三轴磁传感器应用于地磁矢量的高精度测量。

椭球拟合方法是一种常见的标量校准方法[6]，通常需要先利用三轴磁传感器的测量数据求得椭球参数，再通过矩阵分解得到误差校准参数，是一种间接求解误差校准参数的方法。该方法求得椭球参数后只能得到DTD(D为误差校准参数)，虽然可以使用Cholesky分解[7－8]、奇异值分解[6，9－10]等矩阵分解方法从DTD中得到其中的某一个解D1，但是任意旋转矩阵R和D1的乘积RD1依然是校准参数D的解[7，11]，这是因为(RD1)T(RD1)＝D1TRTRD1＝D1TD1，所以椭球拟合方法得到的校准参数会引入一个任意的旋转矩阵R[12]，即椭球拟合法所求解误差校准参数D理论上存在无穷多解。此外，钟浩等人提出使用非线性最小二乘方法[13]直接求解三轴磁传感器误差校准参数，将非正交、灵敏度、零偏误差参数整合为待估计参数，通过Levenberg-Marquard(LM)迭代算法直接求解误差校准参数矩阵D并且无需矩阵分解；罗静博等人提出基于型入侵野草算法校准三轴磁传感器非正交误差[14]也无需矩阵分解。但是这些文献仅仅使用了三轴磁传感器的测量数据进行误差校准，相比于使用更高精度的磁传感器提供地磁场真值参考，这将导致误差校准后三轴磁传感器测量地磁总场的精度偏低，而且这些文献并没有考虑非对准误差，不能获取载体坐标系下地磁场分量信息。李婷等人提出了基于阻尼粒子群优化的地磁场测量误差补偿方法[15]来直接求解误差校准参数并且使用了高精度的质子磁传感器提供地磁场真值，该方法提高了地磁总量校准精度，但仍未考虑非对准误差。总之，为了避免椭球拟合方法需要矩阵分解的弊端和弥补现有直接求解误差校准参数方法在三轴磁传感器测量地磁场总量以及分量上的不足，需要研究新的误差校准方法。

本文提出一种基于改进LM算法的地磁矢量校准方法，首先使用质子磁传感器提供地磁场真值，利用改进LM算法直接求解三轴磁传感器误差校准参数并且无需矩阵分解，然后利用加速度计测量恒定重力场作为辅助信息校准三轴磁传感器和加速度计坐标系之间的非对准误差。通过仿真和实验验证了该方法可以得到加速度计坐标系下高精度地磁矢量。

1 三轴磁传感器误差及非对准误差模型

1.1 三轴磁传感器误差模型

根据误差产生机理的不同，三轴磁传感器误差主要分为3类:非正交误差、灵敏度误差、零偏误差。

①非正交误差

非正交误差是指由于三轴磁传感器工艺制造水平的影响，三个测量轴无法保证两两正交，从而引起的测量误差，其几何定义如图1所示。

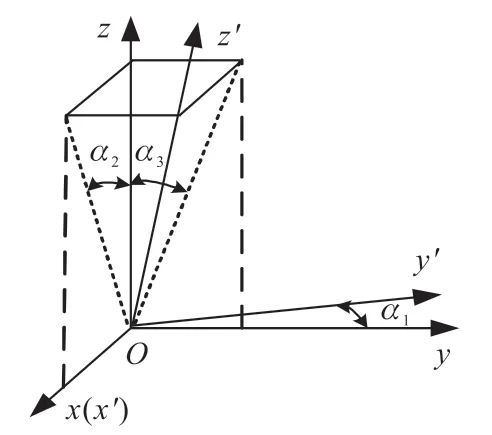
图1 非正交误差

假设xyz坐标轴构成的坐标系为三轴磁传感器理想正交坐标系，而x′y′z′坐标轴构成的坐标系为实际情况下的非正交坐标系。将两套坐标系的坐标原点重合、x坐标轴和x′坐标轴重合，y坐标轴和y′坐标轴共面，可以得到非正交误差角(α1α2α3)。理想正交坐标系和实际非正交坐标系之间的非正交误差可以等效为矩阵O，其数学模型可以表示为:

②灵敏度误差

灵敏度误差是指由于三个测量轴各自的灵敏度不能做到完全一致、测量信号的放大电路特性不完全相同，从而引起的测量误差。

③零偏误差

零偏误差是指实际使用过程中磁传感器各个测量轴、模拟调理电路、A/D转换的零点不为零所带来的测量误差。

灵敏度误差K和零偏误差b的数学模型如下所示，其中Kx、Ky、Kz以及bx、by、bz分别代表三轴磁传感器x、y、z三个测量轴各自不同的灵敏度和零偏。

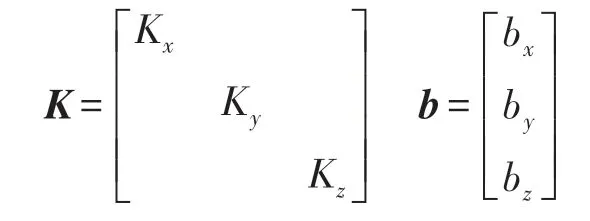
式中，n为实际测量时的高阶噪声。

令C＝b＋n，则误差模型可以整理为:

那么有(3)成立:

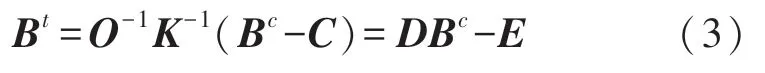
式中，D和E称为误差校准参数，求出后即可得到三轴磁传感器坐标系下的地磁场矢量Bt。

1.2 非对准误差模型

由于安装工艺限制，三轴磁传感器坐标系和加速度计坐标系或其他惯性坐标系之间还存在坐标系非对准误差，只有校准该误差才能将Bt投影至加速度计或其他惯性坐标系下，从而提高加速度计坐标系下或其他惯性坐标系下地磁场矢量测量精度。

本文考虑了三轴磁传感器坐标系和加速度计坐标系之间的非对准误差。非对准误差可以等价为一个正交旋转矩阵Rm，设xyz坐标系为三轴磁传感器正交坐标系，x2y2z2坐标系为加速度计正交坐标系，xyz坐标系到x2y2z2坐标系转换所需的旋转欧拉角为(u1u2u3)，其几何定义如图2所示，则Rm的数学模型可以表示为式。

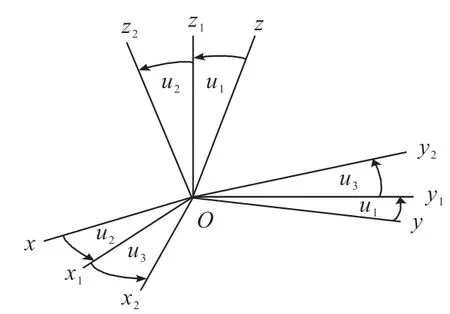
图2 xyz坐标系到x2y2z2坐标系的变换

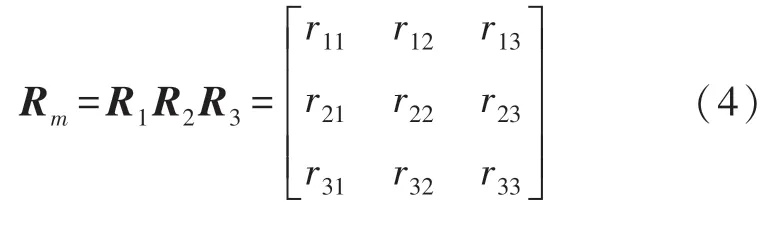
式中，

求得Rm即可得到加速度计坐标系下的地磁场矢量。

2 基于改进LM算法的三轴磁传感器校准方法

求解三轴磁传感器误差校准参数的问题可以被视为非线性最小二乘参数估计问题，本节首先建立目标函数模型，再通过改进LM算法直接求解误差校准参数，且无需矩阵分解。

2.1 非线性最小二乘目标函数构建

理想情况下三轴磁传感器测量的地磁总场值Bt可以表示为:

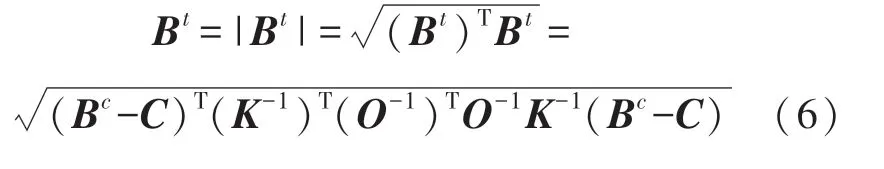
式中，

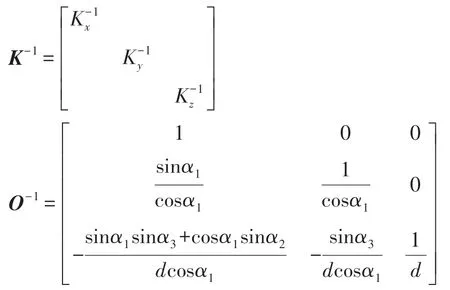
将质子磁传感器测量地磁总场值BM作为地磁总场的真实值，那么求解三轴磁传感器误差校准参数的非线性最小二乘问题可以表示为式:

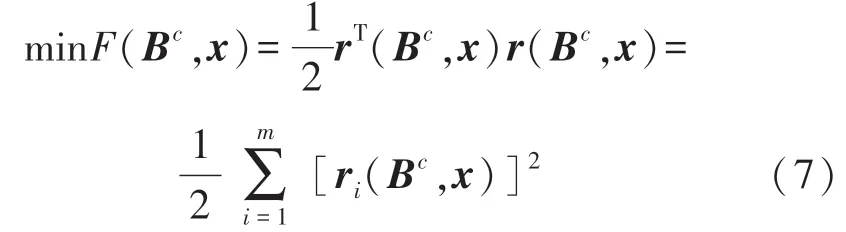
式中，F(Bc，x)为目标函数。

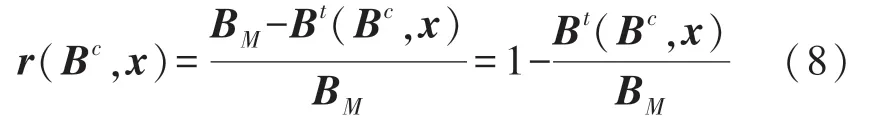
式中，r(Bc，x)为残差函数，采用三轴磁传感器测量的地磁总场Bt和地磁总场真实值BM之间的相对误差来表示，描述了误差校准后Bt相对于真值BM的偏差程度。待估计参数向量为x＝[bxbybzKxKyKzα1α2α3]，它包含了三轴磁传感器零偏误差、灵敏度误差以及非正交误差模型中的9个参数。

采用Bt相对于BM的相对误差作为残差函数，以最小二乘为准则，通过非线性最小二乘方法求解误差校准参数可以使得三轴磁传感器的总量输出尽可能地逼近质子磁传感器的输出。这种方法的好处:非线性最小二乘方法求得估计参数x后可以根据1.1节中的误差模型直接得到灵敏度误差矩阵K、非正交误差矩阵O以及零偏向量b，无需矩阵分解便可以由式得到三轴磁传感器误差校准参数矩阵D和E。这样不仅可以避免椭球拟合方法矩阵分解时引入任意旋转矩阵R的问题，而且由于使用了更高精度的质子磁传感器作为了校准参考，误差校准后三轴磁传感器在地磁场总量测量方面的精度会更高。

2.2 改进的LM算法

本文使用的LM算法是牛顿高斯法和最陡下降法相结合的一种算法，其保留了两者各自的优越性。LM算法的传统迭代形式为式(9)，当λ较大时，式(9)退化为最陡下降法，在距极值点较远的位置具有较大的下降速度，而当λ较小时，式(9)退化为牛顿高斯法，在极值点附近也能快速收敛。

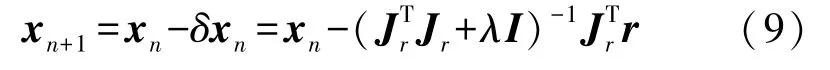
改进的LM算法迭代形式如式(10)所示:

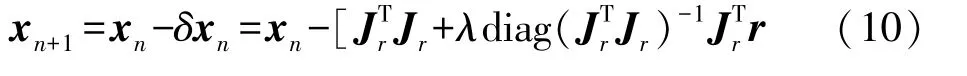
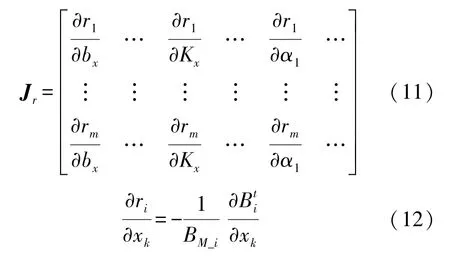
式(11)中:Jr(m×9)为残差函数r的雅可比矩阵，m为采集数据量的个数，9为待估计参数个数，式(12)为Jr中元素的一般表达形式；为目标函数F的梯度，r(m×1)为m个测量数据对应的残差向量；代替了二阶偏导数构成的黑塞矩阵；λ为阻尼因子。

3 非对准误差校准原理

经改进LM算法校准三轴磁传感器误差后，即可得到三轴磁传感器坐标系下高精度地磁场矢量Bt，由于并未使用矩阵分解，Bt中不会引入任意旋转矩阵，这将在校准非对准误差时避免任意旋转矩阵所带来的影响。由于矩阵分解会引入旋转矩阵，求解的非对准误差参数将是安装工艺带来的坐标系旋转和矩阵分解引入的坐标系旋转二者叠加的参数，此时矢量校准精度较低。此外，当矩阵分解时引入的旋转矩阵所对应的旋转欧拉角较大时，将无法再利用重力场测量数据作为辅助使得三轴磁传感器测量的地磁场投影到加速度计坐标系上。

式中，G＝[gxgygz]T为重力场G对应的单位矢量，为对应的单位矢量，Bt＝[bxbybz]T为Bt对应的单位矢量，使用最小二乘参数拟合法即可求解式(13)中非对准误差矩阵Rm，将Rm代入式(5)中即可得到加速度坐标系下的高精度地磁场矢量。

4 数值仿真验证

首先，模拟理想情况下三轴磁传感器采集的地磁场矢量信号Bt，其总量真实值由模拟的质子磁传感器测量值提供；其次，加入预先设置的非正交、灵敏度、零偏和非对准误差以及随机测量噪声，得到三轴磁传感器实际工作情况下测量的地磁场信号Bc；最后对本文提出的基于改进LM算法的地磁矢量校准方法进行验证并分析校准效果。

预先设置的非正交误差角为(1° 1.5° 2°)，则非正交误差O如下所示:

预设的灵敏度误差K，零偏误差b(单位nT)为:

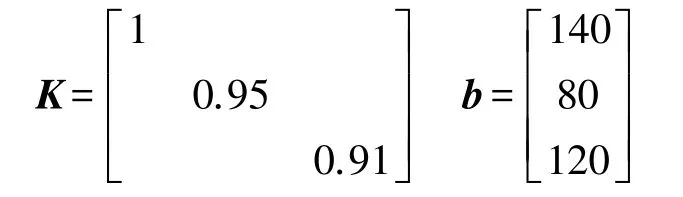
将上述预设的误差模型代入式中可以得到误差校准参数D和E的真实值:

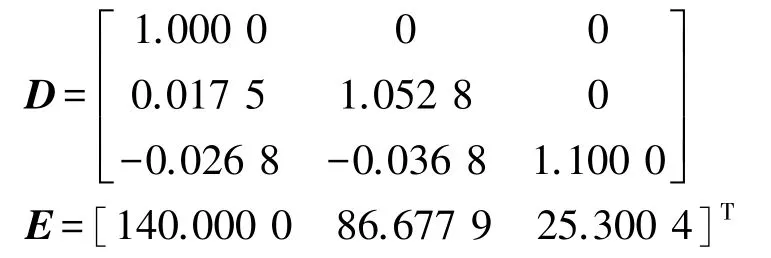
模拟质子磁传感器测量的地磁总场真实值BM为52 590 nT，模拟测量噪声n为信噪比60 dB的高斯白噪声。预先设置的三轴磁传感器坐标系和加速度计坐标系之间非对准旋转欧拉角为(1°0.5°1.5°)，重力矢量G取[0 0 9.8]T。三轴磁传感器和加速度计经过模拟姿态变换可以得到不同姿态下的测量数据Bc和G。

将模拟的三轴磁传感器测量数据Bc和质子磁传感器测量的地磁场真值BM代入下述LM算法迭代步骤中，分别采用2.2节描述的两种LM算法迭代形式均可以求得x参数的估计值＾x，两种迭代形式的结果对比分别如表1、表2所示(表中α1、α2、α3为其弧度制表示，单位为rad)，表明使用改进LM算法求出＾x的误差更小。

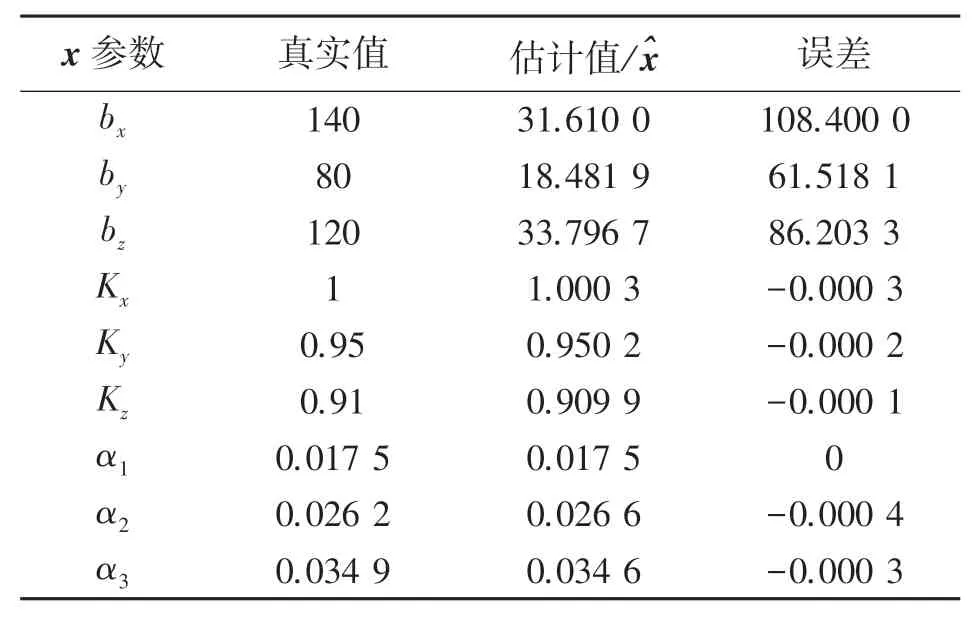
表1 基于传统LM算法x参数估计结果

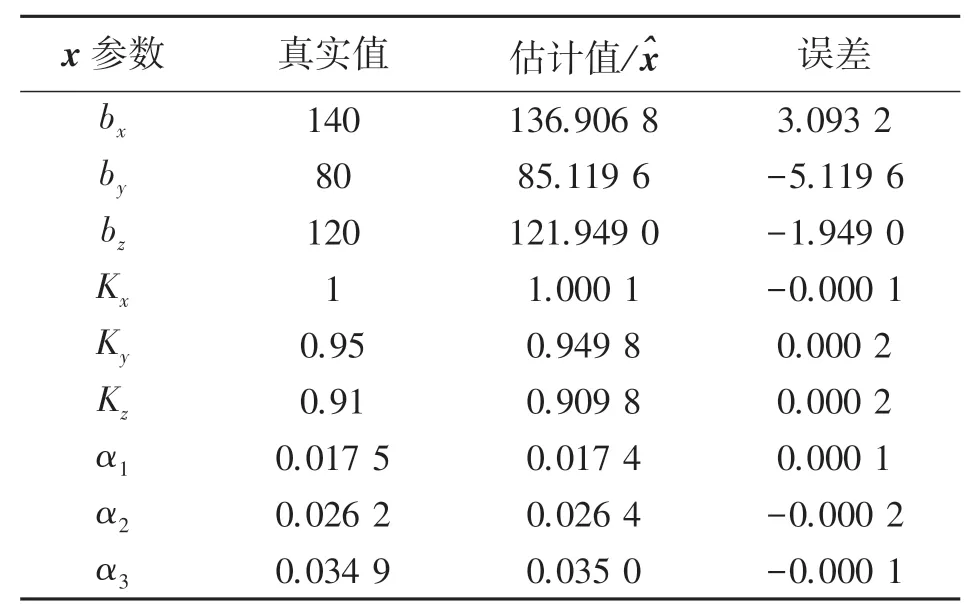
表2 基于改进LM算法x参数估计结果

LM算法迭代求解待估计参数x的步骤如下:

①初始迭代次数n＝1，待估计参数向量x初始值x0＝[0 0 0 1 1 1 0 0 0](K－1中分母不能为0，这里取1)，阻尼因子初始值λ0＝0.01；

③若‖rn＋1‖2≤‖rn‖2，则λn＋1＝λn/10，否则，λn＋1＝10λn，转(4)；

④迭代次数n＝n＋1，更新，更新δxn，返回②。

使用改进LM算法求解出后代入第1.1节中的误差模型中，可以得到校准参数D和E的估计值和，其与真实值相比差距很小，将和代入式(3)即可实现三轴磁传感器误差校准。

校准三轴磁传感器误差后，残差r的频数分布直方图如图3所示，该频数分布满足均值为0的高斯分布，红色曲线为对应的高斯分布曲线，这符合测量噪声为高斯分布的预设。

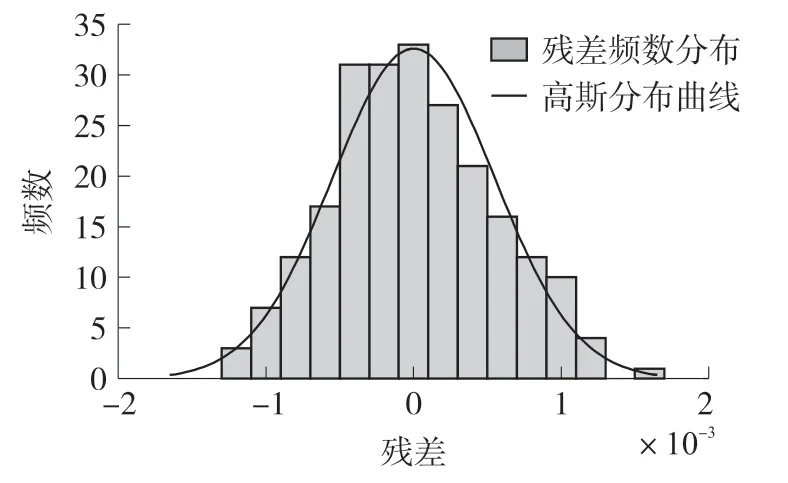
图3 残差频数分布直方图

三轴磁传感器误差校准前后测量地磁总场对比如图4所示，误差校准后的绝对误差如图5所示。经过分析，校准前，地磁总场测量误差较大，均方根误差为2 813.9 nT，校准后，误差大幅度减小，均方根误差减小至29.8 nT。

图4 校准前后地磁场总量

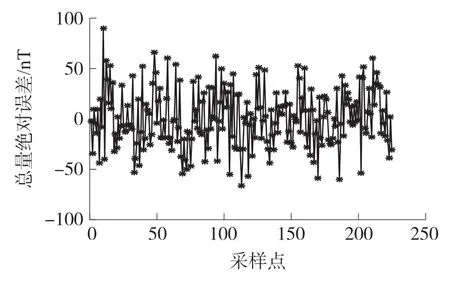
图5 校准后地磁场总量绝对误差

由预设的旋转欧拉角可以得到非对准误差参数的真实值Rm，而利用校准磁传感器误差后得到的地磁场矢量Bt和重力矢量测量值G，并根据第3节非对准误差校准原理可以求得Rm的估计值，将其代入式(5)即可得到加速度坐标系下的地磁场矢量。

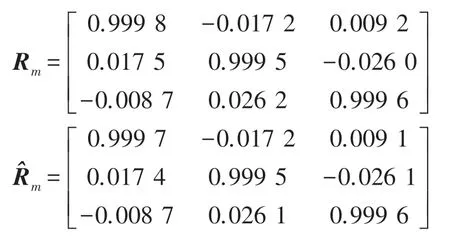
图6为非对准误差校准前后三轴磁传感器测量地磁场分量的绝对误差。非对准误差校准前加速度计坐标系下X轴、Y轴、Z轴地磁场分量的均方根误差分别为:583.7 nT、580.1 nT、582.3 nT，误差校准后，三分量的均方根误差分别为:28.3 nT、29.6 nT、34.1 nT。

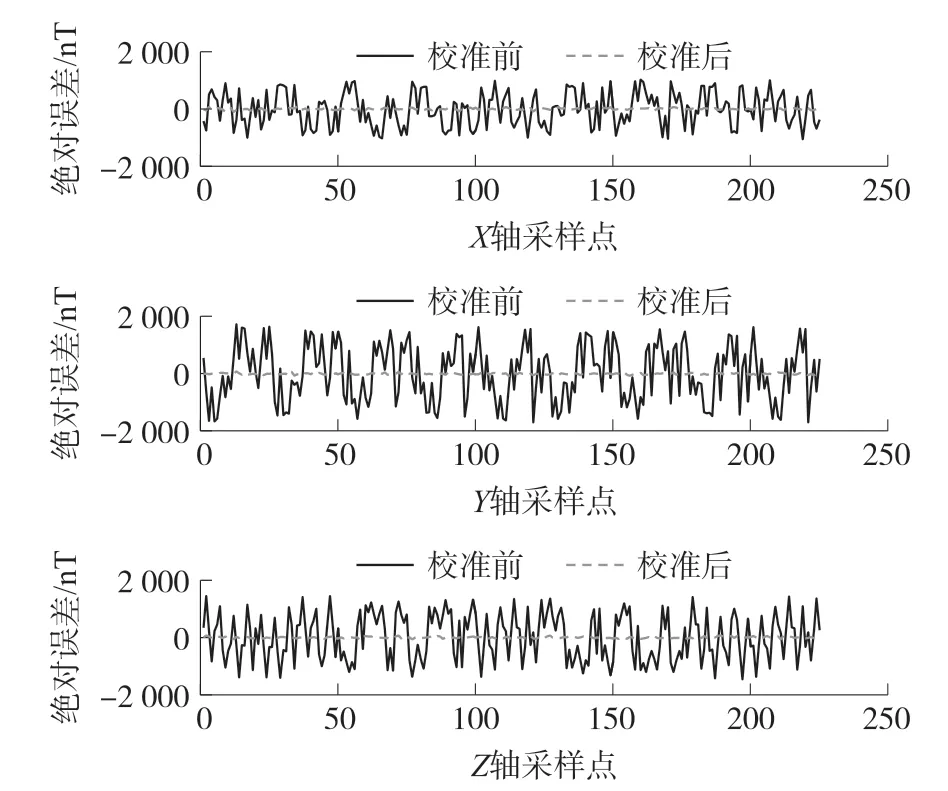
图6 校准前后分量绝对误差

5 实验结果分析

在西安理工大学金花校区远离建筑物的操场中心位置处进行实验，验证基于改进LM算法的地磁矢量校准方法的有效性。实验过程中使用的三轴磁传感器为MS－03A型磁通门磁传感器；使用GSM－19 Overhauser质子磁传感器提供地磁场真值。将三轴磁传感器以及加速度计模块(模块外壳使用无磁的铝合金材料)放置在无磁转台上对地磁场和重力场进行测量，实验系统示意图如图7所示，各个实验设备及实验操作如图8所示。

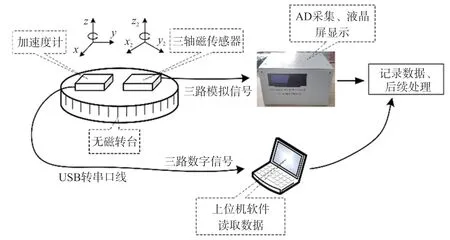
图7 实验系统示意图

图8 实验设备与实验操作示意图

首先在操场中心位置使用质子磁传感器测量地磁场的真实值并取平均，得到该位置处的地磁场真实值大小为52 260 nT，然后在相同位置放置支架、无磁转台并固定磁通门磁传感器，分别将磁传感器的X轴(＋/－)、Y(＋/－)轴向上和向下，每隔15°旋转一次转台获取实验数据，每个点测量两次并取其平均值。

图9为实验数据验证改进LM算法校准三轴磁传感器误差前后测量地磁总场的对比图。经过分析，误差校准前测量地磁总场的误差较大，校准前地磁场总量均方根误差为693.1 nT，校准后均方根误差降为184.9 nT。

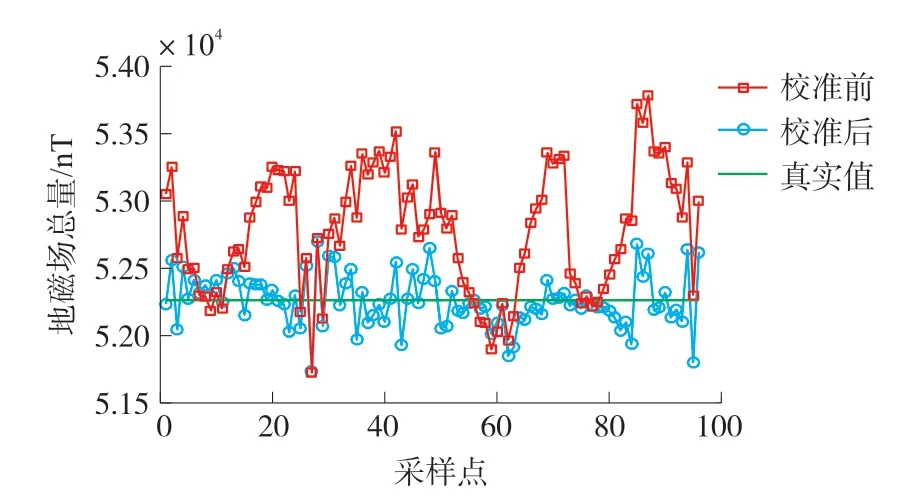
图9 校准前后地磁场总量

非对准误差造成的地磁场分量误差可以通过航向角误差来反映。图10为校准非对准误差前后航向角绝对误差，经过分析，非对准误差校准前航向角均方根误差为17.2°，而校准非对准误差后航向角均方根误差降至2.2°，这证明该方法得到了加速度计坐标系下高精度地磁场矢量。

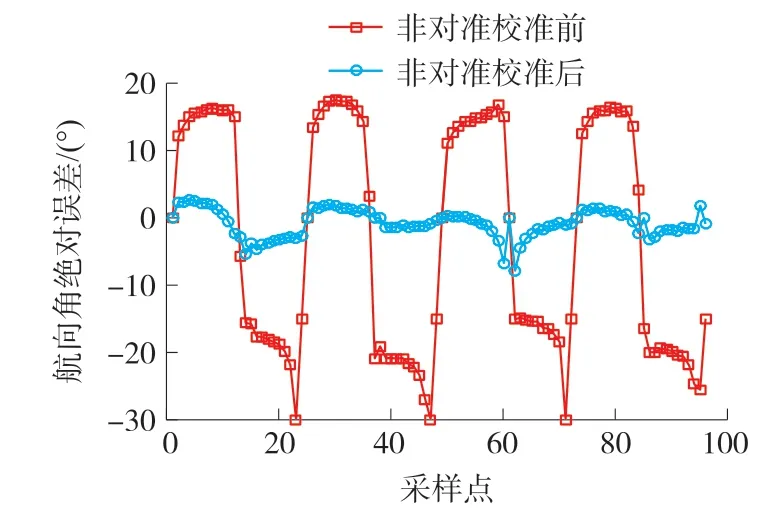
图10 非对准误差校准前后航向角绝对误差

6 总结

本文提出了一种基于改进LM算法的地磁矢量校准方法，首先使用改进LM算法直接求解三轴磁传感器误差参数，避免了椭球拟合方法因矩阵分解引入任意旋转矩阵的问题；然后校准了三轴磁传感器和加速度计坐标系之间的非对准误差。仿真结果表明，基于改进LM算法的矢量校准方法可使地磁总场的均方根误差减小两个数量级，分量精度提高一个数量级；实验结果表明本文所提方法能够大大提高三轴磁传感器测量精度，最终获得了加速度计坐标系下的高精度地磁场矢量。