基于改进MVO和WLSSVM的燃煤锅炉NOx排放优化

梁 涛，靳云杰，姜 文，刘子豪

(1. 河北工业大学人工智能与数据科学学院，天津 300130; 2. 河北建投能源投资股份有限公司，河北 石家庄 050011)

0 引 言

随着经济快速发展，火电厂的燃煤消耗量逐年增加，伴随而来的是NOx的排放量越来越多。NOx易形成酸雨和光化学烟雾，不仅污染环境而且会造成一定的经济损失[1]。因此，降低NOx排放量是电厂面临的重要课题。

目前国内的电站燃烧运行主要由运行人员根据自己的工程经验进行燃烧调整，但是由于锅炉燃烧的复杂性，此种方法费时费力而且优化效果不太理想。近年来随着机器学习与智能算法的不断发展，为锅炉燃烧优化提供了一种新的方向。通过建立一个精确的锅炉燃烧系统模型[2]，并以此模型为基础，通过智能算法优化锅炉运行时的可调参数，给出可调参数的最佳值，可以实现锅炉的清洁高效运行，降低锅炉运行过程中的NOx排放量。

人工神经网络（artificial neural networks,ANN）作为当前比较热门的一个研究方向，已被许多学者成功应用于燃煤锅炉NOx排放量的预测和优化[3]。但是人工神经网络也存在着一些缺点，例如训练过程需要大量的样本数据，并且容易出现过度拟合的问题。支持向量机[4]（support vector machine,SVM）是一种根据统计学习理论，以结构风险最小化原则为基础的机器学习方法，因其具有结构简单、泛化能力强的优点，有效解决了神经网络训练过程中出现的过拟合问题，所以被广泛应用于故障诊断[5]、缺陷检测[6]等工程领域。然而，由于SVM在训练样本增多时会导致其计算量急剧增加，影响其建模的效率。Suykens等[7]提出的最小二乘支持向量机（least squares support vector machine，LSSVM）将问题归结为线性方程组，采用等式约束代替不等式约束，避免了求解二次回归问题，减少了计算复杂性。文献[8]构建了一个基于LSSVM的集成学习系统，以预测燃煤锅炉的NOx排放。文献[9]采用差分进化算法来优化LSSVM参数，并构建NOx排放量预测模型。文献[10]采用最小二乘支持向量机建立电站锅炉燃烧模型，然后利用遗传算法对锅炉运行工况进行寻优，为锅炉运行过程提供最佳的操作变量设定值。

然而，LSSVM算法也存在鲁棒性不足等问题，为此，Suykens等[11]提出一种加权最小二乘支持向量机（weighted least squares support vector machine,WLSSVM）算法，依据训练样本的拟合误差分别赋予其不同的权重，减少了噪声的影响，大大提高了LSSVM算法的鲁棒性。

基于上述研究分析，本文首先采用IMVO算法对WLSSVM的模型参数进行寻优，建立基于IMVOWLSSVM的燃煤锅炉NOx排放量预测模型。然后在该预测模型的基础上，采用IMVO算法对燃煤锅炉运行可调参数进行寻优，以降低锅炉运行时的NOx排放浓度。

1 改进多元宇宙算法

1.1 多元宇宙算法

多元宇宙优化算法（multi-verse optimizer,MVO）是基于多元宇宙理论中的白洞、黑洞、虫洞相互作用现象启发而得到的智能优化算法[12]。黑洞是已发现的天体，它会吸收宇宙中所有的物体；白洞则与黑洞正好相反，它是一个只发射不吸收的特殊天体；虫洞是连接黑洞与白洞的多维时间隧道。而多元宇宙则通过黑洞、白洞与虫洞三者之间的相互作用达到一个稳定的状态[13]。

MVO算法的具体描述如下：

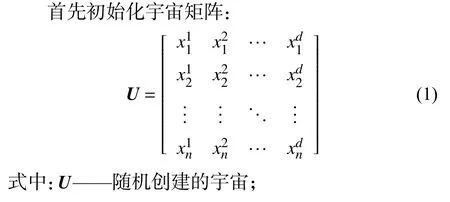
1.2 改进多元宇宙优化算法

在多元宇宙优化算法中，虫洞存在概率 W EP和虫洞旅行距离率TDR是影响算法优化效果的两个重要参数，W EP和TDR的变化趋势曲线图如图1所示。

图1 WEP和TDR的变化曲线

因为多元宇宙需要通过虫洞的随机性来保证宇宙的稳定性和多样性，所以一个合适的旅行距离率TDR可以提升MVO算法的性能，更容易找到最优的个体，提升全局寻优能力[14]。针对TDR值下降速度较慢而导致旅行距离增加的问题，提出一种改进的多元宇宙优化算法，将TDR值以指数函数方式下降，增大其下降速度，此时IMVO的TDR计算公式为：

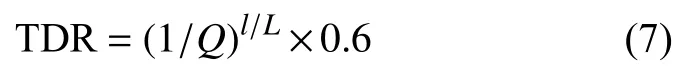
其中，Q为常数，在本文中取5000。

改进后的MVO流程如图2所示。

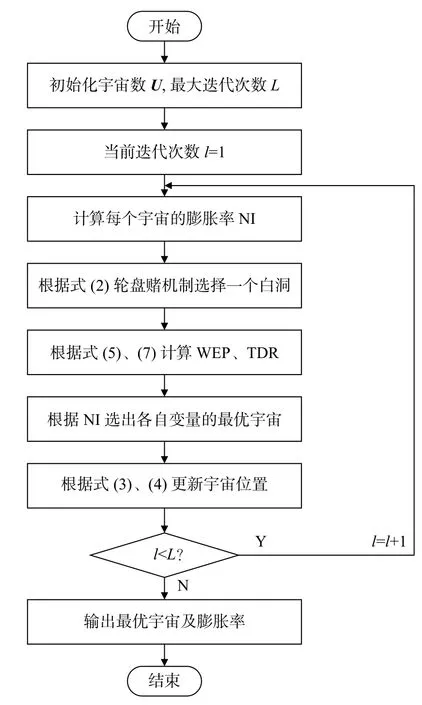
图2 改进MVO流程图

2 基于改进MVO算法优化的WLSSVM预测模型

2.1 加权最小二乘支持向量机算法

2.2 改进MVO算法优化WLSSVM参数

模型的正则化参数C和核参数 σ 的选取对WLSSVM模型的鲁棒性与泛化能力有很大的影响，所以本文采用改进的MVO算法来对WLSSVM模型的C和 σ进行优化和选择，提升模型的预测效果。

IMVO算法优化WLSSVM模型参数的具体步骤为：

1)为了消除数据集不同属性间的差异，将采集到的样本数据进行归一化处理。

2)选定WLSSVM模型的训练集与测试集。

3)确定正则化参数C和核参数 σ的取值范围，设置IMVO的最大迭代次数L，宇宙个数U。

4)初始化宇宙位置，每个宇宙跟宇宙中的个体对应一个二维向量 (C,σ)。

5)计算每个宇宙的膨胀率并根据式(2)轮盘赌机制选择一个白洞。

6)根据式(5)和式(7)计算虫洞存在概率和虫洞旅行距离率 T DR。

7)计算当前宇宙膨胀率，若宇宙膨胀率优于当前宇宙膨胀率，则更新当前宇宙膨胀率，否则保持当前宇宙。

8)更新式(3)和式(4)更新宇宙位置。

9)判断当前是否满足终止条件(到达足够好的宇宙或者达到最大迭代次数)，如果满足，则程序终止，并输出最优的一组解 (C,σ)，否则迭代次数加1，转步骤5)继续搜索。

基于IMVO-WLSSVM的NOx排放量预测模型如图3所示，该模型主要包括数据预处理、IMVO参数寻优及模型预测。

图3 NOx排放量预测模型示意图

3 实例分析

3.1 样本数据选取

本文以某电厂实际运行的 330 MW机组燃煤锅炉为研究对象，选取230组锅炉运行数据作为总样本。从总样本中选取150组数据作为训练样本，训练预测模型，80组数据作为测试样本，检验模型的泛化能力。

每一组样本数据都包括17维参数，前16维为本文选取的对NOx排放量影响较大的锅炉运行参数，包括锅炉负荷、排烟温度、烟气含氧量、给煤量、一次风量、二次风量、燃尽风量，第17维为锅炉的NOx排放量，具体锅炉运行数据见表1。

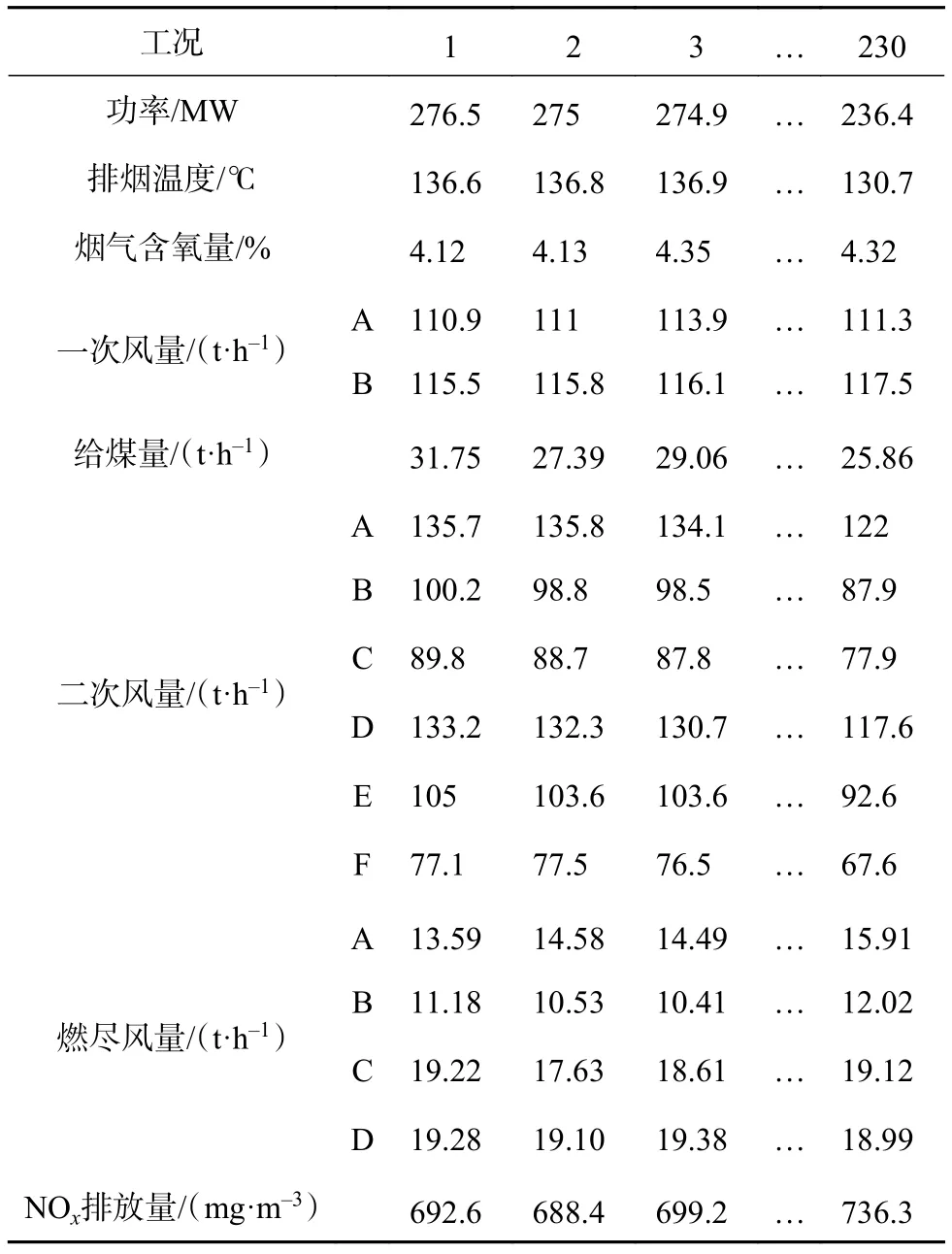
表1 锅炉运行数据

3.2 模型训练

以每组数据的1～16维作为模型的输入，NOx排放量作为模型的输出，建立IMVO-WLSSVM预测模型，同时建立GA-WLSSVM以及MVO-WLSSVM模型，用来比较模型的预测效果。其中IMVO算法的参数设置为：宇宙数U=5，最大迭代次数L=100；MVO算法的参数设置与IMVO算法相同；遗传算法(GA)的参数设置为：交叉概率为0.7，变异概率为0.2。

经过IMVO算法对WLSSVM模型进行寻优以后，WLSSVM模型的最佳正则化参数C和最佳核参数 σ 分别为 11.3137、0.1250，然后根据得到的参数对预测样本进行预测。三类模型的预测结果如图4所示。

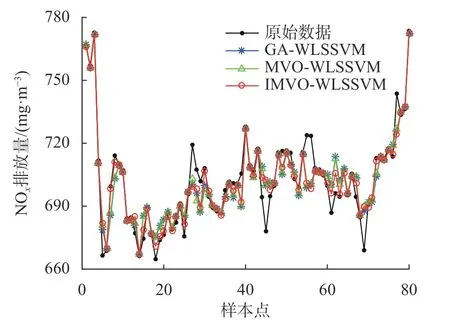
图4 3种模型的预测结果

从图4可以看出，这三类模型的预测结果都在一定程度上较好地跟随了NOx排放量的变化趋势。与其他两种模型相比，IMVO-WLSSVM模型通过IMVO算法对WLSSVM模型的参数寻优，有效地减小了预测误差，提高了模型的预测精度，也证明了相比于遗传算法和原始的多元宇宙算法，改进后的多元宇宙算法具有更好的寻优能力。

3.3 预测结果分析

为了进一步比较模型的预测效果，本文使用平均绝对误差 (average absolute error，MAE)、平均绝对百分比误差 (average absolute percentage error，MAPE)和均方根误差 (root mean square error，RMSE)作为评价指标，对模型的预测效果进行评价。MAE、MAPE及RMSE的定义如下：

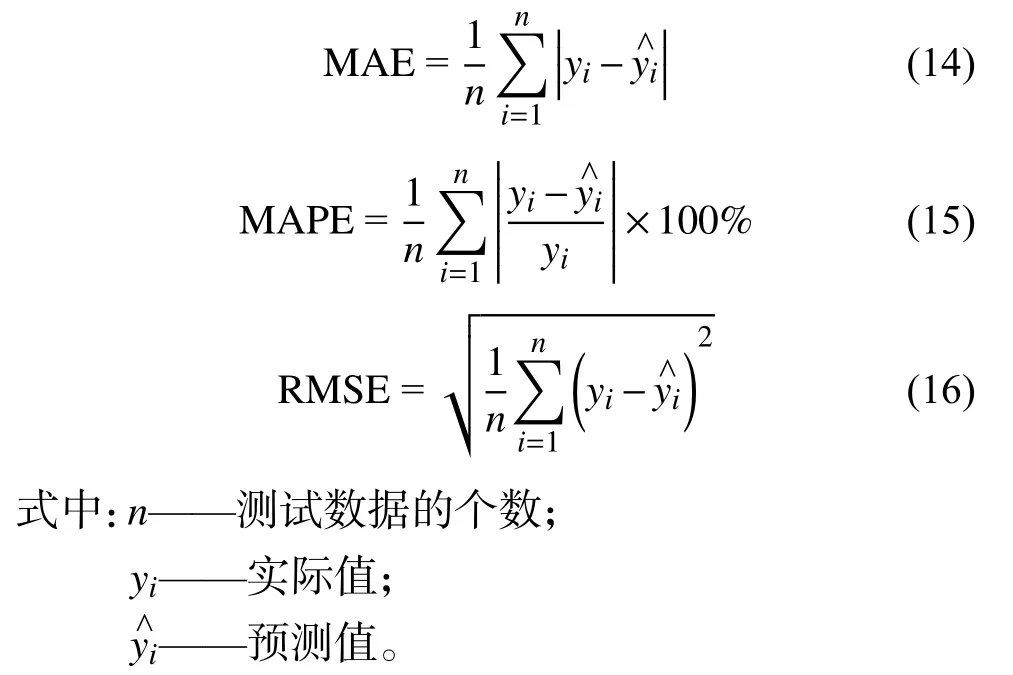
表2给出了3种模型的预测效果评价指标的计算结果。

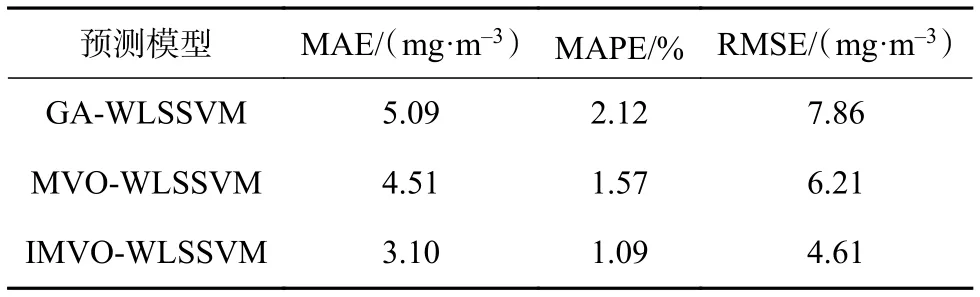
表2 3种模型的预测性能比较

从图4和表2可以看出，IMVO-WLSSVM预测模型的平均绝对误差、平均绝对百分比误差、均方根误差三者均优于GA-WLSSVM及MVO-WLSSVM预测模型。结果表明所建IMVO-WLSSVM模型预测误差最小，预测精度最高，可以有效地提升燃煤锅炉NOx排放量的预测效果。

4 NOx排放量优化

本文在上节所建的NOx排放量预测模型的基础上，采用IMVO算法对锅炉运行可调参数进行寻优，获得最优的锅炉运行可调参数组合，达到降低锅炉燃烧所产生的NOx排放量的目的。具体的优化流程如图5所示。

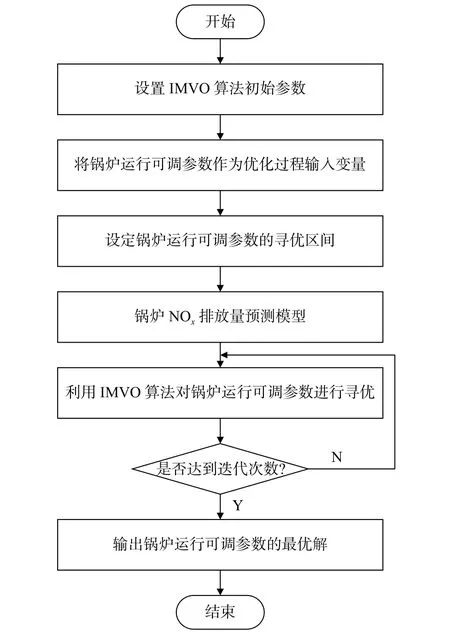
图5 锅炉优化流程图

在优化过程中，锅炉运行可调参数包括烟气含氧量、2个一次风量、给煤量、6个二次风量、4个燃尽风量，将以上14个参数作为优化变量进行寻优，剩余的不可调变量在寻优过程中作为固定值保持不变。将14个锅炉运行可调参数定义为一个待优化变量x，则有：

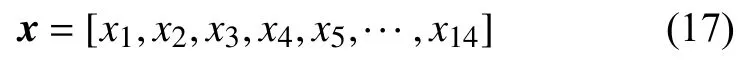
式中：x1——烟气含氧量；

x2,x3——2个一次风量；

x4——给煤量；

x5～x10——6个二次风量；

x11～x14——4个燃尽风量。

根据现场采集的实际锅炉运行数据的最大值跟最小值确认14个优化参数的寻优区间，各个参数的寻优区间见表3。

表3 各个优化参数的寻优区间

优化的目标为降低锅炉运行中产生的NOx排放浓度，优化目标的数学描述为：

其中fNOx(x)为锅炉NOx的排放浓度。

从锅炉运行样本数据中随机选取样本15，采用IMVO算法对锅炉运行可调参数进行寻优，以降低锅炉的NOx排放浓度。

为了验证IMVO算法的优化效果，同时利用MVO算法对样本15进行参数寻优。两种优化算法的参数设置相同，宇宙数为10，最大迭代次数为100。经过寻优以后，将得到的NOx排放浓度最小值作为最优值，根据其对应的解确定各个优化参数的最优值。IMVO、MVO两种算法对样本15的寻优过程见图6，具体的优化结果见表4。

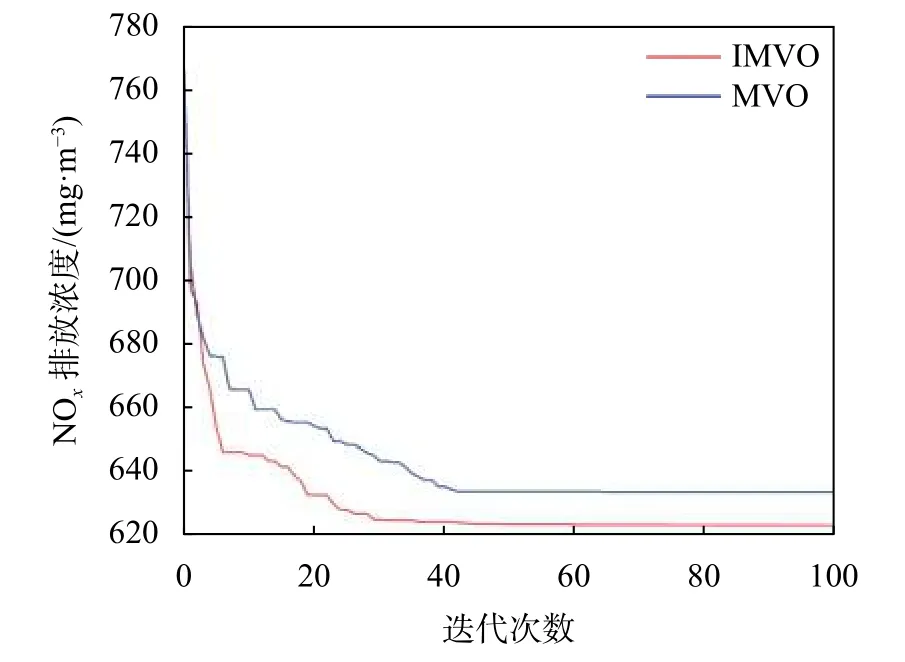
图6 两种算法对样本15的优化过程

表4 两种优化算法的优化结果

由图6可以看出随着迭代次数的增加，NOx排放量也在随之逐渐下降，并最终趋于稳定。在寻优过程中，IMVO算法所需的迭代次数少于MVO算法，证明改进后的多元宇宙算法具有更快的寻优速度。由表4可以看出，相对于原始数据，两种优化算法优化后的NOx排放浓度均有了一定程度的下降，相对于MVO算法，IMVO算法寻优后的下降幅度更为明显，证明改进后的多元宇宙算法具有更好的寻优效果。

同时为了对比IMVO算法的实用性，分别使用IMVO算法与MVO算法对样本20到样本30共11组样本数据进行寻优。寻优结果见表5。由表可以看出，IMVO算法与MVO算法的NOx排放浓度平均减少量分别为 150 mg/m3和 120 mg/m3，每组样本优化平均耗时分别为为20 s和35 s，证明改进后的多元宇宙算法在连续寻优时具有更快的寻优速度、更好的寻优效果以及更强的实用性。

表5 两种优化算法的优化性能比较

5 结束语

为了降低电厂燃煤锅炉的NOx排放浓度，本文首先采用一种基于改进多元宇宙优化算法与加权最小二乘向量机相结合的建模方法来建立NOx排放量预测模型，该模型采用IMVO算法对WLSSVM的模型参数进行寻优，进一步提高了模型的预测精度。将该预测模型应用于某电厂330 MW燃煤锅炉，并与其他模型的预测效果进行对比分析，结果表明，IMVO-WLSSVM模型各项指标均优于其他模型，能够较好地预测NOx排放量，具有较高的预测精度与良好的泛化性。然后在该NOx排放量预测模型的基础上，利用IMVO算法对锅炉运行可调参数进行寻优，相比于MVO算法，改进多元宇宙算法具有更快的寻优速度和更好的寻优效果，可以更好地降低电厂燃煤锅炉的NOx排放浓度。