键合金丝可靠性强化试验失效机理仿真分析

王成，尹洪波，毛冰晨

（中国船舶重工集团公司第七二三研究所，江苏 扬州 225001）

0 引言

微波多芯片组件技术极大地促进了微波电子电路的发展，它是在高密度多层互联基板上利用微焊接技术和封装工艺组装微波电路的各个元器件，形成高密度、高可靠性、高性能和立体结构的电子装备的高新技术。金丝键合具有可靠性高、柔韧性好、密度高、工艺简单、价格低廉和应用范围广等优点，通常采用金丝键合工艺来实现单片微波集成电路，微波传输线、共面波导和集总式元器件之间的信息链接[1-3]。数据表明，90%以上的电子封装产品中使用了金丝键合技术。金丝键合作为微波多芯片组件中的关键工艺，其可靠性直接决定了组件的质量和可靠性[4-5]。键合金丝在使用环境中主要受热冲击和机械振动的影响，最终导致材料出现疲劳损伤失效[6]。

可靠性强化试验通过试验系统施加逐渐增大的环境应力和工作应力，以评估组件设计的可靠性，从而暴露出设计中的薄弱环节，便于前期的设计更改。某型号组件在10个周期的温度循环（-80～+125℃）及1 h的强化随机振动试验后电性能出现异常，振动频率为4 000 Hz，激励谱密度为1.5 g2/Hz，远大于GJB 360B组件的随机振动要求。开盖后发现部分键合金丝根部出现断裂。本文利用Ansys Workbench有限元软件对键合金丝在随机振动中的动力学性能进行分析，并基于Palmgren-Miner定律计算键合金丝的疲劳指数。分析的结果对后续的金丝键合设计及工艺优化具有一定的指导意义。

1 模型的建立

强化随机振动试验中根部断裂的键合金丝如图1所示，金丝采用楔形焊接，键合金丝的第一端点和第二端点所处的平面等高，金丝直径为25μm，通过显微镜测量得到其键合点间距D=3.5 mm，拱高H=0.7 mm。

图1 根部断裂的键合金丝

为了能够在Creo软件中准确地建立键合金丝的模型。首先，取根部断裂的键合点为直角坐标系的原点，建立键合金丝的曲线模型，如图2所示，采用二次曲线拟合的方法，得到键合金丝的函数方程z=0.228 5x2-0.8x。将得到的方程导入Creo软件中建立金丝的曲线模型，再导入Ansys Workbench中进行模态分析和随机振动分析。模型沿轴向采取扫略划分网格。端面采取四边形网格划分，沿轴向70等分。在键合金丝的两端施加全自由度约束以模拟金丝键合点的作用。键合金丝的材料物理性能如表1所示。

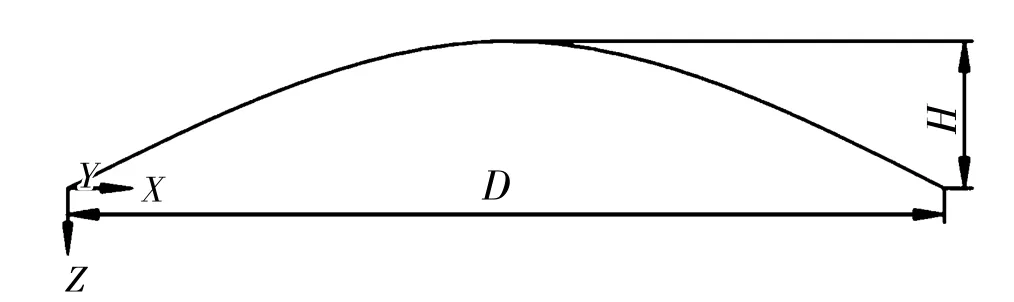
图2 键合金丝的曲线模型

表1 键合金丝的材料物理性能

2 随机振动仿真分析

2.1 模态分析

模态分析用于求模型的固有频率、振型和模态阻尼比等，是后续随机振动分析的基础。模态分析的目的是为了确定键合金丝的固有频率和相应振型。模态求解的阶数直接关系着后续随机振动分析的精度，因此，必须保证模型在某个方向上的有效质量与总质量的比值大于0.85。针对该模型，求得其前10阶的固有频率，前3阶的计算结果如表2所示。由于键合金丝的尺寸小、质量轻，因此模态频率较大。

表2 模态分析结果

各阶振型反映了键合金丝相对于初始位置的相对变化趋势。键合金丝前3阶的振型如图3所示。其中，第一阶的振型为沿Y轴方向左右摆动。一阶振型的相对位移较大，对其应力和应变都有较大的影响。

图3 键合金丝的前3阶振型

2.2 随机振动受力分析

强化随机振动的试验条件为X、Y、Z每个方向60 min，激励谱如图4所示。振动频率为20～4 000 Hz，激励谱密度为1.5 g2/Hz。

图4 随机振动激励谱

为了研究不同方向的激励载荷对键合金丝的受力影响情况，仿真了键合金丝在X、Y、Z方向的随机振动受力情况，其等效应力如图5所示，等效应力由“3σ”规则确定。从图5中可以看出，3个振动方向的最大等效应力都位于键合金丝的根部区域，这也是振动过程中最容易发生断裂的地方。且Y轴振动方向的最大等效应力值远远地大于另外两个方向的等效应力。由模态分析的结果可知，键合金丝一阶振型的固有频率为2 272.8 Hz，在强化试验随机振动的频率范围内，键合金丝在Y轴方向表现出共振行为。

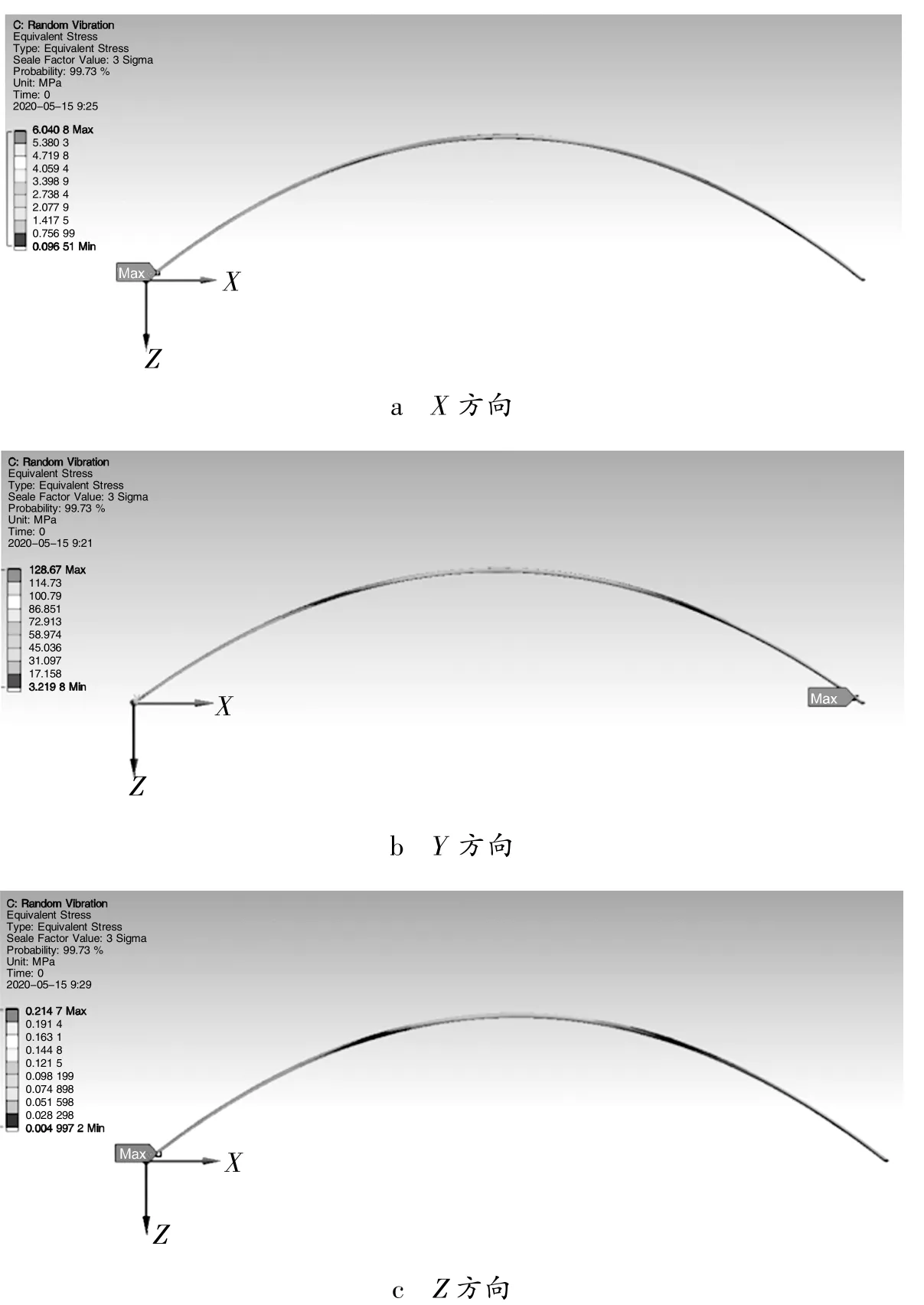
图5 X、Y、Z方向的随机振动等效应力

3 断裂结果分析

使用该组件装配时的劈刀键合100根金丝，选取10%进行拉力测试，测试时用微型钩子钩起金丝的中间，钩子以恒定的速度升起，直到金丝最薄弱的部位断裂，并记下此时所施加的拉力。键合金丝的拉力平均值为6.5 g，最低值为4.7 g，最高值为9.1 g。选取拉力平均值6.5 g，利用图2的金丝模型模拟拉力对金丝的作用，键合金丝在拉力值6.5 g时的等效应力如图6所示。

图6 键合金丝的等效应力

材料的疲劳数学模型如公式（1）所示：

式（1）中：S1、S2——应力水平；

N1、N2——应力水平对应的引力循环次数；

b——疲劳指数。

根据文献[7]，非铁金属的疲劳寿命为1 000次应力循环时，其所承受的应力水平为抗拉强度。b值取6.4。将图6中的最大等效应力值代入疲劳数学模型中，得到键合金丝的疲劳模型：

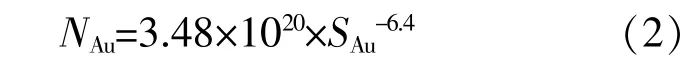
选取Y轴方向振动时最大等效应力的危险点S，X、Y、Z方向的随机振动在该点的等效应力结果如表3所示。

表3 应力分析结果

将表3中的X、Y、Z方向的等效应力值代入键合金丝的疲劳模型式中，计算得到X、Y、Z振动载荷下的金丝寿命，如表4所示。

表4 X、Y、Z振动方向下金丝的寿命

Palmgren-Miner定律是使用最广泛的线性累计损伤理论，材料各个应力下的疲劳损伤不受载荷顺序的影响，而是独立地继续进行的，总损伤可以线性累加。可通过以下公式计算金丝的疲劳损伤指数。

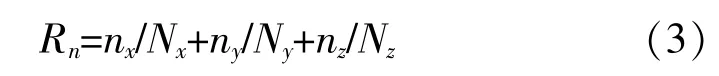
计算得到Rn=0.77。从计算结果中可以看出，X和Z方向振动激励的疲劳损伤指数远小于Y方向，相对于Y方向的疲劳损伤指数基本可忽略，因此键合金丝的疲劳损伤主要受Y方向的振动激励影响。另外，Rn值虽然小于1，但已大于电子设备测试中规定的0.7，存在较大的疲劳损伤的风险。

该组件在可靠性强化随机振动试验之前已进行了10个周期的温度循环（-80～+125℃）试验，由于键合金丝与基板之间的膨胀系数失配，交变的热应力易造成键合金丝的根部变形产生应力集中，使键合金丝产生一定的热疲劳。另外，计算上述的键合金丝的抗拉强度等效应力时键合金丝的拉力取值为6.5 g，而拉力测试时最小值为4.7 g，该值对应的键合金丝疲劳损伤指数Rn＞1。因此在1 h的强化试验随机振动条件下，Y方向振动载荷即对键合金丝造成了疲劳损伤，导致部分金丝发生了断裂。

4 结束语

文中利用仿真软件模拟了随机振动试验中不同方向的键合金丝等效应力，并根据Palmgren-Miner定律计算了键合金丝的疲劳损伤指数，计算结果表明键合金丝的断裂主要是疲劳损伤造成。该结果对于优化键合金丝的设计及工艺具有一定的指导意义，可通过以下方法进行改进。

a）劈刀的使用寿命对键合的强度有较大的影响，随着使用次数的增加键合金丝的拉力逐渐地减小。在20 000次的使用范围内，键合金丝的强度从最初的抗拉强度140 mN降低到35 mN，虽然能够满足GJB 548—2000中对规定的30 mN使用要求，但为了提高键合金丝的抗拉强度，应适当地减少劈刀使用次数。

b）优化键合金丝的工艺参数，如超声功率、键合的压力和键合面的温度等，以提高键合金丝的抗拉强度。

c）因为频率范围越接近组件的一阶固有频率，组件对激励的响应就会越大。设计的键合焊盘距离应尽可能地短，以减小键合金丝的跨度，并降低键合金丝的拱度，从而提高键合金丝的第一阶固有频率，增大键合丝的抗振能力，避免在随机振动频率范围内产生共振。