光谱数据解析中的变量筛选方法
2021-11-11李艳坤董汝南黄克楠毛志毅
李艳坤,董汝南,张 进,黄克楠,毛志毅
1.华北电力大学(保定)环境科学与工程系,河北省燃煤电站烟气多污染物协同控制重点实验室,河北 保定 071003 2.贵州医科大学食品科学学院,贵州 贵阳 550025 3.中国人民解放军陆军第八十二集团军医院,河北 保定 071000 4.天津市建筑材料科学研究院有限公司,天津 300110
引 言
随着测量技术的飞速发展,现代分析仪器的多个分析通道可提供丰富的数据,从而获取海量及高维数据变得愈加容易。然而在数据的多元模型构建中,不是所有的变量都适合进入最终的模型。冗余及干扰变量的存在都会影响模型准确性;或者有时获取某些变量的成本过高,从而需要摒弃某些变量;当然对因变量影响显著的自变量若未进入模型,也会影响模型的准确性。而通过筛选变量能够提取出代表体系组成和特点的信息变量,从而达到数据降维、模型简化、提高预测效率乃至提高模型解释或预测性能的目的。所以,变量筛选已成为目前多元模型构建中的一个重要步骤。近年来,光谱领域中变量筛选方法的研究取得了很大的进展。图1显示出变量(波长)筛选相关出版论文数量从2004年—2019年呈逐年增长趋势(来源:SCI-EXPANDED with searchtopic “variable-selection” or “wavelength-selection”)。光谱数据大都存在量大、波段数多等特点。例如,使用傅里叶变换近红外(near-infrared,NIR)分析仪时,6 000 cm-1光谱范围内可获得1 557个光谱点(变量)[1]。包括噪声、基线漂移、谱带重叠、背景干扰、杂散光等诸多因素的影响,会不可避免地导致数据中包含冗余和干扰变量。变量间存在的多重共线性也会影响建模,使得数据分析的结果变得不可靠。因此,变量筛选已经广泛地应用在光谱分析中。尤其近红外光谱(NIRs)吸收强度较弱,信噪比低,灵敏度低,谱峰宽且数目多、严重重叠。因此,借助化学计量学包括变量筛选技术从其光谱中提取出表征成分、结构等特征信息,克服了分析技术的难点,才使得该技术得以迅猛发展和应用。所以,目前变量筛选方面的综述[1-4]大都聚焦于其最得意的应用—近红外光谱领域。而本文结合作者的研究体会与文献调研,全面地综述了近/中红外光谱、拉曼光谱等光谱分析中常用的变量筛选算法的提出、发展、特点、分类及近年来的应用。
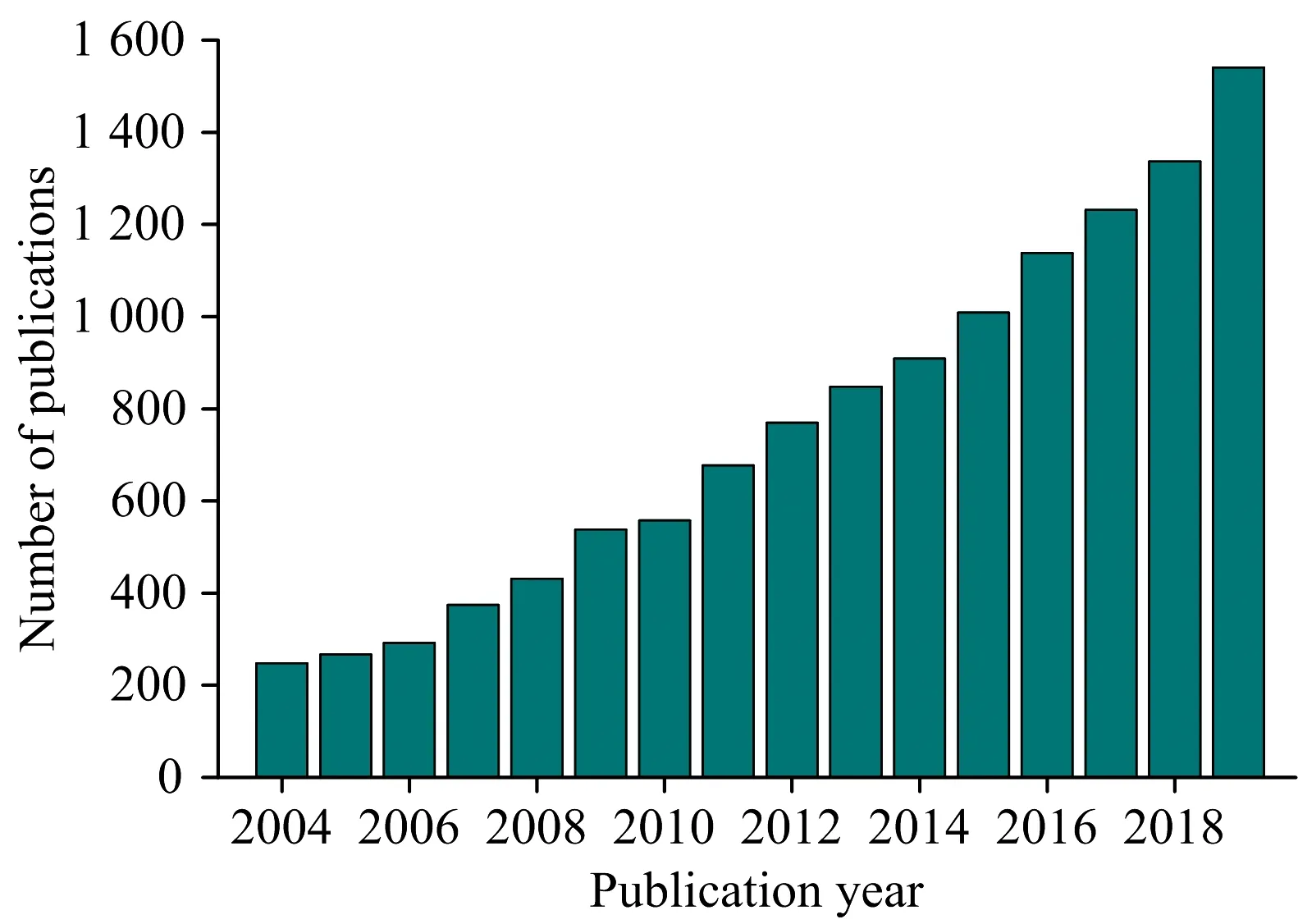
图1 变量/波长筛选相关论文出版数量
1 基于PLS模型参数的变量筛选方法及其应用
偏最小二乘(partial least squares,PLS)是由Wold等于20世纪末提出的一种经典的多元校正算法[5]。在最初始的非线性迭代偏最小二乘基础上发展了PLS-SVD算法、简化的偏最小二乘(SIMPLS)、非线性的Kernel PLS等。PLS求得模型的预报残差平方和较小,且适用于变量多、样本少的问题,得到广泛应用。同时基于PLS模型参数(回归系数、变量稳定性、变量投影重要性、光谱载荷权重)用于筛选变量的算法也在不断地应用在数据分析中。表1总结了代表性算法的提出及特点,并对其原理、发展及近五年来的应用进行综述。
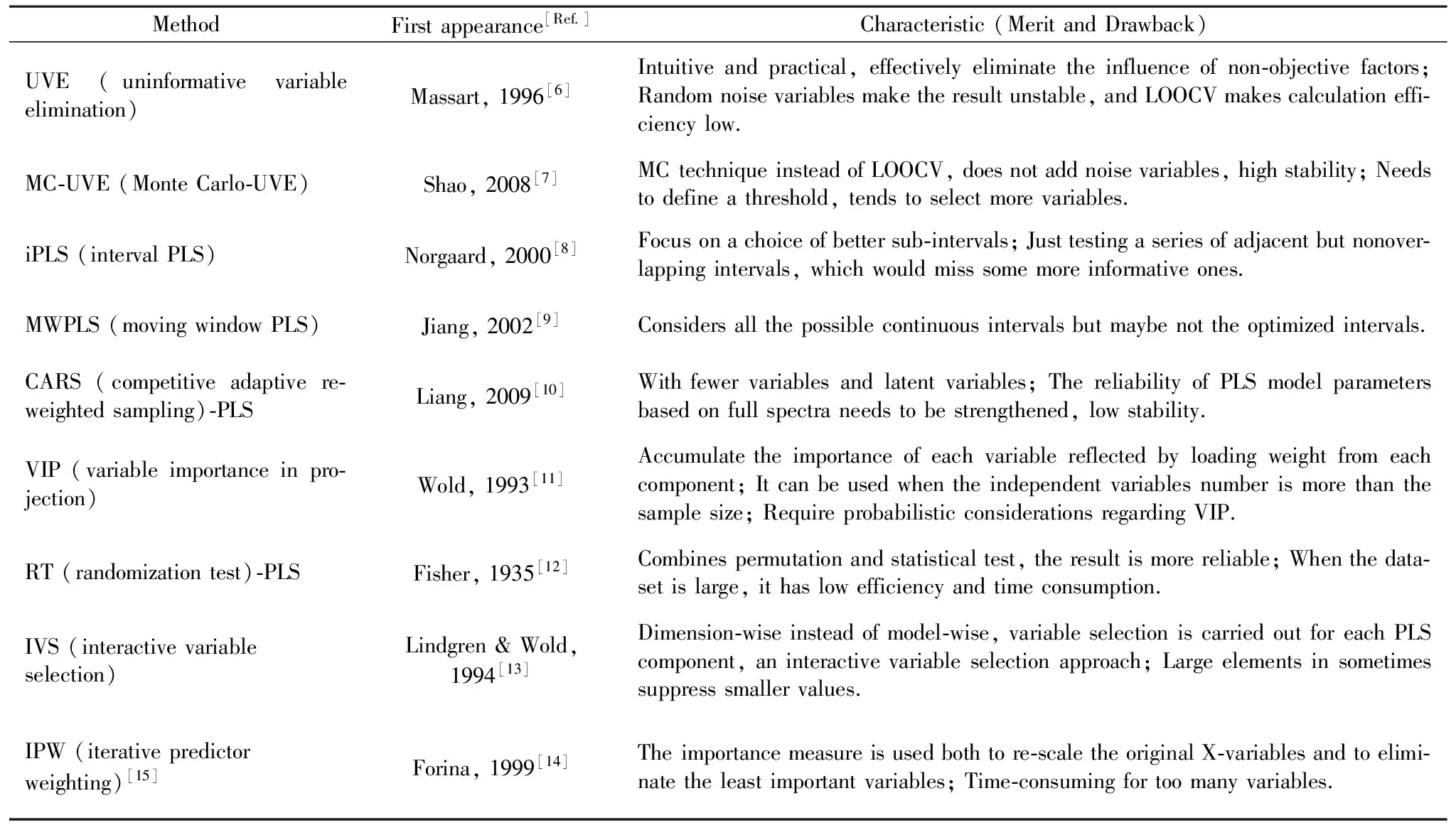
表1 基于PLS模型参数的变量筛选方法
1.1 无信息变量消除(UVE)-PLS
UVE通过留一交叉验证建立一系列PLS模型,计算每个变量的稳定性“stability”(回归系数平均值与其标准偏差的比值:“cj”)。通过在数据中添加数值较小的随机变量(噪声)的“cartif”作为阈值来删除无信息变量。邵学广课题组基于UVE融合蒙特卡洛(Monte Carlo,MC)思想,用MC技术代替LOOCV,提出蒙特卡洛无信息变量消除(MC-UVE)[7]。该方法对烟草样品的NIRs波长进行筛选,与全谱PLS及UVE-PLS相比,在保留变量数目最少的情况下取得最好的预测精度。并进一步和小波变换(WT)结合,得到更加精简的定量模型。此后,MC-UVE开始成功地应用于各种光谱数据的分析中[16-18]。
1.2 区间偏最小二乘(iPLS)和移动窗口偏最小二乘(MWPLS)
区间(间隔)PLS将光谱均分成若干个连续等宽子区间,在每个子区间内分别建立PLS模型,将交叉验证均方根误差(root mean square error of cross validation, RMSECV)最小的子区间确定为最佳模型波段。由于子区间的位置随着全谱划分区间数目的确定而固定,然而这些区间不一定恰与成分相关的信息区间吻合。为此,产生了采用一个窗口沿整个波谱逐步移动的策略,即MWPLS。
牛晓颖等[19]利用iPLS筛选出了猪、牛、羊肉等鲜肉中多种不饱和脂肪酸适宜建模的近红外光谱波段。Zhao等[20]运用iPLS分析猪肉皮下脂肪的拉曼光谱,实现了其含碘值的检测。Yu等[21]采用激光诱导击穿光谱技术结合iPLS,实现了含石油土壤中金属的定量分析。为了优化子区间的组合,出现一些iPLS改进方法:向前/向后区间偏最小二乘(BiPLS/FiPLS)、区间协同iPLS(SiPLS)和确定独立性筛选iPLS(SIS-iPLS)等[22-23]。许良等[24]采用近红外漫反射光谱结合MWPLS筛选克霉唑的特征波长区域,得到测定克霉唑粉末药品的最佳模型。谢军等[25]将MWPLS用于人血清葡萄糖的衰减全反射红外光谱分析中。Wang等[26]发展了深度协同-自适应移动窗口偏最小二乘-遗传算法用于煤样NIRs分析,得到水分、灰分、挥发物的最佳校准模型。还出现了窗口尺寸可变的CSMWPLS(changeable size MWPLS)、移动窗口组合搜索的SCMWPLS(searching combination MWPLS)、对称收缩循环固定窗口PLS(SCRUWPLS)[27]等。
1.3 竞争性自适应重加权采样(CARS)-PLS
CARS通过蒙特卡洛采样,利用指数衰减函数(EDP)和自适应重加权采样(ARS)策略选出PLS回归系数绝对值大的波长点,去除权重小的波长点,最终选出RMSECV最低值对应的变量子集。蒋雪松等用CARS-PLS建立了植物油反式脂肪酸的拉曼光谱定量模型,筛选出特征变量。Nie[28]等用CARS分析愈风宁心滴丸原料中葛根素,提高了检测精度。石岩等[29]用CARS研究人工牛黄的NIRs,用于建模的变量数大幅减少。Hu等[30]测定了葡萄酒中总酸、总糖和酒精含量,结果明显优于全谱PLS。融合MC-UVE和CARS优势产生了基于变量稳定性的SCARS(stability CARS),用于咖啡因、尼古丁、玉米中水分的检测[31-32]。Zheng等[33]提出双竞争自适应重加权采样(double CARS)。
1.4 变量投影重要性(VIP)分析
VIP分析中变量通过主成分传递对目标值的解释能力。若主成分对目标值的解释作用很强,而变量对主成分的作用又很大,则该变量会具有较大的VIP值,即被认为是贡献大的变量而被保留。Ferreira等[34]用VIP对巴西大豆的NIRs进行筛选,剔除了冗余变量,对大豆膳食纤维进行了准确分析。Gosselin等[35]提出PLS-bootstrap-VIP用于可见光-NIRs分析聚合物薄膜、木材/塑料复合材料、柴油参数,验证了筛选特征波长的有效性。
1.5 随机检验(RT)-PLS
邵学广课题组将随机检验(RT)思想引入PLS模型用于变量筛选。将数据对应的自变量值打乱,将随机化的自变量值与光谱响应值之间建立多个PLS模型。统计随机模型的回归系数值超过正常(真实)模型回归系数的比例(P),具有较小P值的变量即为重要变量。RT-PLS用于谷物和烟草NIRs波长筛选中,RMSEP平均值及标准偏差都小于全谱PLS[36]。同样构建了烤烟中三种多酚的近红外漫反射光谱模型,与采用高效液相色谱法测得的参考值一致[37]。
2 其他变量筛选方法
其他常见的光谱变量筛选算法按搜索及筛选变量的策略可以分为五类:(1)智能寻优算法:利用进化和群集智能算法,搜寻使目标函数较优的变量子集。其中遗传算法(GA)应用较广泛,在其基础上引入生物免疫系统原理,发展了免疫遗传算法(IGA)。结合GA、SA(模拟退火)算法优势,提出GSA算法[38];(2)基于模型集群分析算法[39]:采用随机采样(Monte Carlo,Bootstrap,Binary matrix)产生的变量子集建立系列子模型,挑选出RMSECV较低的子模型,采用统计检验评价变量的重要性,在下次迭代中赋予较高的取样权重。梁逸曾课题组基于模型集群策略提出一系列的算法;(3)基于变量空间共线性最小化算法:降低被选中变量建模的严重多重共线性,保留最小冗余信息的变量子集。例如,序列前进筛选法中的连续投影算法通过构建变量的正交矩阵来选择变量,降低了多重共线性变量对模型的影响;(4)基于分类模型的变量筛选:利用分类模型的内部参数作为评价,筛选出对分类模型有重要意义变量的同时,计算得到目标样本的得分用于分类判别。其中LDA[40]是降维和提取特征信息的有效方法之一。不相关变量投影分析(ULDA)考虑了基于LDA的变换矩阵列向量间的不相关性,减少降维后的数据冗余,在寻找疾病生物标志物中得到好的应用[41]。李艳坤等[42]用ULDA解析人体血清多肽质谱,从15 154个变量中挑选出7个特征变量较好地区分了良性和恶性肿瘤。不仅简化模型提高了诊断效率,而且7个特征变量所对应的多肽可作为潜在卵巢癌标志物;(5)正则化回归算法:在原有的损失函数的基础上增加惩罚回归系数的正则项,收缩回归系数,减少所有特征变量回归系数估计值的数量级,自动将无关变量的回归系数置接近于0。这几类算法包含的代表性算法总结于表2。
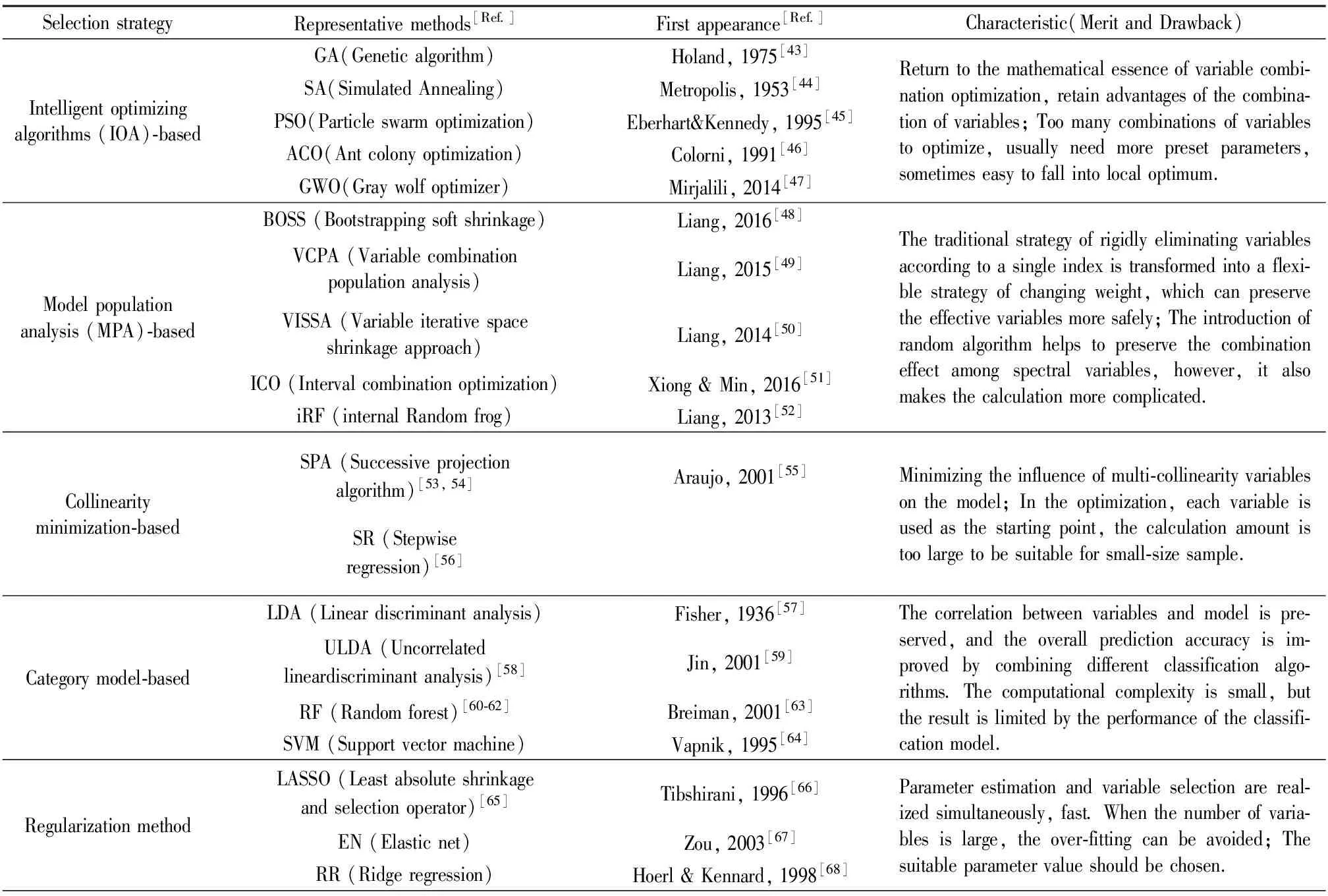
表2 其他光谱变量筛选方法
此外,还出现了基于其他原理的算法。通过将光谱投影到局部线性嵌入(locally Linear Embedding)[69]空间后,依次移除变量后引起样本位置的变化而提出一种用于变量筛选的方法。还提出潜变量投影图(latent projective graph)[70]等算法。
3 变量筛选方法的类别与比较
3.1 波长筛选和波段筛选
根据筛选出光谱变量的分布特征,分为波长筛选和波段(波长区间)筛选。波长选择(wavelength selection,WS)以波长点为单位(即一个变量),因此所选择的变量是离散的。波段筛选(wavelength interval selection,WIS)通常考虑相邻变量的连续和协同作用(正协同和副协同),可能增加选择变量的复杂性。而对光谱分段处理本质上降低了变量选择的难度,以划分的波长区间(若干连续变量组成)为单位寻找最优区间(组合)。但波段的划分很关键,图2展示了划分波段的四种方式[1]。其中,张进等提出的启发式最优波段组合(heuristic optimal partner band combination)[71]通过SPA选择冗余信息最小的变量,以此为中心向两侧扩展一定宽度,然后采用排列组合策略选出具有协同效应的波段组合,提高了基于变量直接排列组合的选择方法的效率[72]。
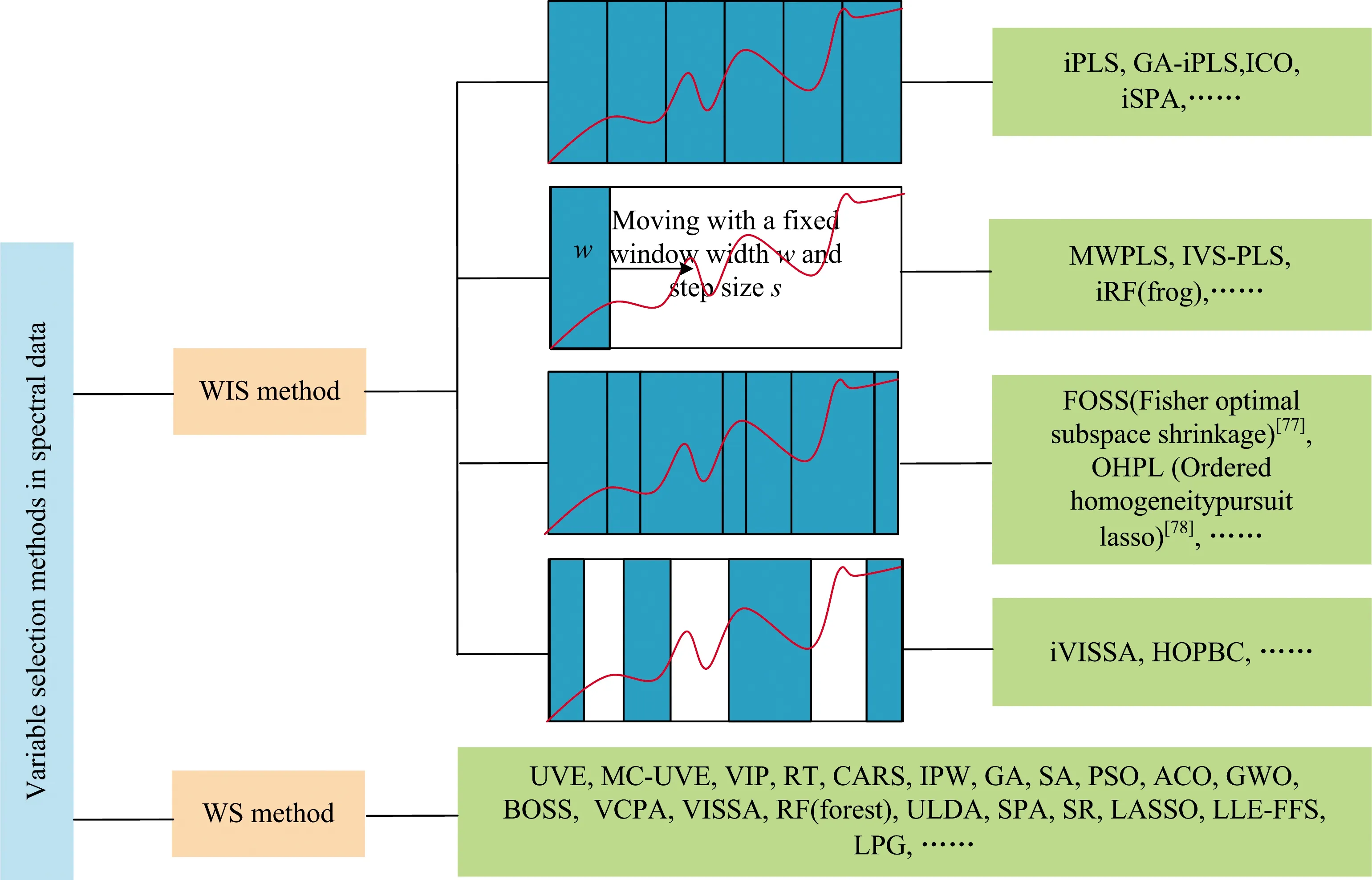
图2 波段和波长筛选方法
两类方法筛选出变量的分布虽具有相似性,但对模型预测能力的影响有一定的差别。一组谷物样本的近红外光谱(http://software.eigenvector.com/Data/Corn/corn.mat)和相应的蛋白质含量模型用于考察。首先利用小波变换结合多元散射校正对光谱进行预处理,然后采用UVE,iPLS和MWPLS等筛选出变量,如图3所示[73]。将筛选后的变量用于PLS建模,结果中MWPLS和iPLS的RMSEP值较低,也就是WIS的结果要优于WS。随后考察了光谱中变量间的相关系数,发现强相关变量分布比较连续。同时考察了一组强相关变量分布比较分散的烟草数据,筛选变量后用PLS建模预测尼古丁含量,发现WS比WIS方法的预测结果有优势。而两组数据无论使用波长筛选还是波段筛选,都优于全谱模型的预测结果。因此,筛选变量在光谱分析中非常有必要。而选择合适的波长或波段筛选方法,需在一定程度上考虑强相关变量的分布情况。
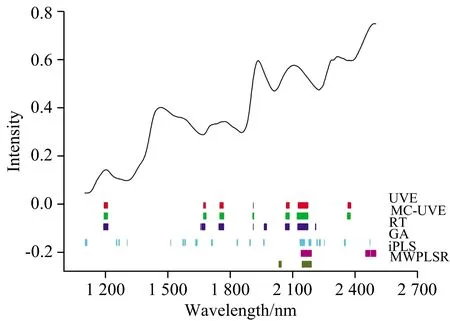
图3 谷物NIR-蛋白质模型变量筛选方法比较
3.2 过滤式、封装式、嵌入式方法
从变量子集选择标准与学习算法的关系角度,变量筛选方法又可以分为:独立于学习算法的过滤式、依赖于学习算法的封装式和与学习算法集成的嵌入式方法。过滤式(Filter)通过引入阈值来实现对变量的选择与否,方法与后续学习器无关。计算简便,但筛选结果受阈值影响较大;封装/缠绕式(Wrapper)使用迭代的过滤方法,将学习器的性能作为变量筛选的评价标准,直到选出最优变量组合;嵌入式(Embedded)利用模型的内部参数作为评价,保留变量和模型间的相互关系。变量选择方法自身即算法组成的一部分,嵌入到算法中。三类算法的流程及包含的常用算法如图4所示。
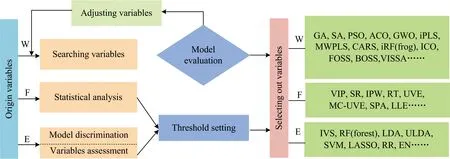
图4 过滤式、封装式和嵌入式方法
4 结 论
通过作者多年来在该领域的研究体会结合文献分析表明,每种变量筛选方法都具有各自的优势和局限性。实际中需要根据分析目标和算法本身两方面的特点选择合适的方法。下面围绕在解析实际体系中存在的若干问题进行讨论。
(1)有时单一的变量筛选方法往往达不到分析的要求,此时需要方法的联合使用,例如CARS-SPA和CARS-GA等等。联合方法不等同于几种方法的简单耦合,而是协同发挥优势。通常前一种粗选以消除无信息变量,后一种精选以挑选典型特征信息变量或降低变量间的多重共线性。最终选择的效果取决于不同算法的逻辑结合方式和综合利用度。
(2)某些筛选方法中由于采取随机抽样的变量子集和迭代方式进行优化,会导致模型筛选出的变量不稳定,进而产生不稳定的结果,降低模型的可信度。例如CARS尽管具有筛选出变量数目少的优点,但每次重复运行选中的变量个数及位置都会发生变化。对此,李艳坤等采取多模型共识策略[16, 18]综合多个成员模型的预测结果,或保留被选择频率较高的变量,得到更准确、稳健的结果。尤其应用在近红外光谱中,虽然其对应于结构信息的特征较差,但选定的波长与目标物的功能基团之间仍然得到了合理的解释。
(3)在寻找重要变量过程中,存在过拟合风险。由于数据包含大量的变量,总会有一些不相关变量由于偶然性而变得很重要[76],某些奇异样本的加入也会影响模型的构建。此外,采用RMSECV作为评价指标,或基于PLS回归系数的筛选方法[75]较多地利用自变量信息,这些都可能带来模型过拟合的风险。所以,尽可能地在建模前对数据进行奇异值的识别和剔除、采用独立的外部样本评估变量或大规模的数据集验证。而新的评价变量重要性的参数及其判据,以及搜索变量的策略和途径等工作仍需展开深入地研究。
(4)与尺度缩放、基线校正等光谱预处理方法(平滑、导数等)联合。李艳坤等曾利用小波变换系数替代原始光谱输入MC-UVE模型中,在保留更少变量时取得相当或优于原MC-UVE筛选模型的预测结果[7, 16]。此外,方法和数据属性之间可能存在相互作用,因此“不存在总是最好的方法,而存在最合适的方法”。所以,面对如此多的方法及方法的组合,可以发展集成(汇集预处理和变量筛选方法)智能化选择(根据数据特征或建模性能优劣,后者更简单直接)算法,并开发适用于测量仪器或独立使用的计算软件,使用起来会更加快捷,尤其对于非专业人士处理数据将会非常有用。
致谢:感谢邵学广教授(南开大学)对本稿件提供的宝贵建议与指导。
