基于时频矩阵局部对比度的跳频信号参数估计

刘佳敏，赵知劲,2，尚俊娜，叶学义

（1．杭州电子科技大学通信工程学院，浙江 杭州 310018； 2. 中国电子科技集团第36研究所通信系统信息控制技术国家重点实验室，浙江 嘉兴 314001）

1 引言

跳频通信具有低截获率、较强的抗多径、抗干扰能力以及组网能力等特点，也给跳频信号侦察技术增加了难度[1-3]。跳频信号参数估计作为侦察任务中的关键环节，受到国内外相关研究者的重点关注[4-6]。

跳频信号参数包括跳变频率、跳频周期和起跳时间等，主要有基于原子分解[7]、基于压缩感知[8]、基于时频分析[9]以及基于图像处理[10]等估计方法。其中，基于时频分析与基于图像处理的方法凭借其简单高效以及对非平稳信号分析的独特优势，成为目前的主流方法。文献[11-14]在不同时频分析技术的基础上提取跳频信号的时频脊线实现参数估计。文献[11-12]采用线性时频分布分析跳频信号，但不能兼顾时域与频域分辨率；文献[13-14]采用二次型时频分布，具有较高时频分辨率，但存在交叉项干扰。文献[15]将短时傅里叶变换（short-time Fourier transform，STFT）和平滑伪魏格纳分布（smoothed pseudo Wigner-Ville distribution，SPWVD）组合的时频分析方法，具有较高估计精度，但计算量大。文献[16]采用尺度不同的两个窗口对跳频信号进行双窗谱分析，在保证时频分辨率的同时降低计算复杂度，但估计性能受窗长的影响大。为了提高跳频信号参数估计性能，文献[17-20]将图像处理技术应用于信号时频图，以消除噪声和其他干扰信号的影响。文献[17]采用灰度共生矩阵提取时频图的纹理特征进行参数估计。文献[18-19]通过形态学滤波消除噪声和其他干扰信号，文献[19]在形态学滤波的基础上采用OPTA 细化算法对时频图像进行优化，但算法估计性能仍依赖于形态学结构元素的构造。文献[20]采用自适应形态学估计跳频信号参数，解决了形态学结构元素选择的普适性问题，但算法实现过程较为复杂。

传统局部对比度（local contrast measure，LCM）是一种根据人眼的视觉特性度量目标显著性的目标检测方法[21-22]。为提高低信噪比下跳频信号参数估计的精确度和算法性能的稳定性，本文提出了一种基于时频矩阵局部对比度（time-frequency matrix LCM，TFMLCM）的跳频信号参数估计算法。首先，利用不同尺度窗口计算时频矩阵上各点的局部对比度，实现跳频信号与背景噪声的分离；然后，根据时频矩阵上跳频信号的时频信息，完成对跳频信号的跳变时刻、跳变周期以及跳变频率的估计；最后，在DSP+FPGA的硬件平台上实现了本文算法对实际跳频信号参数估计的性能测试，验证了算法的实用性。

2 信号模型与时频变换

跳频信号是一种频率在伪随机序列的控制下不断跳变的非平稳信号，其数学模型为：

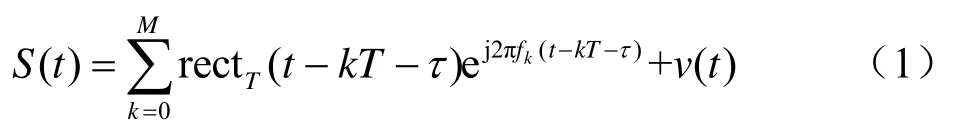
其中，T表示跳频周期， rectT(t)表示宽度为T的矩形窗，τ表示起跳时间，kf表示跳变频率，M表示观测时间内跳变频率总数，v(t)表示高斯白噪声。

对非平稳信号加窗处理得到多个短时平稳信号，并对这些短时平稳信号做傅里叶变换，进而得到跳频信号的STFT频谱。信号离散化后的离散STFT表达式为：

其中，h(n)表示窗函数，k=1,2,3, … ,K表示离散频率点，n=1,2,3, … ,N表示离散时间点。时频谱图定义为STFT模值的平方，具有较好的时频聚集性，其表达式为：

3 基于时频矩阵局部对比度的跳频信号参数估计

3.1 基于多尺度LCM的跳频信号提取

LCM通过计算图像各个像素点相对其邻域的对比特征，在提高目标对比度的同时抑制背景噪声，最后经过自适应阈值分离目标与背景。本文将跳频信号和噪声的时频谱图看作一个时频矩阵，利用跳频信号能量分布的特点，采用多尺度LCM获得跳频信号的局部特征区域块，实现跳频信号与背景干扰的分离。

3.1.1 传统LCM

传统的LCM采用固定尺度的滑动窗口逐一计算时频矩阵上各个点的局部能量对比特征值。如图1所示，滑动窗内区域由9个子块组成，当滑动窗口滑到时频矩阵上的某一处时，假设目标处于窗内中心块，则周围标号为1～8的子块wi(l,r)(i=1,2,3,… , 8)为其邻域背景块，每个子块中包含LR× 个时频点，第i个子块的能量均值为：

图1 滑动窗口遍历时频矩阵

则各邻域子块中能量均值的最大值为：

其中，n表示表滑动窗的第n次滑动，再找到中心块0(,)wlr的时频能量最大值nL：

为增强目标所在区域的对比度，定义局部能量对比特征值为：

将此对比特征值nC替换处于滑动窗口第n次滑动所在区域中心时频点的能量值。根据式（4）～式（7）使用滑窗对时频矩阵从上至下，从左往右依次遍历，得到经LCM处理后的特征矩阵。

一般选取尺度为9× 9共81个像素点作为每个子块的最大的尺寸[13]。当选取尺度为L=R=6和L=R=9的滑窗对图2（a）中的时频图进行LCM处理，结果分别如图2（b）和图2（c）所示。当接收信号中存在能量较高、持续时间较短的突发信号时，由于选取的模板不恰当，图2（b）中无法有效抑制突发信号干扰，将产生虚警概率，图2（c）中能抑制大部分干扰。由此可知，窗口大小的选取将影响检测效果，故提出一种多尺度LCM应用于跳频信号提取。

图2 不同尺度模板下的LCM处理结果

3.1.2 TFMLCM

考虑到跳频信号驻留时长的未知性以及跳频信号的时频信息分布特点，研究了一种多尺度窗口的LCM应用于时频矩阵，分离跳频信号。

首先，将时频谱图上各点值按式（8）归一化到[0,255]，得到时频矩阵 (,)knI：

其中，max_I和min_I分别表示原时频谱图上的最大值与最小值。

对于大小为KN× 的时频矩阵 (,)knI，时频矩阵的各行代表频率分辨率为的频率分布。

其中，fs为信号的采样频率。窗口尺度的选取取 决于时频矩阵的实际大小。为提高跳频频率估计精度，令各尺度窗口的子块的行数为3，按照图1（b）中滑窗与子块大小的关系，将窗口的行数固定为9。由于跳频周期的不可预知性，选取多个列数不同的窗口分别对原时频矩阵进行滑窗处理，若最小窗口的列数为 1N，则其他窗口列数取 1N的整数倍，且始终令滑窗列数的取值范围在[6, 0.3×N]之间。同时，为保持多尺度局部能量对比特征值计算前后时频矩阵的尺度不变性，对时频矩阵I(k,n)按照不同窗口尺度向四周进行扩充，得到预处理后的时频矩阵qi(k,n)。对于窗口尺度为9 ×N1的模板，I(k,n)扩充后的情况如图3所示。根据原含噪时频矩阵I(k,n)的实际取值，矩阵扩充部分的取值为[0,10]区间的随机数，对应高斯噪声。

图3 扩充后时频矩阵 1(,)knq

对不同尺度窗口下预处理后的时频矩阵qi(k,n)上的各点按式（4）～式（7）分别计算局部能量对比特征值，并提取原时频矩阵所对应区域，得到特征矩阵qi′(k,n)，i取1,2,…,Z，Z为滑动窗的个数。按式（9）计算不同滑窗尺度下的特征矩阵的均值，以减少因滑窗尺度选取不当造成的虚警或漏检现象，最终得到多尺度时频局部能量对比特征矩阵Q。

其 中，i取 1,2,…,Z；k=1,2,3,…,K；n=1,2,3, …,N。

选取合适的门限阈值 Th ，当矩阵Q上某点的值大于该门限时，即存在跳频信号，利用式（10）分离出跳频信号时频矩阵P。

其中，u和σ分别表示矩阵Q的均值和标准方差，β表示自适应分割系数，根据实验经验通常取3～8；k=1,2,3,… ,K；n=1,2,3,…,N。

3.2 跳频信号参数估计

经TFMLCM处理后得到的矩阵P仅保留了跳频信号的时频信息，在矩阵P上依次搜寻每一列的峰值点，即若P(imax,j)=max(P(:,j))，则F(j)=imax，其中，imax的取值范围为1,2,3,…,K，j=1,2,3,...,N。

数组F表示各个时间点的信号频率分量，对F各前后两个元素求差分，找到跳频信号频率发生跳变的时刻点所对应的列，存入集合Stp，如式（11）所示。

其中，u1表示差分阈值，取值为子块的行数3。假设满足式（11）的跳变时刻点的个数为Nt，则i=2,3,4,…,Nt+1；j=1,2,3,…,N；且令 Stp (1)=0， Stp (Nt+ 2)=F(N)。则跳频信号的跳频周期和起跳时间估计值分别为：

其中，wT表示观测时长，N表示时频矩阵列数。取相邻跳变时刻之间的所有时间点上跳频信号频率值的均值为该跳的信号频率估计，即：

其中，Fmean[a,b]表示取数组F第a个元素至第b个元素之间所有取值的平均值，i=1,2,3,…,Nt+1，fs表示采样频率，K表示时频矩阵的行数。

3.3 算法流程

本文所提出的基于时频矩阵局部对比度的跳频信号参数估计算法的步骤如下。

步骤1利用式（2）和式（3）计算接收信号的时频谱图，得到SPECs(k,n)。

步骤2按照式（4）～式（10），利用TFMLCM对预处理后的矩阵进行遍历，并将跳频信号与背景噪声分离，得到时频矩阵P。

步骤3在纯净的跳频信号时频矩阵P上按列搜寻，通过数组F记录每个时刻点的频率分量。

步骤4利用式（11）找到频率剧变的时刻点Stp ()i，即每一跳的跳变时刻点所在列。

步骤5根据跳变时刻点集合Stp，通过式（12）～式（13）分别估计出跳频信号的跳频周期Et和起跳时间Est。

步骤6利用式（14）估计跳频信号的各个跳变频率。

4 算法仿真与测试

4.1 算法仿真与性能分析

为验证算法的有效性，定义当跳变时刻点的个数比实际跳频个数少1时，能正确提取出跳频信号。跳频信号提取正确率为：

其中，C表示实验总次数，C0表示正确提取出跳频信号的实验次数。

采用归一化均方误差来衡量跳频信号各个参数的估计性能，式（16）～式（18）分别表示起跳时间、跳频周期和跳变频率的估计误差。

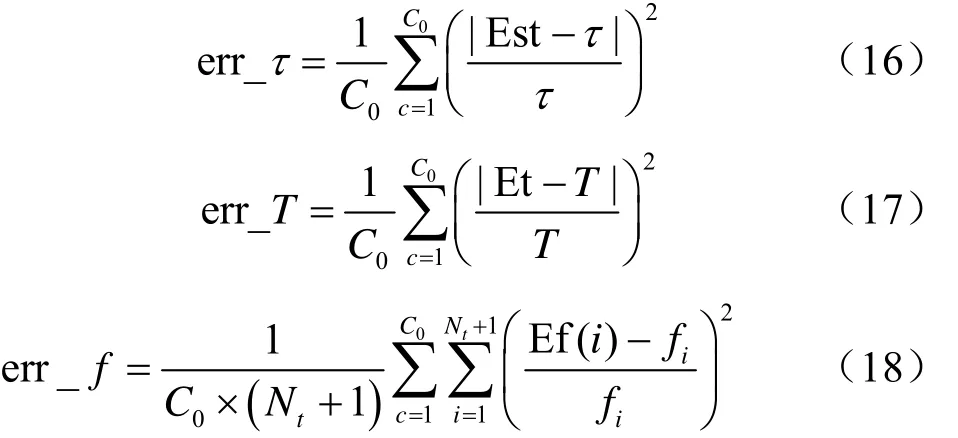
其中，τ、T、fi分别表示跳频信号的实际起跳时间、跳频周期和跳变频率。

假设信号的采样率为100 MHz，观测时长为0.4 ms，跳频信号的频率集为[13.5，9.9，16.2，9，10.8，5.4，19.8，12.6，14.4，7.2，27.9，22.5，11.7，28.8，30.6，26.1，18，15.3，29.7，23.4] MHz，跳频周期为0.02 ms，共20跳，同时存在功率与频率随机变化的突发信号。滑动窗口的尺度选择如下：①单尺度滑动窗尺度为96× ；②单尺度滑动窗尺度为99× ；③多尺度滑动窗尺度为[9 × 9,9× 18,9 × 27]以及④多尺度滑动窗尺度为[9×1 2,9 × 24,9 × 36]。以下所有实验结果均由100 次蒙特卡洛仿真结果求平均所得。

实验1跳频信号提取效果分析。选取滑动窗①～④，利用TFMLCM分别提取跳频信号，提取正确率与信噪比的关系与文献[9-10]通过形态学滤波实现跳频信号与背景干扰的分离，其信号提取正确率对比，如图4所示。由图4可见：在信噪比低于-8 dB时，TFMLCM的信号提取正确率高于80%，而LCM法低于30%，基于形态滤波算法失效，故本文的TFMLCM比两种对比算法在低信噪比下具有更好的提取效果；基于多尺度滑动窗③、④的提取正确率分别在-5 dB和-7 dB信噪比时达到100%，受窗尺度影响小；而基于单滑动窗①、②的信号提取正确率分别在-4 dB和0 dB信噪比时达到100%，且受窗尺度影响大；形态滤波法在信噪比接近3 dB时，信号提取准确率才达到收敛，本文基于③、④窗的TFMLCM分别提高信噪比达8 dB、10 dB。

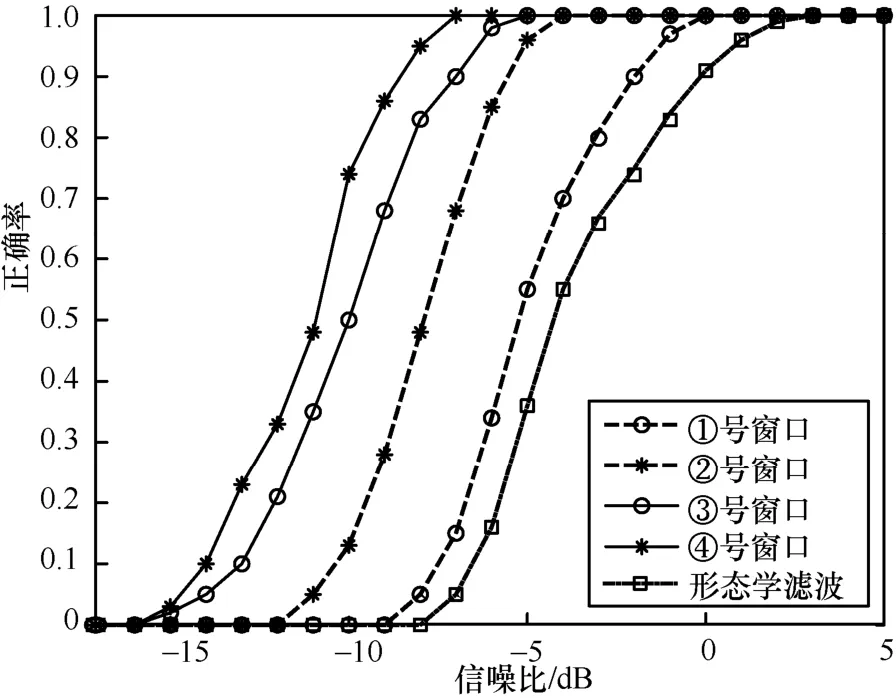
图4 不同滑窗下的信号提取结果

实验2本文所提TFMLCM（选④号窗口）、LCM（选②号窗口）以及形态学滤波算法对跳频频率、起跳时间和跳频周期的均方误差分别如图5～图7所示。由图可见，本文TFMLCM的跳频频率估计性能优于两种对比算法。在形态学滤波法进行信号提取的过程中，由于二分阈值以及滤波结构元素选取的影响，形态学滤波法的起跳时间估计性能比基于局部对比度的两种算法降低一个数量级。本文TFMLCM的跳频周期估计精确度达到 10-4，性能远胜于两种对比算法。

图5 跳频频率估计误差

图6 起跳时刻估计误差

图7 跳频周期估计误差

4.2 算法性能测试

基于DSP+FPGA芯片的平台搭建了跳频信号参数估计算法测试系统，在CCS7.2集成开发环境 编程实现参数估计算法并进行了调试，通过SEED-XDS200仿真器将工程文件下载至芯片内，进行实时测试，验证算法的正确性和实用性。

4.2.1 测试系统组成

基于TMS320C6678DSP和Kintex-7 XC7K410T FPGA芯片的硬件系统设计的跳频信号参数估计算法性能测试系统组成如图8所示。整个性能测试系统由信号源、射频前端、数据处理模块以及显示模块组成。数据处理模块作为参数估计算法测试系统的核心部分主要包括用于接收基带数据的FPGA、执行参数估计算法的 DSP 以及提供高速缓存区域的DDR3。首先，信号源采用SMBV100A信号发生器，发射跳频信号，在射频前端利用 AD9361将接收到的模拟信号下变频至零中频信号，并得到正交的I、Q两路信号，对两路信号分别进行采样并传输给数据处理模块；然后，FPGA将接收到的零中频数据通过SRIO传输到DSP外接的DDR3中，DSP在初始化SRIO后与DDR3进行数据交互；同时，为使数据得到高效处理，在DDR3中设计Ping-Pong结构的缓存共享内存，进行轮流读写，当零中频数据在Ping-Pong区域中的任一区域存满后会通过GPIO中断通知DSP，DSP将从另一内存区域读取数据进行后续的跳频信号参数估计，提高了数据吞吐量与系统通信速度。在DSP平台上编程实现上文的跳频信号参数估计算法；最后，DSP通过UART与上位机进行通信，将跳频信号参数估计结果显示在液晶屏幕的接收内容显示框。

图8 测试系统组成

4.2.2 算法实测结果及分析

将信号发生器SMBV100A的发射功率设为-10 dBm，射频中心频率为1 150 MHz；射频收发接收器AD9361的通带带宽为50 MHz，采样率设置为100 MHz。跳频信号的跳变频率集为[28.8, 30.6, 26.1，13.5, 9.9, 16.2, 20.7, 18.9, 24.3, 27, 9, 10.8, 5.4, 19.8, 12.6, 14.4, 7.2, 27.9, 22.5, 11.7, 18, 15.3, 29.7, 23.4, 4.5] MHz，跳变周期为0.02 ms。

单纯的载波信号和跳频信号在A/D转换后，经FPGA传至DSP，在CCS7.2上编程计算其1 024点的傅里叶变换，得到的功率谱分别如 图9（a）和图9（b）所示。可以看出信号在传输过程没有出现失真现象，验证了信号收发和功率谱计算功能的正确性。

图9 信号功率谱

将发射功率设置为-25～20 dBm，每间隔5 dBm进行100次参数估计。不同发射功率跳频周期和跳变频率的估计误差如图10所示。在低发射功率时，仍然能以较小估计误差估计出两种参数，估计误差均随发射功率的增大而减小，且跳变频率的估计误差能达到 10-5的数量级。由于发射端源源不断地传输信号，实际跳频信号的起跳时间无法预知，故无法统计跳变时刻的估计误差，但从式（12）和式（14）可知跳频周期与跳变频率的估计依赖于跳变时刻点的估计，图10所示的这两种参数的良好估计性能侧面证明了本文算法也能够准确地估计实际信号的各个跳变时刻点。

图10 不同发射功率下的参数估计误差

5 结束语

本文提出了一种基于时频矩阵局部对比度的跳频信号参数估计算法。该方法利用多尺度局部对比度算法计算时频图上各点的能量对比特征，降低了由某些能量较高的噪声点以及随机的突发 干扰导致的虚警概率，具有较强的鲁棒性。仿真结果表明，本文算法对跳频信号各参数的估计性能优于其他同类算法，实际信号参数估计的测试结果表明该算法具有实用性。在后续研究中可利用多核DSP芯片八核并行结构的特点，设计多核数据处理流程框架实现该算法，以进一步提高算法实时性。