单层二硫化钼的光致发光与能谷极化研究

万 逸,崔 冬,胡 婷

(南京理工大学 理学院,江苏 南京 210094)

除电荷、自旋之外,电子还具有能谷这一内禀自由度。能谷,表示的是固体材料能带结构的极值点。传统的微电子学,主要基于电荷自由度,已发展出超大规模的集成电路;新兴的自旋电子学,以自旋自由度作为信息载体,在提高存储密度、加快运算速度等方面发挥积极作用。研究者们借鉴自旋电子学的研究思路,尝试以能谷自由度作为信息载体,调控“能谷比特”,设计并实现功能器件,这就是“谷电子学”的由来[1-4]。利用材料本身的磁、电、光、力等性质,有助于实现运算、存储、通信等逻辑功能的高度集成[5];基于能谷自由度的新型功能器件,更是构筑量子计算和量子通讯的重要基础[1-4]。

在二维过渡金属硫族化合物(Transition metal dichalcogenides,TMDs)材料中,存在能谷与自旋的强锁定,这为自旋电子学和谷电子学提供了一个丰富的研究体系[6]。以二硫化钼(MoS2)为例,其单层材料具有的直接带间跃迁,使得能谷具有额外的轨道磁矩,角动量守恒又确保这一跃迁遵循光学选择定则[7-9];在圆偏振光的激发下,可以产生非平衡状态下极化的谷电流[10];理论预言的谷霍尔效应,已被实验所证实[11,12];样品层数与能谷自由度之间的耦合,有望应用在量子计算领域[5]。为了定量分析能谷极化,研究者们引入可测物理量,能谷极化率(Valley helicity),通常以P表示[7-9]。理想情况下,P=100%,这意味着特定旋度的圆偏振光只能激发特定能谷。但是,由于存在谷间散射和激子弛豫,实际测量的室温极化率仅能达到10%～30%,偏振度较低,这就意味着,在圆偏振光选择性激发能谷的过程中,两个能谷之间仍然存在耦合,这对于研究者所期望的,将两个能谷作为0和1两个逻辑单元非常不利。此外,即使是在完全相同的测试条件下,对于不同的单层样品,能谷极化率也会存在明显的差异,关于此现象一直缺乏明确解释和深入分析。

本文以633 nm激光进行共振激发,观测到在化学气相沉积(Chemical vapor deposition,CVD)方法合成的单层MoS2中,光致发光(Photoluminescence,PL)强度与能谷极化率之间存在逆向关联。对照可知,高质量的单层MoS2样品,呈现较强的光致发光强度,及较低的能谷极化率;低质量的单层MoS2样品,呈现较弱的光致发光强度,及较高的能谷极化率。通过分析MoS2直接带间跃迁遵循的光学选择定则,本文对于量子产率与能谷极化之间的关联进行了研究,以期发现能谷极化率的差异,主要在于不同的激子弛豫时间。这一研究工作可能为实现能谷的有效调控提供新思路。

1 单层二硫化钼的制备与表征

二硫化钼样品是通过CVD方法,以硫粉(99.999%)、MoO3粉末(99.99%)作为固态生长源,惰性气体Ar为载气,覆盖有285 nm SiO2层的Si基片作为沉积衬底,旋涂一种名为PTAS(50 μmol/L)的有机染料作为成核中心,合成出来的,如图1(a)所示。将硫粉与MoO3粉末在40 min内,分别加热至160 ℃和650 ℃,保持5～10 min,随后自然冷却至室温。

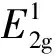
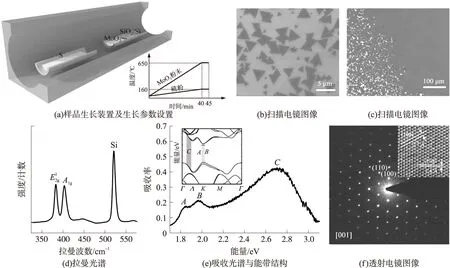
图1 单层MoS2的制备及表征

为检验样品结晶质量,单层MoS2样品被转移到铜微栅上。如图1(f)所示,高分辨透射电镜图像呈现出Mo原子的周期性排列,(100)和(110)晶面间距分别为2.7 Å和1.6 Å。选区电子衍射图案清晰,只观察到一套六重对称衍射斑点,说明MoS2样品在较大范围内结晶方向统一,可判断材料在选取范围内为单晶。

2 能谷关联的光学跃迁定则

牛谦等在研究电子半经典动力学行为时发现,布洛赫电子波包围绕其中心的旋转携带轨道磁矩,由此提出利用轨道磁矩和贝瑞曲率对能谷进行描述,贝瑞曲率被描述为参数空间的一个有效磁场[16]。类比于自旋的向上和向下,可以由符号相反的磁矩来描述[17];位于两个简并但不等价能谷处的电子,也可以认为是能谷赝自旋向上和向下,由此引入能谷因子(±1)的概念。

考虑一个处在非简并能带n上的电子运动,在原本的基础上还需要加上一个贝瑞曲率项

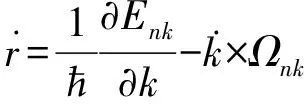
对于单层MoS2,其布里渊区不等价能谷K与K′的贝瑞曲率大小相同、符号相反。如果施加平面内电场,不等价能谷的载流子会发生空间分离,将会在垂直电场方向上产生横向电流,这就是“谷霍尔效应”。谷霍尔效应的存在,使得研究者们可以通过电场或磁场来产生和探测能谷的极化,运用能谷自由度来储存和处理信息[11,12]。

从轨道对称性出发,分析单层MoS2光致发光过程的圆偏振选择性[18]:对于MoS2,布里渊区边界的两组能谷K与K′,波矢群为可交换的阿贝尔群C3h,在三重旋转操作C3和镜面操作σh下保持不变。对称操作C3和σh将Mo原子d轨道分成3组,分别为A′(dz2),E′(dxy,dx2-y2),和E″(dxy,dyz)。第一性原理计算表明,价带顶和导带底分别由(dxy,dx2-y2)和(dz2)贡献,因此布洛赫波函数分别为

式中:c和v分别指代导带底和价带顶,±1为能谷因子。在三重旋转操作下,应满足

式中:ma为轨道磁量子数。

若等式成立,要求exp[i×2π(mf-mi∓1)/3]=1,即(mf-mi∓1)是3的整数倍。

对于单层MoS2,能谷K满足mf-mi=-2,因此只有左旋圆偏振光(σ+)激发,才可以实现K点处价带顶至导带底的跃迁;相应地,在K的时间反演点K′处,满足mf-mi=+2,此时只有右旋圆偏振光(σ-)激发,才可以实现K′点处的带间跃迁。

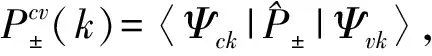
以描述左旋(σ+)与右旋圆偏振光(σ-)吸收的差异。单层MoS2的能带结构如图2所示,在具有时间反演对称性的两组能谷K与K′中,自旋轨道耦合作用下价带劈裂而形成的A、B激子,两者的跃迁,均遵循能谷关联的光学选择定则,跃迁能量ћωcv(k)=εc(k)-εv(k)。在K能谷中,A、B激子跃迁仅对左旋圆偏振光(σ+)响应;相应地,在K′能谷中,仅对右旋圆偏振光(σ-)响应,实验观测结果与理论预言较好地符合。香港大学的崔晓冬课题组与美国哥伦比亚大学的T. F. Heinz课题组均通过实验验证[8,9],可以利用光的圆偏振特性,实现对于能谷赝自旋的调控。

3 圆偏振光致发光光谱

圆偏振光致发光的测量光路如图3(a)所示,设计思路如下:线偏振的633 nm激光在经过1/4波片后转换成圆偏振光照射到样品上,假设样品上出射的信号光,由左旋圆偏振光(σ+)与右旋圆偏振光(σ-)共同构成。左旋、右旋圆偏振信号光经过1/4波片后,将转变为p偏振和s偏振线偏振光。此时,使用一个线偏振片作为检偏器,在光谱仪前分别阻挡p偏振和s偏振中的其中一束,仅让另一束通过,两次测量,即可得知两者强度,以两者之差除以两者之和,得到极化率P。测试结果如图3(b)所示,在单层MoS2的光致发光光谱中,若采用左旋圆偏振光(σ+)激发,则左旋圆偏振光(σ+)的强度始终要高于右旋圆偏振光(σ-),充分遵循光学跃迁选择定则。不过由于是在室温下进行测量,单层MoS2的极化率并没有很高,仅为17.6%。另外,真空环境和大气环境下测得的光致发光谱无明显差异,因此可以排除物理吸附的影响。

图3 单层MoS2的圆偏振光致发光谱

如图4(a)所示,这是利用CVD方法,在SiO2/Si衬底上合成的单层MoS2。由于硫源的供给不足,样品中将有少量硫空位产生,样品呈现为“内凹”三角的形状,与“理想晶格”的等边三角形存在差异。此样品的光致发光没有等边三角形MoS2均匀,但更利于说明MoS2光致发光与能谷极化的关系。以633 nm的左旋(σ+)圆偏振光激发样品,逐点扫描,先后测量左旋(σ+)和右旋(σ-)圆偏振出射光强度Iσ+和Iσ-。图4(c)为A激子光致发光强度(Iσ-+Iσ+)分布,图4(d)为能谷极化率P=(Iσ+-Iσ-)/(Iσ++Iσ-)分布。可以看出,对于此样品,中心区域发光最强,边缘较弱;但是,能谷极化率却是中心区域最低,边缘较高。可以看出,在光致发光强度与能谷极化率之间,存在着较为明显的逆向关联,如图4(b)所示。

图4 单层MoS2光致发光与能谷极化的比较

4 光致发光量子产率与能谷极化率的负向关联

对于特定的材料体系,辐射复合时间τr可视为常量。由QY≈1/(1+τr/τ)可知,在τr保持不变的前提下,较高的QY对应于较长的激子弛豫时间。

从微观上来看,能谷极化率与激发光在K与K′处产生的激子数量存在以下关联

式中:NK和NK′分别表示K与K′能谷处的激子数量。推导可知,能谷极化率与激子的产生、复合和弛豫,以及能谷赝自旋的弛豫,存在以下关系

式中:τ为激子弛豫时间,τv为能谷寿命,P0为一常数。

因此,在能谷寿命保持不变的情况下,能谷极化率随激子弛豫时间的延长而降低。换而言之,量子产率越高,光致发光强度越高,能谷极化率越小,这一结论与图4的实验结果保持一致:在光致发光强度最高的样品区域,测得了最低的能谷极化率。

5 结束语

本文探讨了以MoS2为代表的谷电子学材料中能谷内禀属性关联的物理性质的科学内涵,着重分析了能谷关联的光学跃迁选择定则;借助共振激发,利用圆偏振光激发化学气相沉积法合成的单层MoS2样品,对其光致发光谱中的左旋与右旋信号分别进行采集,发现在单层MoS2的光致发光强度与能谷极化率之间,存在一种逆向关联,这与“高质量样品,高极化率”的习惯性认知有所区别。从微观角度进行分析,得出结论:不同的激子弛豫时间是导致极化率差异的主要原因。这意味着,可以通过在谷电子学材料中进行晶格修饰或引入掺杂,调节体系的载流子动力学过程,以实现对于室温能谷极化率的有效调控,减弱简并能谷的耦合,为实现新型自旋器件和谷电子学器件提供新途径。