“高分二号”卫星双相机影像几何拼接方法

刘洋 李进喜 王春发 谭健

“高分二号”卫星双相机影像几何拼接方法

刘洋 李进喜 王春发 谭健

（甘肃省地质矿产勘查开发局第三地质矿产勘查院，兰州 730050）

“高分二号”卫星采用两台相机拼幅成像的方式来增大幅宽，为了提高数据的使用效率，要求提供统一几何精度的拼接产品。由于相机间重叠区域小，交会条件弱，传统拼接方法难以适用。针对此问题，文章提出一种数字高程模型（Digital Elevation Model，DEM）辅助区域网平差的物方几何拼接方法。该方法充分利用相机影像的定向参数，构建基于有理函数模型的物方帧间几何配准模型，以DEM作为高程约束，求解相机间影像几何配准参数，在物方实现影像高精度几何拼接。该方法应用于“高分二号”卫星上两台相机影像拼接结果表明，不同精度DEM辅助拼接的条件下，影像搭接区拼接精度均达到子像素水平，验证了该方法的有效性。

弱交会 几何拼接 数字高程模型 “高分二号”卫星 遥感应用

0 引言

“高分二号”（GF-2）卫星作为我国高分辨率对地观测重大专项卫星，可以为用户提供高精度的对地观测数据，能够满足用户多行业的应用需求[1]。为了满足用户对幅宽的需求，国产高分遥感卫星均采用多台相机拼幅成像的方式，每台相机为中心投影成像，GF-2卫星相机便采用此类设计。图1为GF-2卫星相机几何特性（为相机本体坐标系，原点为相机摄影中心，轴垂直于探测器线阵方向，以卫星飞行方向为正，轴沿着探测器线阵方向，轴沿着相机光轴方向，指向地面为正），相机间夹角为2.01°，重叠区为380像素，可见交汇条件非常弱[2-3]。为了提高GF-2卫星数据的使用效率，需要提供统一几何精度的高品质拼接影像产品。在摄影测量数据生产中，影像的拼接精度会直接影响后续摄影测量生产的精度，若拼接精度不高会导致数字高程模型（Digital Elevation Model，DEM）精度有损失。亚像素级的相机间影像拼接精度是保证DEM生产精度的前提。如何对多台相机成像的影像进行高精度的几何拼接，成为了高分辨率遥感卫星应用中亟待解决的问题。

图1 “高分二号”卫星双相机成像几何特性

目前，针对高分辨率卫星多相机和多片探测器影像几何拼接的应用需求，国内外学者开展了大量研究，并取得了较好的效果。总体而言，多相机多片探测器影像几何拼接方法可以分为两类：像方拼接方法和物方拼接方法[4-5]。文献[6]对印度IRS-1C卫星上的全色相机的3个交错排列CCD成像的多幅影像，采取简单的影像像面间平移的方式进行拼接。此方法具有模型简单，计算量小的优点，虽然也能够保证拼接后目视无缝，但理论不严密，无法保证拼接后影像几何特性。相比之下，物方拼接方法是以卫星相机的严密成像几何关系为理论基础，实现统一几何精度的高品质的拼接影像产品[7-8]。文献[9-10]提出了基于虚拟CCD的内视场物方拼接方法，并分别用日本遥感卫星ALOS的影像和我国“资源三号”（ZY-3）卫星全色多光谱相机影像进行了验证，ALOS和ZY-3的相机探测器间无明显错位。对于探测器间存在明显错位的情况，文献[11-13]采用同样的物方拼接方法，针对ZY-1（02C）卫星和“海洋一号”C/D星影像数据进行拼接，试验表明：当高程起伏大于300m时，将在沿轨推扫方向上引起1个像素以上的拼接误差，即高程误差引起的沿轨方向拼接误差不可忽略。

针对上述问题，同时考虑到弱交会条件下相机间影像拼接问题，若直接采用传统区域网平差模式求解影像间几何配准参数进行拼接处理，会造成平差结果迭代不收敛、连接点处物方高程值解算异常等情况[14]，本文提出一种DEM辅助的物方几何拼接方法。在充分利用影像的定向参数的基础上，构建影像间物方几何配准模型，在平差求解过程中以DEM作为高程约束，克服高程误差引起的沿轨方向拼接误差和弱交会条件引起的迭代不收敛的问题，实现统一几何精度的拼接产品。

1 双相机拼接方法

1.1 定向模型构建

高分辨率遥感相机成像时由于长焦距和窄视场角的特点，接近平行投影。基于严密成像几何成像模型处理高分辨率遥感影像时，虽然理论严密，然而，严密成像几何模型的构建相对复杂，涉及一系列空间坐标系的相互转换，不利于相机影像的几何拼接处理[15]。研究表明利用有理函数模型（Rational Function Model，RFM）进行卫星影像处理，能够达到严密成像几何模型的精度，并且RFM 具有形式简单和计算速度快等优势。因此，本文以高分辨率卫星严密成像几何模型为基础，构建形式简单、易于计算的有理函数模型[16]，并将其作为影像的定向模型，如式（1）所示

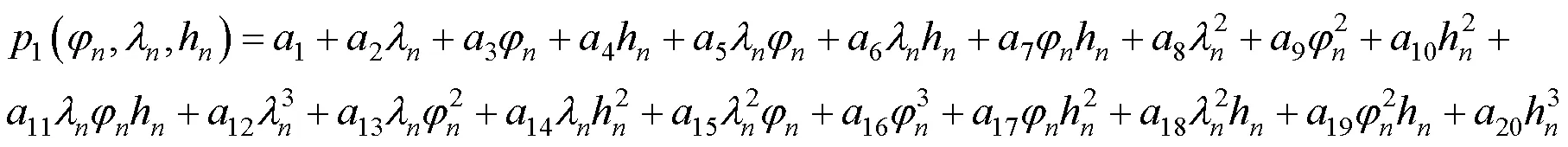
1.2 物方帧间几何配准模型

研究表明以仿射变换、透视变换和刚性变换等传统数学模型作为相机影像间几何配准模型，难以实现统一高精度的几何拼接产品[17]。鉴于此，本文充分利用卫星影像的定向参数信息，以卫星影像的定向模型为基础，构建影像间几何配准模型。事实上，导致卫星相机间影像拼接错位抖动的误差源主要是相机间安装关系变化、卫星平台抖动、相机几何畸变等误差引起的影像间的错位[18]。本文在定向模型的基础上引入影像间几何配准参数，以消除该误差源的影响，以双相机为例，构建的基于卫星影像定向模型的影像间几何配准模型如式（3）所示

1.3 影像间几何配准参数求解

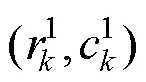
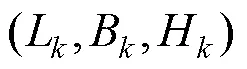
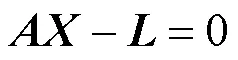
4）按照最小二乘平差原理，求解辅帧相对于主帧的运动参数。

（5）

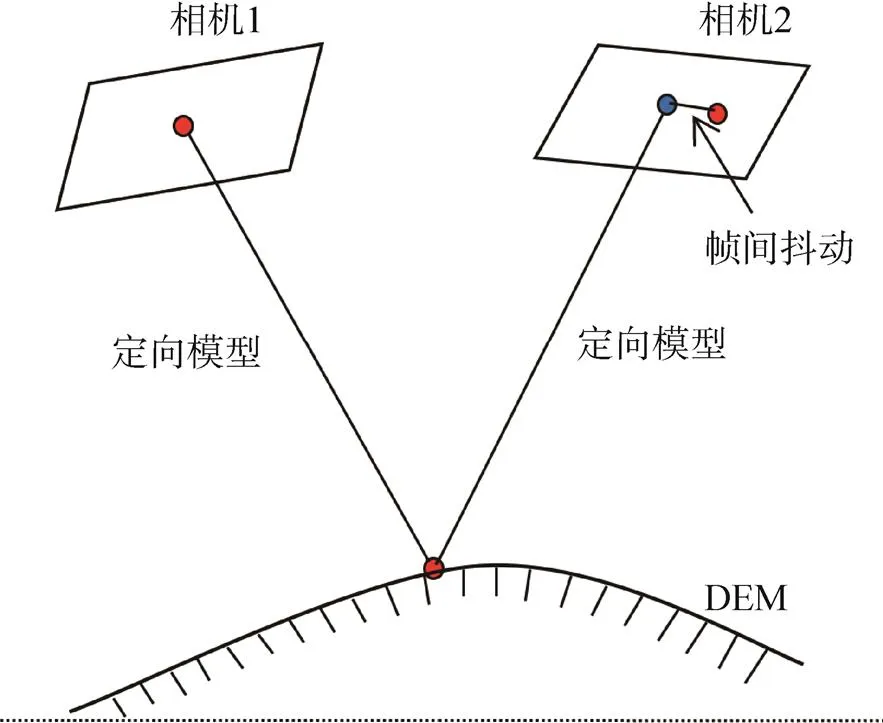
图2 影像间几何配准参数求解示意

1.4 影像几何拼接

求解出影像的几何配准参数后，为便于影像间几何拼接处理，需要对影像的定向参数进行几何配准补偿处理，即：将几何配准参数融合到定向参数中，具体步骤包括：

1）根据影像的原始定向参数构建定向模型，并生成虚拟控制格网点[21]；

2）利用影像的几何配准参数，根据式（3）的第三、四式，对虚拟格网点的像点坐标进行帧间运动补偿；

3）利用步骤2）中的虚拟格网点重新求解影像定向参数，得到几何配准后的定向参数。

2 试验与分析

2.1 试验数据

为了说明本文方法的正确性和有效性，采用GF-2卫星两台相机的1A级标准产品作为试验数据进行试验验证，数据包含影像和RPC参数，相机交会角2.01°，属于弱交会条件。分别选择北京和河南两个试验区数据，北京试验区的范围为东经116.02°～116.48°，北纬39.71°～40.02°，试验区的地貌为平原和山地，高程范围50～600m；河南试验区的范围为东经112.91°～113.37°，北纬34.21°～34.53°，高程范围130～ 1 350m，该测区内均匀布设了21个控制点。

2.2 试验方案设计

为了验证算法的拼接精度，本文选取两个试验区进行试验，试验方案如下：

——试验1：双相机拼接精度试验。采用1m高程精度DEM辅助进行无控制点和有控制点的拼接试验，验证拼接后影像的平面精度。

方案1：采用河南试验区的双相机影像进行无控制点拼接，所有控制点都作为检查点（Check Point，CP）。

方案2：采用河南试验区的双相机影像进行有控制点拼接试验，在试验区均匀选取9个点作为控制点（Ground Control Point，GCP），其余点作为检查点。

对比分析无控和有控条件下连接点处的像方残差，并统计其精度结果。同时通过叠加显示的方法，目视评价拼接后影像接边精度。

——试验2：验证不同高程精度DEM辅助情况下对拼接精度的影响。该试验采用北京试验区和河南验区双相机影像，验证不同高程精度DEM对拼接精度的影响。

方案：采用不同高程精度DEM辅助无控拼接试验，其中格网分辨率分别为1 000m、90m和30m。

2.3 双相机拼接试验

采用试验1中所述的2种方案进行拼接试验，试验结果如表1所示。

表1 有控和无控几何拼接精度

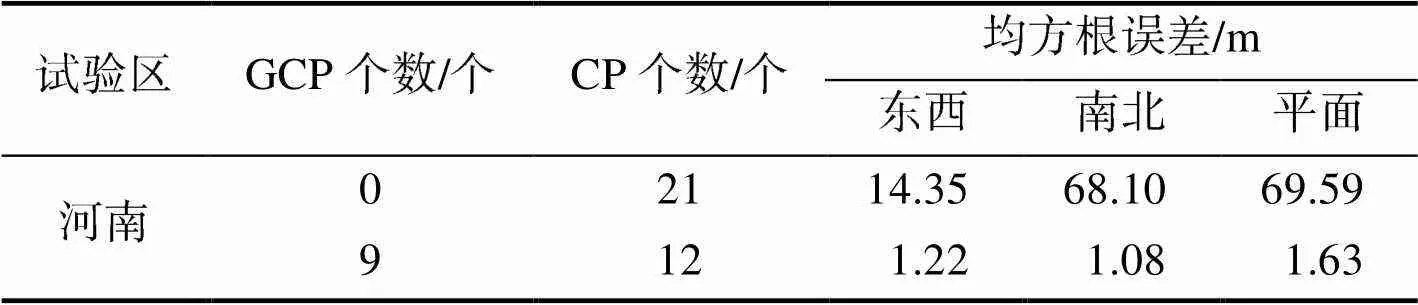
Tab.1 Accuracy of stitching with and without GCPs

从表1的结果可以看出，无控拼接后影像的平面精度为69.59m，采用9点法进行有控拼接精度为1.63m，说明加入控制点后可以有效消除影像绝对定位误差。

为了验证拼接后影像间的接边精度，对每个区域拼接后的连接点（Tie Point，TP）的像方残差进行统计，如表2所示。

表2 连接点试验结果

Tab.2 Results of TPs residual

从表2的结果可以看出，无控拼接方案连接点的中误差在0.5像素的精度水平，有控方案的连接点中误差为0.65像素，比无控方案精度略低，主要是因为在人工量测选取控制点的过程中，量测精度很难达到亚像素，计算影像间几何配准参数时控制点坐标当做真值，精度较差的控制点在平差过程中会影响整个区域网的网型，体现在影像接边处的精度存在略微的下降。两种拼接方式的精度都优于1个像素的精度要求，满足后续产品处理对影像几何品质的需求。

对两台相机影像搭接区进行叠加显示，为了便于目视判读，对两幅影像进行了不同程度的对比度拉伸。图3为河南试验区的拼接效果。可以看出影像接边处精度较好且道路、房屋、高架桥、山区等地形起伏较大的区域均没有出现明显错位现象。目视判读本文方法实现无缝拼接。

图3 河南试验区拼接效果

2.4 不同精度DEM辅助拼接试验

从表3的结果中可以看出，不同分辨率和不同精度的DEM辅助拼接试验，均可以获得一致的平面精度。这是因为GF-2卫星两台相机的几何特性决定的，两台相机交会角仅为2.01°，试验区地形起伏和DEM的高程误差都比较小，引起的物方投影差非常小。试验结果表明，全球1 000m分辨率DEM、90m分辨率，航天飞机雷达测绘使命（Shuttle Radar Topography Mission, SRTM）的DEM[22]和30m分辨率ASTER DEM[23]可以起到同样高程约束的效果，并不会造成拼接精度的下降。若对于侧摆角较大的卫星影像，还是建议采用精度较高的DEM数据作为高程约束。

表3 不同精度DEM辅助拼接精度比较

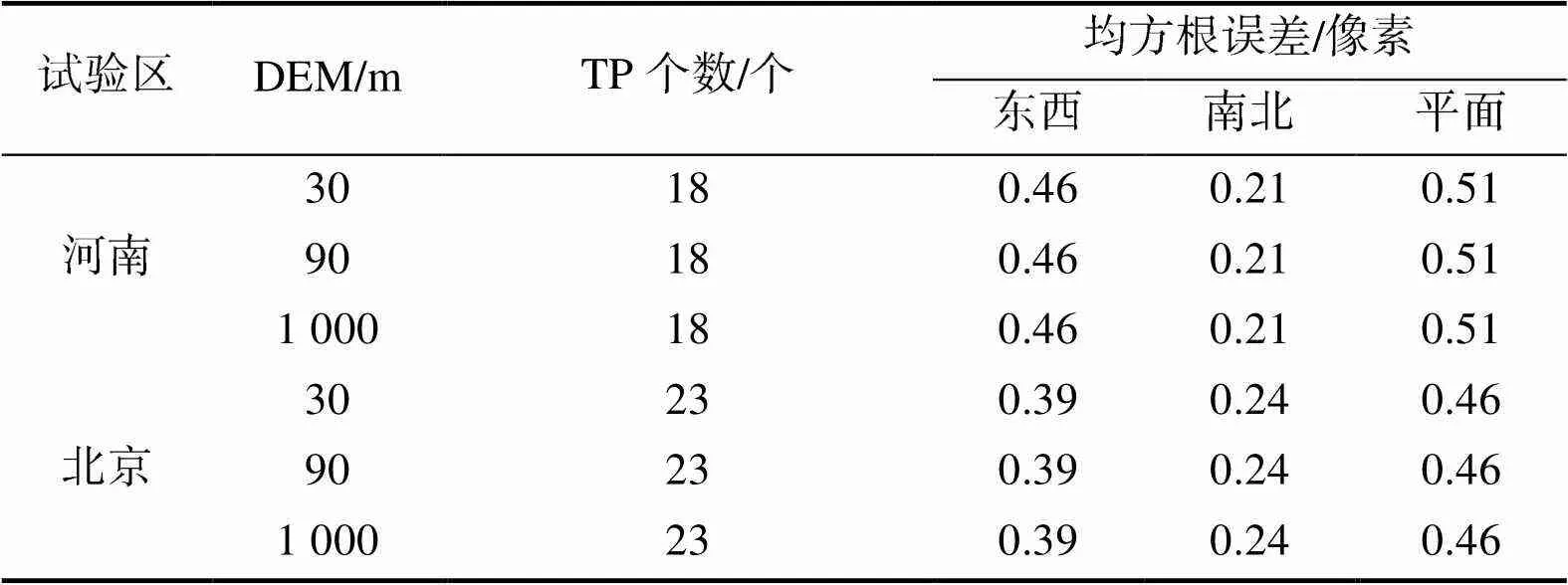
Tab.3 Results of stitching with different DEMs

对两台相机影像搭接区进行叠加显示，为了便于目视判读，对两幅影像进行了不同程度的拉伸。图4为不同高程精度DEM辅助拼接效果。可以看出影像接边处精度较好且道路、房屋、高架桥、山区等地形起伏较大的区域均没有出现明显错位现象。目视评价表明，本文方法能够保证影像的接边处都达到了较高的相对几何精度。

图4 不同精度DEM辅助拼接效果对比

3 结束语

针对弱交会条件下传统拼接方法难以适用的问题，本文提出了一种弱交会条件下物方几何拼接方法，该方法充分利用相机影像的定向参数，以DEM作为高程约束，求解相机间影像几何配准参数，在物方实现影像高精度几何拼接。经对GF-2卫星两台相机影像数据的试验验证，结果表明：本文方法可以实现弱交会条件下相机影像间高精度几何拼接，拼接精度达到了子像素水平，可以满足后续数据应用对几何品质的需求。

[1] 杨秉新, 曹东晶. “高分二号”卫星高分辨率相机技术创新及启示[J]. 航天返回与遥感, 2015, 36(4): 10-15.

YANG Bingxin, CAO Dongjing. The Technology Innovation and Inspiration of GF-2 Satellite High-resolution Camera[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(4): 10-15. (in Chinese)

[2] 樊文峰, 李鸿洲, 温奇, 等. 高分二号卫星影像正射纠正精度分析[J]. 测绘通报, 2016(9): 63-66.

FAN Wenfeng, LI Hongzhou, WEN Qi, et al. Research on Accuracy of Digital Ortho Rectification of GF-2 Image[J]. Bulletin of Surveying and Mapping, 2016(9): 63-66. (in Chinese)

[3] 李德仁, 王密. “资源三号”卫星在轨几何定标与精度评估[J]. 航天返回与遥感, 2012, 33(3): 1-6.

LI Deren, WANG Mi. On-orbit Geometric Calibration and Accuracy Assessment of ZY-3[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 1-6. (in Chinese)

[4] 胡芬. 三片非共线TDI CCD成像数据内视场拼接理论与算法研究[D]. 武汉: 武汉大学, 2010.

HU Fen. Research on Inner FOV Stitching Theories and Algorithms for Sub-images of Three Non-collinear TDI CCD Chips[D]. Wuhan: Wuhan University, 2010. (in Chinese)

[5] TANG X, HU F, WANG M, et al. Inner FOV Stitching of Spaceborne TDI CCD Images Based on Sensor Geometry and Projection Plane in Object Space[J]. Remote Sensing, 2014, 6(7): 6386-6406.

[6] JACOBSEN K, HANNOVER U. Geometric and Information Potential of IRS-1C PAN-images[J]. International Geoscience and Remote Sensing Synposium, 1999(1): 428-430.

[7] CHENG Y, JIN S, WANG M, et al. A New Image Mosaicking Approach for the Multiple Camera System of the Optical Remote Sensing Satellite GaoFen1[J]. Remote Sensing Letter, 2017, 8(11): 1042-1051.

[8] CHENG Y, JIN S, WANG M, et al. Image Mosaicking Approach for a Double-camera System in the GaoFen-2 Optical Remote Sensing Satellite Based on the Big Virtual Camera[J]. Sensors, 2017, 17(6): 1441.

[9] 张过, 刘斌, 江万寿. 虚拟CCD线阵星载光学传感器内视场拼接[J]. 中国图象图形学报, 2012, 17(6): 696-701.

ZHANG Guo, LIU Bin, JIANG Wanshou. Inner FOV Stitching Algorithm of Spaceborne Optical Sensor Based on the Virtual CCD Line[J]. Journal of Image and Graphics, 2012, 17(6): 696-701. (in Chinese)

[10] 唐新明, 周平, 张过, 等．资源三号测绘卫星传感器校正产品生产方法研究[J]．武汉大学学报(信息科学版), 2014, 39(3): 288-294.

TANG Xinming, ZHOU Ping, ZHANG Guo, et al. Research on a Production Method of Sensor Corrected Products for ZY-3 Satellite[J]. Geomatics and Information Science of Wuhan University, 2014, 39(3): 288-294. (in Chinese)

[11] 潘俊, 胡芬, 王密, 等. 基于虚拟线阵的ZY-1 02C卫星HR相机内视场拼接方法[J]. 武汉大学学报(信息科学版), 2015, 40(4): 436-443.

PAN Jun, HU Fen, WANG Mi, et al. Inner FOV Stitching of ZY-1 02C HR Camera Based on Virtual CCD Line[J]. Geomatics and Information Science of Wuhan University, 2015, 40 (4): 436-443. (in Chinese)

[12] CAO J, ZHANG Z, JIN S, et al. Geometric Stitching of HaiYang-1C Ultra Violet Imager with a Distorted Virtual Camera[J]. Optics Express, 2020, 28(9): 14109-14126.

[13] 杨威, 周楠, 曹金山. “海洋一号”D卫星海岸带成像仪双相机几何拼接[J]. 航天返回与遥感, 2021, 42(4): 99-107.

YANG Wei, ZHOU Nan, CAO Jinshan. Double-camera Geometric Stitching of HY-1D Coastal Zone Imager[J]. Spacecraft Recovery & Remote Sensing, 2021, 42(4): 99-107. (in Chinese)

[14] TEO T, CHEN L, LIU C, et al. DEM-aided Block Adjustment for Satellite Images with Weak Convergence Geometry[J]. IEEE Trans. Geosci. Remote Sens, 2010, 48(4): 1907-1918.

[15] GRODECKI J, DIAL G. Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(1): 59-68.

[16] 张力, 张继贤, 陈向阳, 等. 基于有理多项式模型RFM的稀少控制SPOT-5卫星影像区域网平差[J]. 测绘学报, 2009, 38(4): 302-310.

ZHANG Li, ZHANG Jixian, CHEN Xiangyang, et al. Block Adjustment with SPOT5 Imagery and Sparse GCPs Based RFM[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 302-310. (in Chinese)

[17] 张过. 卫星视频处理与应用进展[J]. 应用科学学报, 2016, 34(4): 361-370.

ZHANG Guo. Satellite Video Processing and Application[J]. Journal of Applied Sciences, 2016, 34(4): 361-370. (in Chinese)

[18] 王霞, 张过, 沈欣, 等. 顾及像面畸变的卫星视频稳像[J]. 测绘学报, 2016, 45(2): 194-198.

WANG Xia, ZHANG Guo, SHEN Xin, et al. Satellite Video Stabilization with Geometric Distortion[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 194-198. (in Chinese)

[19] 汪韬阳, 张过, 李德仁, 等. 卫星遥感影像的区域正射纠正[J]. 武汉大学学报(信息科学版), 2014, 39(7): 838-842.

WANG Taoyang, ZHANG Guo, LI Deren, et al. Block Ortho-rectification for Satellite Images[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 838-842. (in Chinese)

[20] LIANG J, GONG J, LI W. Applications and Impacts of Google Earth: A Decadal Review(2006–2016)[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 146: 91-107.

[21] 曹金山, 袁修孝. 利用虚拟格网系统误差补偿进行RPC参数精化[J]. 武汉大学学报(信息科学版), 2011, 36(2): 185-189.

CAO Jinshan, YUAN Xiuxiao. Refinement of RPCs Based on Systematic Error Compensation for Virtual Grid[J]. Geomatics and Information Science of Wuhan University, 2011, 36(2): 185-189. (in Chinese)

[22] CGIAR. SRTM 90m DEM Digital Elevation Database[EB/OL]. [2021-02-14]. https://srtm.csi.cgiar.org/.

[23] 唐新明, 李世金, 李涛, 等. 全球数字高程产品概述[J]. 遥感学报, 2021, 25(1): 167-181.

TANG Xinming, LI Shijin, LI Tao, et al. Review on Global Digital Elevation Products[J]. National Remote Sensing Bulletin, 2021, 25(1): 167-181. (in Chinese)

Dual-camera Images Geometric Stitching Method of GF-2 Satellite

LIU Yang LI Jinxi WANG Chunfa TAN Jian

（No.3 Geology and Mineral Exploration Team, Gansu Provincial Bureau of Geology and Mineral Exploration and Development, Lanzhou 730050, China）

GF-2 satellite uses two cameras to increase the width of the image. In order to improve the efficiency of data use, it is required to provide the stitching products with uniform geometric accuracy. Because of the small overlapping area of dual-camera images and the weak convergence condition, the traditional stitching method is difficult to apply. In this paper, a geometric stitching method of digital elevation model (DEM)-aided block adjustment is proposed. This method takes full advantage of the orientation parameter information of satellite images. A geometric registration model between satellite images based on the rational function model is firstly established. Then, a reference DEM is used as an additional constraint to deal with the weak geometry, the geometric registration parameters for dual-cameras are solved and compensated to achieve the geometric consistency. Our proposed method was tested on GF-2 dual-camera images. The test results show that, under different precision DEM-aided stitching conditions, the proposed method can achieve an accuracy of better than sub-pixel in planimetry and have a seamless visual effect. The test results proved the effectiveness and feasibility of the stitching method.

weak convergence; geometric stitching; Digital Elevation Model; GF-2 satellite; remote sensing application

P236

A

1009-8518(2021)05-0067-09

10.3969/j.issn.1009-8518.2021.05.008

刘洋，男，1987年生，2018年获成都理工大学工程地质专业硕士学位，工程师。主要研究方向为卫星数据处理与遥感地质大数据研究。E-mail：ly_gsdksky@163.com。

2021-03-11

刘洋, 李进喜, 王春发, 等. “高分二号”卫星双相机影像几何拼接方法[J]. 航天返回与遥感, 2021, 42(5): 67-75.

LIU Yang, LI Jinxi, WANG Chunfa, et al. Dual-camera Images Geometric Stitching Method of GF-2 Satellite[J]. Spacecraft Recovery & Remote Sensing, 2021, 42(5): 67-75. (in Chinese)

（编辑：庞冰）