基于BP神经网络模型的股票投资应用
2021-11-10陈婧孙英凡
陈婧 孙英凡




摘要:在全球金融领域中,股票择时投资一直是研究的热点。文章借助BP神经网络模型,结合较全面的影响股价的因素指标,利用主成分分析和计算机挖掘大数据信息的方式,对股票进行择时分析,具有较大的准确性和客观性,对该模型的推广可以弥补我国证券市场的有效性不足问题。
关键词:BP神经网络模型;股票投资
一、引言
近年来,中国资本市场中证券交易发展较为迅速,证券市场价格的剧烈波动给投资者带来巨大的风险。因此,构建基于大数据挖掘技术的股票价格预测模型,对股票投资研究具有深远的意义。当前的研究大多是基于神经网络、决策树、支持向量机等模型研究股票择时问题,但是股票价格的影响因素较多,形成过程复杂,易造成较大误差。所以,本文选择适合处理非线性函数的BP神经网络模型来对股票进行择时研究,相比其他预测方法具有很大的优越性,实现了较好的训练效果,能够为投资者、上市公司和监管部门等提供可靠性依据。
二、BP神经网络模型理论
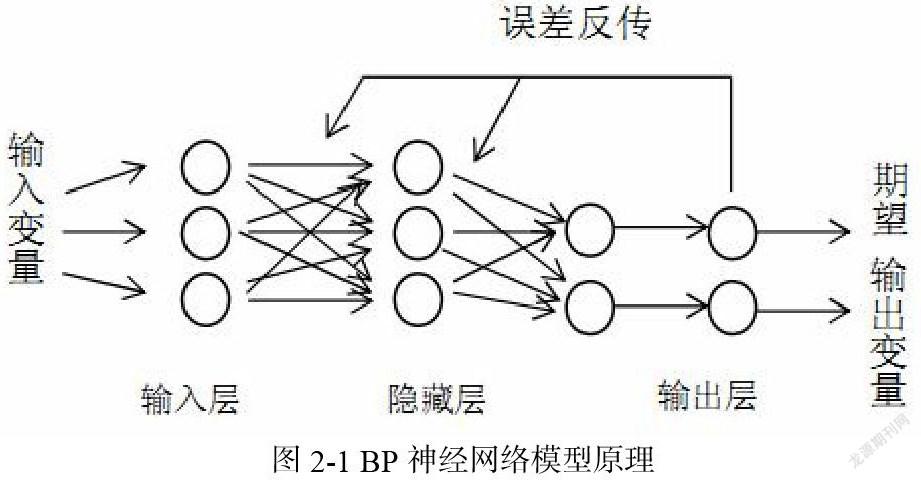
人工神经网络的类型不同是由拓扑结构的差异导致的,常用的前向型网络中就包含BP神经网络模型,它是人工神经网络的经典模型。它的工作原理包括两个部分,即正向数据传输和误差反传校正,如图2-1所示:
在图2-1的正向数据传输中,输入变量从输入层进入神经元,通过权值与阈值的加总计算、激活函数的转换后,将变量储存在隐藏层中;隐藏层的神经元节点再次将变量进行上述运算后,将变量传输给了输出层;输出层的神经元节点会将输出变量与期望输出变量进行对比,将误差反传给输入层,调整权值和阈值,进行第二次的输入输出计算。循环往复,直到输出误差小于期望误差时,输出结果,这时模型的拟合结果会更好地趋向实际值,实现了误差反传校正[1]。
三、BP神经网络模型的构建
(一)BP神经网络模型参数的选取
1.BP神经网络模型输入变量的选择
BP神经网络模型是一种处理非线性、复杂的多维函数的工具,它通过捕捉输入变量与输出变量之间存在的关系进行预测。通过经济学的价值价格理论可知股票价格是由价值决定的,但股票的价值受到多种因素的影响结合而成,故其价格的形成是十分复杂的[2]。通过建模分析市场的相关因素,能够研究股票在市场上的行为,预测股票价格的波动。因此为了模型更加的准确,本文选取了较多的并且经前人总结较为有效的、常用的一些指标,具体介绍如下:
(1)股票的收盘价和开盘价
股票开盘价是证券交易所每个交易日所产生的第一笔交易价格。股票收盘价是证券交易每天交易活动结束前最后一笔交易产生的交易价格。股票前一日的开盘价和收盘价是投资者重要的参考依据,对形成股票价格具有一定影响。
(2)股票的成交量
成交量是指股票在单位时间内成交的交易总量,其与股票价格的发展趋势有很大的关联影响。
(3)股票的最高价和最低价
股市当天的最高价和最低价进行比较,通过比较可以确定开盘价在股价中的地位。股票的最高价和最低价可以反映股价的波动性。其中,可以运用相关数据计算股票的人气指标值,AR 值的计算公式如公式(3.1)所示:
公式中为当日股票交易成交价格的最高价,为当日股票交易成交价格的最低价,为当日股票交易成交价格的开盘价,N为我们设定的参数,通常设定为26日。
2.BP神经网络模型激活函数的选择
神经网络模型的激活函数是指内部处理信息的函数。当输入层的信号进入神经元后,会引起神经元的反应,反应的结果就是神经元激活函数变换的结果[3]。网络中作用很大的激活函数,其对模型解决问题的能力和效率有着很大影响。
S型激活函数是最常用的函数,与另外两种函数不同,S型激活函数是连续可导的。它的输出范围只能为[-1,1]或者[0,1],输入输出关系如公式(3.2)或(3.3)所示:
在建立神经网络模型中,需要激活函数是可导函数,故选择S型激活函数来进行建模分析。
(二)模型构建步骤
1.利用数据进行BP神经网络模型分析
首先对主成分数据和样本进行归一化处理,消除输入变量各维数据之间的数量级差异。数据规范化后,所有数据都可以映射到[-1,1]区间。数据归一化的方法运用的是Min-Max法。选取BP神经网络模型的参数设置模型的输入,4个指标作为神经网络模型的输入变量。将股票的收盘价作为唯一输出变量建立模型。处理后的数据可以作为神经网络模型的输入变量,将股票的收盘价作为唯一输出变量建立模型。建立模型时,选取部分数据作为训练的樣本,另外部分数据作为测试的样本,系统会自动计算利用测试的样本进行模拟后产生的结果。其次设定不同隐藏节点数目,分别进行试验,选择使得误差最小的隐藏节点的数目,就可以得到最优网络。最后将数据进行反归一化[4]。
利用MATLAB建模时,模型的输入变量确定为4个;模型的输出变量只有1个,即股票的收盘价格;模型还需要通过前人总结的试算公式来确定隐藏层的节点数量。普遍被认可的试凑公式如公式(3.4)-(3.6)所示:
公式中q代表输出层中节点的数量,p代表输入层中节点的数量,m表示隐藏层中节点的数量,α则为一个从1至10中含有的常数。在模型建立中,由于有4个输入变量和1个输出变量,所以输入层有4个节点、输出层有1个节点,从而可以确定隐藏层的节点个数的取值范围3-13[5]。虽然无法确定隐藏层节点数,但是可以通过确定的范围多次实验,最后确定最优的节点数量。模型结果得出数据的预测值和真实值两者相对的误差值基本都均控制在2%以下。
为了确定最优的隐藏层节点数量,找到模型的最优情况,继续对隐藏层节点分别为3-13时建立BP神经网络模型,并计算各模型的平均相对误差进行比较。可知,当隐藏层的节点为5时,模型的预测效果最好,并且平均相对误差值较低。因此利用主成分分析和BP神经网络模型是可以追踪上证综合指数走势的。
(三)模型有效性检验
基于之前BP神经网络的模型以及做出的投资决策,需要建立合理的评价指标对该模型的分析结果进行检验。以下是所列举的两个指标:
1.预测值和实际值的均方误差MSE
MSE是指数理统计中参数的估计值与参数的真实值做差平方的期望值。其公式可以表示为:
测量“平均误差”通常采用均方误差这种方法,它可以评价估计值与实际值的拟合程度。公式中求出的MSE值越小,则证明模型预测描述实验的数据精度越好。
2.涨跌研判的准确率
研究和分析次日开盘价“涨”或者“跌”的准确度相对于当日收盘价的百分比是涨跌研判准确度的关键,可以用来衡量本文模型预测的有效性和准确度。因为测试数据的数量是100,所以比较容易能获得近似百分比。
通过此指标判定之前选股方案和投资决策是否与实际情况相符。
四、BP神经网络模型应用及评价
(一)基于BP神经网络模型的预测分析
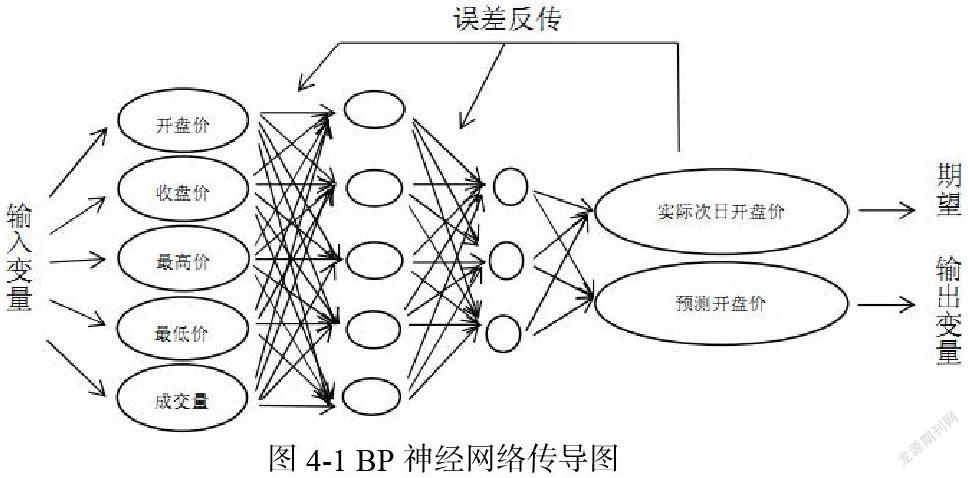
选取从2019年1月29日到2020年3月26日,总共280个交易日的上证股票数据的5个指标,其中包括当日的开盘价、收盘价、最高价、最低价和成交量。借助于K线+成交量的技术分析,通过前200天数据的学习和训练,网络能够自动拟合日开盘价与前一日量价指数的关系,并对未来80天的数据(即79个预测数据)进行次日开盘价的预测,用真实值验证预测的准确性。
选择每日的开盘价、收盘价、最高价、最低价和成交量作为输入,次日的开盘价作为输出,以下是BP神经网络传导过程图[6]:
(二)BP神经网络模型对未来股票市场的预测
利用神经网络模型对现在指数的波动和之后一年指数的波动进行数据预测,由于疫情原因,搜集到的2020年1—2020年3月的数据有可能会含有新冠疫情因素带来的影响,令处于新冠肺炎疫情期间的数据为0,反之为1,以此加入神经网络的训练集中进行预测。若模型研判当日处于“转折”点,那就可推断当天正位于阶段“顶部”,因此可做减仓或做空操作。反之,若股指价格处于下跌的情况下,若模型研判当日处于“转折”点,则可推断当天正位于阶段“底部”,因此可做増仓操作。
从理论上来说,将阶段顶部和底部定义为一个区域更为恰当,从实践的角度来说,微小的差别而导致的仅次于最底部或最顶部的“转折”点仍然具有很强的使用价值和实际意义。鉴于此,如果我们在预测中适当放松对“转折”研判正确的标准,例如定义若模型预测的“转折”点距离实际“转折”只差1个交易日且“转折”点处的最高(最低)价据实际值相差0.5%内,仍然将其计为判断正确。
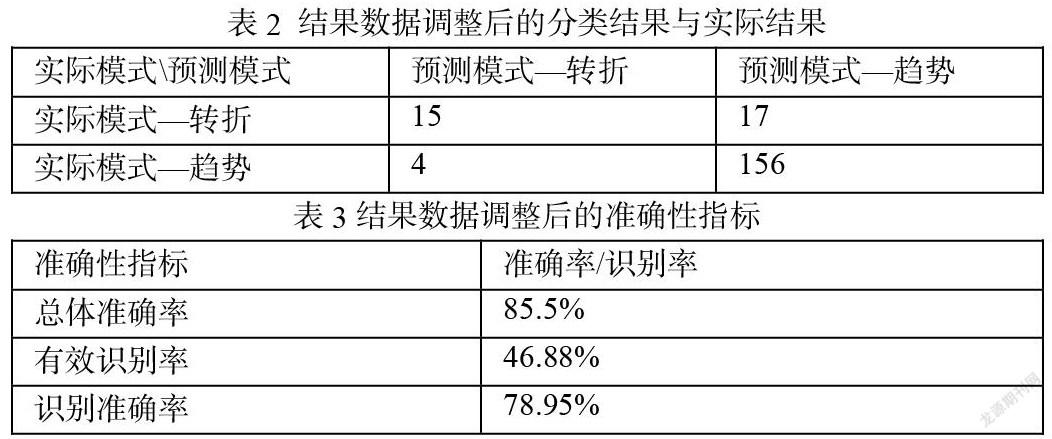
通过这样的调整修正,重新编写程序做统计,得出新的准确性指标如表2、表3所示:
可以发现,股票的风险和回报是可以通过一些特定的参数进行控制的,选股的方案和投资组合的预期收益提供了可以从投资中获得多少回报的估计。风险评估给出投资方在持有此投资的组合时所应该承担的风险估计。投资组合的回报和风险都是取决于股票的回报和风险,及其股票在整个投资组合中的组成份额。根据模型分析得出的结果,可以使投资策略更为科学谨慎,个人获益的概率也会得到相应增加。
五、结论
在实际应用中,若模型研判当日处于“转折”点,那就可推断当天正位于阶段“顶部”,因此可做减仓或做空操作。反之,在股指价格处于下跌的情况下,若模型研判当日也处于“转折”点,则可推断当天正位于阶段“底部”,因此可做増仓操作,从而达到投资收益的最大化。相信本模型未来对于人们投资分析、股东权益最大化和监管层的有效监管都能起到极大的帮助,可以为投资者、监管者和上市公司等提供有迹可循的依据。
参考文献
[1]王霄.基于SVM的沪深300指数量化择时策略实证研究[D].兰州大学,2019.
[2]吴桂雯.量化交易中股票择时的策略研究[D].天津商业大学,2017.
[3]张清洁,钱魏冬.基于量化分析的股票投资策略[J].河北北方学院学报(自然科学版),2020,36(11):50-56.
[4]张筱峰,郭沥阳.沪深300股指期现市场多阶段波动溢出效应研究——基于非对称BEKK-GARCH模型[J].现代财经(天津财经大学学报),2020,40(03):53-66.
[5]刘庆霞.基于主成分分析和BP神經网络的股价预测[D].苏州大学,2017.
[6]赵晨.动态神经网络在量化投资预测中的应用[D],上海:复旦大学,2014:29-30,38-41.
国家级大学生创业训练项目(S202010445081X)
