以数形结合方式，提升解决问题能力的渐进式教学模式研究

吴娜

【摘要】几何直观是《义务教育数学课程标准（2011年版）》中的十大“核心词”之一，主要是指借助图形描述和分析问题，而数形结合是培养学生几何直观能力的重要思想方法，在解决问题时它具有直观、形象、便于操作的特点，学生可不受限制的罗列题目信息，绘图表示数量关系，进而对题目有整体性直观性的理解，提升解决问题能力。笔者将小学阶段的数形结合的教学序列化，探究它对解决问题的帮助，寻求新课改革背景下适合学生思维发展的教学策略。

【關键词】数形结合解决问题新课改

一、提出问题——小学数学在数形结合教学现状分析

（一）用图意识薄弱，关在思路门外

由于低段学生刚开始接触正式的数学，对文字的理解与转化能力较弱，往往会被抽象的题目难倒，教师培养学生的用图意识就显得至关重要，但大多数教师往往忽视学生对数理的理解，单单注重解题技能的训练，使得学生找不到解题思路的钥匙，这对于学生后期解题能力与思维发展是极其不利的。因此必须在低段的时候就对学生进行用图意识的培养，让他们有意识的运用图形来帮助自己理解题意，解决问题。

（二）图和情景分离，偏离解题方向

高段学生的用图意识有所增强，但在“要用图”和“会用图”上还是具有一定的差距，例如在绘图过程中往往会因为对题意的理解错误，关系的表达混乱，或者所画的图与问题情景不能匹配，因此必须对学生进行用图方法的指导。

（三）图形序列缺少，未成画图习惯

数形结合意识的培养，无论是在低段的启蒙教育还是高段的灵活运用都不是一蹴而就的，但大多教师只在解决某一题或某课的难点时进行运用，缺乏系统化、序列化培养，学生也就无法运用零碎的数形结合意识有效解决问题。

二、实践探究——用数形结合方式解决问题的渐进式教学实践

（一）整体规划，让教学更加有序

任何能力的培养都不是一蹴而就的，需要教师对六年的学习进行系统性规划，使教学更有方向与顺序，学生对于每一类解决问题的能力掌握的更加扎实。规划时一定要找到相关的课时，明确该课时培养的能力方面，更要着重于每一课时的之间的练习，力求通过一条主线将不同学段的不同课时联系在一起，循序渐进的教学。

2.承上启下，掌握用图解决问题的方法

学生在低段形成用图意识后，会主动尝试用图解决问题，但是用图技巧的缺失会阻碍解题与思维的发展，因此在中段教师对于方法的传授是非常重要的。

案例分享：《求一个数是另一个数的几倍》和《求一个数的几倍是多少》（如图1、2）是三上的内容，包含了借助象形图和线段图表示数量关系与解决问题，这是学生第一次正式接触选段图，因此笔者在教学中，不是侧重于学生能多快列式解决，而将重点放于“你能用恰当的方式表示出数量关系吗？”“结合图说一说。你是如何表示出题目中的数量关系”，使学生认识线段图，画线段图，学会用线段图来梳理题目中的数量关系。

设计意图：学习了乘法后，学生能将倍数问题转化为“求几个几是多少”和“求几里面有几个几”进行解决，但是如果将思维只局限于语言上的转化，忽视画图表示数量关系，明显会限制学生的发展，只有将数与形结合，将能画图表示数量关系作为一种硬性要求，学生才会形成这种技能，对于之后高段的和倍问题、差倍问题中的数量关系才会信手拈来，并未后面的植树问题、行程问题等打下基础，可以说它是一个承上启下的用图解决问题。

3.自主探索，形成用图解决问题的技巧

低段的“扶”，中段的“帮”，都是为了高段学生能根据问题情景恰当运用数形结合的方式解决问题，因此这时教师要放手，让学生经历尝试、调整，获得自我成长的喜悦。

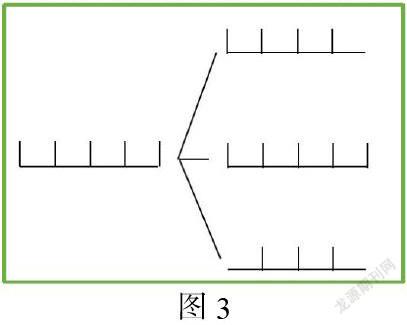
案例分享：热门的《植树问题》是不少老师的公开课首选，植树的教法也各具特色。这个数学广角中包含了“两端都种”、“只种一段”、“一段都不种”和“环形种树”，面对这么多种种法，不少老师以学生掌握植树公式为目标“一边栽一边不栽和环形栽树时，棵树=间隔数，两边都栽时，棵树=间隔数+1，两边都不栽时，棵树=间隔数-1”，但倘若学生只是将公式死记硬背，那么条件稍微一变，学生可能就会蒙圈，所以我将《植树问题》进行整合教学，以线段图贯穿整节课，将课堂时间留给学生自主尝试画图表示各种植树情况上，让学生充分的画、想、说，最终得出结论（如图3）。这时学生心中有图，即使题目再怎么变化，学生都能解答的得心应手。

设计意图：现实生活中类似植树问题的有很多，例如爬楼梯、据木头、画坛摆花、安装电路等，即使学生能将植树公式倒背如流，脑中没有相应的数学模型，依旧不能灵活解决问题。所以面对像植树问题这类问题，应该要用大量的时间培养学生自主用图解决问题，建构同类题目数学模型的意识，提升其思维灵活性。

（三）课时精排，让教学更加有力

1.前测调查学情，了解学生解题思路

五上的解决问题《出租车中的分段计费问题》对于学生是一个理不清且变式更难的问题，它的单价会随路程的变化而浮动，打破了学生固有的解题思路，且学生缺少这类生活经验，面对复杂的题干，往往找不到对应的数量关系，也就无从下手。

前测作为一种有效了解学情的手段，能帮助老师掌握学生已有的知识与技能，从而规划教学重难点。以下是笔者给学生的设计的前测题组，了解学生对数量关系的应用情况：

前测结果：前测一共测评了3个班118人，全对的只有35人，失分率高达70.34%，针对这83人进行了错误分析：

由此可见，对于学生来说抽象的数量关系是学生理解的薄弱点和解题思路的盲区，如果能让学生通过图形的表征，将各区间的计费数量与区间的计费标准意义对应，就能有效提升学生解读信息的能力。

3.练习拓展提升，促进学生灵活运用

如果例题对学生而言是房子的地基，那么接下来砖的选择就非常重要，笔者选取了生活中常见的分段计费的例题进行分类与设计如下：

（1）某快递公司的计费标准如下，1～11千克0.5元/千克，11～21千克1.5元/千克，21千克以上2元/千克。王阿姨现在有一个重30千克的货物，请问她要付多少钱？

（2）温州市某公共自行车收费标准如下：

三、小结

华罗庚教授曾以精辟而又通俗的语言阐明了数和形结合的必要性“数无形而少直观、形无数而难人微，数形结合百般好、隔裂分家万事休”。数形结合思想让复杂的问题简单化，抽象的问题具体化，不仅提升了小学生的数学学习素养，更为他们将来学习复杂的数学知识甚至是终身学习和可持续发展打下有益的基础。因此，作为教师我们更应当深挖知识背后的数形结合思想，在日常教学中系统化、序列化渗透思想。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011 年版）[M]. 北京：北京师范大学出版社，2012.

[2]梁淑颖.寻问题根源，觅解题佳径——“分段计费”错因分析与再思考[G].基础教育，2019（8）：69-70.