增材制造中滚筒铺粉工艺参数对尼龙粉体铺展性的影响研究1)

2021-11-10张江涛谭援强纪财源肖湘武姜胜强

力学学报 2021年9期

张江涛谭援强 ,2) 纪财源肖湘武姜胜强

* (华侨大学制造工程研究院,福建厦门 361021)

† (湘潭大学机械工程学院,湖南湘潭 411105)

引言

基于粉床的增材制造(additive manufacturing,AM)技术在工业上被广泛应用[1-2],铺粉工艺是该增材制造技术的关键工序之一[3-4],铺展出平整均匀的高密度粉床是制备优良性能零件的前提条件.在薄层粉末(粉层厚度通常在200 μm 以下)的铺展过程中,由于微米级颗粒的粘附团聚和堵塞[5],造成粉床的均匀性和密度较差,并导致零件表面精度低和内部孔隙等问题的出现[6].

粉体的铺展性与粉体的流动性紧密相关但又不同[7-8].粉体流动性的定义在学术界并未统一.目前运用较多的粉体流动性的表征方法有:休止角法[9]、质量流率法[10]、Hausner 指数法[8]、剪切法[11]等.休止角法和质量流率法适用于自由流动的粉体,由于增材制造粉体粒径一般小于100 μm,而粉末粘附和粉末对壁面的摩擦导致粉末很难流过流量计的小孔[8].因此,休止角法和质量流率法不适用于增材制造粉体的流动性表征.FT4 粉体流变仪[12]和Revolution粉体分析仪[13]可以表征粉体在动态条件下的流动性,在一定程度上有助于了解粉体的动态流动行为.但是,粉体的流动行为取决于其颗粒特性(粒径分布、颗粒形状和颗粒表面纹理)和外部条件(环境湿度、温度和应力条件).而现有的测试方法不是针对薄层粉体铺展过程的,使得它们难以精确预测AM过程中的粉体铺展性[14].

近几年,粉体流动性和粉体铺展性的测量和定量表征已被确定为增材制造的关键技术.Snow 等[15]尝试建立粉体铺展性指标,研究表明覆盖率、沉积速率和雪崩角变化速率可定量评估粉体的铺展性.Cordova 等[16]通过测量粉层密度来表征粉体的铺展性.然而,铺粉实验耗时且需要消耗大量昂贵的粉体材料,也难以深入揭示粉体铺展过程的微观机理.离散元法(discrete element method,DEM)在模拟颗粒物质运动方面具有独特的优势[17-18],已被用于模拟增材制造铺粉过程[19-23].国内外学者从颗粒动力学[19-20]、粉床质量[21-22]以及铺粉器的结构优化[23]等方面揭示铺粉过程的物理机制.针对粉体铺展性的研究,Ahmed 等[19]通过测量粉层空斑来评估粉体的铺展性,DEM 仿真和实验图像分析的结果吻合良好.

粉体的铺展性指标可分为粉层质量(粉层密度、覆盖率和空斑)和粉体流动形态(沉积速率和雪崩角变化率).Escano 等[24]通过X 射线成像研究了粉体铺展过程中的颗粒动力学行为.研究表明在粉体铺展过程,雪崩角几乎没有变化,而这与Snow 等[15]的研究结果相矛盾.粉体铺展性不仅与粉体的粒径粒形有关,而且与铺粉工艺参数密切相关.铺粉器的结构和速度都会影响粉体的铺展性[5,15].但是,铺粉工艺参数对粉体铺展性的影响研究相对较少.滚筒铺粉工艺参数包括铺粉层厚、滚筒直径、滚筒的旋转速度和平移速度[3,5].滚筒的铺粉工艺参数相对复杂,通过经验和繁琐的实验来优化铺粉过程是不可取的.因此,有必要优化滚筒铺粉工艺参数来提高粉体的铺展性.随着优化方法的发展,响应曲面法(response surface methodology,RSM)和遗传算法等智能算法被用于优化参数以解决工程问题[25].RSM方法通过多项式拟合因子和响应之间的关系,分析单因素和交互因素对响应指标的影响,并获得最佳参数,是一种可靠且有效的优化方法.

本文采用DEM 模拟尼龙粉末的滚筒铺展过程.选择铺粉层厚、滚筒直径、滚筒旋转速度和平移速度作为变量因子.建立沉积分数、覆盖率和沉积速率3 个铺展性指标.采用中心复合设计(central composite design,CCD)生成30 组案例,建立3 个指标的回归模型.根据方差分析(analysis of variance,ANOVA),确定单因素及交互作用对响应指标的影响.最后,以铺展性指标为优化目标,进行了滚筒铺粉参数的多目标优化,并通过实验验证了优化结果.本研究有助于优化滚筒铺粉工艺参数以提高粉体铺展性.

1 研究方法

1.1 离散元模型

在DEM 模型中,颗粒有两种运动,即平移运动和旋转运动,根据牛顿第二运动定律来描述颗粒的运动方程[26]

Hertz−Mindlin 接触模型考虑了颗粒接触力[27],而JKR (Johnson−Kendall−Roberts)理论在Hertz−Mindlin 接触模型的基础上考虑了接触区域内的黏附力[28]

式中R∗,E∗,γ 和α 分别是等效半径、等效杨氏模量、表面能密度和接触半径.

接触半径 α 和法向重叠 δn之间的关系为[29]

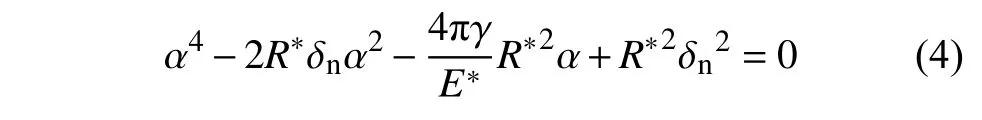
根据式(3)和式(4),即使颗粒非接触时,黏附力仍然存在.JKR 模型提供了颗粒间非接触状态下黏附力的计算方法.颗粒之间的临界间隙 δn,c和临界接触半径 αc通过下式计算[28]

当颗粒之间的间隙大于临界间隙时,黏附力为零.当颗粒未接触且间隙小于临界间隙时,JKR 模型提供了黏附力的最大值Fpullout,其计算公式为[28-29]

关于JKR 接触模型的信息详见参考文献[28-29],为了简洁起见,本文不予赘述.

1.2 铺粉工艺模型

尼龙粉末是选择性激光烧结(selective laser sintering,SLS)中广泛使用的材料.本文所用尼龙粉末为湖南华曙高科技有限责任公司产品(PA3300).在测试粉体有关参数前,将尼龙粉末放在80 °C 的真空炉中干燥12 h.通过动态颗粒分析仪(德国莱驰科技有限公司,Retsch Camsizer X2)测量颗粒的粒径分布,测得粒径D50为49 μm,如图1 所示.使用扫描电子显微镜(日本电子科技有限公司,JSM-IT500LA)观察粉末的微观形态,如图2 所示.从图2中可以看出尼龙颗粒是近球形的.因此,在DEM 仿真中将尼龙粉末简化成球形颗粒.DEM 参数包括物性参数(颗粒密度、杨氏模量、泊松比和表面能)和接触参数(静摩擦系数、滚动摩擦系数和恢复系数).DEM模型参数的选取详见参考文献[30-31],仿真中的DEM 模型参数如表1 所示.如图3 所示,滚筒铺粉模型包含滚筒、送粉缸和基板.送粉缸和基板的宽度和长度均为3 mm 和18 mm.由于Y方向上颗粒的流动对模拟结果的影响很小,因此在Y方向的两侧设置周期性边界条件,以降低计算成本.首先,产生100 000 个颗粒,在送粉缸的上面形成粉床.其次,滚筒沿X轴的正方向以平移速度V并逆时针旋转运动形成铺粉层(第一层粉末).送粉缸上升一个铺粉层厚H,而基板下降一个相同的铺粉层厚H.最后,滚筒再次沿X轴的正方向并逆时针旋转运动形成铺粉层(第二层粉末).

图1 尼龙粉末的粒径分布Fig.1 Particle size distribution of nylon powders

图2 尼龙粉末的微观形貌图Fig.2 Micro topography of nylon powders

表1 仿真中的DEM 参数Table 1 DEM parameters in simulation

图3 滚筒铺粉过程的DEM 模拟Fig.3 DEM simulation of roller-spreading processes

1.3 可铺展性指标

本文采用沉积分数、覆盖率和沉积速率3 个指标来量化评价粉体的可铺展性.在SLS 工艺中,通过逐层铺粉、逐层扫描烧结的方式直接制造零件.只有第一层粉末铺展在上基板,而后续的粉层铺展在先前的粉层上.激光每次烧结一层粉末,因此只关注单层粉末的铺展性.故而本文所建立的指标是基于第二层粉末.采用粉层的沉积分数表征粉层密度,沉积分数φ的计算公式为

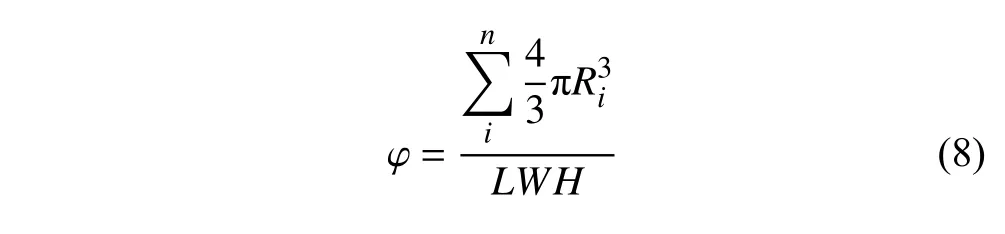
式中,Ri为颗粒i的半径,L和W为基板的长度和宽度,H为铺粉层厚,n是第二层铺粉中颗粒的总数量.

当铺粉完成后,第一层粉末和第二层粉末分别标记为蓝色和橙色,如图4 所示.根据图像灰度阈值计算蓝色和橙色像素的面积[32].橙色像素与蓝色和橙色像素之和的比值定义为覆盖率

图4 第一层粉末和第二层粉末分别被标记为蓝色和橙色Fig.4 The first and the second powder layer are marked by blue and orange colors,respectively

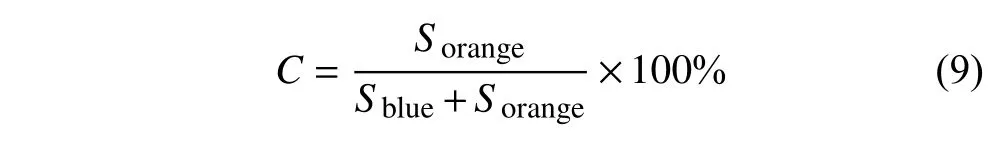
式中,Sblue和Sorange分别是第一层粉末和第二层粉末的像素面积.

粉末铺展过程中,在滚筒的前面会形成粉堆.铺展过程分为粉末积累阶段和粉末沉积阶段.如图5所示,粉末累积阶段对应于滚筒的初始移动阶段,粉末不断在滚筒前面累积.粉末沉积阶段对应于滚筒的持续移动阶段,粉末连续沉积在粉床上,粉堆的面积随滚筒的移动不断减少,如图6 所示.在最后阶段,由于粉堆被推出计算域,粉堆的质量会随着滚筒的移动而显著降低.忽略最后阶段对沉积速率的影响,粉末沉积速率定义为

图5 粉堆的质量随滚筒在X 方向上位移的关系Fig.5 Mass of the powder pile as a function of roller’s displacement in the X direction

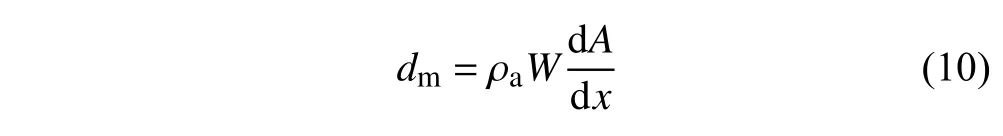
式中,ρa粉堆的表观密度[33],dA/dx是粉堆面积随滚筒在X方向上位移的变化率.dm表征了滚筒前面的粉堆质量随滚筒在X方向上位移的变化速率.

1.4 响应曲面法

由Box 和Wilson[34]提出的RSM 是一种优化随机过程的统计方法,在因子和响应指标之间拟合多元回归方程来探索响应指标和因子之间的定量规律.通常,二阶多项式获得的回归方程可用于分析和优化多元问题,其定义为[35]

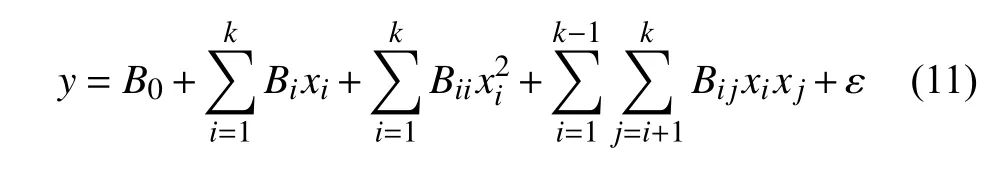
式中,y,B0,Bi,Bii和Bij分别是响应项、常数项、线性系数、二次项系数和交互项系数.k,xi和ε分别是变量数、输入因子和随机误差.

根据文献[3,5] 和实际工程中滚筒的铺粉工艺参数,选择铺粉层厚H,滚筒直径D,滚筒的旋转速度ω和平移速度V作为变量因子.因素和水平如表2所示.采用RSM 的CCD 模型生成30 个案例.沉积分数φ、覆盖率C和沉积速率dm的响应指标可通过方程式(8)～式(10)计算,响应指标的结果如表3所示.

表2 响应面分析因子及水平表Table 2 Response surface analysis factors and levels

2 结果和讨论

2.1 方差分析和回归模型

根据表3 的数据,对获得的数据进行方差分析和拟合回归方程,通常认为P值小于0.05,F值较大则表明该模型显著,R2预测值越接近于1,表示模型预测性越好[35].采用Design-Expert 软件对3 个响应指标和因子之间的回归模型进行分析,得到3 个指标的回归方程

沉积积分数、覆盖率和沉积速率模型的ANOVA 结果如表4 所示.3 个模型的P值均小于0.0001,且3 个模型的F值均有效,表明这3 个模型是显著的.3 个模型的R2预测值都大于0.80,表明这3 个模型具有良好的预测能力.

表4 回归模型的方差分析Table 4 Variance analysis of regression models

2.2 铺粉工艺参数对粉体铺展性指标的影响

根据方差分析和回归方程中因素系数的大小,参数H,D,ω,V,HV,DV,H2,D2和V2对沉积分数有重要影响,参数H,ω,V,HV,H2和V2对覆盖率有重要影响,而参数H,D,ω,V,HV,DV,D2和V2对沉积速率有重要影响.在4 个影响因素中,H是最大的影响因素,V是次要的影响因素,D和ω对粉体铺展性指标影响较小.HV和DV的交互作用对粉体铺展性指标具有重要影响,而其他交互作用影响则可以忽略不计.因此,将进一步分析这些因素对粉体铺展性指标的影响.

当D为20 mm,ω为150 r/min 时,HV对粉体铺展性指标的影响如图7 所示.随着铺粉层厚的增加和平移速度的降低,φ，C和dm的值显著增加.铺粉层厚和平移速度与沉积分数、覆盖率和沉积速率呈二次抛物线关系,这表明铺粉层厚与平移速度之间存在交互作用.3 个指标从粉层质量(沉积分数和覆盖率)和粉末流动形态(沉积速率)的角度揭示了粉体铺展性.通常,较高的沉积分数、覆盖率和沉积速率意味着良好的铺展性.当铺粉层厚较小时,由于机械拱起和颗粒堵塞[4,22],颗粒难以通过滚筒与粉床之间的间隙,导致3 个指标值减少.穿过滚筒与粉床之间间隙的颗粒由于其惯性将移动一定距离[22],最后沉积在粉床上形成铺粉层.当平移速度增加时,穿过间隙的颗粒速度会增加,导致颗粒移动更长的距离,造成沉积在粉床上的颗粒数减少,导致较差的粉体铺展性.这与文献[5] 的研究结果相一致,表明本文研究结果的可信度.

图7 H−V 相互作用对粉体铺展性指标的影响(D=20 mm 和 ω=150 r/min)Fig.7 Interaction effect of H−V on powder spreadability indicators(D=20 mm 和 ω=150 r/min)

当铺粉层厚较高且平移速度较低时,沉积分数和沉积速率值较大.在低铺粉层厚下,覆盖率随平移速度的降低而增加.但是,当铺粉层厚在180−200 μm时,平移速度对覆盖率影响很小,因为覆盖率已经接近饱和值100%.表3 中覆盖率的R2预测值为0.899 0,预测精度小于其他两个指标,主要是由于在较大铺粉层厚下,覆盖率接近饱和值100%.此时,该指标将失去判别精度.

当铺粉层厚较大时,覆盖率的判别精度较低,因此回归模型中DV对覆盖率的影响并不显著.当H为150 μm,ω为150 r/min 时,DV对沉积分数和沉积速率的影响如图8 所示.从等高线图可以看出因素之间的相互作用.当滚筒的平移速度较高时,沉积分数和沉积速率两个指标随滚筒直径的增加而增加,但此时平移速度和滚筒直径之间的相互作用比较微弱.在较低的滚筒平移速度下,轮廓线几乎是椭圆形的.表明平移速度和滚筒直径之间的相互作用是显著的.当滚筒直径范围为15−22 mm 时,指标可以达到较大值.文献[3] 的研究也表明,在一定范围内增加滚筒直径,会加强滚筒对粉末的压实效应,从而提高粉体的铺展性.

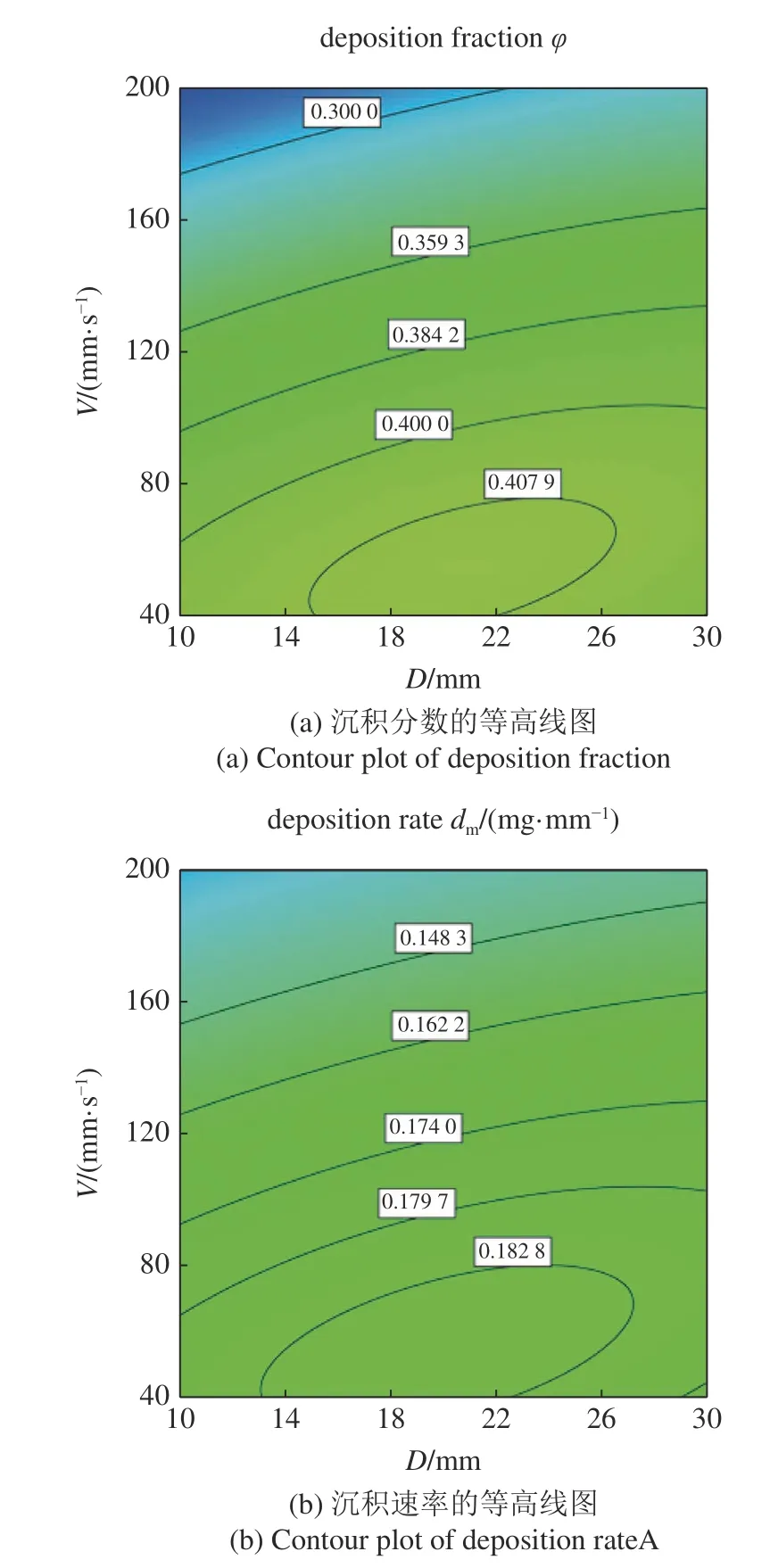
图8 D−V 相互作用对粉体铺展性指标的影响(H=150 μm 和 ω=150 r/min)Fig.8 Interaction effect of D−V on powder spreadability indicators(H=150 μm 和 ω=150 r/min)

2.3 多目标优化

滚筒铺粉工艺参数非常复杂,且参数之间的相互作用也会影响粉体的铺展性.因此,有必要通过整合多个铺展性指标来获得最佳的滚筒铺粉参数组合.由Derringer 和Suich[36]开发的期望值法被用于多目标优化,该方法以响应变量的满意程度为基础,将估计的响应变量转化为满意度函数[36]

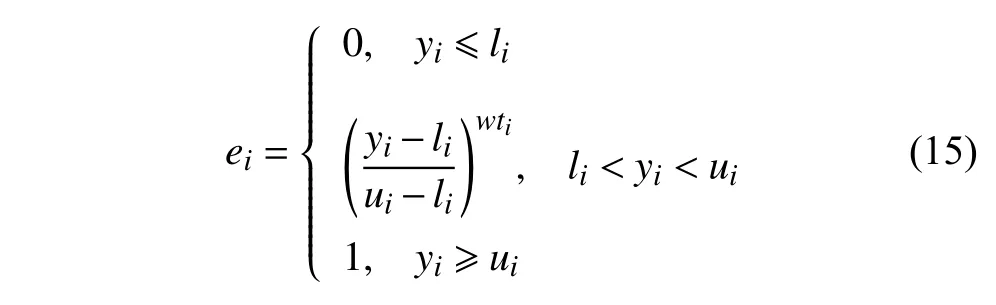
式中,yi是响应变量,ui和li分别为响应的最大值和最小值,wti为权重.

在建立单个响应满意度函数的基础上,构造总体满意度函数来衡量所有响应的总体满意度[36]

式中,ei是每个响应的期望值,ri是ei的权重,N是响应的数量.

参数的取值范围都在表2 的设计范围内,3 个指标具有同等的重要性.在Design-Expert 软件将沉积分数、覆盖率和沉积速率设置为最大值,使用期望值法,获得了预测的最优参数组合和最优指标组合.最佳参数组合:铺粉层厚H为198 μm,滚筒直径D为22 mm,滚筒的旋转速度ω为64 r/min,平移速度V为135 mm/s.预测的最佳指标:沉积分数、覆盖率和沉积速率分别为0.444 0,98.40%和0.266 0 mg/mm.

3 实验验证

采用湖南华曙高科技有限责任公司的HS403P设备进行沉积分数实验.首先,使用最常见的激光参数烧结9 个15 mm × 15 mm × 15 mm 的尼龙实验包,壁厚为2 mm,如图9 所示.考虑到粉末会粘附在实验包的内表面,很难将粉末完全收集.因此,用精密天平(分辨率0.01 mg)称量装有粉末的实验包.然后,除去实验包中的粉末,并超声清洗实验包.最后,通过精密天平称量实验包.通过粉末和实验包的质量之和减去实验包的质量可以获得粉末的质量.沉积分数的计算公式为

图9 用于测量沉积分数的实验包Fig.9 Experimental packages for measuring deposition fraction

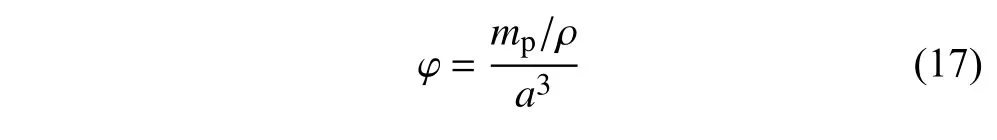
式中,mp是实验包中尼龙粉末的质量,ρ是尼龙粉末的材料密度,a是实验包的边长.

由于在商用设备中难以在线监测粉体的铺展过程,因此,基于SLS 设备的铺粉装置搭建铺粉实验平台,如图10 所示.铺粉实验平台包括送粉缸、成型缸和滚筒.送粉缸上升一个铺粉层厚,而成型缸下降一个相同的铺粉层厚.缸的上下运动由伺服电机控制.滚筒的直径为22 mm,滚筒沿X轴的正方向以平移速度V并逆时针旋转运动形成铺粉层.

图10 铺粉实验平台Fig.10 Powder spreadability device

由于相同颜色的粉末将无法区分像素.因此,在开展覆盖率的铺粉实验中,第一层粉末是白色尼龙粉末,第二层黑色尼龙粉末.白色和黑色尼龙粉末来自同一生产厂家,具有相似的材料特性,只是颜色不同.将摄像机(杭州海康威视数字技术股份有限公司,MVLMF2528M)固定在基板上,并从正上方拍摄粉层的表面形态,如图11 所示.通过灰度处理和阈值分割,使图像变为黑白二值化图像.最后,计算黑色和白色像素的面积,黑色像素与黑色像素和白色像素之和的比值作为覆盖率.

图11 覆盖率的实验方法Fig.11 Experimental method for percent coverage

为了监测铺粉过程的流动形态,将微型摄像头(中国台湾安鹏科技股份有限公司,AM7013MZT)安装在滚筒支架的侧面,并随滚筒在X方向上移动.将微型摄像头调整到合适的位置和放大倍数.在每次实验中,采集铺粉过程的粉体流动形态,如图12 所示.采集粉体不同时刻的流动形态,根据图像分割法计算粉堆的面积[37],然后根据式(10)计算沉积速率.

图12 铺粉过程的粉末流动形态Fig.12 Powder flow pattern during powder spreading

为了减少实验误差,将每个指标的实验重复9 次以获得平均值.沉积分数、覆盖率和沉积速率的实验平均值分别为0.416 1,94.12%和0.282 3 mg/mm,具体结果如表5 所示.沉积分数、覆盖率和沉积速率的预测结果与实验结果之间的误差分别为6.28%,4.35%和6.13%.误差在合理范围内,表明所建立的预测模型是可信的.