基于滑模变结构制导律的捕获区分析
2021-11-10李万礼雷虎民骆长鑫李世杰
李万礼, 李 炯, 雷虎民, 骆长鑫, 李世杰
(1.空军工程大学防空反导学院, 陕西 西安 710051; 2.空军工程大学研究生院, 陕西 西安 710051)
0 引 言
临近空间高超声速武器作为军事领域的新型战略力量,具有飞行速度快、打击范围广等特点,能突防目前几乎所有的防御体系,对空天安全构成极大威胁[1-3]。拦截高超声速目标不同于传统目标,拦截弹将失去速度优势,为了实现对目标的有效拦截,需确保拦截弹顺利完成中末制导交接班,并使得拦截弹处于有利的拦截阵位,即末制导律的捕获区[4]。捕获区不仅提供了中制导弹道终端约束条件,而且还决定了拦截弹能否在末制导起始时刻具有较好的拦截姿态[5-6]。
目前,国内外学者对捕获区的研究主要集中在比例导引及其各种改进形式上。文献[7-10]对几种常见的比例导引律进行了研究,成功推导出了比例制导律的捕获区并进行了验证,但其推导过程极其复杂。文献[11-12]利用微分几何理论,得到了描述真比例导引的捕获区相平面图,但该图比较抽象,与实际飞行参数很难对应起来,难以进行理论分析。文献[13]对纯比例导引制导律及反比例导引制导律的捕获区分别进行了较为系统的分析,然而在非惯性坐标系下的研究结论并没有普遍的适用性。文献[14]在顺轨和逆轨的零控拦截条件基础上,推导得到了比例和反比例导引律的捕获区以及各自导航比设置范围,但是对零控拦截条件的分析过于简单。文献[15-16]提出一种拦截末端攻击区的建模方法,并在此基础上利用空间几何关系推导得出了拦截弹的捕获区,但该推导过程未针对某一特定的末制导律,难以设计出一种适用于该情形的末制导律。文献[17]针对中末制导交接班时刻拦截弹状态约束设置的问题,分析得到了真比例导引静态以及动态捕获区,然而缺乏对目标速度前置角约束范围的严密推导。文献[18-19]分别在不考虑和考虑拦截弹饱和过载限制情况下,对现实真比例导引律的捕获区域进行分析,但是推导过程复杂,难于在工程上应用。
由以上文献可知,现有捕获区的研究主要围绕经典制导律展开,缺乏针对现代制导律捕获区的研究。然而,很多基于现代控制理论的末制导律已经逐渐开始应用到武器的研发设计中,例如微分几何制导律[20-21]、最优控制制导律[22-23]、滑模变结构制导律[24-26]等。现代制导律的制导性能优良,若应用到反高超声速武器作战中,会极大提高拦截概率,研究现代制导律的捕获区将为拦截弹中制导弹道设计提供强约束条件,具有重要意义。
针对现有捕获区研究的不足,本文基于滑模变结构控制理论,设计了一种能够保证拦截末端过载收敛且性能优良的滑模变结构制导律作为末制导律,结合末制导弹目相对运动关系求解出了零控拦截条件,并得出了目标速度前置角的约束范围,给出了滑模变结构制导律的捕获区定义,并推导得到了捕获区的边界条件,将捕获区的研究拓展到现代制导律,为中末制导交接班状态约束设计提供了理论支撑。
1 弹目相对运动模型建立
1.1 基本假设条件
临近空间高超声速目标的飞行速度一般在5马赫以上,而拦截弹通常以迎面拦截的方式对其防御,故弹目相对速度会很大,使得末制导时间很短,则可忽略弹目受到的重力和空气动力的影响[27-29]。从临近空间高超声速目标的整体轨迹来看,其滑翔段机动过载相对较小,在末制导有限的距离和时间内,可忽略目标机动的影响[30]。
结合以上分析,作出假设如下:
假设 1将拦截弹与目标视为质点,忽略重力以及空气动力对拦截弹与目标的影响;
假设 2导引头的最大作用距离记为Rmax,当拦截弹接近目标至导引头的最大作用距离时,则认为目标被导引头成功探测并捕获;
假设 3末制导阶段时间较短,忽略目标机动和重力的影响,过载指令不影响拦截弹的速度大小,只改变速度方向;
假设 4拦截弹的速度始终小于目标的速度,即目标与拦截弹的速度比ρ=‖VT‖/‖VM‖>1。
1.2 弹目相对运动分析
结合基本假设条件,拦截弹与目标在垂直平面内的相对运动关系如图1所示。
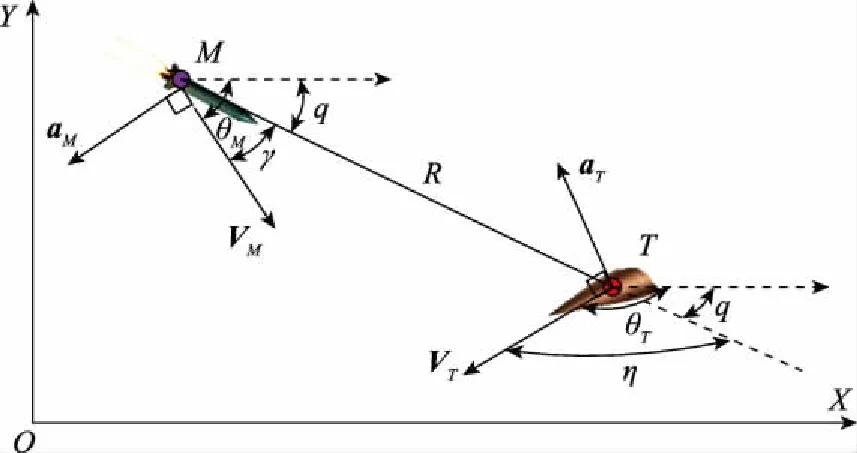
图1 弹目相对运动关系
建立地面惯性坐标系XOY,M表示拦截弹,T表示目标,MT表示弹目视线(line of sight, LOS),R表示弹目相对距离,q表示视线角,VM和VT分别表示弹目的速度矢量,aM和aT分别表示弹目的加速度矢量,θM和θT分别表示弹目的弹道倾角,γ和η分别表示弹目的速度前置角。
通过分析图1中的几何关系,得出拦截弹与目标的运动方程以及相对运动方程:
(1)
(2)
(3)
γ=q-θM
(4)
(5)
(6)
(7)
η=q-θT
(8)
(9)
(10)
其中,(XM,YM)和(XT,YT)分别表示拦截弹和目标在地面惯性坐标系下的位置。
2 滑模变结构制导律设计
2.1 制导律设计
根据滑模变结构控制相关理论,设计一种高性能且能保证末端过载收敛的滑模变结构制导律,过程如下:
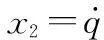
(11)
式中:u=|aM|为控制量。
为了确保拦截弹能够准确命中目标并使得拦截弹需用过载尽可能小,借鉴平行接近法的原理,可以通过设计制导律使得视线角速率趋近于0。故选取切换面如下:
(12)
为确保滑模变结构制导律的鲁棒性,构造对时变参数具有自适应能力的变结构趋近律:
(13)

将式(12)代入式(13)得
(14)
再结合式(11)可得
(15)
2.2 稳定性分析
选取如下Lyapunov函数:
(16)
对式(16)求时间的一阶导数:
(17)
将式(11)和式(15)代入式(17)得
(18)
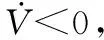
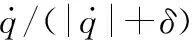
(19)
式中:δ>0为待设计参数,代表着高增益连续函数接近sgn(S)的程度,一般取值较小。
3 滑模变结构制导律捕获区研究
3.1 零控拦截条件分析
定义 1在末制导中,当拦截弹状态达到零控拦截条件时,拦截弹可以在有限时间内仅经过一段无控滑翔之后成功拦截目标。
定理 1在忽略目标机动的影响,且弹目速度比ρ=‖VT‖/‖VM‖>1保持不变的情况下,末制导存在零控拦截条件:
γ=

(20)
证明(1)当η∈[0,π/2]时,拦截弹和目标形成碰撞三角形如图2所示。
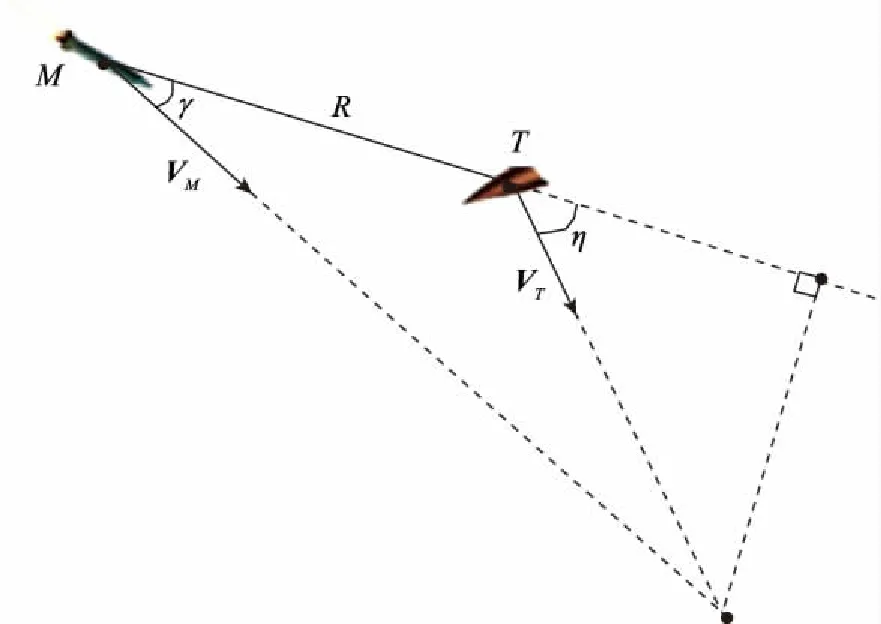
图2 碰撞三角形(情形1)
此时,根据几何关系可知拦截弹速度前置角γ需满足条件:
(21)
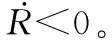
由图2可知γ<η,即sinγ
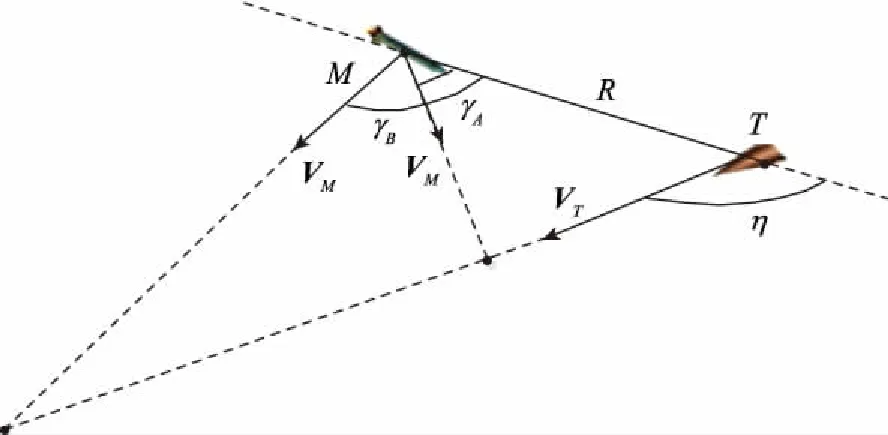
图3 碰撞三角形(情形2)
此时, 根据几何关系可知,γ需满足sinγ=ρsinη,η需满足0<ρsinη≤1,即η≥π-arcsin(1/ρ)。拦截弹有两种形式拦截目标,即γ=γA∈[0,π/2]或γ=γB∈[π/2,π]。
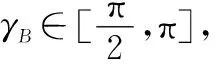
(22)
结合式(9)和式(22),得
(23)

综上分析可得,当π-arcsin(1/ρ)≤η≤π时,若γ=arc sin(ρsinη)或γ=π-arcsin(ρsinη),则拦截弹可实现零控拦截。
(3)当η∈[π,3π/2]时,证明过程同情形2,可以得出当π≤η≤π+arcsin(1/ρ)时,若γ=arcsin(ρsinη)或γ=-π-arcsin(ρsinη),则拦截弹可实现零控拦截。
(4)当η∈[3π/2,2π]时,证明过程同情形1,可得出,此情况下拦截弹无法实现零控拦截。
因此,若拦截弹状态满足式(20),则可在末制导中实现零控拦截,即定理1成立。
证毕
3.2 捕获区分析
定义 2滑模变结构制导律的捕获区定义在以拦截弹的速度前置角γ为横坐标轴,以目标的速度前置角η为纵坐标轴的(γ,η)平面内。当拦截弹对目标进行拦截时,在中末制导交接班终端时刻即末制导初始时刻,只要拦截弹速度前置角的初始值γ0和目标速度前置角的初始值η0组成的点(γ0,η0)处在捕获区内,拦截弹即可以滑模变结构制导律为末制导律对目标进行有效拦截。
将式(19)代入式(3)得
(24)
再将式(9)代入式(23)得
(25)
根据假设3,结合式(3)、式(4)和式(7)、式(8),得出以下关系:
(26)
将式(26)代入式(25)可以得出γ与η的对应关系:
(27)
定理 2在忽略目标机动的影响,且弹目速度比ρ=‖VT‖/‖VM‖>1保持不变的情况下,拦截弹末制导采取滑模变结构制导律时的捕获区在(γ,η)平面内可以表示为
CR=A∪B
(28)
式中:
A={(γ,η)|γ1≤γ≤γ+,T1(γ,η)≥0且f(γ,η)≤0}
(29)
B={(γ,η)|γ-≤γ≤γ2,f(γ,η)≥0且T2(γ,η)≤0}
(30)
T1(γ,η)=η-J(γ,η)+J(γ+,η)+η+
(31)
T2(γ,η)=η-J(γ,η)+J(γ-,η)+η-
(32)
(33)
其中γ+>0和γ-<0可利用以下方程组求解:
(34)
(35)
(36)
T1=(γ1,η1)=0,γ1=-π
(37)
T2=(γ2,η2)=0,γ2=π
(38)
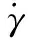
(39)
设初值γ(0)=γ0,η(0)=η0,式(39)两边对γ积分:
(40)
结合式(33),式(40)可简写为
η=J(γ,η)-J(γ0,η)+η0
(41)
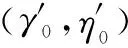
η*=J(γ*,η*)-J(γ0,η*)+η0
(42)
(43)
式(42)和式(43)相减得
(44)

图4 捕获区分析示意图
对于图2中的S1区域,其取值范围为
ρsinη>sinγ
(45)
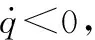
对于零控拦截条件式(20),两边对γ求导:
(46)
结合式(20),得
(47)
由式(33)和式(39)可知:
(48)
所以,γ+和γ-可利用方程组式(34)求解,进而η+和η-由式(35)和式(36)求解,得出交点(γ+,η+)和(γ-,η-)。
因此,滑模变结构制导律的捕获区为零控拦截曲线和两条与之相切,形如式(41)的曲线所构成的区域,如图4中的A∪B。
4 捕获区仿真分析
为验证本文对滑模变结构制导律捕获区分析的合理性,设计以下4种情形的仿真实验。这里选取制导律参数为k=20,ε=1,δ=0.01,导引头最大作用距离取Rmax=100 km,弹目初始条件如表1所示。

表1 弹目初始条件
根据定理2仿真出拦截弹最大可用过载分别为30和40的捕获区(A∪B)。
由图5可知,不同过载限制情况下,末制导的捕获区约束范围不同,且拦截弹最大可用过载越小,捕获区的范围也越小。另外,仿真所得捕获区的区域符合上文分析,为验证其正确性,以最大可用过载nmax=30为例,分别选取位于捕获区内的N点(100°,175°)和位于捕获区之外的M点(150°,190°)作为拦截弹与目标的速度前置角初始状态进行仿真。
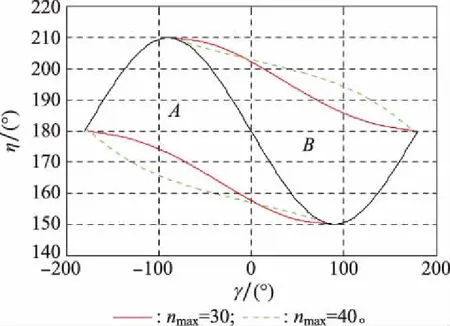
图5 捕获区范围
情形 1末制导采用滑模变结构制导律,点N(100°,175°)为拦截弹与目标的速度前置角初始状态,仿真结果如图6~图9所示。
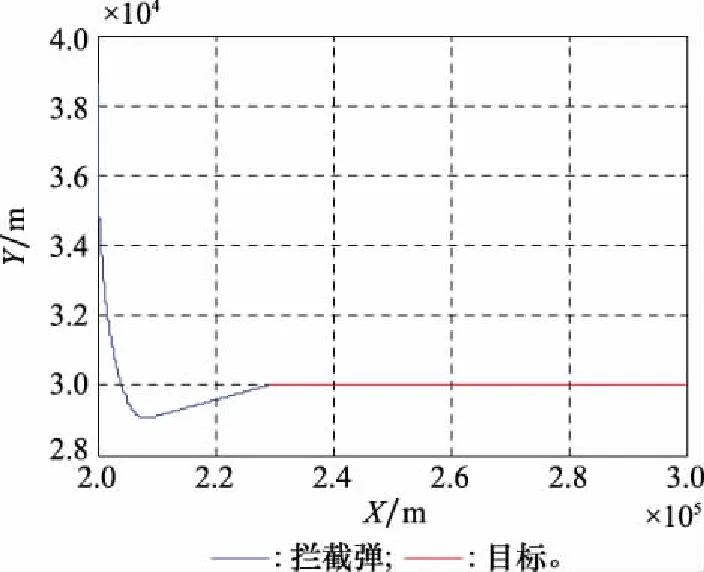
图6 弹目轨迹(情形1)
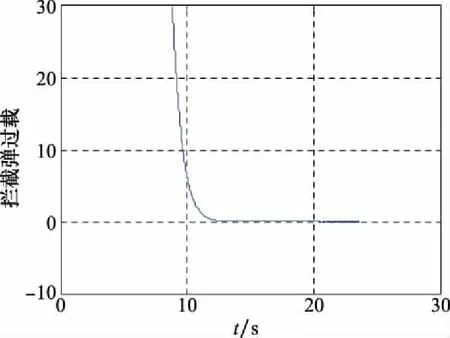
图7 拦截弹过载变化(情形1)

图8 视线角变化(情形1)

图9 捕获区曲线(情形1)
由图6可以看出,情形1中的拦截弹能够利用滑模变结构制导律成功拦截目标,且弹道末端平滑。由图7和图8可知,情形1中的拦截弹过载在末端收敛到零,视线角变化趋于稳定值,说明当拦截弹末制导初始状态处于捕获区内时,能够对目标形成有利拦截态势,从而成功拦截目标。由图9可知,拦截弹和目标的速度前置角关系在滑模变结构制导律的导引下,逐渐趋近于零控拦截曲线,证明了零控拦截条件的合理性。
情形 2末制导采用滑模变结构制导律,点M(150°,190°)为拦截弹与目标的速度前置角初始状态,仿真结果如图10~图13所示。

图10 弹目轨迹(情形2)
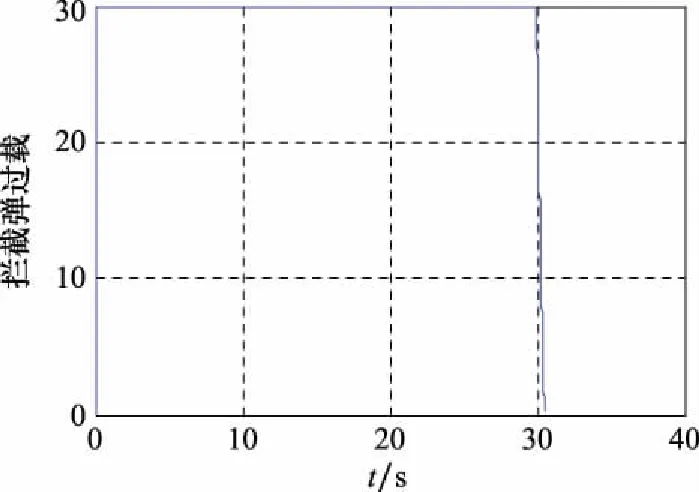
图11 拦截弹过载变化(情形2)
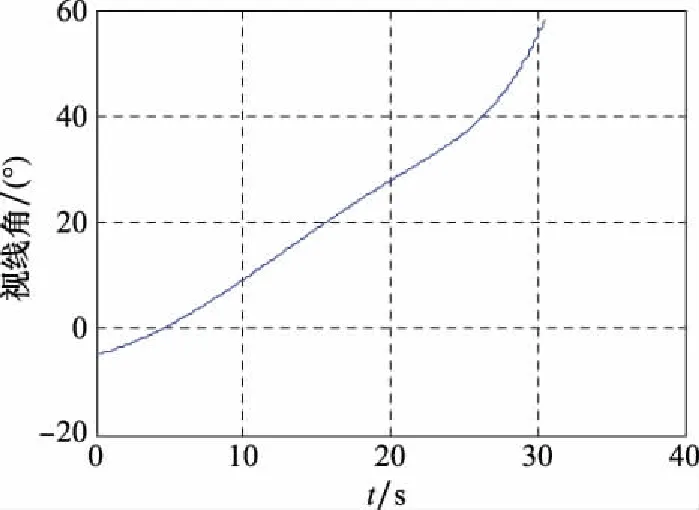
图12 视线角变化(情形2)
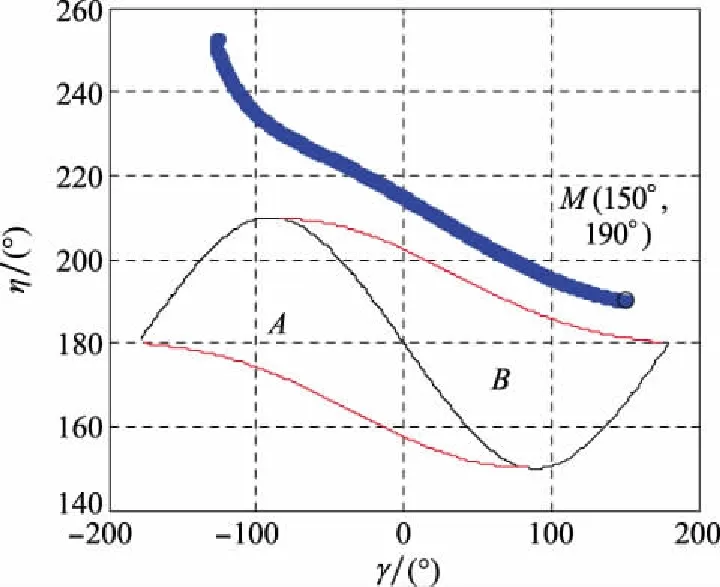
图13 捕获区曲线(情形2)
由图10可以看出,情形2中的拦截弹未能成功拦截目标。拦截弹的过载和视线角都在末端处于发散状态,如图11~图12所示。由图13可知,此时的拦截弹和目标的速度前置角关系未能在滑模变结构制导律的导引下接近零控拦截曲线。因为在之前的定理2中已推出了滑模变结构末制导律的捕获区范围,即拦截弹和目标的速度前置角初始值(γ0,η0)位于捕获区之内,在滑模变结构制导律的导引下,总能使得拦截弹和目标的速度前置角关系趋近于零控拦截曲线,拦截弹实现零控拦截。而在情形2中,拦截弹和目标的速度前置角初始状态不满足捕获区约束,拦截弹无法在末制导中通过滑模变结构制导律的导引命中目标,所以致使图10中弹目轨迹发散,对应的拦截弹过载和视线角变化呈现发散趋势。
情形 3末制导采用滑模变结构制导律,点N(100°,175°)为拦截弹与目标的速度前置角初始状态。此时假设目标做正弦机动,仿真结果如图14~图17所示。
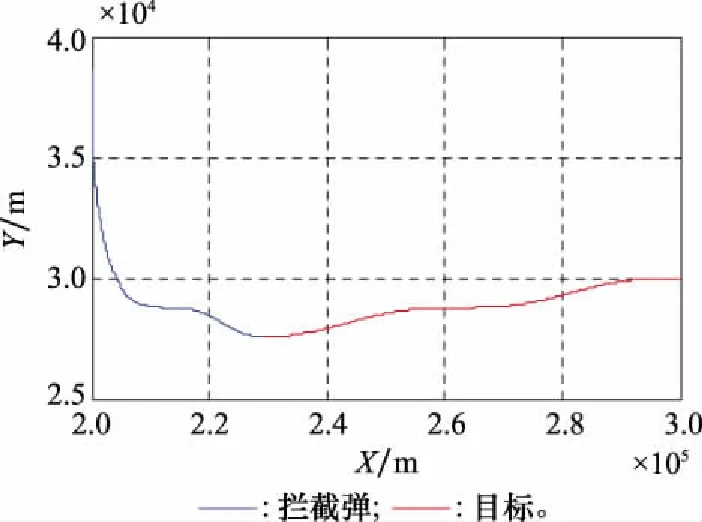
图14 弹目轨迹(情形3)
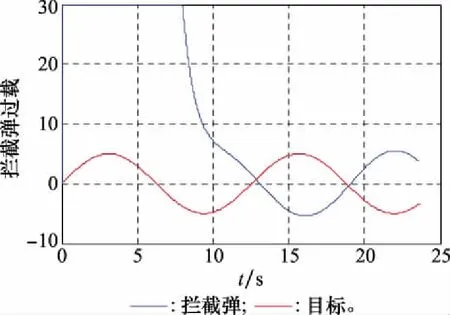
图15 拦截弹与目标过载变化(情形3)
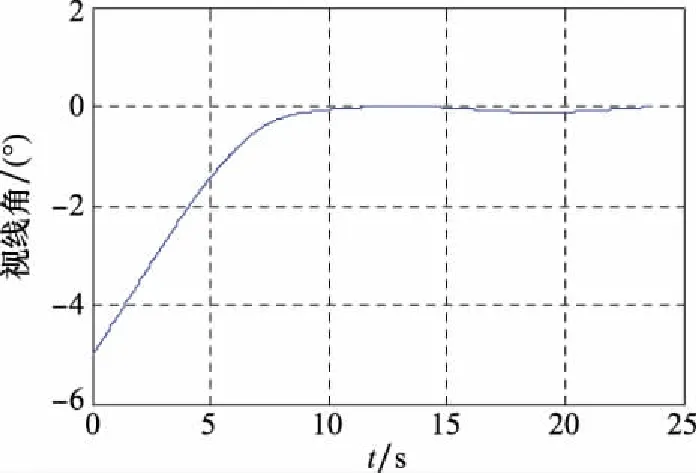
图16 视线角变化(情形3)
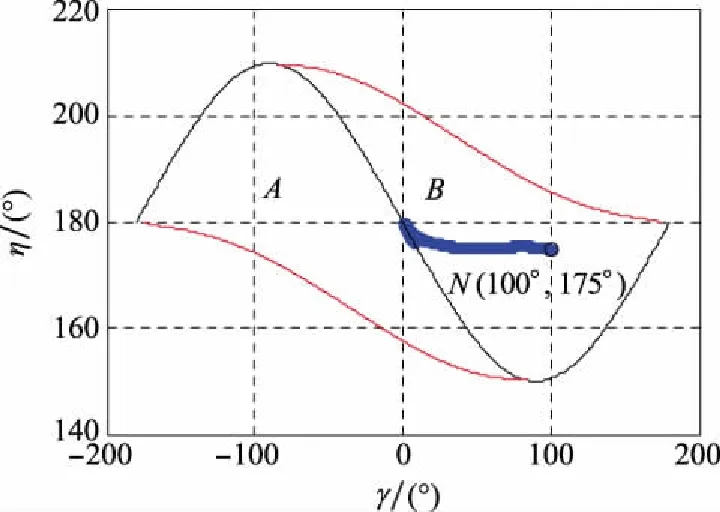
图17 捕获区曲线(情形3)
由图14~图17可知,拦截弹仍能成功拦截目标,拦截弹过载与视线角都在末端处于收敛状态,拦截弹和目标的速度前置角关系逐渐趋近于零控拦截曲线。结合情形1分析得出,当末制导拦截弹与目标的初始状态处于捕获区内时,目标机动对结果造成的影响相对较小,可以忽略,从而证明了本文方法的有效性。
情形 4末制导采用滑模变结构制导律,选取目标的速度前置角为η=180°,以5°为间隔,对拦截弹的速度前置角γ进行从-180°到180°的蒙特卡罗仿真实验,结果如图18~图20所示。
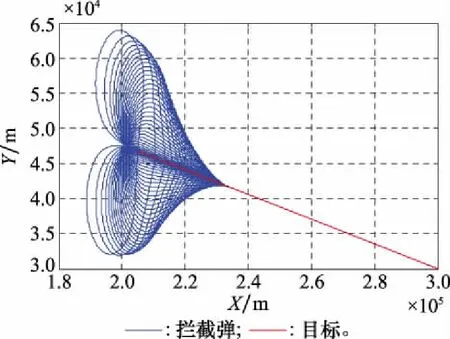
图18 弹目轨迹(情形4)
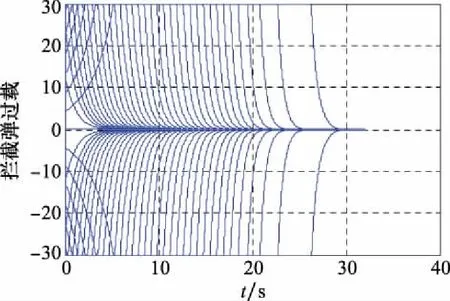
图19 拦截弹过载变化(情形4)

图20 捕获区曲线(情形4)
在情形4中,通过对蒙特卡罗仿真统计,可发现拦截成功时对应的拦截弹和目标速度前置角初始值(γ0,η0)均位于捕获区之内,且过载变化都趋于0。因此,结合结论可以得出,在拦截弹中制导修正阶段时,一定要确保其末端状态处于捕获区内,即捕获区是中制导终端状态的重要约束条件。
5 结 论
本文首先基于滑模变结构控制理论完成了滑模变结构制导律的设计,保证了拦截末端的过载收敛,并对其稳定性进行了证明,将捕获区的研究拓展到了现代制导律的领域。其次,分析了零控拦截条件,得出零控拦截状态下拦截弹与目标速度前置角的关系。然后,结合末制导弹目运动关系对滑模变结构制导律的捕获区进行了理论推导和分析。最后,通过4种情形下的仿真实验,验证了结论的正确性,为中末制导交接班的条件约束设定提供了理论支撑。
另外,本文研究针对的是目标不机动情况下的静态捕获区,下一步将研究结合目标机动影响的动态捕获区。
