杂波背景下机载雷达信号参数的射频隐身优化

于伟强, 汪 飞,*, 孙 萍, 周建江, 陈 军

(1.南京航空航天大学雷达成像与微波光子教育部重点实验室, 江苏 南京 211106;2.南京信息工程大学电子与信息工程学院, 江苏 南京 210044)

0 引 言

机载雷达采用下视工作模式探测地面或海面目标时,会根据目标的多普勒特点采用不同的目标检测算法,其中目标回波中的杂波是干扰机载雷达目标探测性能最重要的因素。

针对运动速度较快的面目标,脉冲对消是被广泛应用的技术,该方法具有实时性强的特点。为了提高动目标检测的效率,Hassanieh等人提出了基于稀疏傅里叶变换(sparse Fourier transform,SFT)的检测算法,该算法虽然具有较高的动目标检测效率,但是需要预先设定信号的稀疏性[1]。Zuo利用目标与背景之间存在的多普勒特征不一致特性,对采样数据的时频分解进行重构,通过迭代获取最接近原采样数据的时频分布图,从而提取目标[2]。为了利用目标可能具备的多维微多普勒特性,Chen利用短时多维分数阶傅里叶变换分析了目标与海杂波的多维微多普勒特征,有效地从尖锐型海杂波中提取了目标[3]。Wang等人将SFT算法扩展到高维空间,利用目标的多维速度分量提升了SFT算法的性能,称之为鲁棒的SFT(robust SFT,RSFT)检测算法[4]。Yu针对复杂的杂波场景,提出先利用比例恒虚警(constant false alarm rate，CFAR)检测算法对杂波类型进行分区,再对各类杂波区采用对应的RSFT算法字典检测动目标,以进一步提高算法的实际应用效率[5]。Chen分析了RSFT的特点,指出RSFT算法的本质是通过搜索匹配信号提高信杂比,对信号特性具有一定的依赖性,然后从抑制杂波而非搜索匹配信号角度提出了较普适的自适应稀疏分数阶模糊函数(adpative sparse fractional ambiguity function,ASFRAF)方法[6]。

针对运动速度慢或者静止的面目标,除了采用成像的方法提取目标以外,CFAR算法是机载雷达提取慢速目标或静止目标的主要方法。Meng针对韦布尔分布,分析了各种CFAR的目标提取性能,给出了顺序统计量CFAR具有最优目标提取效果的结论[7]。Xu将模糊理论应用于CFAR,针对K分布,设计了一种基于模糊判别的CFAR算法,仿真表明这种模糊检测对防止长期丢失小目标信号是有效的[8]。Tao考虑到有限采样数据的统计分布与假设分布之间的不一致会影响到CFAR的检测效果,提出先基于有限采样数据估计统计分布,再选择相应的CFAR算法,提高了CFAR算法的稳健性[9]。Zhou针对海杂波数据的幅度起伏特点,设计了基于幅度加权迭代的修正CFAR检测算法,提高了CFAR算法的稳健性[10]。Yang利用正交投影技术,先对采样数据进行高维正交投影分解,再对存在奇异值的投影维度进行CFAR检测,从而提取目标信息[11]。Zhang针对海杂波难以用固定的对数分布、韦布尔分布或K分布描述的情形,提出混合多种分布的CFAR算法,通过数据采样输入与CFAR输出之间的交互自适应地选择适合当前分布的CFAR算法[12]。Dai提出先利用采样数据的累积分布函数估计当前的杂波概率分布函数,再根据估计的概率分布函数选择适用的CFAR算法提取目标[13]。

近年来,人们除了进行检测器设计与CFAR设计以外,还从波形设计、空间分集、极化分集等角度深入挖掘机载雷达探测面目标的潜力[14-16]。但是,已有的这些研究都未考虑机载雷达在探测面目标时的射频隐身性能。随着武器研究的发展,飞行器所要面临的威胁不仅来自敌方主动雷达,还将来自敌方的无源探测系统。无源探测系统不同于主动雷达,其并不对外辐射信号,只被动接收敌方主动雷达发射的信号,因此具有隐蔽性。除了飞行器雷达隐身、红外隐身以外,为了避免机载雷达探测目标时的主动辐射信号被敌方无源探测系统截获,保证打击任务的有效实施,需要机载雷达在战场上采用射频隐身技术[17-18]。当前对射频隐身技术的研究主要集中在低截获波形设计[19-20]和雷达辐射能量控制[21-22]两方面,而缺乏对杂波背景下机载雷达多参数控制及优化的深入探讨。

本文将飞行器的射频隐身需求引入机载雷达探测地面或海面目标时的工作模式中。分别基于脉冲对消滤波和CFAR检测技术,研究了杂波背景下机载雷达的探测性能和射频隐身性能,建立了以最小化截获因子为优化目标,以驻留时间、探测距离、信杂比为约束的射频隐身信号参数优化模型,并基于该模型分析了目标散射截面积、地杂波与海杂波散射系数对机载雷达射频隐身性能的影响。

1 杂波背景的信号参数射频隐身优化

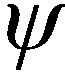
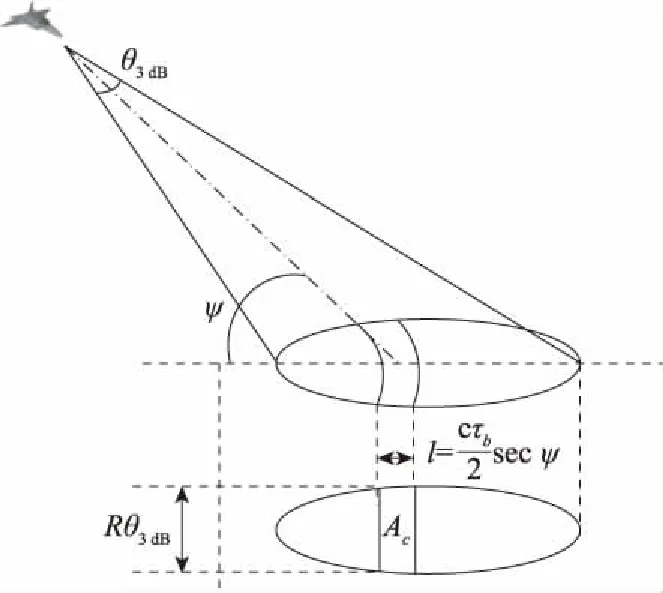
图1 雷达下视模式的辐射区

则地面杂波的雷达散射截面(radar cross section, RCS)[23]可近似表示为

(1)

式中：τb为脉压后的脉冲宽度；R为雷达与照射区的距离；c代表光速；σ0为杂波散射系数。因为雷达接收的杂波相当于雷达照射到RCS大小为σc的物体上的回波,所以雷达接收机端的信杂比可以表示为目标的RCS值σt与杂波RCS值σc的比值[23],定义为

(2)

为了抑制杂波干扰,回波信杂比SCRR需要大于预设的门限值SCRth,雷达对当前区域的扫描时间Td要小于雷达的最大驻留时间Td max。为了避免雷达盲速且确保脉冲雷达探测距离的唯一性,雷达信号的脉冲重复周期Tp的选取准则为

(3)

式中：RD代表雷达对目标的探测距离;λ代表雷达信号波长;v代表目标相对于雷达的径向速度。

为了定量分析雷达的射频隐身性能,施里海尔提出了截获因子[24]。其被定义为确定检测概率与虚警概率条件下,对方无源探测系统对我方雷达信号的最大截获距离RImax和我方雷达的最大探测距离RD max之比,截获因子α定义为

αRImax/RD max

(4)

式中：

(5)

(6)

式中：PT代表雷达辐射功率;τ代表雷达信号脉压前的脉冲宽度;GI为截获接收机的信号处理增益;k0代表玻尔兹曼常数;T0代表噪声温度;N为脉冲积累个数,η代表脉冲积累效率;GT和GTI分别代表雷达指向目标与截获接收机的天线增益,当目标与截获接收机在同一个距离单元内时,GT=GTI;LR和LI分别代表雷达与截获接收机的信号处理损耗;BI代表截获接收机的信号处理带宽;FR和FI分别代表雷达与截获接收机的噪声系数;SNRR min和SNRImin分别代表雷达与截获接收机的最小检测信噪比。

截获因子越小,越有利于机载雷达改善其射频隐身性能。若要求雷达的最小探测距离为RD min,则杂波条件下脉冲雷达射频隐身求解模型可以描述为

(7)

接下来分别在地杂波、海杂波条件下针对脉冲体制雷达对该模型作进一步推导与分析。

1.1 地面动目标的脉冲对消检测模型

当目标存在相对运动时,可以利用目标的多普勒信息进行目标检测,以改善式(2)的信杂比,实现目标的探测。基于脉冲对消的地面动目标检测利用脉冲多普勒技术提取目标的运动速度参数。脉冲对消滤波器采用延迟对消的方法,其通用的滤波器结构如图2所示。若参与对消的脉冲个数为n,则将其称为n-1次脉冲对消滤波器。

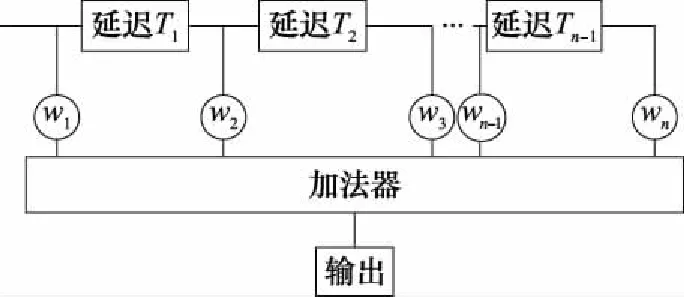
图2 脉冲对消滤波器结构

其中,wk为图2中第k个滤波器抽头的系数,对于n-1次脉冲对消滤波器,wk[25]可以表示为

(8)

通常用改善因子Ic表示多普勒滤波对信杂比的提升程度。脉冲对消不能改善噪声,所以当脉冲对消改善因子很大时,检测器的性能趋于噪声限制的情况,当杂波的功率谱宽度较窄时(2πσfTp→0),改善因子[25]可以表示为

(9)

式中：σf为杂波功率谱的标准差；Tp为脉冲重复周期。对于二阶脉冲对消滤波器,参与对消的脉冲数n=3,则Ic可以表示为

(10)

图3给出了原始回波经过一、二、三阶脉冲对消处理后的结果以及各阶脉冲对消改善因子对比曲线,其中,PRF为脉冲重复频率。

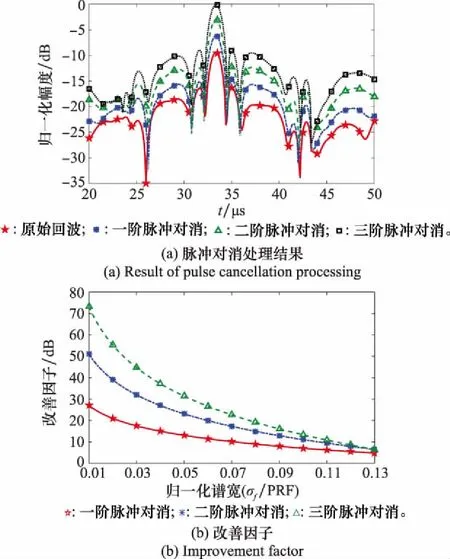
图3 各阶脉冲对消处理结果与改善因子

显然,在经过脉冲对消处理后,目标回波的幅值明显增大,并且三阶脉冲对消比一、二阶脉冲对消具有更好的改善因子。

图4为一、二、三阶脉冲对消滤波器的归一化幅频响应,其中,f为多普勒频率。由图4可知,脉冲对消滤波器对多普勒频移近似为0的地杂波有较好的抑制效果。随着对消器个数的增加,脉冲对消滤波器的通带会变窄,在杂波功率谱一定的情况下,较窄的通道虽然可以明显提高杂波的改善因子,但也可能使目标信号被滤除。

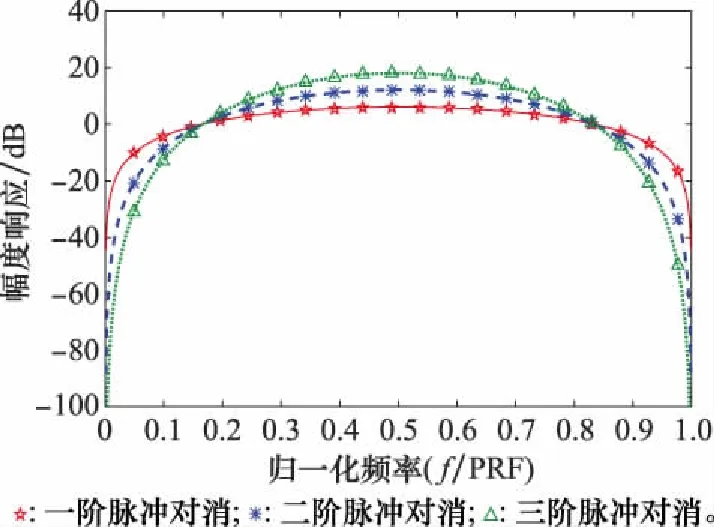
图4 归一化幅频响应

通常情况下,一般会采用在滤除杂波和保留目标信息这两点上都具有较好表现的二阶脉冲对消滤波器。

1.2 基于射频隐身的地面动目标检测

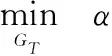
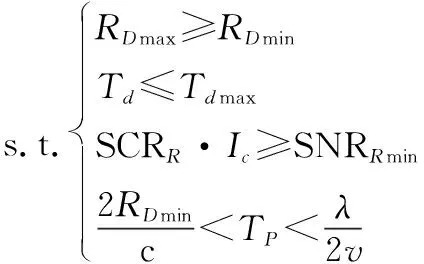
(11)

根据式(5)和式(6)将目标函数中的RImax和RD max取对数展开,可表示为

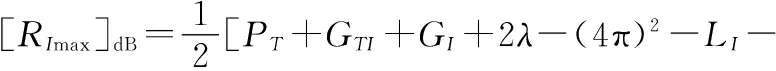
k0-T0-BI-FI-SNRImin]dB

(12)

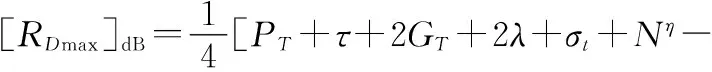
(4π)3-LR-k0-T0-FR-SNRR min]dB

(13)

式中：[·]dB代表对变量取对数。则当GT=GTI时,舍弃截获因子α中非优化参数后的对数,表示为

(14)

将式(13)中的非优化参数定义为Kc1,则雷达探测距离的约束为

[PT+τ+2GT+Nη+Kc1]dB≥[RD min]dB

(15)

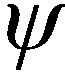
(16)

式(16)中隐含的限制条件是脉冲重复周期Tp越大,σf就要越小;机载雷达照射目标的夹角确定后,机载雷达离目标越远,雷达波束覆盖的区域越大,信杂比就越低。式(11)中驻留时间Td与单个波束位置上最大脉冲发射个数N和波束宽度θ3 dB有关,可表示为

(17)

式中：Δθ为雷达空域的扫描范围,对于相控阵体制的雷达,考虑其阵列天线在法线方向±45°工作角度,则Δθ=90°。

1.2.3 手术成功标准 采用介入封堵方法治疗后并未出现需转外科术式等并发症，外科手术治疗后未发生死亡。

根据经验公式GT=29 000/(θeθa),其中,θe与θa分别代表天线在俯仰与方位向上的3 dB增益。则可以用GT表示θ3dB。根据以上分析,式(11)的模型可变化为

(18)

式中：Kc3代表式(11)中驻留时间约束项的非优化参数。式(18)即为地面动目标检测的雷达射频隐身工作参数优化目标模型。

1.3 基于射频隐身的海面目标检测

海杂波功率谱的平均多普勒频移通常不为0,目标与杂波在多普勒频谱上容易混叠,因此适用于地杂波的脉冲对消滤波对海杂波的抑制效果较差,通常会出现较多的虚警。针对海面目标检测,这里基于典型的单位平均CFAR(cell-averaging CFAR,CA-CFAR)对式(7)进行分析推导,以得出海杂波背景下雷达信号参数的射频隐身优化模型。

当回波信号中的杂波为均匀高斯分布时,CA-CFAR检测器的检测概率Pd可由式(19)计算,虚警概率Pfa可由信杂比SCRR为0时的检测概率得到[26]:

(19)

式中：m为检测单元一侧的参考单元长度；K为标准化因子。综合式(7)与式(19),则海杂波背景下机载雷达的射频隐身参数优化模型可表示为

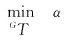
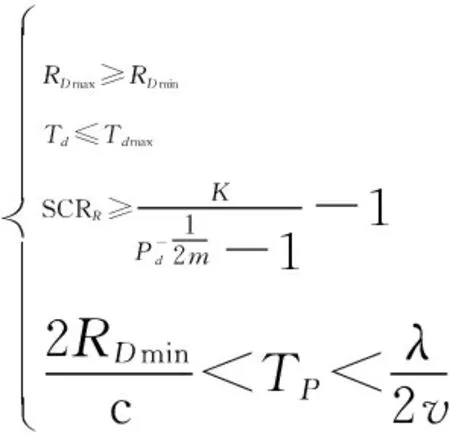
(20)

相比于地杂波下的射频隐身模型,两者都采用脉冲体制的雷达,不同的地方在于两者面对的杂波不同,并且处理方法不同,则除了SCRR的约束外,其他约束都相同。将SCRR按照式(2)展开,将非优化参数定义为Kc4,联合式(18),则式(20)可重新表示为

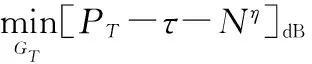
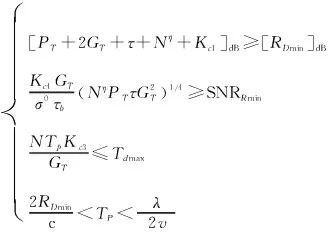
(21)

式(18)与式(21)分别针对的是地杂波与海杂波背景下的机载雷达信号参数优化模型,具有以下共同特点:

(1)从目标函数上看,若GT确定,则PT越小,τ与N越大越好;

(2)约束条件[PT+2GT+τ+Nη+Kc1]dB≥[RD min]dB与PTτN呈正相关;

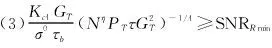
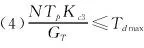
综上分析,式(18)与式(21)有解但不一定存在唯一解。特别是当脉冲积累因子η变化时,式(18)与式(21)的解会存在更多变化。不失一般性,仿真中设η=1并采用成熟的遗传算法对式(18)与式(21)的参数寻优求解。

2 数值仿真分析

本节分别对地杂波、海杂波条件下构建的脉冲雷达参数的射频隐身优化模型进行求解和分析。表1给出了这些参数的优化取值区间。

表1 脉冲雷达的参数取值范围

采用遗传算法对式(18)与式(21)的参数PT、τ、N、GT和τb进行优化求解时，分别将两式的目标函数值作为适应度，同时优化参数按二进制编码，设置交叉概率为0.6，变异概率为0.001，初始种群个体数为200个，选择遗传50 000代之后样本中的最佳适应度个体各参数的值分析模型的射频隐身性能。

2.1 地杂波下雷达信号参数设计模型的求解与分析

表2给出了地杂波下的射频隐身模型中一些非优化参数的取值区间。

表2 对地目标探测的参数取值范围

若取地杂波散射系数σ0=-25 dB，目标RCSσt=5 m2，最小探测距离RD min=41 km，最大驻留时间Td max=1 s，则最终从样本中选择的最佳个体适应度为0.37，即目标函数的最优值为0.37，目标函数值小于1表明雷达具备实现射频隐身的条件，最佳个体的PT=9.91 dBw、τ=73.10 μs、N=998、GT=34.64 dB、τb=0.08 μs。采用此参数的雷达对不同距离处的目标的探测概率和被同样远的无源截获的概率如图5所示，当距离小于20 km时，雷达和无源相互之间都能发现对方，距离大于20 km之后，雷达对无源的探测概率显然高于无源对雷达的截获概率，并且在60 km处雷达的发现概率为0.98，而无源的截获概率只有0.005，雷达具有较好的射频隐身性能。

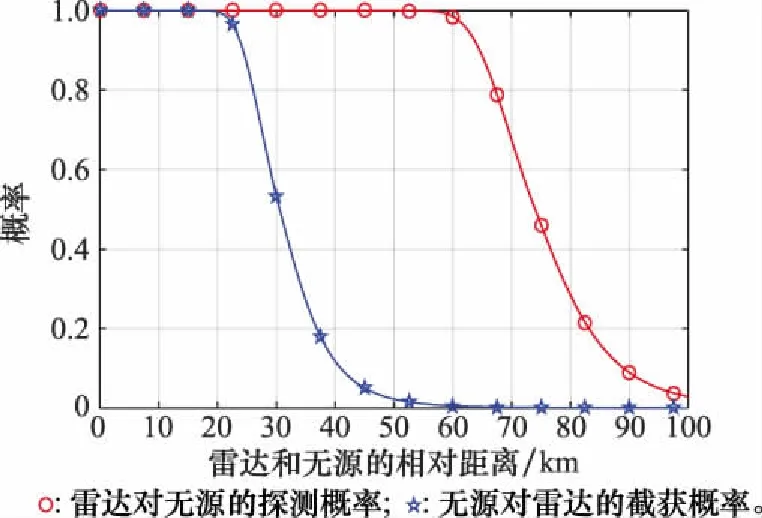
图5 地杂波下雷达和无源相互间的发现概率

设散射系数σ0=-25 dB，面对不同RCS大小的目标，当雷达的最小探测距离RD min变化时，求解模型得出的最佳个体对应的截获因子的变化如图6所示(当RCS为0.3 m2并且RD min大于130 km时，截获因子趋于无穷大，在图6中未画出)。由图6可知，目标RCS小于0.3 m2时不存在具有射频隐身能力的雷达参数，由截获因子随RD min的增大而增大，随RCS的增大而减小，我们可推知目标RCS大于0.3 m2时，RD min在某一范围内雷达具备射频隐身性能，并且当RCS的范围为7～50 m2时，RD min最小探测距离在150 km以内，都存在满足射频隐身条件的雷达信号参数。

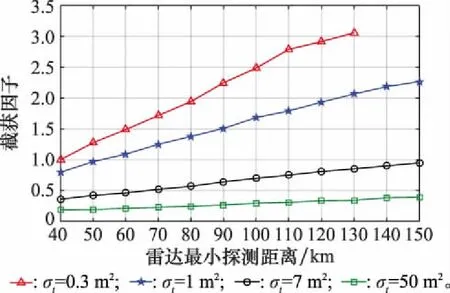
图6 地杂波下目标RCS与截获因子的关系

设目标RCS的大小为5 m2，面对不同的地杂波散射系数σ0，当雷达的最小探测距离RD min变化时，求解模型得出的最佳个体对应的截获因子的变化如图7所示。由图7可知，当杂波散射系数在-31～-16 dB变化时，最佳个体对应的截获因子的变化很小，并且最小探测距离在130 km以内雷达都具有射频隐身性能，当探测距离超过140 km时，将无法获得具有射频隐身能力的雷达信号参数。

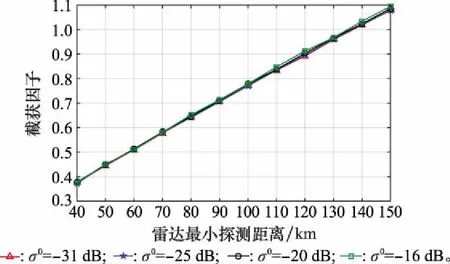
图7 地杂波下杂波散射系数与截获因子的关系

2.2 海杂波下雷达信号参数设计模型的求解与分析

表3给出了海杂波下的射频隐身模型中一些非优化参数的取值区间。

表3 对海目标探测的参数取值范围

若取海杂波散射系数σ0=-30 dB，目标RCSσt=1 000 m2，最小探测距离RD min=41 km，最大驻留时间Td min=1 s，则最终从样本中选择的最佳个体适应度为0.087 5，即目标函数的最优值为0.087 5。最佳个体的PT=6.90 dBw、τ=73.19 μs、N=646、GT=32.31 dB，τb=0.01 μs。采用此参数的雷达对目标的探测概率和被无源截获的概率如图8所示，当距离小于10 km时，雷达和无源相互之间都能发现对方，距离大于10 km之后，雷达对无源的探测概率显然高于无源对雷达的截获概率，并且雷达对相距40～100 km处目标的发现概率为1，此时无源对雷达的截获概率为0，雷达具有较好的射频隐身性能。

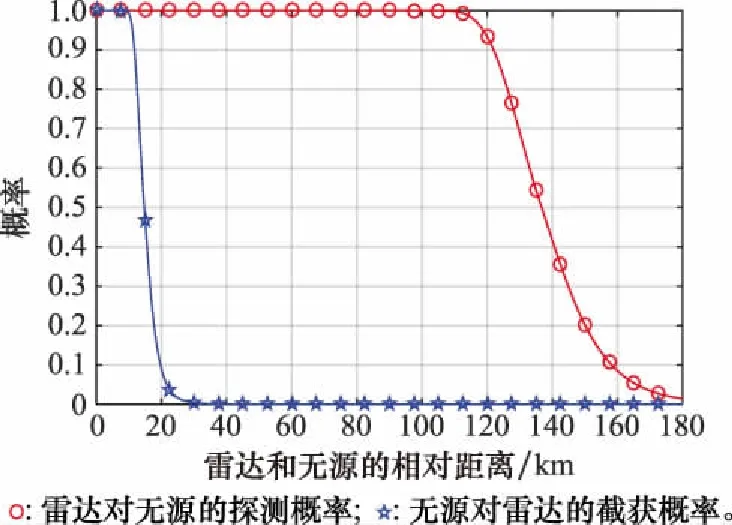
图8 海杂波下雷达和无源相互间的发现概率

设散射系数σ0=-30 dB,面对不同RCS的目标时,当雷达的最小探测距离RD min变化时,求解模型得出的最佳个体对应的截获因子的变化如图9所示。由图9可知,RCS越大的目标,越容易获得射频隐身性能,并且最小探测距离越大,射频隐身性能越低。在40～180 km范围内,目标RCS大于等于1 000 m2的情况下,都存在满足射频隐身条件的雷达信号参数。

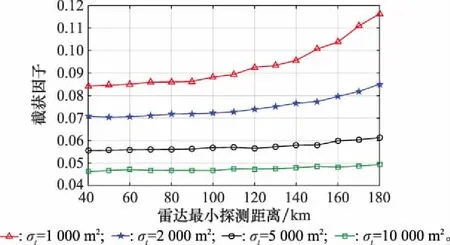
图9 海杂波下目标RCS与截获因子的关系

设目标RCS的大小为1 000 m2,在不同的海杂波散射系数下,当雷达的最小探测距离RD min变化时,求解模型得出的最佳个体适应度的变化情况如图10所示。由图10可知,杂波散射系数越小,雷达的射频隐身性能越好,当杂波散射系数在-35～-30 dB范围内变化时,最佳个体对应的截获因子基本不变。此外,当雷达的最小探测距离在40～180 km范围内,杂波散射系数小于等于-22 dB的情况下,都存在满足射频隐身条件的雷达信号数。

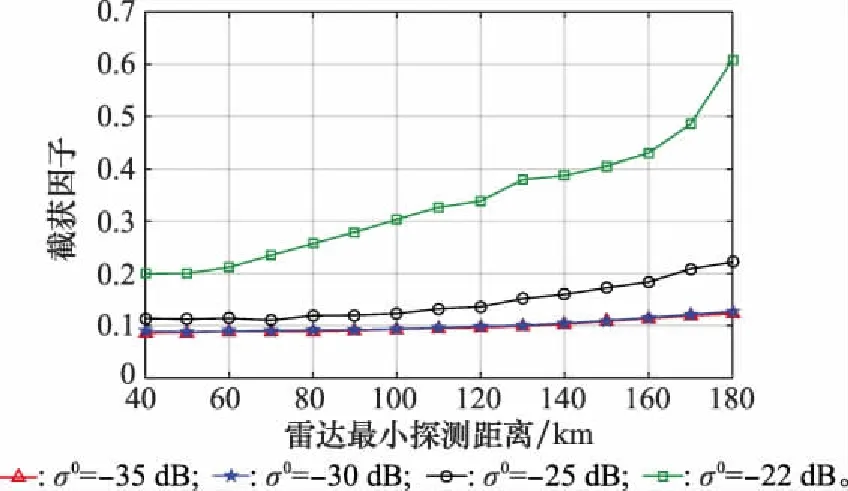
图10 海杂波下杂波散射系数与截获因子的关系

3 结 论

目前,杂波背景下机载雷达信号的射频隐身优化国内外尚未有公开报道。本文针对杂波背景推导分析了机载雷达信号参数的射频隐身优化模型,并分别将其应用于地杂波与海杂波背景,给出了分别适用于地杂波与海杂波背景的机载雷达信号参数的射频隐身优化模型。数值仿真实验给出了机载雷达信号参数优化后的射频隐身性能,分析了机载雷达信号在杂波背景下具备射频隐身性能的条件。杂波背景的机载雷达信号参数优化受到许多因素影响,例如地杂波中草丛的多普勒展宽,海杂波中海情变化,这些都需要在以后进行更深入的分析与研究。