大规模图推荐模型的快速优化机制

杨正一, 吴 宾, 王 翔, 何向南,4

1 中国科学技术大学 信息科学技术学院 合肥 中国 230026

2 郑州大学 信息工程学院 郑州 中国 450001

3 新加坡国立大学 NExT++中心 新加坡 新加坡119077

4 中国科学技术大学 大数据学院 合肥 中国 230026

1 引言

这是一个推荐系统无处不在的时代。随着数字化的大力推进和大数据的迅猛发展, “信息过载”成为了当今不得不面对的问题。面对海量的数据, 用户迫切需要高效的推荐系统帮助他们快速获得感兴趣的信息。对推荐系统需求的涌现推动了学术界和工业界对其投入了大量的研究。

推荐系统中, 用户-物品交互图是研究的根本。这是天然存在于推荐系统中的二分图, 其中用户和物品作为图的结点, 交互行为作为图的边。推荐系统的基本任务就是从用户和物品的历史交互中学习用户的偏好和物品的特性。经典的基于交互图的推荐模型有矩阵分解(matrix factorization, MF)[1]等, 自此初步开始利用图来建模用户物品交互。近些年来。深度学习迎来了日新月异的发展, 研究者们将深度学习的方法应用于推荐系统中, 取得了令人瞩目的效果。在文献[2]中, 作者用多层感知机取代传统的内积来模拟用户和物品的交互; 文献[3]更是将注意力机制引入推荐系统。近来图卷积网络(graph convolution network, GCN)在图分类和结点辨识等任务上取得了重大突破[4-5], 吸引了许多学者的注意, 推荐系统中交互图的存在, 使得图卷积网络在推荐任务上大有作为。许多基于图卷积网络的推荐模型如neural graph collaborative filtering(NGCF)[6], LightGCN[7]等,应用图卷积操作在交互图上传递用户和物品特征, 大大提高了推荐的准确性。越来越多的研究表明, 相比于传统的推荐模型来说, 基于深度学习的推荐模型能取得更好表现。

推荐系统模型设计完成之后, 需要进一步优化以取得优异的表现, 此时需要损失函数来重建用户和物品的历史交互记录, 进而学习模型的参数。在推荐系统中, 广泛使用的是贝叶斯个性化排序(Bayesian personalized ranking, BPR)损失函数[8], 其思想是通过最大化已观测交互与未观测交互之间的评分差来优化模型, 现已在研究和应用中都取得了优异的效果。但其在数十年之前机器学习尚未流行的时代已经提出, 需要人工计算损失函数的梯度来学习模型参数。而当前业界更多是在能够自动微分的深度学习平台如TensorFlow、Pytorch 上进行模型的自动优化, 并且一般采用批量梯度下降的方法,从而充分利用GPU 的并行计算实现优化操作, 这些是BPR 设计之初没有考虑的。现有的大多数研究都集中于将深度学习应用在推荐系统的模型设计上,然而随着模型设计的日渐复杂, 却几乎没有工作探索现有优化框架的不足, 更未曾提出新的解决办法。

本文的重点放在了模型训练的优化框架上, 尤其是GPU 上基于图推荐模型的学习。我们分析了BPR 在GPU 上训练效率低下的原因。BPR 的基本流程是对于一个用户, 从其交互过的物品中采样一个作为正样本, 从其未交互过的物品中采样一个作为负样本, 由此形成一个正负样本对, 然后最大化正样本评分高于负样本评分的概率。为了简单验证BPR 无法充分利用GPU 的性能, 我们使用BPR 训练矩阵分解模型MF: 在Amazon-book 数据集上, 设置相同的模型超参, 在CPU(i9 9000kf)上进行一次迭代仅耗时1.1 s, 而在GPU(2080Ti)上进行一次迭代需要55 s。可以明显看出, 模型在GPU 上进行一次迭代花费了更多的时间, 其原因在于BPR 计算无法充分利用GPU 的并行计算。更准确的来说, 对于每一个正负样本对, BPR 都需要计算它们的评分差, 然后单独通过非线性激活函数比如sigmoid, 这种对多个样本损失函数求和的计算方式, 无法转化成向量或者矩阵运算的形式。而GPU 的加速性能本就来自大量的向量和矩阵运算, 缺乏这些运算使得BPR 难以利用GPU 来提升训练效率, 这也成为了制约推荐模型在大规模实际场景中应用的瓶颈, 第3 节将对此进行更深入的实验分析。尽我们所知, 虽然以往的工作提及了BPR 效率低下[9], 但本文首次深入分析了BPR在GPU 上得到效率难以提升的原因。

在研究了BPR 不能充分利用GPU并行计算性能之后, 本工作致力于为推荐系统寻找更高效的优化方法。在对平方误差损失函数进行深入分析后, 我们提出了一种快速且通用的学习方法FGL(fast and generic learner), 其计算在推荐系统的假设之下包含两部分: 第一部分是只包含正样本的元素级别的计算, 计算复杂度较低; 第二部分包含所有的用户-物品对, 计算复杂度较高, 但通过线性代数的知识, 可以将其完全转化为矩阵运算的形式, 在理论上降低计算复杂度, 并能充分利用GPU 对矩阵运算的加速性能。除了加速优化过程外, FGL 会用到所有的负样本, 因此相比于BPR 节省了负采样时间。利用所有负样本还能够更充分地从负样本中提取有用信息,因而在负样本比例较大, 即数据集稀疏的情况下,FGL 将取得更好的性能, 实验中也验证了这一假设。在实际场景中, 推荐系统的数据集往往是非常稀疏的, 因此FGL 可以在工业界发挥巨大潜力。

本文挑选矩阵分解MF[1]和LightGCN[7]作为经典的图推荐模型和基于图卷积网络推荐模型的代表,并将FGL 应用其中。大量的实验结果表明在使用GPU 进行训练时, 新的优化框架FGL 相比于BPR 而言能够带来数量级层面上的效率提升, 并且在较稠密数据集上准确性表现与BPR 不相上下, 在较稀疏数据集上会比BPR 取得更好的推荐结果。本文所用到的的数据集和代码公布在: https://github.com/YangZhengyi98/FGL。

本文的主要贡献如下:

(1) 我们首次深入分析了推荐系统中主流的优化框架BPR 在利用GPU 进行训练时效率低下的原因。

(2) 我们在推荐系统的框架下改进了平方误差损失函数, 并通过代数学知识将其转化为计算复杂度更低的矩阵运算的形式, 并提出我们的优化框架FGL, 大大提高了GPU 的利用率。

(3) 我们通过大量的实验验证了FGL 的准确性和高效性, 并初步为其寻找了合适的应用场景。

2 推荐系统简介

我们关注基于协同过滤(collaborative filtering)[10]的推荐系统。协同过滤假设有过相似行为的用户会喜欢相似的物品, 因此可以从用户和物品的历史交互记录中捕捉用户的兴趣。我们用I 表示所有物品的集合, U 表示所有用户的集合。 O+表示所有观测到的用户-物品交互的集合(即正样本), 其中( u , i , yui)∊O+表示用户u 对物品i 的评价分数为 yui。一个推荐系统模型可以抽象表示为一个函数f :U × I →R , 即给定一个用户-物品对( u , i ), 推荐系统会输出一个分数yˆui, 表示模型预测的用户u 对物品i 的感兴趣程度, yˆui越大表示系统推测用户u越有可能选择物品i。推荐模型f 通常用一系列参数进行建模, 一般来说我们将一个用户u 对应到一个用户向量 eu, 将一个物品i 对应到一个同维度的物品向量 ei, 并通过用户向量和物品向量来重建用户和物品间的历史交互记录。MF 模型中用户向量和物品向量通过随机初始化得到, LightGCN 模型中通过图卷积网络得到。

在深度学习尚未开始流行的时代, 推荐系统早期的研究包含了若干具有自己特色的观点: (1)数据方面。不同于显式反馈, 即用户对物品的喜好程度以评分的形式呈现, 更多的数据是隐式反馈[11]: 我们认为用户的不同行为都能体现用户的兴趣, 比如说点击、评论、购买、浏览等, 因此用户对物品的兴趣不再以高低不同的评分表示, 而是分为了感兴趣(正样本)和不感兴趣(负样本)两类。正样本从历史交互记录中很容易得到, 负样本在的获得在推荐系统中一般基于如下假设: 一个用户没有交互过的物品,都认为用户对其不感兴趣。(2)损失函数方面。基于数据的正负样本, 两种类型的损失函数都被大量使用: 单点(point-wise)损失函数[11-12]通常遵循回归框架, 即最小化预测值与真实值之间的距离; 配对(pair-wise)损失函数[8,13]的观点是正样本的评分应该高于负样本, 因而要最大化它们的评分差。(3)优化方面。模型参数的学习通过对损失函数的优化来实现,经典的做法是先人工计算出损失函数的梯度, 再用梯度下降法对其优化。上述观点都是在数十年前提出的, 当时机器学习和深度学习尚未兴起, 在CPU上进行实验还是主流。如今学术界和工业界的实验都通过 GPU 在深度学习平台如 TensorFlow 和Pytorch 上进行, 因此直接将其搬移过来并不合适。

3 BPR 效率分析

3.1 BPR 公式

BPR(Bayesian personalized ranking)是推荐系统中基于隐式反馈的配对(pair-wise)损失函数的代表。其核心思想是对于一个用户的一个正样本, 随机取样一个负样本, 组成一个训练对, 然后最大化正样本与负样本预测评分的差值。在GPU 常用的分批训练(mini-batch training)策略中, 如公式(1)所示:

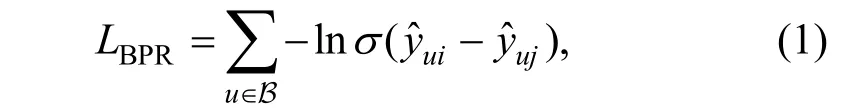
其中, B 表示一批训练的用户, 其中每个用户都从O+={(u , i, yui)}中采样一个感兴趣物品i , 再从O-= U ×IO+中采样一个不感兴趣的物品j ;σ (∙)表示sigmoid 函数。遵循主流方法, 用户u 对物品i 的预测分数用对应用户向量和物品向量的内积表示, 即:

通常会用SGD[14]或者Adam[15]作为优化器来进行梯度反向传播, 从而更新模型的参数。

3.2 原因分析

然而, 实验中发现在GPU 上采用分批训练的策略时, 用BPR 作为损失函数来训练模型会耗费大量的时间, 尤其是随着深度学习方法在推荐系统中得到广泛应用, 推荐模型逐渐复杂, 更使得训练模型的效率十分低下。我们认为这种低效性源于BPR 的负采样策略和BPR 损失函数的公式: (1)在一个训练批次中, 对于每一个用户, 都要对其采样一个正样本和负样本, 这种采样操作在GPU 上不能被并行处理, 因而会花费很多时间; (2)在分批次训练中, 对于每个正负样本对, BPR 都要对其单独计算评分差, 然后通过非线性激活函数sigmoid, 得到一个正负样本对的损失, 然后再将所有样本对的损失函数求和。对多个样本损失函数求和的计算方式使得BPR 损失函数不能进行更好地向量化和矩阵化, 因此GPU 难以通过直接对参数矩阵操作展现其卓越的并行计算能力, 所以BPR 即使在GPU 上也难以通过分批训练提升效率。

3.3 实验分析

为了验证对BPR效率低下的原因分析, 我们在图神经网络推荐模型LightGCN 上进行了一系列实验。

首先要探讨负采样过程, 以及由非线性激活函数而导致的计算难以并行化对训练效率的影响。实验直接用LightGCN 工作公开的代码, 和主流推荐模型一样, 其工作以BPR 作为优化框架。我们采用Yelp2018 和Amazon Book(简写为Book)两个推荐系统中常用的数据集, 数据集的介绍详见5.1.1 节。我们将一次迭代中负采样的时间以及非线性激活函数消耗的时间展示在表1 中, 实验中非线性激活函数消耗的时间通过计算移除BPR 中非线性激活函数前后的时间差得到。

从表1 中可以发现, 在Yelp2018 数据集上, 一次迭代中负采样的时间大约占总时间的 1/5, 在Amazon Book 上负采样时间约占1/6, 可见负采样操作的确会在训练时消耗相当一部分时间。但与此同时, 移除了非线性激活函数之后, 训练的时间并没有显著下降。究其原因在于, 简单移除非线性激活函数并不能使BPR 的计算得到向量化和矩阵化, 即移除非线性激活函数之后, BPR 仍需要对每个样本对的损失单独计算之后再求和, 计算还是元素级别的,依然不能通过并行计算加速。因此为了提升训练效率, 必须在计算时引入更多向量化矩阵化的操作,从而更好地利用GPU 的并行计算性能。

表1 一次迭代BPR 中负采样和非线性激活函数操作的时间比较Table 1 Time comparison of negative sampling and nonlinear activation function in BPR in one epoch

为了验证上述想法, 我们人为地在计算中引入更多的向量化矩阵化等能够并行处理的操作, 我们对公式(1)加以修改, 并将其应用于LightGCN。引入并行操作的方法是: 给定一个训练批次中的一个用户, 采样T 个和他有过交互的物品和T 个和他没有交互的物品, 并最大化它们评分和之间的差距, 修改后的公式如式(3)所示:

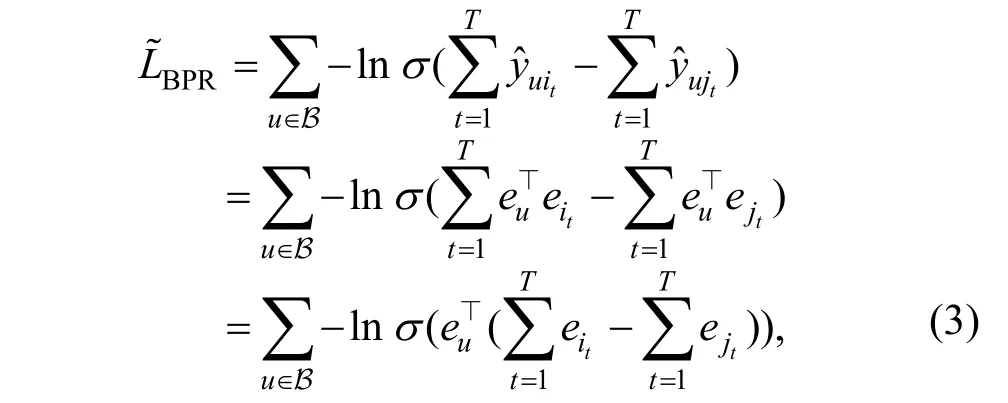
其中{it}和 { jt}分别表示用户u 有过交互的物品和没有交互的物品。显然, 原始的BPR 损失就是修改后的BPR 损失在T=1 时的特例。从修改后的公式中可以看出, 通过将非线性激活函数sigmoid 中的一个用户匹配多个正样本和多个负样本, 损失函数的计算将在通过非线性激活函数之前具有更高程度的向量化, 而向量化的计算能够更加充分地利用GPU的并行计算能力。

仍在LightGCN 工作的代码上进行实验。为了对比的公平性, 除对损失函数进行了如公式(3)的修改之外, 不对其他实验设置做任何更改。修改前后准确性和效率的比较分别展示在表2 和表3 中。

从表2 中可以看出, 随着T 的增加, 两个数据集上Recall@20 和NDCG@20 都在降低。这是在预料之中的, 因为BPR 经过了严格的数学推导论证, 直接将多个物品向量加起来再经过非线性激活函数没有理论保证, 不可避免地会对推荐的准确性表现产生负面影响。然而, 如表3 所示, 增加T 在两个数据集上都能够大大缩短训练时间, 比如在Amazonbook 上, T=1(即原始的BPR)时训练需要78.5 h, 而T=8 时下降到了37.2 h。这说明了原始的BPR 中, 每次将一个正负样本对的评分差单独通过非线性激活函数在GPU 上是很低效的。随着T 的增加, 越来越多正负样本对评分和的差值一起通过非线性激活函数, 增加了每次非线性操作之前计算的向量化程度,能够更好地利用GPU 的并行计算能力, 因此能够大大减少训练时间。

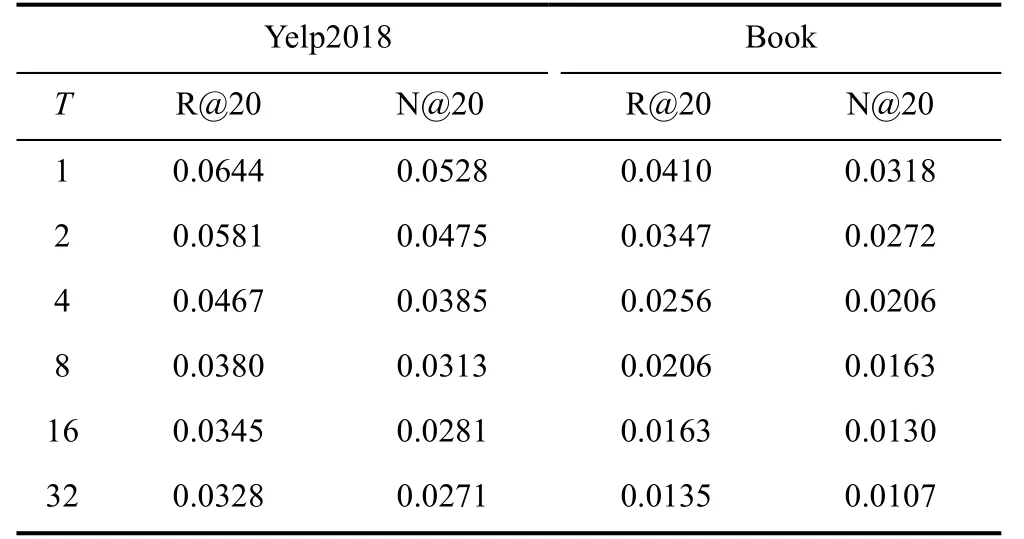
表2 修改前后BPR 损失函数推荐结果的比较Table 2 Performance comparison between the original BPR an revised BPR

表3 修改前后BPR 损失函数效率的比较Table 3 Efficiency comparison between the original BPR an revised BPRs

通过对实验现象的观察和上述的讨论可知: 原始BPR 的确存在效率低下的问题。修改后的BPR 由于在计算中增加了更多的向量化运算, 能更高效地利用GPU 的并行计算性能, 提高训练效率, 但鲁莽地在计算中增加向量化的操作并没有理论依据, 从而带来推荐准确性的损失。因此我们需要寻找其他策略, 来解决损失函数的计算中向量化矩阵化程度较低这一问题。

4 FGL

第三节我们对BPR 损失函数进行了深入研究,表明原始的BPR对GPU利用率低的问题存在于其公式之中, 修改后的BPR 虽然能够更加充分地利用GPU, 但却牺牲了推荐准确性。受以上发现的启发,本文致力于为推荐系统探寻新的优化框架, 使得在提高模型训练速度的同时, 保持推荐结果的准确性。

在不断地探寻中我们发现, 可以基于加权平方误差损失函数, 为推荐系统设计新的优化框架, 并基于应用全部负样本的策略, 经过严格的数学推导,将其转化为计算复杂度更低的矩阵运算的形式, 从而提高GPU 的利用率。我们将其命名为FGL(fast and generic learner)。

4.1 从平方误差到FGL

加权平方误差是在平方误差的基础上, 根据训练样本的重要性不同, 为其分配不同的权重, 是机器学习领域中常用的优化函数, 如公式(4)所示:

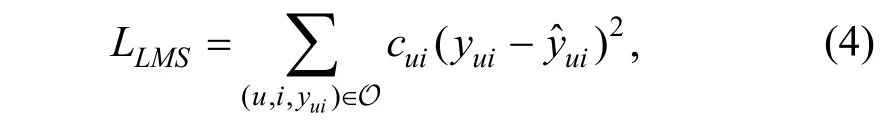
其中, O 表示所有训练样本的集合,既包含正样本又包含负样本。cui表示用户u 和物品i 对应的训练样本的权重, 其大小与对应样本的重要性有关。

将平方误差与推荐系统结合的思想最早可以追溯到文献[16], 作者简单将最小均方误差应用于推荐系统任务, 但由于当时GPU 计算尚未流行, 作者并没有做进一步分析, 更不用说推导出更适合GPU 运算的矩阵形式。最近的文献[9]采用了和文献[16]同样的思路, 改进的地方在于使用MLP 取代内积来计算用户对物品的预测评分, 对于损失函数的具体分析只进行了元素层面的推导, 也未进一步结合GPU 的特性进一步推导出矩阵层面的算法。

我们在文献[16]的启发下, 将平方误差与推荐系统结合, 以充分利用GPU 计算能力为目标, 最终得到了我们的方法FGL。

与BPR 相似, 考虑基于隐式反馈的推荐任务,即用户对物品的感兴趣程度是二值的, 只有喜欢和不喜欢之分, 那么有:

对于权重来说, 不同的交互可以体现用户不同的偏好, 比如购买比浏览更能体现用户的喜好, 因此不同训练样本的权重理应有所不同。同样基于隐式反馈的假设, 认为权重也是二值的, 将正样本的权重设置为α , 将负样本的权重设置为1, 即:

α 是我们引入的超参数, 将在实验部分对其加以研究。关于α 的取值, 正样本中的用户和物品是发生过交互的, 而负样本中用户和物品没有过交互,但没有交互也可能是因为物品没有曝光给用户, 即负样本中噪声较大, 因此正样本的权重应该比负样本的权重要大, α 的取值应大于1。

公式(4)中, 训练样本既包括正样本又包括负样本, 不同于BPR 中正负样本的比例为1︰1, 这里使用所有的负样本, 如此不仅可以节省负采样的时间,也有利于接下来的推导。基于以上讨论, 将推荐系统知识与应用在公式(4)中, 可以进行如式(7)中的推导:

其中, C 为常数, U 为所有的用户集合, I 为所有的物品集合,是由用户u 所有交互过的物品构成的集合,是由用户u 所有未交互过的物品构成的集合。式(7.a)是加权平方误差损失函数原始公式; 式(7.b)做了简单的展开; 式(7.c)中的常数是因为对于给定的数据集来说, 哪些用户对哪些物品产生交互行为是确定的, 因此上式中的第一项可以用常数表示; 式(7.d)中的第二项是因为在式(7.c)的第二项中,对于负样本来说 yui= 0, 因而可以只保留正样本,第三项和第四项是将式(7.c)中的正负样本分开; 式(7.e)是将式(7.d)中所有负样本预测评分的平方和,分解为所有样本的平方和减去所有正样本的平方和的形式; 式(7.f)是对具有相同求和下标的项进行合并。将常数项省略, 得到新的损失函数公式如式(8):

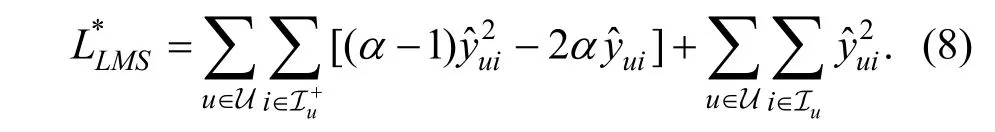
从求和范围可以看出, 式(8)的第一项是关于所有的正样本的求和项, 推荐系统数据集稀疏的特性使得第一项的计算复杂度很低; 第二项是关于所有的用户-物品对的求和项, 直接计算的话复杂度较高。之前的工作如文献[9, 16]仅仅止步于此, 仍然采用元素层面的运算, 不能充分利用GPU 的性能, 因此我们接下来将对其进行进一步的探究。

为了推导式(8)的矩阵计算形式, 我们先给出一些定义: 定义矩阵 P ∊R|U|×d为所有用户向量构成的矩阵, | U |为用户的数目, d 为用户向量的维度, 其中P 的第k 行表示第k 个用户的用户向量euk。同理定义 Q ∊R|I|×d为所有物品向量构成的矩阵, 每一行对应一个物品向量, 接下来对式(8)中第二项进行如下推导:

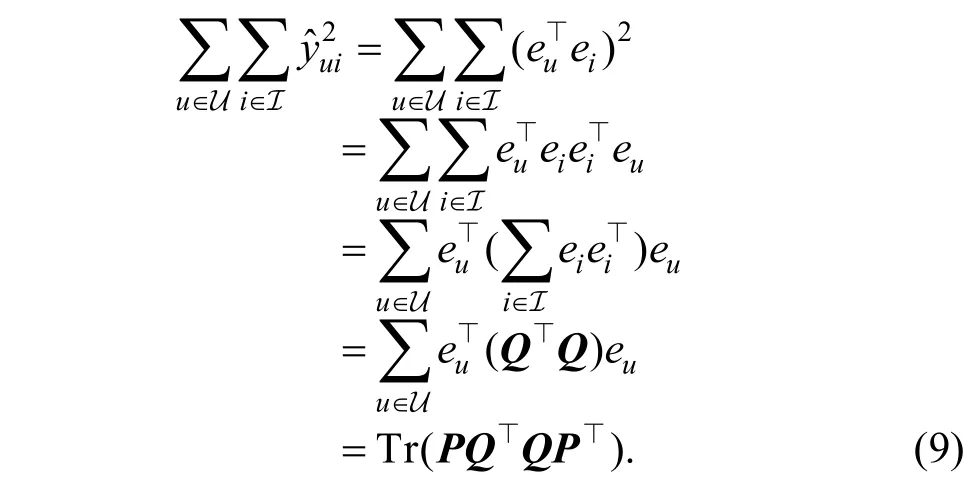
上式推导中用到了式(2)中给出的预测评分的定义, 以及矩阵迹的知识, 不再做详细解释。另外, 线性代数中矩阵的迹有如下性质: 对于两个维数适当的矩阵A 和B 来说:

应用这一性质, 我们对式(9)做进一步变换:

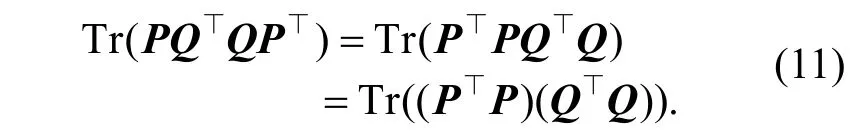
最终将FGL 的表达式写为:

容易看出, 损失函数的第一项包含了全部的正样本, 第二项是用户向量矩阵和物品向量矩阵的一系列线性操作。

式(9)～式(12)是我们工作的核心, 也是区别于文献[9, 16]的独到之处, 我们利用线性代数知识将复杂度很高的项转化为一系列矩阵的线性运算, 并利用矩阵迹的性质交换矩阵相乘的顺序。我们知道矩阵相乘的时间复杂度与相乘顺序密切相关, 而对矩阵的线性运算正是GPU 所擅长的, 因此 L*FGL很容易部署在当今常用的深度学习平台如TensorFlow 上, 并适合在GPU 上运行。

4.2 计算复杂度分析

我们将加权平方误差损失函数在推荐系统的框架下, 运用严格的数学推导, 最终得到了FGL 表达式如式(12)所示, 下面将对其进行计算复杂度分析。

直接分析使用所有负样本的情况。原始的平方误差如公式(4)所示, 其考虑了所有的用户-物品对,因为用户, 物品向量都是d 维的, 所以其计算复杂度为 O( | U || I| d)。从公式(4)到公式(7)仅仅是将推荐系统的一些假设应用于最小均方误差损失函数, 并省去了一些常数项, 理论上复杂度并未降低。真正降低复杂度是在公式(9)将矩阵的迹引入之后, 我们在公式(11)中应用了迹的性质, 改变了矩阵相乘的顺序。如果按公式(9)中的顺序进行相乘, 计算复杂度为O( | U || I |d + | U || I |d +| U || I | d ), 而按公式(11)中的顺序的话, 计算复杂度将变为 O(| U|d2+| I |d2+d3)。在实际的推荐系统数据集中, 用户和物品的数量相当, 能达到几万甚至几十万, 而推荐模型中用户和物品向量的维度一般不会超过256, 因此 d ≪| U |,| I |。所以式(9)的计算复杂度可以等效为O( | U || I| d ), 将远远大于式(11)的计算复杂度O( | U| d2)。以上都是对损失函数的第二项进行讨论的, 现在来讨论第一项, 推导前后(式(8)和式(12))第一项的复杂度均为 O(|O+| d), 从推荐系统数据稀疏的特性可以知道|O+|≪ | U || I |, 因而第一项的计算复杂度相比于第二项可以省略。由以上讨论可知, 经过严格的数学推导, 理论上FGL 的计算复杂度将大大降低。

另外, 由于GPU 能够对矩阵计算进行天然的并行加速, 而我们又通过严格的数学推导将加权平方误差损失函数中计算复杂度最高的项表示成了矩阵线性运算的形式, 因此FGL 能更充分地利用GPU 的性能。

4.3 与BPR 比较

对BPR 损失函数进行深入分析得出了BPR 效率低下的原因来自两个方面: 一是对每个正样本负采样得到一个负样本, 负采样过程会浪费GPU 资源；二是要对每个正负样本对的评分差单独通过非线性激活函数, 不利于GPU 进行并行加速。

而FGL 能够完美地解决上面两个问题: (1)FGL会使用所有的正负样本, 不用进行负采样, 从而不会因为负采样降低训练效率; (2)FGL 中复杂度最高的项是矩阵线性运算的形式, 能高效利用GPU 快速矩阵运算的特性。

此外, 从理论上, 相比于BPR 损失而言, FGL 在稀疏的数据上表现将会更好。原因在于BPR 中正负样本的比例是1︰1, 而FGL 会用到所有的负样本,即FGL 利用了更多的负样本, 从而理论上能够从负样本中学到更多有用的信息。数据集越稀疏, 负样本的比例就越大, 因此FGL 在稀疏数据集上将会有更好的表现, 这也是经过简单分析后得出的FGL 应用场景。实际中推荐系统的数据集往往非常稀疏, 因而预测FGL 在实际情况中会有更好的表现。我们将FGL 应用场景的深入研究留给未来工作。

5 实验流程与结果分析

为了评估FGL 的表现和效率, 并验证FGL 的适用场景, 我们在4 个来自实际的数据集上进行了大量的实验。

5.1 实验设置

5.1.1 数据集

实验中使用了4 个来自真实世界的数据集:Yelp2018, Amazon Book(简写为Book), Amazon Office Products(简写为Office), Amazon Cellphones and Accessories(简写为Cellphones)。其中前两个选自自LightGCN 工作, 用户-物品交互较为稠密。为了体现我们的方法在大规模场景下的优势, 并比较数据集稀疏度对方法的影响, 我们另选取Amazon 数据集的2 个子集, 相较于前2 个数据拥有更大的用户物品基数, 但是用户物品交互较为稀疏。我们在表4 中展示了数据集的统计特性:

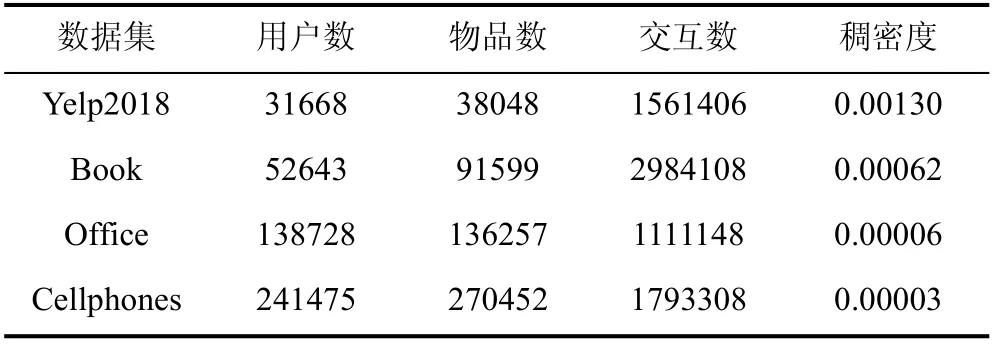
表4 数据集统计特性Table 4 Statistics of the datasets

下面对数据集进行简要介绍:

(1) Yelp2018: 数据来自2018 版本的Yelp Challenge, 其中餐馆、酒吧等被当作物品。

(2) Book, Office, Cellphones: 数据来自著名推荐数据集Amazon review, 3 个数据的物品分别是书籍,办公用品, 和手机等电子产品。

对于每个数据集, 我们从每个用户历史交互物品中随机挑选80%作为训练集, 其余20%作为测试集。

5.1.2 模型介绍

我们在实验中使用了推荐系统中经典的图模型MF, 和目前最先进的基于图卷积网络的推荐模型LightGCN:

(1) MF[1]模型中, 用于计算评分的用户向量和物品向量通过随机初始化得到, 并在训练时对它们进行优化。

(2) LightGCN[7]模型中, 先随机初始化一组原始的用户向量和物品向量, 用于计算评分的用户,物品向量通过原始向量经过用户-物品交互二分图进行图卷积得到, 图卷积的层数与LightGCN 的层数相对应。

5.1.3 评价指标

模型训练之后, 对于每个用户, 我们对其所有未在训练集中交互的物品计算预测评分, 然后按评分由高到低对这些物品排序, 挑选出排在前N 位的物品, 作为预测的用户感兴趣的物品, 即推荐系统中常用的 Top-N 评估[8], 具体评价指标采用Recall@N 和NDCG@N[6], 其中Recall@N 只考虑了用户在测试集中感兴趣的物品有没有在前N 位出现,而不考虑出现的位置先后; 而NDCG@N 不仅考虑了预测前N 位中真正感兴趣的物品的比例, 还要考虑相对位置因素, 认为把感兴趣的物品排得靠前的模型要更好。实验中取N 为20 和100。计算出每个用户的指标后, 对所有的用户取平均得到总指标。

5.1.4 超参数设置

所有的实验都在TensorFlow 平台实现。在数据集Yelp2018 和Book 上, 用户和物品向量的维度设置为64; 其他两个数据集Office 和Cellphones 规模较大, 用户物品数量都多达几十万, 因而将物品向量的维度设置为16, 以避免内存不足的问题。对于BPR来说, 采用分批训练的策略, 每批的大小(batch size)为1024。两个方法优化器均使用Adam。学习率等超参数采用网格搜索的策略选择最优的, 学习率从{0.001,0.01}中选择效果最好的; 均采用 L2正则化,正则化系数从 {e-5, e-4, e-3,e-2, e-1}中选择效果最好的。我们在FGL 中引入了一个新的超参数α 来表征正样本的权重, 经过讨论α 取值应该大于1, 因此在实验中搜索α 的范围为: {10,20,…,100}。对于LightGCN 模型, 不失一般性, 下面展示了2 层和3层的结果。

5.2 训练效率比较

本节将进行FGL 与BPR 损失函数的效率比较,为了尽可能保证比较的公平性, 所有的实验都在相同的GPU(GTX 1080Ti)上进行。我们把在四个不同的数据集上, 采用不同的图推荐模型的比较结果展示在表5 中。

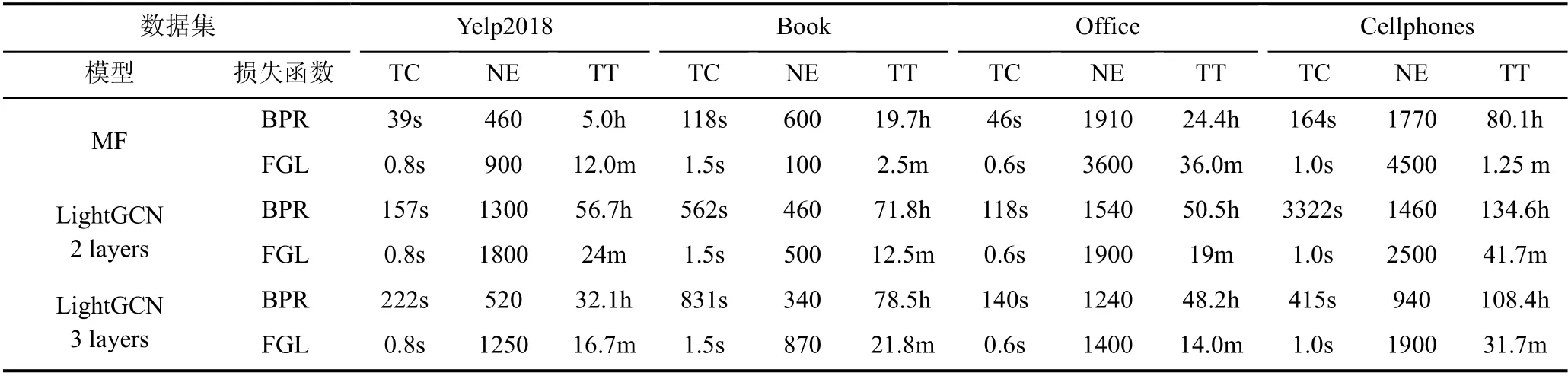
表5 BPR 与FGL 的效率比较Table 5 Efficiency comparison between BPR and FGL

从表5 中有一些重要的发现。首先, 对于每次迭代的训练时间来说, 从MF 模型到2 层LightGCN再到3 层LightGCN, 随着模型复杂度的增加, FGL每次迭代的时间几乎不变, 而BPR 每次迭代的时间大幅增加。比如在数据集Yelp2018 上, 采用BPR 损失函数, LightGCN 的层数从2 层增加到3 层, 每次迭代的时间从157s 增加到了222s; 而采用FGL 每次迭代的时间都在0.8s。两种优化框架不同的计算方式很好地解释这一现象。FGL 的计算是一系列矩阵的线性运算, LightGCN 中也恰好去掉了图卷积网络中的非线性激活函数, 因此即使随着层数的增加,LightGCN 的计算也是线性的, 所以即使层数增加了, 依然能够充分利用GPU 的性能。但是非线性计算在 BPR 损失中占据了很大一部分, 随着LightGCN 层数的增加, 对GPU 利用率低下的问题会越来越明显, 因此BPR 每次迭代的时间会随着层数的增加大幅增加。

在总训练时间上, FGL 损失相比于BPR 损失来说可以将训练速度提升几个数量级。虽然FGL 会进行更多次数的迭代才能收敛, 但每个迭代耗时极少,因此总的训练时长非常短。比如在数据集Book 上,模型用三层的LightGCN 时, BPR 需要78.5h 才能收敛, 而FGL 只需要21.8min, 即FGL 将训练时间从数天缩短到了不到0.5h。因为两种方法只有优化框架上的差异, 因此我们可以得出结论: FGL 相对于BPR 损失来说的确能带来训练速度的极大提升。

5.3 准确性比较

上一节比较了FGL 和BPR 的训练效率, 得出FGL 在效率上具有巨大的优势。本节将进一步比较两种方法的推荐准确性, 以说明FGL 效率的提升并没有以牺牲推荐准确性表现为代价。准确性的表现总结在表6 中。

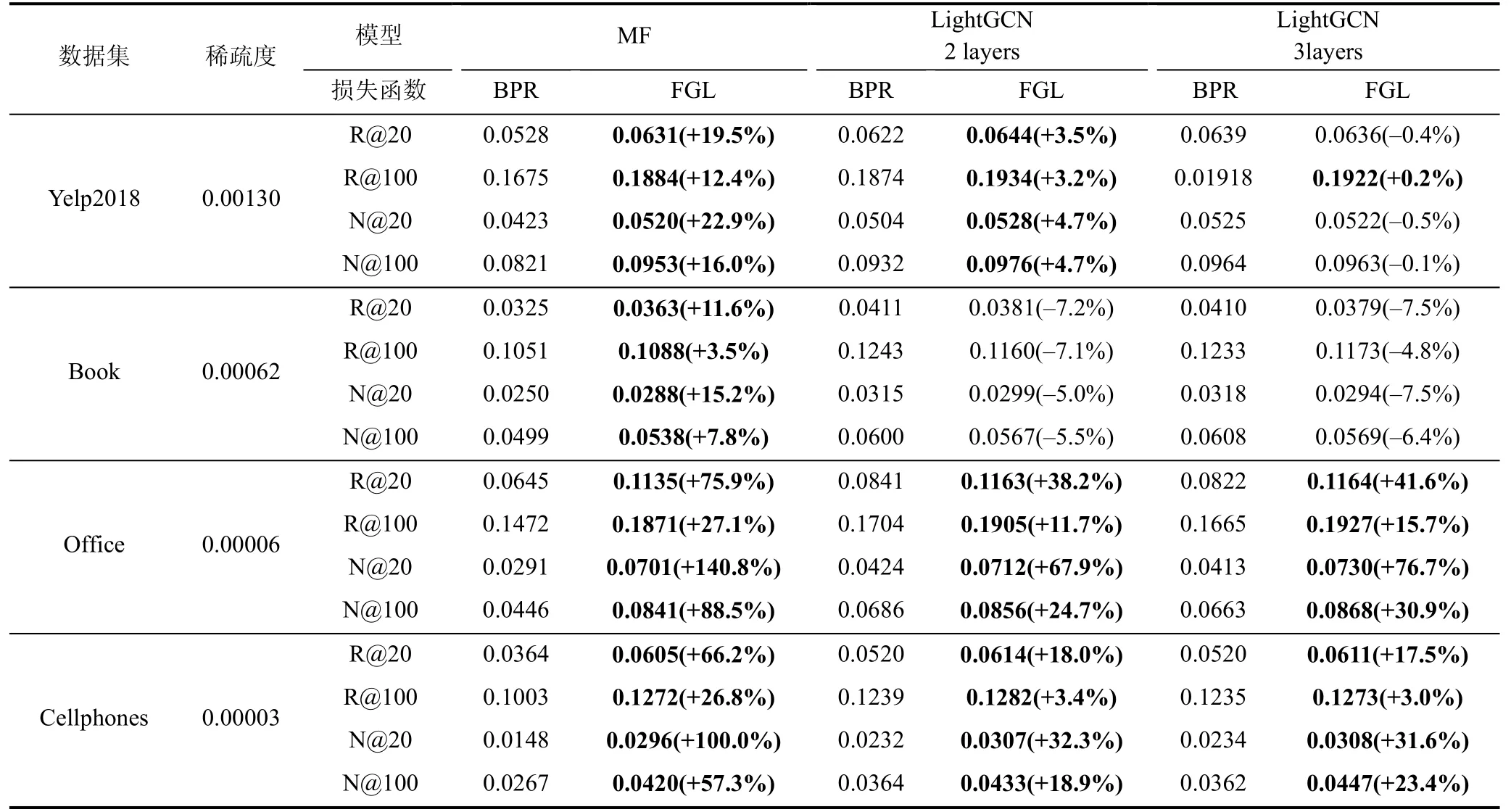
表6 BPR 与FGL 的推荐准确性比较Table 6 Recommendation accuracy comparison between BPR and FGL

从表6 中可以看出FGL 的表现在Yelp2018 和Book 数据集上取得了和BPR 不相上下的结果, 在Office 和Cellphones 数据集上, FGL 推荐结果明显好于BPR。于是可以认为: FGL 在加快训练速度的同时,并不会损失推荐结果的准确性。

虽然能看出FGL 推荐准确性不逊色于BPR, 但在不同的数据集上, 性能出现了明显的差异, 这促使我们进步分析其原因, 以给出FGL 的适用场景。经过分析之后, 我们将其归因于数据集之间不同统计特性带来的差异。之前提到过, Yelp2018 和Book数据集直接来自于LightGCN 的工作, 我们了解到作者在处理这两个数据集的时候, 只保留了原始数据中拥有10 个以上交互的用户和物品, 从数据集的统计特性中我们也可以看出, 这两个数据集更为稠密。而本文为了得到规模更大的数据集, 在处理Office和Cellphones 数据集时, 保留了拥有5 个以上历史交互的用户, 物品不做过滤, 因此后两个数据集更为稀疏, 并保留了物品长尾分布的特性。而我们知道实际场景中推荐数据集往往非常稀疏并且长尾效应明显, 根据之前的分析, FGL 能够利用全部负样本信息,因此将在这种情况下取得更好的效果。

5.4 超参数研究

我们在FGL 中引入了超参数α , 用来表示正样本的权重, 本节将研究α 对于推荐结果的影响。不失一般性, 将使用2 层LightGCN 模型, 在Yelp2018 和Cellphones 数据集的表现绘制在图1 中。

从图1 中可以看出, 不同的α 会对推荐结果产生很大的影响, 这也说明了在FGL 中, 平衡正负样本对得到较好的推荐结果来说至关重要。此外, 在不同的数据集上, 达到最好表现的α 也不相同, 对于Yelp2018 数据集, 在α 取30 时达到最好表现; 而对于Cellphones 数据集, 最好的α 是90。因此在实验或应用中, 使用FGL 时, 应该认真调整α 以得到最好的推荐效果。

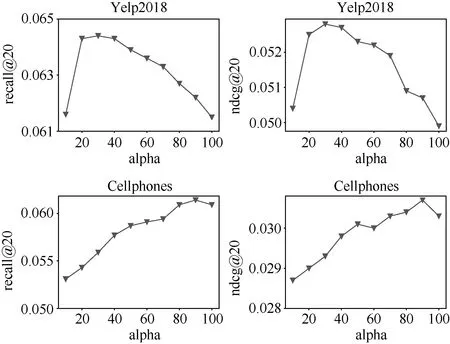
图1 2 层LightGCN 的推荐结果在Yelp2018 和Cellphones 上随α 变化的曲线Figure 1 Performance of 2-layer LightGCN w.r.t.different α on Yelp2018 and Cellphones

6 结论与未来工作

在本文中, 我们指出随着深度学习, 尤其是图卷积网络在推荐系统中的应用, 以及在GPU 上进行模型训练的流行, 用BPR 损失函数进行模型参数优化十分低效, 原因在于BPR 对每个样本都要进行非线性变换, 缺乏矩阵化和向量化的计算, 浪费了GPU 的并行计算性能。为了验证这一想法, 通过将多个样本的评分求和之后, 再通过非线性激活函数的方法, 我们人工地在BPR 中加入向量化运算, 这种做法的确会使训练速度得到提升, 但是不出意外的损失了推荐的准确性。为了克服这一问题, 必须寻找BPR 以外的优化框架。我们发现通过在推荐系统中引入加权平方误差损失函数, 加以严格的数学推导, 能够将其转化为一系列矩阵线性运算的形式,并且可以利用线性代数的知识改变矩阵运算的顺序,进一步降低其计算复杂度。据此我们提出了FGL:一种快速且普适的学习框架。除在计算方面更为高效外, FGL 还节省了BPR 中负采样的时间。我们在四个真实数据集上进行了大量的实验, 结果表明在保持推荐准确性的情况下, FGL 能够大大提高训练效率。

未来我们将对这个工作的探索分为两个部分:一是寻找更合适的应用场景, 我们在简单分析后得出FGL 在数据集稀疏, 并且具有长尾特性时表现很好, 我们将在这方面进行更多研究, 以给出更具有指导意义的结论; 二是FGL 中引入了超参数α , 现在采用网格搜索的方法寻找最优值, 我们将研究能否采用更快捷的策略, 如自适应方法等来选择α 。