可压缩两相流固耦合模型的间断Galerkin 有限元方法1)

2021-11-10马天然沈伟军刘卫群XuHao

力学学报 2021年8期

关键词：辽金饱和度边界

马天然沈伟军 *†,2) 刘卫群 Xu Hao

* (中国矿业大学力学与土木工程学院,江苏徐州 221116)

† (中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州 221116)

** (中国科学院力学研究所,北京 100190)

†† (中国科学院大学工程科学学院,北京 100049)

*** (劳伦斯伯克利国家实验室地球科学部,美国伯克利 94720)

引言

深入探索多孔介质中多相流动和固体变形特征对精准认识地下资源开发利用,例如石油勘探开发、煤层气和页岩气开采、二氧化碳地质封存等领域,具有重要的工程意义[1-4].在流体输送过程中局部压力和饱和度梯度下的渗流作用改变了孔隙结构特征,打破了储层内部的水力平衡;固体空间结构的变化影响了储层内部流体的运移路径和流通能力,具体表现为多孔介质孔隙度和渗透率等物性参数的动态响应.发展和建立两相渗流与固体变形耦合模型及其相应的数值方法是准确描述和阐明储层内水力行为的有效手段[5-7].

针对两相渗流和固体变形耦合模型的数值方法主要包括有限元法[8-10]、有限体积法[11-12]以及混合计算方法[13-14]等.对于两相流问题的离散和数值求解,传统有限元能够确保流体域内整体的质量平衡,但是无法实现流体在跨越单元间的局部质量平衡,因此不适用于求解对流占主导的非线性不混溶问题;有限体积法在确保局部流量平衡的同时,具有较高的计算效率,因此在工业界和工程尺度模拟中得到了广泛应用.在通常情况下,有限体积方法的计算结果仅能满足低阶有效精度;混合计算方法是指对流体和力学控制方程分别利用不同的数值方法进行求解,该方法集成了各种数值方法的优势.Rutqivst[15]在耦联流体软件TOUGH2 和固体变形软件FLAC3D的基础上,开发了在油气、地热、可燃冰开采以及二氧化碳地质封存等领域广泛使用的TOUGH-FLAC耦合模拟器.在此模拟器中,负责流体计算的TOUGH2 软件采用的是有限体积法,FLAC3D 采用有限差分法计算固体变形,此方法在网格划分和数据传递效率等方面具有一定的局限性.

如何在刑事立法政策的制定过程中辩证地认识民意，正确引导民意、有效利用民意是一个需要亟待解决的问题。然而民意的定义与范围十分抽象、复杂，甚至真伪难辨，一旦研判失误，极易误导决策者，甚至可能造成社会混乱。因而对民意的考量必须加以合理的规制。

间断伽辽金有限元(discontinuous Galerkin finite element method,DG-FEM)结合了有限体积与有限元两种方法的优点,具有高阶精度和局部单元物理守恒性的特点,容易实现局部网格加密和各单元多项式的单独选取[16-19].近些年来,DG-FEM 在流体和弹性力学领域得到了广泛的关注和持续的发展[20-22].Klieber 和Riviere[23]在解耦两相渗流微分方程组的基础上,提出了不可压缩两相流自适应间断有限元方法.Epshteyn 和Rivière[24]提出了多孔介质不可压缩两相流完全隐式方程的不连续伽辽金方法,该方法在结构化和非结构化网格计算中都具有较好的鲁棒性.李子然和吴长春[25]、陈韵骋等[26]建立了基于线弹性力学问题的局部间断有限元方法.在流固耦合方面,Liu 等[27-28]提出了连续和间断伽辽金耦合框架,利用自适应加罚方法提高间断伽辽金有限元方法在模拟大型多孔弹性问题时的适用性和计算效率,并将此方法推广至多孔介质水力压裂模拟中.目前关于间断伽辽金有限元方法在计算可压缩两相流固模型方面的研究鲜有报道,还有待进一步深入研究.

随着社会经济的不断发展以及人们生活水平的不断提高，对道路桥梁工程的施工质量的要求也越来越严格。为了满足社会发展的需要，以及人们交通出行的需求，应不断提高道路桥梁工程的建设质量。因此，保证道路桥梁工程原材料的质量成为保障工程建设质量的基础与前提。

利用上述类似的推导过程和方式,可以得到式(2)的间断伽辽金弱形式,如下所示

1 两相流固耦合控制方程

1.1 两相渗流方程

假设模型中湿润相和非湿润相为不混溶流体,两者在多孔介质中的流速满足达西定律.在考虑毛细压力、重力效应和固体变形的基础上,等温可压缩两相渗流控制方程可表示为[2,29]

式中,下标β 为w和 n w分别表示湿润相和非湿润相,Sβ为饱和度, ρβ和µβ分别为流体密度和黏度,Cβ为流体压缩系数,pβ为流体压力,k为多孔介质绝对渗透率张量,krβ为相对渗透率,Qβ为源汇项, εv为体应变,pc和 |pc|分别为毛细压力和毛细压力对湿相饱和度的导数.

针对学校知识资产的存在形态与管理目标，结合信息系统分析与设计、文档一体化管理、关系数据库系统等原理，高校机构内知识资源综合管理平台的结构设计，整体上应该包括系统用户管理、各职能部门应用子系统管理、知识档案资源数据库管理、知识库增值服务管理等四大管理模块。

为了求解方程,需要补充如下辅助公式

式中,pe为毛细管吸入压力,Se为有效饱和度, λ 为孔径分布指数,Srw和Srnw分别为湿润相和非湿润相的残余饱和度.

此外,选取Genuchten−Mualem 相对渗透率模型描述湿润相和非湿润相的流通能力,表达式如下所示[30]

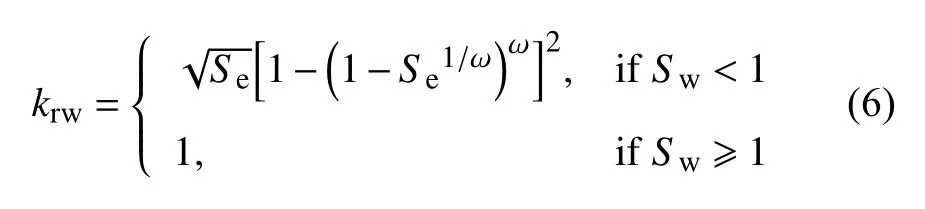
模型的初始条件为

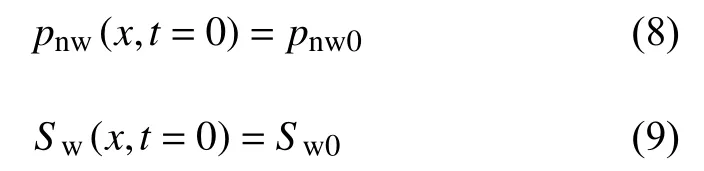
模型中Dirichlet 和Neumann 边界条件如下所示

进入防汛物资管理界面可对各仓库进行防汛物资库存情况查询，网上申请、审批发放管理，对购置入库、维修保养、出入库时间记录列表上传、下载进行物资仓库管理。

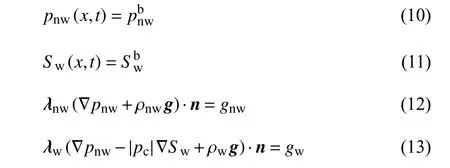
1.2 两相渗流方程的间断伽辽金弱形式

图1 为模拟几何区域、边界条件和网格示意图.在计算域 Ω中,边界 ∂ Ω由不与内部单元接触的外边界 ∂ Ωo和内部相邻单元共享的内边界 ∂ Ωi两部分组成.由图1 可知,内边界 ∂ Ωi为相邻单元E+和E−共同拥有;外边界∂Ωo由Dirichlet 边界∂ΩoD和Neumann 边界 ∂ ΩoN两者构成,即 ∂ Ωo=∂ΩoD∪∂ΩoN.设是区域 Ω的正则剖分, ∂E=∂Ωo∪∂Ωi表示为所有边界的集合,则间断有限元空间定义为

图1 几何区域、边界条件和网格示意图Fig.1 Domain with boundary conditions and mesh skeleton

式中,离散空间pr(E)为单元E上不超过r次的多项式的集合.

为了推导两相渗流方程的间断伽辽金弱形式,首先在式(1)等号的两侧乘以试函数并在单元计算域E内进行积分,可得到

利用分部积分和散度定理,式(15)中等号左侧第二项可表示为

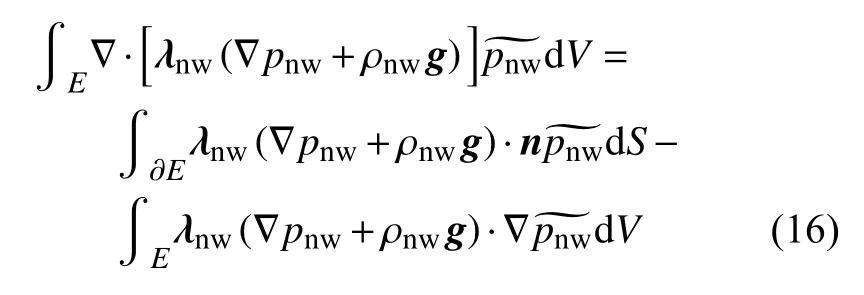
方程式(19),式(20)和式(27)是多孔介质中可压缩两相渗流和固体变形的弱形式.本文利用通用有限元软件COMSOL Multiphysics 内置的Weak Form PDE 模块求解可压缩两相流固耦合模型.基于二次不连续拉格朗日形函数构建对解域的间断伽辽金有限元逼近,选取向后差分公式(backward differentiation formula,BDF)隐式求解器.其中,BDF 求解器采用自适应时间步长算法和可变离散化阶数,离散化的BDF 精度从1～5 不等.基于LU 分解,采用MUMPS (multifrontal massively parallel sparse)直接求解器对线性系统进行求解,并选取完全耦合的求解器(fully coupled solver)将线性求解器应用于牛顿单步法的非线性问题.默认情况下,初始时间步长设置为结束时间的0.1%,相对容差为0.01.

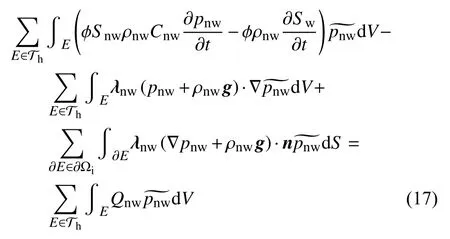
水还没消下去，杨小水却坚持要回去。一路上看到的树，树梢上都挂满了水草。第二天进入遂平境内，连树都少见了。大的多伏在地上，小的，连根都拔走了。老鼠都圆滚滚的，像小孩子玩的皮球，也不怕人，在地上缓缓地滚动。铁路线这边的路沟里，是她这辈子见过尸体最多的地方。层层叠叠地摞着，不计其数。附近的树枝上落满了苍蝇，黑压压的，把树都压弯了。

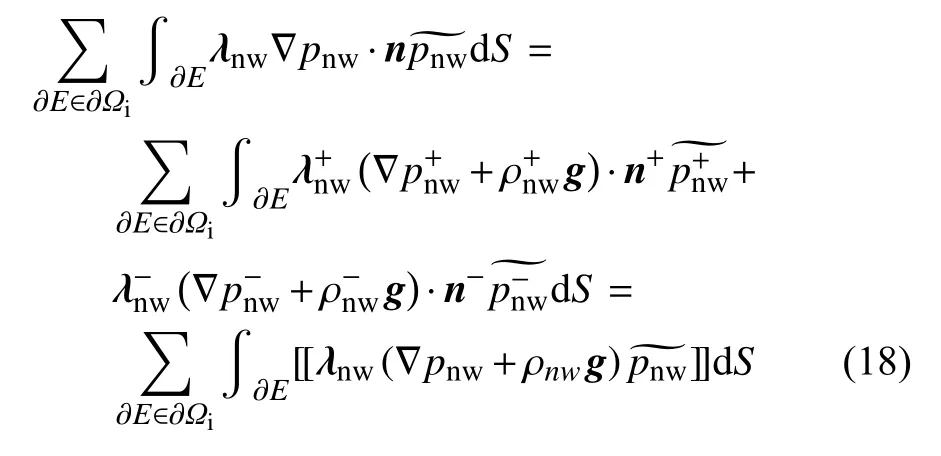
将式(18)代入式(17)中,结合稳定项、加罚函数项以及相应边界条件,可得

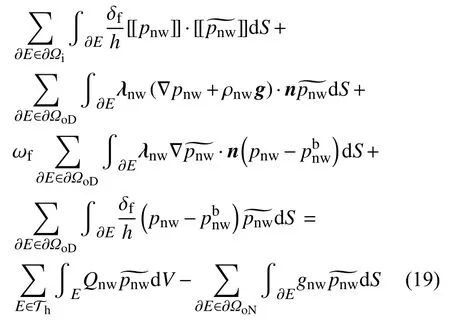
基于上述认识,本文首先建立可压缩两相流固耦合控制方程,其中包括考虑毛细压力和重力作用的可压缩两相渗流方程以及线性多孔弹性方程.在此基础上,推导出流固耦合方程的间断伽辽金弱形式;然后,通过一维Terzaghi 流固问题验证模型的准确性;最后,分别开展二维平面应变条件下和考虑重力效应的三维流固数值算例,分析流体压力、饱和度以及固体应力、位移的分布特征,探讨加罚因子对模拟结果的影响.

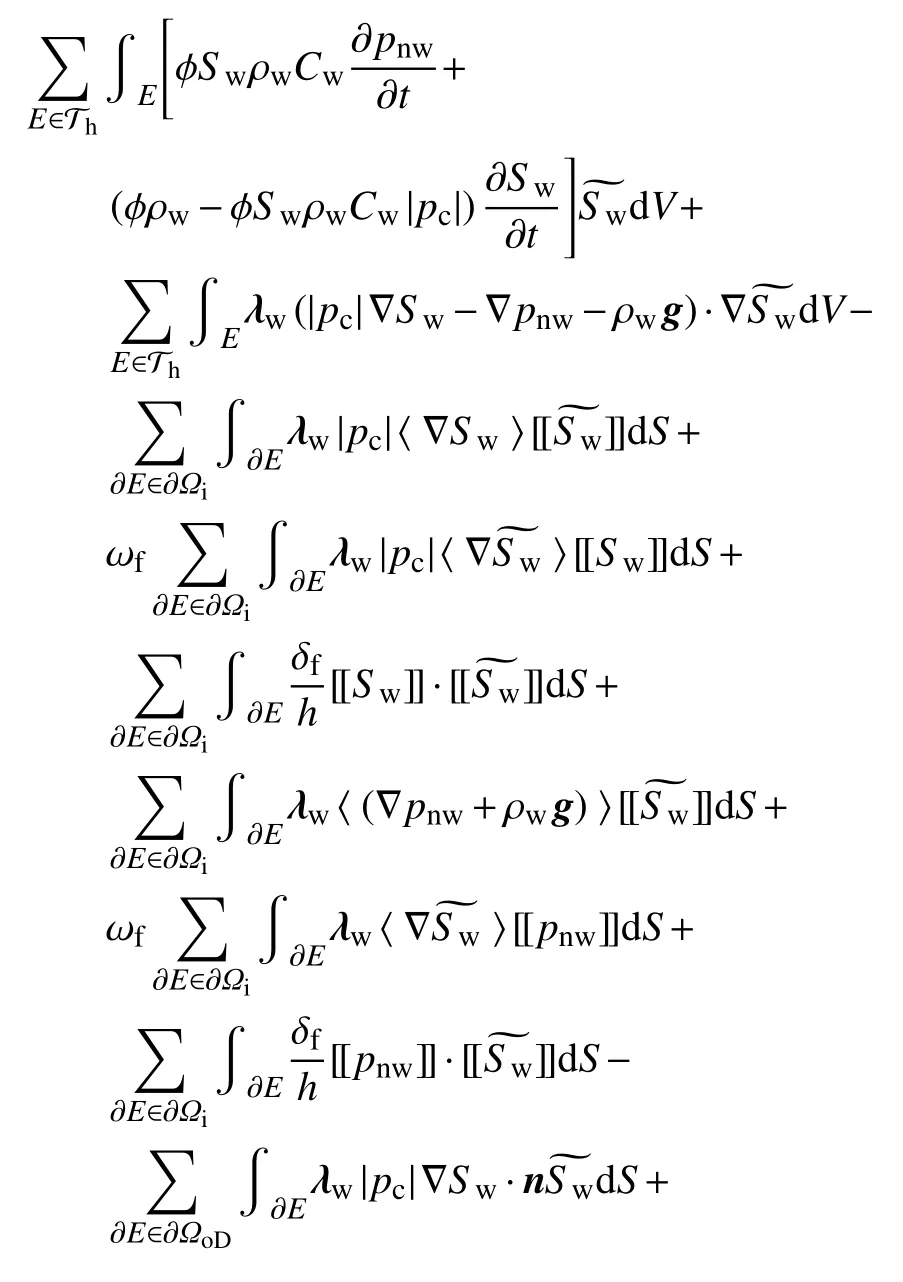
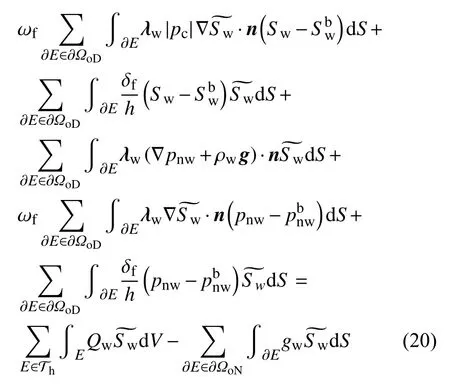
式(19)和式(20)为考虑固体变形作用下可压缩两相渗流方程的间断伽辽金有限元方法的弱表达形式.

大学生作为独特的社会群体，其思想活跃、充满创意意识，并由此形成了别具特色的校园文化。基于此，高校的教育教学中，应将社会主义核心价值观融入到校园文化中来，利用校园文化活动，为大学生的思想价值培养提供良好的外部环境。例如在校园文化建设中，学校可以组织社会主义核心价值观的专题讲座，做好理论宣传；组织社区志愿活动，让学生在社区服务中强化社会责任感；组织专业实习，将学校教育与职业需求相结合，提高大学生的自我认识；参与社会调查，从政治、文化、经济、生态等多角度了解社会，让大学生从书本中走出来，提高社会实践能力。

（4）止水带压板采用“凵”型钢板，在螺帽和压板之间设置弹性垫圈，调整定位后拧紧。螺帽以上紧为准，原则上紧固力为3kg，一般不宜超过5kg，但不应小于2.5kg。螺栓外露部分采用塑料套保护。此种钢板刚度较“一”型成倍增加，拧紧螺栓时不会因压板变形而产生漏水空洞。

1.3 固体变形方程及其弱形式

假设多孔介质固体变形满足弹性小变形条件,那么固体变形的平衡方程、几何方程、本构方程以及边界条件如下所示

式中,总应力 σ =σ′−αIp,则式(21)可改写

2.3.1 产前遗传咨询及产前诊断情况截止到2016年11月，通过电话随访及门诊回访232对夫妻进行了进一步的遗传咨询并对丈夫相关基因进行了检测。其中同基因携带为33例，其中2例暂未怀孕，18对夫妻经知情同意选择进一步产前诊断，其余拒绝产前诊断。

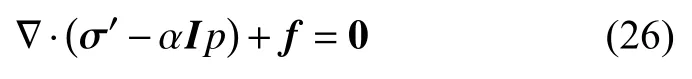
式中, σ′为有效应力张量, ε为应变张量,u为位移张量,f为体积力张量, α 为Biot 常数,D为4 阶弹性张量,I为单位张量,平均孔隙压力p=Snwpnw+Swpw.

本节利用间断伽辽金方法开展在二维平面应变条件下两相渗流和固体变形耦合数值计算.在本算例中,分别选取水和氢气作为湿润相和非湿润相.模型的几何尺度、初始条件、边界条件和监测线如图4 所示.模型的长度和宽度均设置为10.00 m.多孔介质的弹性模量和泊松比分别为10.00 GPa 和0.30;渗透率和孔隙度分别设定为 1 .00×10−14m2和0.20.模拟区域的初始气体压力为4.00 MPa,初始水饱和度为0.80.模拟左边界和下边界为位移约束,在上边界和右边界分别施加 − 1.00 × 107MPa (负号表示压应力方向)的垂直和水平应力.模型左下角为注入边界,设置注入的氢气压力和水饱和度分别为5.00 MPa 和0.80;右上角为出口边界,出口气体压力和水饱和度设置为4.00 MPa 和0.20.

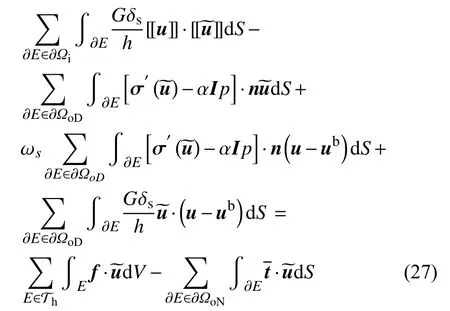
1.4 数值方法的实现

将式(16)代入式(15),累加所有单元区域,可得

2 模型验证

图2 描述了一维Terzaghi 固结问题的几何示意图以及相应的边界条件.为了确保孔隙压力沿上下两端保持为零,设置模型上下两端为排水边界.在模型上边界瞬间施加均布载荷q=−5.00 MPa.本模型长度 2h=10.00 m,其他参数的具体取值如下[2]:剪切模量为30.00 GPa,压缩模量为50.00 GPa,多孔介质渗透率为 1 .00×10−12m2,孔隙度为0.25,流体压缩系数为 1 .00×10−12Pa−1, 流体黏度为 1 .00×10−3Pa·s,加罚因子 δf和 δs分别设置为1.00 和10.00[31].

干法电选是利用粉煤灰在高压电场作用下，因灰与炭导电性能不同而进行的分离。粉煤灰是非导体物料，炭粒是良好的导体物料，在圆形电晕电场中，当粉煤灰获得电荷后，炭粒因导电性能良好，很快地将所获电荷通过圆筒带走，在重力惯性离心力作用下，脱离圆筒表面，被抛入导体产品槽；而非导体的粉煤灰所获电荷在表面释放速度较慢，故在电场力作用下，吸收在圆筒表面上，被旋转圆筒带到后部，由卸料毛刷排入非导体产品槽中，从而达到灰炭分离的效果。

随着社会经济和医药产业的发展及公众日益增长的健康需求，医药新产品、新剂型层出不穷，例如中药材的新型产地加工或炮制加工品种、中药配方颗粒、中药精制饮片超微细粉加工等，相应的产品质量标准研发需求旺盛。药品检验机构作为药品监管和产业发展的重要技术支撑，承担着大量的注册检验、监督抽检、仿制药一致性评价复核检验、质量标准制修订和补充检验方法研制等检验检测和技术研究任务，是新时代市场监管和医药产业发展不可或缺的技术力量。如何充分发挥药检机构在质量标准研究方面的技术优势，为市场监管、产业发展和推动“放管服”提供技术支撑，值得深入研究。

图2 Terzaghi 固结问题几何示意图Fig.2 Sketch of Terzaghi’s consolidation problem

图3 为Terzaghi 固结问题的理论解[32]和DG有限元数值解的比较.结果显示,DG 有限元计算得到的数值解与理论解吻合较好,进而验证了间断伽辽金方法在求解流固耦合方程时的可行性和有效性.

在间断伽辽金方法中,变量在单元内边界 ∂ Ωi处满足不连续设定,因此式(17)中等号左侧第三项可以改写为

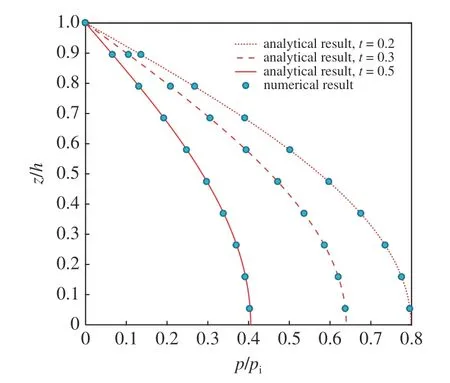
图3 Terzaghi 固结问题理论解和数值解的比较Fig.3 Comparison of the analytical and numerical results for Terzaghi’s consolidation problem

3 算例分析

3.1 二维平面两相流固算例

利用类似式(19)和式(20)的推导过程,结合相应的边界条件,可以得到固体变形方程的弱形式,如下所示

图4 模拟几何尺度、初始和边界条件Fig.4 Simulation geometrical configuration with boundary and initial conditions

数值模拟分两个阶段开展.首先,开展储层力学和流体平衡的稳态计算.然后,将第一步计算得到的应力和孔压等水力信息作为含水层氢气注入模拟算例的初始条件.整个模拟时间为1500 s,其他变量的具体数值如表1 所示.

图5 和图6 分别给出了注气第1500 s 气体压力pnw、水饱和度Sw、水平位移u和水平有效应力的空间分布云图以及变量沿监测线的分布图.由图5和图6 可知,随着氢气的持续注入,气体压力影响范围扩大至距注入边界7 m 左右,并引起固体膨胀变形且变形影响范围扩散至边界处.究其原因是因为在多孔弹性介质中位移或者应变可传播到压力前沿之前.受毛细压力和气水两相物理属性差异的共同影响,氢气主要聚集于注入边界附近.在多孔介质内孔压在远离注入边界的过程中呈现递减趋势,而有效应力沿监测线增加.

图6 第1500 s 时气体压力 pnw、水饱和度 Sw、水平位移 u 和水平有效应力沿监测线的分布Fig.6 The profiles of gas pressure pnw,water saturation S w ,horizontal displacement u and horizontal effective stress along the monitoring line at t = 1500 s

3.2 加罚因子的影响

图7 给出了 δs=0.10,1.00 和10.00 时水平位移u和水平有效应力沿监测线的分布.图8 给出了δs=0.10时水平位移u和水平有效应力 σ′x的分布云图.图9 给出了 δf=0.01,0.10,1.00 和10.00 时气体压力pnw、水饱和度Sw沿监测线的分布.结果表明,不同加罚因子条件下,变量u,,pnw和Sw沿着监测线的变化趋势大体保持一致.在计算固体变形时,计算结果对加罚因子的选取更为敏感.当 δs= 0.10时,应力和位移均在局部出现明显的波动;当 δf=0.01 时,饱和度在小范围内发生轻微浮动.这主要由于加罚因子 δs和 δf的降低减少了自变量位移、压力以及饱和度在单元处弱连续性的约束,造成了变量局部波动的现象.通过适当提高加罚因子可以加强变量在跨越单元交界面处的连续性,但是较高的加罚值会引发病态条件矩阵的可能性.

图7 第1500 s 时不同加罚因子 δs条件下水平位移 u 和水平有效应力沿监测线的分布Fig.7 The profiles of horizontal displacement u and horizontal effective stress along the monitoring line at t = 1500 s with different values of penalty parameter δs

图8 第1500 s 时 δs=0.01水平位移 u和水平有效应力分布云图Fig.8 The distribution of horizontal displacement u and horizontal effective stress with δs=0.01 at t = 1500 s

图9 第1500 s 时不同加罚因子 δf条件下气体压力pnw 、水饱和度Sw 沿监测线(0,0.05)−(10,9.95)的分布Fig.9 The profiles of gas pressure pnw and water saturation S w along monitoring line at t = 1500 s with different values of δf

值得注意的是,受流体边界条件、初始条件以及流体方程的非线性特征等因素的影响,传统有限元方法在求解本节流体模型时无法收敛,此情况在一定程度上体现了间断伽辽金有限元在求解可压缩两相流固方程上的优越性.本节将传统有限元的计算结果作为基准方案,通过比较间断伽辽金有限元和传统有限元两者计算得到的水平位移和水平有效应力之间的相对误差,分析加罚因子 δs对计算结果的影响.水平位移和水平有效应力的计算误差erru和errs的表达式为[33]

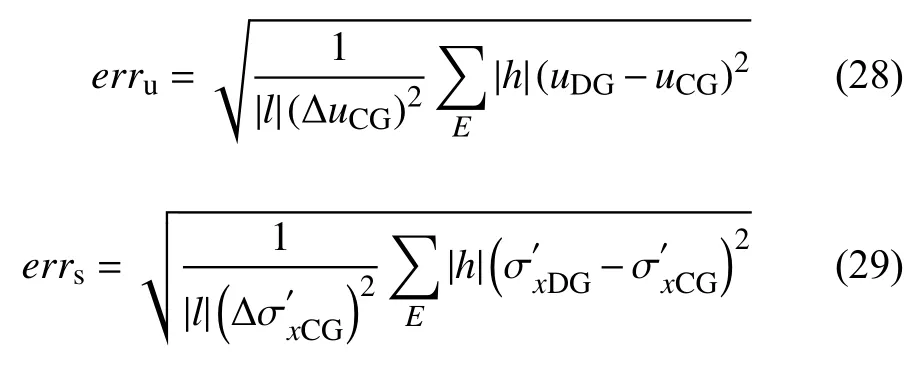
式中,l为几何模型尺度分别为有限元方法计算得到的水平位移和水平有效应力, ΔuCG和分别为间断有限元方法计算得到的水平位移和水平有效应力.

图10 给出了不同加罚因子 δs条件下间断伽辽金有限元和传统有限元方法计算得到的水平位移和水平有效应力的比较.结果表明,随着 δs的增加,间断有限元与传统有限元计算得到的水平方向的变形和应力的相对误差随之减少,这说明了加罚项的增加可以有效抑制有限元函数在跨越单元时的不连续性.

图10 不同加罚因子 δs 条件下间断有限元和传统有限元方法计算水平位移和水平有效应力的比较Fig.10 Comparison of the horizonal displacement and horizonal effective stress between DG and the CG results with different values of penalty parameter δs

3.3 考虑重力效应的两相流固三维算例

在本节中,将开展含水层注氢气的三维数值模拟.在此算例中,侧重分析流体重力效应对模拟结果的的影响.如图11 所示,三维算例的几何尺度为100.00 m×2.00 m×10.00 m.模拟上边界和右边界为应力边界且tx=tz= −1.00 × 107MPa,其余边界均设定为位移约束.氢气从左侧边界注入,注入率gnw=1.00 × 10−4kg/(m2·s),右侧为出口边界,边界上的气体压力和水饱和度分别为4.00 MPa 和0.20,其余边界则为不流动边界.整个注气过程持续1 d,其他变量的数值如表1 所示.

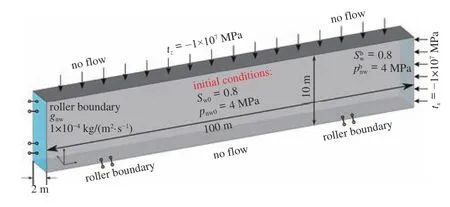
图11 三维模型几何尺度以及模拟初始和边界条件Fig.11 Geometrical configuration with boundary and initial conditions of 3D case

图12 给出了注气1 d 后气体压力pnw、气体饱和度Snw、垂直位移w和水平有效应力的分布云图.图13 为在考虑和不考虑重力效应两种情况下点a,b和c处气饱和度Snw随时间变化图.由图12 可知,氢气注入1 d 后,孔压沿着水平x方向传播至距左边界约70.00 m 处,储层边界处气体饱和度和孔隙压力分别增加至约0.52 和6.50 MPa,孔压的增加引起垂直位移的提高和水平有效应力的降低.在注入过程中,由于氢气和水两者密度的差异,引起气体上浮且聚集于模型顶部,造成顶部点c处气体饱和度要明显高于底部点a处气体饱和度.

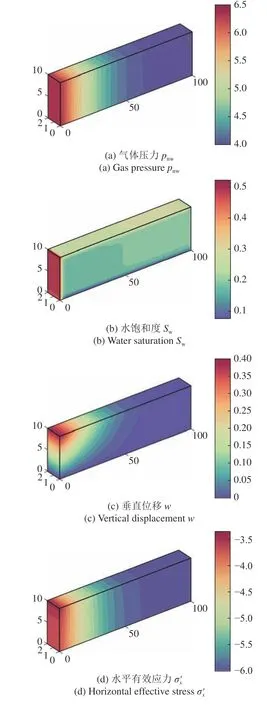
图12 注气1 d 后气体压力 pnw、气体饱和度 Snw、垂直位移 w 和水平有效应力的分布图Fig.12 The distribution of gas pressurepnw,gas saturation Snw ,vertical displacement wand horizontal effective stress after 1 day of injection

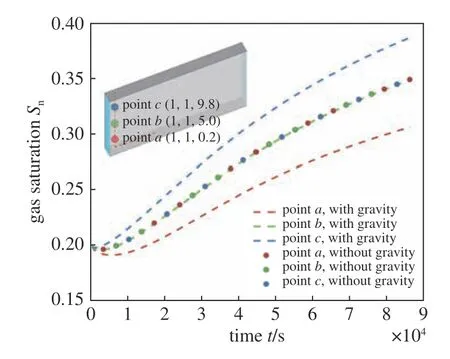
图13 考虑和不考虑重力效应算例中点a,b 和c 处气饱和度 S nw 随时间变化图Fig.13 The temporal evolution of gas saturation S nw at points a,b and c in the cases with and without gravity