白绿色LED 道路光源小目标可见度研究

严晓龙，冯莹莹，李淑敬

（阜阳师范大学 信息工程学院，安徽 阜阳 236041）

1 引言

近年来，我国机动车辆数量逐渐增多，道路交通事故发生率也持续上升，其中由于夜间驾驶光线较暗且可见度较低，夜间事故的发生率远高于白天[1]。加之我国目前大力提倡发展节能照明光源，因此研究夜间行车环境下的道路照明可见度，并在满足可见度的前提下减少照明能源的浪费，以实现夜间驾驶安全、节能之要求有非常必要的现实意义。

当前道路照明可见度的计算，推荐小目标可见度（STV）模型。比如，美国道路照明标准ANSI/IES RP-8-00，提出了基于Adrian 模型的小目标可见度标准，并将其纳入道路光源的设计标准且沿用至今[2]。而目前我国STV 模型的主流研究方法有：何荥等人通过实测阈限亮度数据，基于韦伯费昔勒定律提出能确切反映人眼视看感受的STV算法[3]；翁季、蔡贤云等人对人眼适应亮度和小目标表面/背景亮度等因素进行分析，提出了一种道路照明可见度的简化计算模型[4,5]。但是由于夜间道路照明处在中间视觉条件下（0.001-3.0 cd/m2）[6,7]，而国际照明委员会CIE（Commission Internationale de l′Eclairage）推荐的MOVE 模型等光度学模型无法给出相对固定的人眼视觉函数，且传统阈限亮度差存在计算精度低的问题，间接导致了上述可见度模型的研究算法存在一定误差且计算复杂[8,9]。

本文从反应时间出发，分析中间视觉环境下不同主波长光源的光视光效[10-13]。通过建立的光源主波长和背景亮度关系模型，推导敏感波长、背景亮度和视张角等因素与阈限亮度差的关系。利用敏感波长对阈限亮度差予以修正，提升中间视觉小目标可见度算法的精确度，并通过敏感主波长参数的引入实现光源安全性评价，结合照明功率密度和反应时间对道路照明灯具的节能性进行验证。

2 小目标可见度(STV)模型

目前，STV 模型的可见度常用可见度水平VL 来表示[14]。为了在道路照明灯具设计时方便定量比较，VL 一般取绝对值处理，即：可见度水平绝对值越高，小目标更容易被发现，光源安全性评价越好[15]。如公式（1）所示：

式中，ΔL 为物体亮度和背景亮度差值；ΔL0为阈限亮度差，即目标物可见时阈限亮度与背景亮度差值。ΔL 可以结合实验数据进行计算，运算较为简单，故由上式可知，阈限亮度差才是计算可见度的核心。

RP-8-00 标准基于Adrian 模型给出的ΔL0计算公式得到广泛认可[2]，如公式（2）所示：

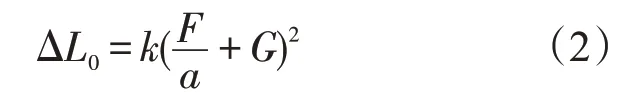
式中，k为感知物体概率因素，F 为光通量函数，α为人眼和小目标物体的视张角，G 为亮度函数。不难看出ΔL0和背景亮度成正比。但是照明背景亮度不建议无节制提高，因为虽然此方法可以提升物体的可见度，但会造成灯具能源的浪费。

众所周知，人眼的视觉功能受锥状、杆状细胞组合影响，这两种细胞使得在中间视觉不同亮度下，人眼对照明光源色彩的敏感程度会有差异，而灯具的配色受主波长的直接影响[16]。因此，研究中间视觉人眼对不同色彩光源（即不同主波长光源）的敏感程度，对评价光源安全性和节能性是非常有效的。

3 基于反应时间的背景亮度/主波长光源模型

现阶段，中间视觉领域的主流观点认为，以驾驶人员发现小目标物体的反应时间为参数，对道路照明光源性能进行评价是最为直观的[17]。因此本节采用较为成熟的行车反应时间测试系统，利用UNITY 3D 平台调节背景亮度和光源波长两大参数值，并在保持视标偏心角等因素不变的前提下，测试驾驶人员对小目标物体的反应时间。通过大量实测数据分析得出：在中间视觉条件下（0.001-3.0 cd/m2），白绿光LED 光源(510-550 nm)人眼反应时间远小于其它配色光源。但是在510-550 nm 波长范围内，选取何种波长值作为该波段色谱的主波长，以保证更好的可见度和节能性需深度研究。核心实验数据如表1：

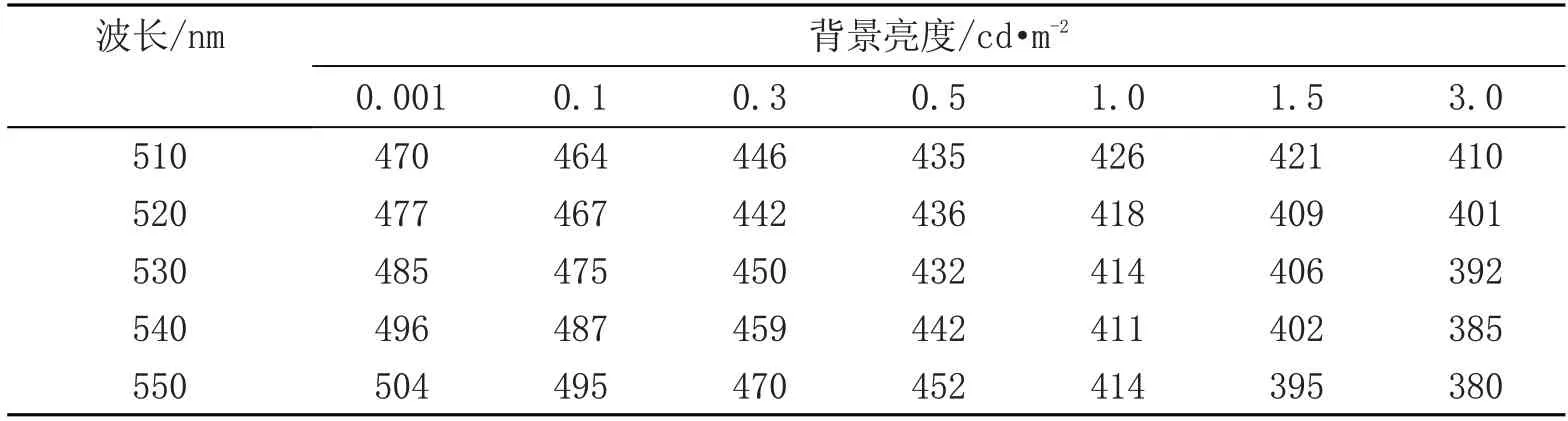
表1 不同波长和背景亮度条件下的反应时间（单位:ms）

由上表可知，中间视觉环境下不同亮度值，均以反应时间最短的波长作为敏感主波长。因此以反应时间为评判标准，得出背景亮度/主波长模型如下：

式中，λm为敏感波长，单位：nm；L 为背景亮度，单位：cd/m2.

该模型对中间视觉条件下的背景亮度和敏感波长进行了公式化表述，利用该模型可以在不同亮度环境下对光源主波长的选取提供理论依据，推导出不同主波长的最优背景亮度值，从而提高道路照明光源效率，避免光源照明亮度过高，保证节能性。基于该模型选取设计的敏感主波长光源，相比其它波长在同等亮度值下光视效能更佳，能充分保障道路行车的安全性。

4 基于背景亮度/主波长模型的可见度修正模型

由于夜间道路照明环境复杂多变，阈限亮度差在进行计算时还需要综合考虑驾驶人员年龄、负对比度和识别时间等影响因素，因此需要在上述关于阈限亮度差计算公式（2）的基础上进行修正，Adrian 和Blackwell 等人建议阈限亮度差修正公式如下[18]：

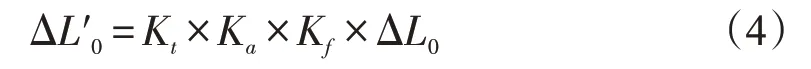
4.1 基于敏感波长的初始阈限亮度差ΔL0

由（2）式可知，传统的初始阈限亮度差计算受光通量函数、人眼视张角和亮度函数影响，其中光通量函数和亮度函数受背景亮度影响，但是仅凭背景亮度无法评价光源节能性。而通过上节背景亮度/主波长光源模型可知，式（3）通过建立敏感主波长和背景亮度的关系，可以保证光源安全性的同时，考虑到节电性能。将（2）式、（3）式联立，用敏感主波长替换光通量函数和亮度函数中的亮度参数，这样既可以对不同主波长光源的可见度进行评价，也可以通过敏感主波长和背景亮度的关系，保证不同波长光源的节能性。将（3）式等价为

将上式和（2）式联立，对ΔL0进行基于敏感主波长的推导：

其中，F 和G的经验公式如下所示：

当Lb≥0.6cd/m2时，

当0.00418cd/m2＜Lb＜0.6cd/m2时，

当Lb≤0.00418cd/m2时，

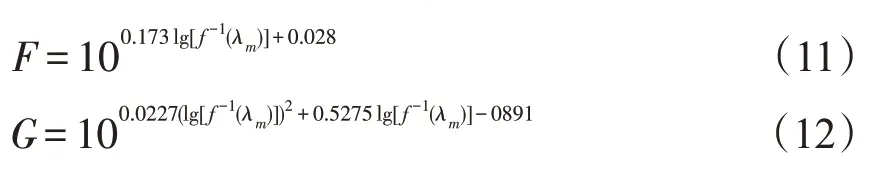
RP-8-00 标准结合对城市道路实测，规定视张角为7.45′[2]，因此代入式（6）-（12）可得波长与初始阈限亮度差ΔL0数据如表2：

表2 波长与初始阈限亮度差关系

4.2 基于敏感波长的负对比修正系数Kf

在日常夜间驾驶的过程中,驾驶人员经常会遇到在明亮的照明背景下观察和发现暗目标，诸如行人、机动车和动物等，这种情况被称之为负对比度，与之相反的就是正对比度。其中式（2）是Adrian 和Blackwell 在正对比度下收集数据并进行的推导[19]，所以需要对该公式进行负对比度修正以满足实际情况，而无需进行正对比度修正。

在不同的中间视觉背景亮度范围下，负对比修正系数Kf也有所区别，结合上节建立的背景亮度/敏感主波长光源模型，对系数Kf 进行基于敏感主波长的推导：

当Lb≥0.1cd/m2时，

当0.003981cd/m2＜Lb＜0.1cd/m2时，

当Lb≤0.003981cd/m2时，

其中，

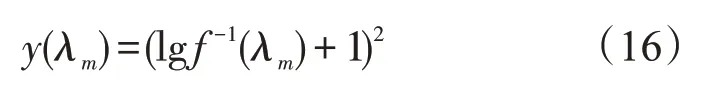
通过计算可得修正系数Kf 与波长关系如表3：

表3 波长与负对比修正系数Kf关系

4.3 基于敏感波长的识别时间修正系数Kt

阈限亮度差在进行计算时，还需要考虑驾驶人员对出现物的识别时间[20]。式（2）建立的初始阈限亮度差模型是基于无时间限制或2 秒的前提下，但是日常夜间驾驶过程中，由于机动车速度以及路况的不同，观察时间往往会比较少，阈值的对比度会随之上升。因此识别时间可以取符合客观情况的0.2s，并用下式进行基于波长的修正：

式中，Kt为识别时间修正系数，g(λm)如式（17）所示。α 为视张角，取7.45′。联立式（17）推导出基于敏感波长的识别时间修正系数Kt，部分数据如表4：

表4 波长与识别时间修正系数Kt关系

4.4年龄修正系数Ka

由于驾驶人员的年龄的不同，人眼的透光率和反应速率也会不同。针对年龄因素，Blackwell和Weale 选取23 岁-75 岁测试者进行视觉实验，并给出年龄修正系数Ka[20]：

由于夜间驾驶环境复杂，驾驶人员年龄上的差异会导致存在较大的视看误差，因此各国标准通常以较大年龄驾驶人员的情况下给出年龄修正系数的建议值。其中RP-8-00 标准推荐识别时间设定0.2s，驾驶员年龄设定60 岁。经式（19）计算可得修正系数Ka 为1.7682。

4.5 基于敏感波长的修正阈限亮度差模型和可见度水平分析

联立波长/初始阈限亮度差关系模型式（6）、修正系数Kf(λm)、Kt(λm)和Ka对ΔL0初始值进行修正，得出基于波长的阈限亮度差修正模型：

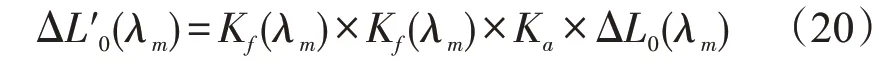
通过该模型，不难得出在中间视觉下的修正阈限亮度差与敏感波长的关系，核心数据如表5所示：

表5 波长与ΔL0′修正阈限亮度差关系

将波长/初始阈限亮度差关系模型式（6）计算的阈限亮度差初始值，和基于波长的阈限亮度差修正模型式（20）计算的修正值进行对比，可以得出关系曲线如图1：

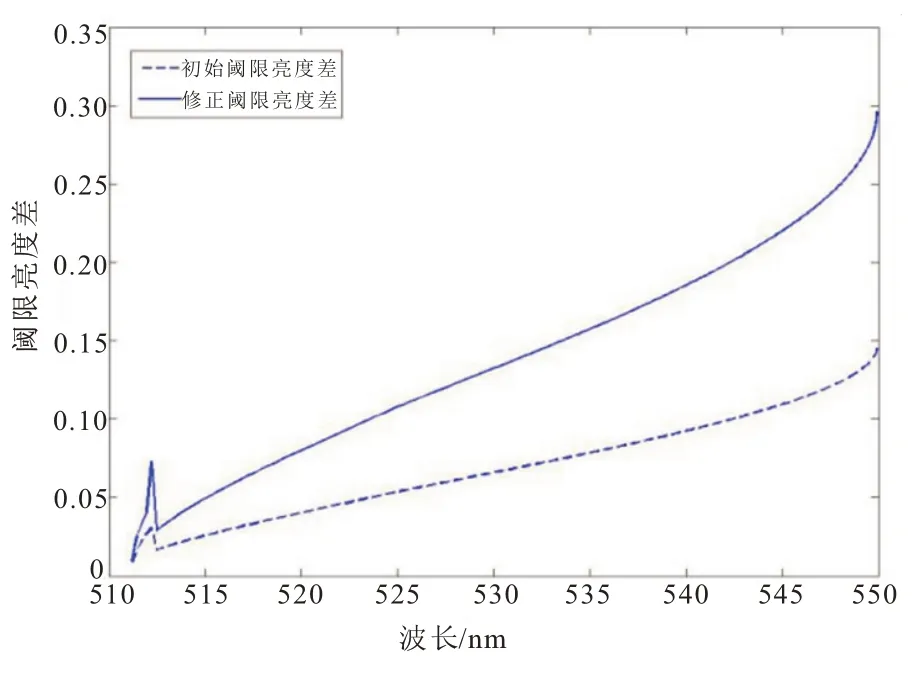
图1 510-550 nm 波长的ΔL0初始值和修正值对比曲线

图1 分析可知，ΔL0修正值比初始值增幅明显。照明光源在510-515 nm 和515-550nm 两个波长范围内，阈限亮度差的初始值和修正值与波长均呈现正比趋势。将该基于波长的阈限亮度差修正模型式（20）与式（1）联立，对可见度水平VL进行计算：

基于式（21）可得波长与小目标可见度水平关系，而RP-8-00 标准给出了在此亮度环境下，识别时间0.2 s、年龄60 岁、视张角7.45′的驾驶视看参数建议值，对比RP-8-00 标准给出的建议值进行验证，核心数据如表6 所示：

表6 主波长与小目标可见度关系

由表6 数据可知，在RP-8-00 提倡的识别时间为0.2 s、驾驶员年龄60 岁、视张角7.45′的机动车道路亮度条件下，当白绿色光源的配色主波长选取528 nm 时，小目标物体的可见度处在最佳水平。

由于实际城市道路环境中，机动车道路面照明亮度水平高于非机动车道，一般处于0.75-3.0 cd/m2。假设小目标物体和背景亮度差恒定-0.5 cd/m2，将本文采用的基于式（21）的可见度算法与上述介绍的何荥等人建立的基于韦伯—费昔勒定律的可见度水平算法、翁季等人提出的道路照明可见度简化模型，带入不同机动车道路面照明亮度环境进行对比，得出与RP-8-00 推荐值的相对误差如表7 所示：

表7 不同亮度下三种可见度算法与RP-8-00的相对误差比较

由表7 可以看出，本文提出的基于式（21）的可见度模型算法误差明显更小，因此该模型是非常可靠的，可以将其应用在复杂多变的中间视觉夜间驾驶条件中。

5 实验测试与分析

基于上节结论，利用TRACE PRO 对白绿色LED 灯具（510-550 nm）进行基于528 nm 主波长的光谱设计，并将设计灯具与金卤灯、高压钠灯等其它传统灯具带入DIALUX 软件进行照明仿真实验。其中，实验环境参数如下：道路参数设置为RP-8-00 建议的机动车道路中间视觉背景亮度范围（0.75-3.0 cd/m2），道路照明灯具间隔15 m，灯具高度8 m，道路宽度为14 m；三种对比灯具的额定功率统一选取132 W。经DIALUX 软件仿真后，三种灯具在机动车道上的亮度等线图如图2 所示：

图2 在三种灯具照明下的道路亮度等线图(a)白绿色LED 灯具；(b)高压钠灯；(c)金卤灯

根据图2 亮度数据进行道路平均亮度计算，数据如表8 所示：

表8 三种灯具照明下的道路平均亮度值

由表8 可知，528 nm 白绿色LED 灯具照明下的道路平均亮度最高，高压钠灯其次，金卤灯最低。通过DIALUX 进行亮度仿真模拟，伪色图结果如图3 所示：

图3 在三种灯具照明下的道路伪色图(a)白绿色LED 灯具；(b)高压钠灯；(c)金卤灯

结合道路平均亮度和伪色图分析不难得出，528 nm 白绿色LED 灯具对道路的亮度提升非常明显，也间接验证了当白绿色光源的配色主波长选取528 nm 时，道路的可见度处在最佳水平的结论。

此外，将528 nm 白绿色LED 光源与金卤灯、高压钠灯进行同等道路条件下的反应时间测试实验对比，结果表明：相比传统配色光源，528 nm 白绿色LED 光源反应时间更短，传统光源若想达到同等反应时间水平，必须增加灯具发光亮度，导致灯具能耗增加，实测数据如表9 所示。

表9 机动车道路亮度下不同灯具的反应时间实测数据（单位:ms）

6 结论

本文研究了中间视觉环境下基于波长的阈限亮度差模型，并基于此模型对不同主波长的白绿色LED 光源的小目标可见度进行评价。

（1）基于大量实测数据拟合的背景亮度/敏感波长关系模型，对不同主波长白绿色光源（510-550 nm）在中间视觉条件下的初始阈限亮度差进行评价。利用波长参数对初始阈限亮度差进行合理修正，并最终给出了一种基于波长的中间视觉阈限亮度差的修正模型。

（2）通过对阈限亮度差进行基于波长的推导修正，将其带入小目标可见度模型，可以直观给出不同敏感主波长LED 灯具的可见度水平，进而建立了波长/可见度水平模型，经验证精确性较高。通过该模型可以对不同波长的配光灯具进行对比，并得出在RP-8-00 提倡的识别时间为0.2 s、驾驶员年龄60 岁、视张角7.45′的机动车道路亮度条件下，白绿色LED 光源以528 nm 作为主波长进行色谱设计，相比传统配色光源安全性更好。这为今后道路照明灯具在进行安全性方面考虑时，提供了有效依据和参考。