群决策共识过程的优化及其在农产品滞销中的应用①

胡文文， 金飞飞， 郑晓涵， 李盈盈， 孟繁熙

(安徽大学商学院，安徽 合肥 230601)

0 引 言

在面临重大事件时，一个人往往不能做出准确的决策，取而代之的是群组决策。目前，群决策被认为是一种快速做出最优决策的高效准确的手段，越来越多的专家投入更多的时间和精力深入研究群决策[1,2]。在进行决策之前，专家们需针对不同的方案发表自己的看法。为了解决难以使用具体的数值来衡量方案好坏的问题，部分专家提出使用模糊语言比较方案的优劣。然而，在实际决策时，单一的语言变量很难准确地表达出专家们的真实想法。因此，部分学者使用犹豫模糊语言偏好关系[3,4]表达专家们的观点。

群决策是综合多位专家的意见达成共识，最后对方案进行排序并做出最优决策的过程。如何使专家们的意见达到统一是当前研究的热点问题。张金波[5]和姜乐[6]两位学者都基于犹豫模糊语言采用多属性决策方法，以使专家们的意见达成共识；Zhang等[7]基于概率语言偏好关系利用距离测度和改进算法不断衡量与调整做出最优决策；Xie等[8]基于概率不确定性语言偏好关系利用距离测度和相似度衡量专家们观点的共识性。综合考虑专家们评价时的犹豫性以及决策效率，基于犹豫模糊语言偏好关系利用距离测度和相似度衡量专家们观点间的差距，并提出一种新的改进算法提高专家们的共识性，最终完成整个决策过程。

1 预备知识

语言术语集有助于专家使用定性语言变量进行方案间的两两比较，解决了一些无法用精确数据描述的问题，因此在决策分析方面得到了广泛的应用。

令S={sα|α=0,1,2,…,2τ}为一个语言术语集(Linguistic Term Sets, LTS)[9]，则该LTS满足下列性质[10]：

(1)有序性：α>β⟺Sα>Sβ.

(2)逆算子：Neg(Sα)=S2τ-α(α=0,1,2,…,2τ).

(1)Sα⊕Sβ=Sβ⊕Sα=Sα+β,

(2)λSα=Sλα,

(3)(λ1+λ2)Sα=λ1Sα⊕λ2Sα,

(4)(Sα⊕Sβ)⊕Sγ=Sα⊕(Sβ⊕Sγ).

其中，Sα是S的一个语言变量，设I(Sα)为下标函数，即I(Sα)=α。

定义1[12]：假设X={x1,x2,…xn}为一个有限方案集，基于语言术语集定义在方案集X上的矩阵H=(hij)n×n⊂X×X称为犹豫模糊语言偏好关系(HFLPR)。

其中，hij为一个犹豫模糊语言元(HFLE)，hij∈S={s0,s1,…,s2τ}，其表示方案xi相对于方案xj的语言偏好程度。

为了计算方便，假设除了偏好关系对角线上的犹豫模糊语言元外，其余所有的犹豫模糊语言元所包含的语言变量数量都相等，且按升序排列。

2 基于HFLPR的共识性测度

专家们对方案间的两两评估具有一定的主观性。因此，可以利用以下部分介绍的共识性测度方法衡量专家们的意见是否达成共识。

定义3设Hm=(hij,m)n×n为第m个专家做出的HFLPR，hij,p,hij,q为定义在S上的HFLE，

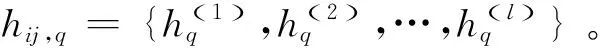
(1)

则称d(hij,p,hij,q)为hij,p和hij,q的距离测度。

性质1：0≤d(hij,p,hij,q)≤1

性质2：d(hij,p,hij,q)=d(hij,q,hij,p)

性质3：d(hij,p,hij,q)+d(hij,q,hij,r)≥d(hij,p,hij,r)

定义4设Hp和Hq分别是专家ep和eq提供的犹豫模糊语言偏好关系，根据HFLE间的距离测度d，可以利用以下公式计算HFLPR间的距离测度。

(2)

相似度[13]

s(Hp,Hq)=1-d(Hp,Hq)=

(3)

3 群共识性指数改进算法与群决策模型的构建

3.1 群共识性指数的改进算法

通常情况下，由于专家们在对方案进行评价时带有一定的主观性，专家们的意见很难达成一致。基于此，需要从多方面综合考虑，对专家的想法进行修改与调整，以提高专家决策的共识性，最终使专家们的意见达成共识。

定义5令H1,H2,…Hm为m个HFLPR,那么关于Hk(k=1,2,3,…,m)的群共识性指数定义如下：

(4)

(5)

根据以上过程，群共识性指数的改进算法如下所示：

算法一

输入：m个HFLPRH1,H2,…Hm，群共识性指数GCI的阈值δ0。

Step 1 利用公式(1)计算HFLE间的距离，得到d(hij,p,hij,q)。

Step 2 利用公式(2)计算HFLPR间的距离，得到d(Hp,Hq)。

Step 3 利用公式(4)计算群共识性指数GCI。

Step 4 共识性检验。根据事前给定的共识性指数阈值δ0，判断群共识性指数是否可以接受。若GCI≥δ0，则进入到步骤8；否则，继续进行下一步。

Step 5 通过两两比较，筛选出距离测度最大的两位专家Hp,Hq。在此基础上，筛选出距离测度最大的HFLEhij,p,hij,q。

Step 6 综合考虑这两位专家的权重，若ωp>ωq，则利用公式(5)调整专家q的HFLPR；反之，则利用公式(5)调整专家p的HFLPR。

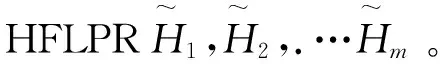
Step 8 结束

(6)

(7)

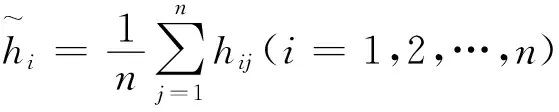
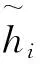
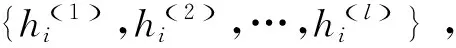
(8)

3.2 基于HFLPR的群决策模型

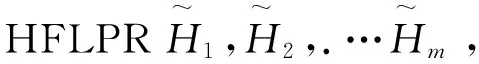
Stage 3. 挑选出最优方案。利用得分函数(8)评估每个方案的属性值，并对其进行排序。

4 模型应用

4.1 算例分析

通过调查可知，近年来，农产品滞销现象仍频频发生。例如，2019年12月，赣州宁都县面临着近80万斤的赣南脐橙滞销。2020年初受疫情的影响，我国多地均出现滞销现象。据新闻报道，云南宜良县存在蔬菜滞销现象，滞销品种多达10多个品种。此外，海南的菠萝、芒果等水果也面临着滞销的风险。虽然目前我国已处于电商快速发展的时代，但由于部分农产品种植规模大且保质期短，电商也无济于事。在2019年的八月中旬，宁夏中卫市出现大量中卫西瓜滞销现象。上述这些农产品滞销现象只是大量新闻报道中的几个典型事件，而且真实发生的滞销事件远高于新闻报道的数量。农产品滞销不仅使农民的经济受到巨大损失，而且对整个农产品市场供应造成一定的影响。导致这些问题产生的部分原因是决策者不能针对农产品滞销现象做出快速有效地分析并及时采取相应的应对措施和手段。假设目前某地区发生了一场农产品滞销事件，通过调查可知，农产品滞销主要有以下四个原因，x1盲目扩大生产，x2产品缺乏竞争力，x3市场供应饱和，x4产销信息不对称。此外，有三位专家em(m=1,2,3)组成一个专家讨论小组，共同为此次农产品滞销事件进行决策，三位专家的群众分别为ω=(0.2,0.5,0.3)T。现有一个LTSS={s0:特别差,s1:很差,s2:一般,s3:稍微差,s4:一般,s5:稍微好,s6:好,s7:很好,s8:特别好}，专家们基于该语言术语集做出的HFLPR如下[11]：

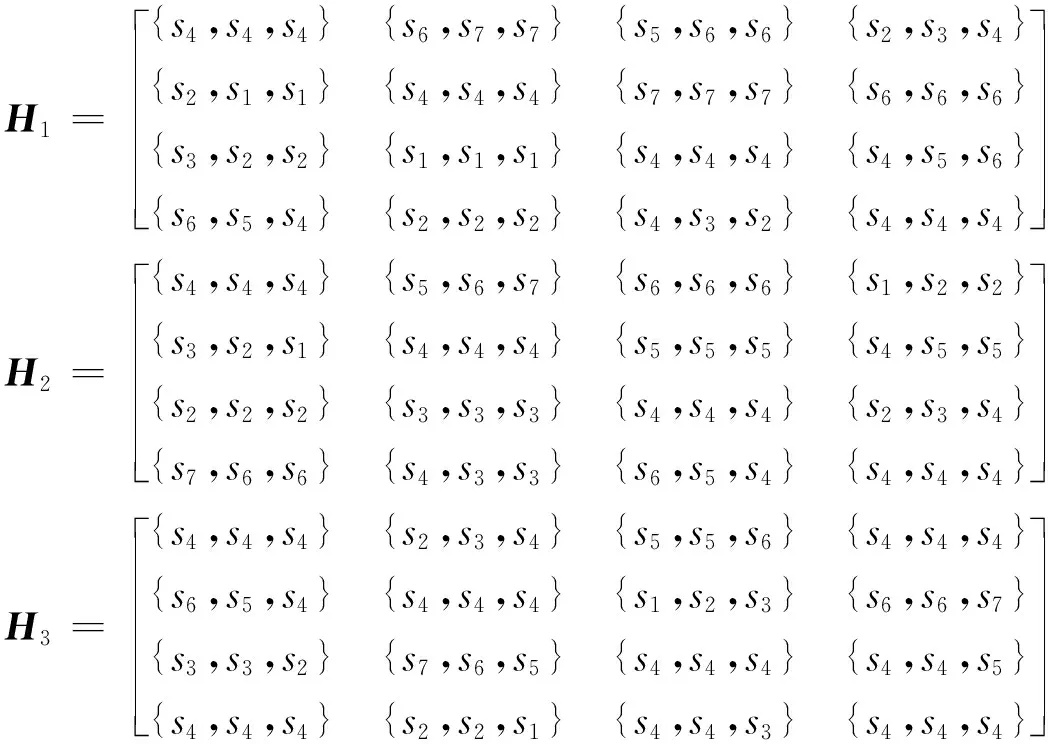
首先，根据公式(1)和公式(2)计算得到

d(H1,H2)=0.1978，d(H1,H3)=0.2893，

d(H1,H2)=0.2996

接着，根据公式(4)计算得到GCI=0.7378。令共识性指数δ0=0.9，通过比较可得，GCI=0.7378<δ0，因此，需要对专家所做出的HFLPR进行调整。

根据公式(5)，得到调整后的HFLPR，如下所示：

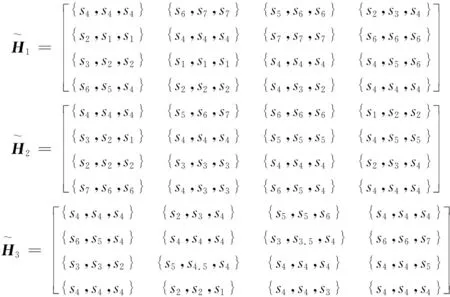
重复以上步骤，计算出GCI=0.7626<δ0，根据算法一，多次循环运算，得到最终调整好的HFLPR，如下所示：

根据调整好的HFLPR计算得到GCI=0.9011>δ0。

最后，根据公式(6)，利用HFLWA算子将其整合为一个HFLPR

接着，利用公式(7)计算，得到：

通过公式(8)，利用得分函数得到：

因此，通过比较可以得到四种原因的排序结果：x1>x4>x2>x3。所以，该农产品滞销事件最可能的原因是x1盲目扩大生产。

4.2 对比分析

为了证明该模型的合理性和准确性，将该模型和文献[11]的决策结果相比，所构造的共识模型运行出的结果与文献[11]相同，均为x1>x4>x2>x3，说明该模型具有一定的可行性和合理性。

经过对比发现，该模型与文献[11]的模型主要在以下三方面有所不同：

(1)共识性指数。对专家们的HFLPR进行两两比较并计算距离测度，在此基础上计算群共识性指数进行比较；而文献[11]需要反复计算整合的HFLPR，基于此计算每个专家的HFLPR的共识性指数并进行比较。

(2)改进HFLPR的方法。通过比较专家们意见间的距离测度和衡量调整成本，有针对性地修改特定专家特定位置上的语言变量；而文献[11]在比较个体HFLPR共识性指数后将对所有专家的HFLPR进行修改。

(3)参数的设定。需要提前设定的参数较少，即共识性指数阈值；而文献[11]所涉及的参数较多，例如共识性指数阈值、调整控制参数等。

综上所述，和文献[11]相比，构建的共识模型的特点为在偏好关系上，更能保留数据的原始状态；在提高共识性算法上更具有直接性、针对性。

5 结 语

基于犹豫模糊语言偏好关系构建了共识模型，从而解决群决策问题。首先，介绍了关于犹豫模糊语言偏好关系的基本概念。其次，针对专家们所做出的犹豫模糊语言偏好关系，利用共识性测度衡量专家们意见的共识性。再次，为了使专家们的意见达成共识，综合考虑专家们观点的调整成本，对专家们的意见做出调整。最后，利用犹豫模糊语言加权平均算子整合所有调整好的HFLPR，再计算得分函数进行比较，找到最佳方案。通过案例分析和对比分析得出，提出的决策过程具有合理性和有效性。