融合互补滤波和卡尔曼滤波的姿态解算算法

刘 颖，杨 媛，徐金涛

(1.西安邮电大学 自动化学院，陕西 西安 710121；2.中国科学院西安光学精密机械研究所 西安中科华芯测控有限公司，陕西 西安 710119)

随着现代化微电子和微加工技术的发展，由微电子机械系统(Micro-Electro-Mechanical System，MEMS)陀螺仪、加速度计和地磁计组成的捷联惯性测量单元作为惯性导航系统重要的组成部分，已广泛应用在航空航天、军事等领域。在惯性导航系统中，姿态角的测量和解算是重要的控制部分[1]，只有得到较为准确的姿态信息，才能对测量对象的运动姿态进行控制，因此，提高载体姿态解算精度一直是研究热点。在实际对姿态进行解算过程中，MEMS陀螺仪在进行积分运算时会产生累计误差，并且受工作温度的影响会产生温度漂移。加速度计在静态实验中，可以得到相对稳定且准确地数据，但是在动态试验中，容易受到外界环境以及噪声影响，进而影响数据的采集。地磁计所采集的数据在实验过程中可能会受地磁等因素的影响。因此，通常融合3个传感器数据进行姿态解算[2]。

目前，已有多种传感器数据融合的姿态解算方法。较为成熟的有互补滤波技术、卡尔曼滤波技术、粒子滤波技术和神经网络技术等。其中，互补滤波原理较其他方法简单，运算量较小，主要适用于姿态精度要求较低的惯性导航系统，能够对噪声和漂移进行抑制，但其截止频率不易确定，并且如果惯性系统对姿态解算精度有较高要求或者惯性系统长期处在运动状态，单纯使用互补滤波对姿态进行解算往往是不能满足预期的要求。除此之外，卡尔曼滤波也被广泛的应用于姿态解算。卡尔曼滤波算法[3]的实时性强，且结构简单，但是不适用于非线性系统。在此基础上，扩展卡尔曼滤波[4]被提出，其主要工作是将状态方程和量测方程进行线性化处理，对于弱非线性系统，可以获得较为准确的结果，而对于强非线性系统，则会导致滤波器性能下降甚至滤波发散，从而产生误差。文献[5]提出了一种改进的自适应卡尔曼滤波算法，利用预报残差的方法求解最佳遗忘因子，进一步对在线估计的量测噪声协方差阵和状态估计误差方阵采用上三角-对角(Unit Upper Triangular and Diagonal Factorization，UD)分解的形式进行表示和更新，以此避免自适应滤波过程中的滤波发散现象。

在文献[5]的基础上，拟提出一种基于互补滤波和改进自适应卡尔曼的姿态解算融合算法。利用互补滤波器融合多个传感器数据信息以提高测量精度，并将融合得到的姿态信息作为观测值，通过改进的自适应卡尔曼滤波器，弥补在动态环境下滤波过程中存在的发散问题，以期得到精确的动态情景下的姿态解算信息。

1 载体姿态描述与更新

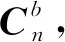
(1)

式中：θ、ψ和φ分别表示绕坐标轴yb转过的角度、绕坐标轴zb转过的角度以及绕坐标轴xb转过的角度；q0、q1、q2和q3表示当前时刻的四元数参数值。

姿态更新理论是基于MEMS陀螺仪、加速度计以及电子罗盘组件的测量值对姿态矩阵进行实时更新，采用四元数法进行更新姿态数据。在具体的实践中，四元数可描述刚体对于某个坐标系的定点运动，表达式中标量部分表示刚体转动角余弦值的一半，矢量部分分别表示刚体转动角度、旋转轴以及转动方向，即

(2)

式中：θ为转动角度；旋转轴的旋转方向为uR，R表示坐标系。将求解得到的四元数代入式(1)可以得到

(3)

2 互补滤波

在俯仰角和橫滚角的测量上，加速度计的静态响应较好，但是在动态环境下会存在不可消除的动态噪声，从而降低姿态解算精度。一般利用磁力计求解航向角，但同样低频段响应较好，高频段响应存在明显缺陷。对于MEMS陀螺仪来说，在动态环境下仍有较好的性能，但在处理陀螺数据时需要进行积分运算，会产生累积误差，故需要设计一个低通滤波器解决短时间内快速变化的噪声，保留有效信号。同时，还需要一个高通滤波器对累积误差进行处理。因此，结合两种滤波器的特点设计互补滤波器以提高解算精度[7]。利用加速度计和MEMS陀螺仪在各频率段的特性，设计由一个低通滤波器和一个高通滤波器组成的互补滤波器，频率互补，其原理如图1所示。

图1 互补滤波原理

图1中，低通滤波器和高通滤波器的传递函数满足如下关系[8]

(4)

式中：G1(S)和G2(S)分别表示低通滤波器和高通滤波器的传递函数；S表示在频域分析中以虚指数为基本信号；K1表示低通滤波器调整权值；K2表示高通滤波器调整权值。

加速度计和电子罗盘得到的姿态信息包含高频噪声，而MEMS陀螺仪的输出值包含低频噪声。传感器1是由加速度计和磁力计组成得到的姿态信息，包括航向角、俯仰角和橫滚角，用C1(S)表示，传感器2是MEMS陀螺仪测量的姿态角，用C2(S)表示，则真实的姿态信息C3(S)与C1(S)和C2(S)的关系可表示为

(5)

式中，ε1和ε2表示噪声对姿态信息的影响。

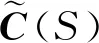
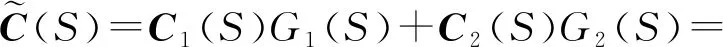
(6)

事实上，互补滤波器中K1和K2的确定直接影响了最终姿态角的确定。当K1和K2越小，加速度计和磁力计测量姿态信息过程中的高频噪声就能很好地抑制，但是不能有效抑制陀螺仪在计算过程中所产生的积分误差。当K1和K2过大时，对陀螺仪产生的累积误差有很好的抑制效果，但姿态角随着加速度计和磁力计的解算速度加快噪声也会越来越大。

利用差分法得到时域姿态解算公式为

(7)

3 改进自适应卡尔曼滤波

经典的卡尔曼滤波仅适用于已知噪声的先验统计特性的线性控制系统，即系统阶数已知的情况。然而，在实际应用中，滤波的先验性值往往很难确定或者是随时间不断变化，对于运动模型的系统噪声Q和测量噪声R的获取十分困难，具有时变性和不确定性，故在复杂情况下经典卡尔曼滤波不能发挥其作用[9]。因此，能够自动控制的改进自适应卡尔曼滤波算法可改善先验信息不足、模型不够精确等问题。

Sage-Husa自适应卡尔曼滤波算法的实质是当系统的噪声协方差矩阵Q和观测噪声协方差阵R不确定时，滤波器自身可利用测量数据所得出的信息不断地对系统噪声特性以及滤波器的增益矩阵进行估计和修正，也就是在离散卡尔曼的基础上，计算k时刻的系统干扰均值qk、系统干扰协方差矩阵Qk、量测噪声均值rk和量测噪声协方差矩阵Rk，并进行调整，从而减少滤波过程中的估计误差，进一步提高滤波精度[10]。

状态预测表示为

(8)

预测误差表示为

(9)

滤波增益表示为

(10)

新息估计表示为

(11)

状态估计表示为

Xk=Xk|k-1+Kkεk

(12)

误差估计表示为

Pk=(I-KkHk)Pk|k-1

(13)

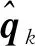
(14)

(15)

(16)

(17)

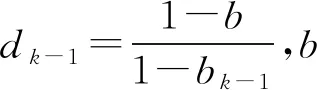
在Sage-Husa自适应卡尔曼滤波算法中，bk-1的选择关系到滤波是否发散，会直接影响最终滤波的精度。为此，需要制定一个检验标准判断滤波是否发散[11]，即

(18)

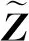
(19)

又因为有以下关系

(20)

将式(20)代入式(19)，可得最佳遗忘因子为

(21)

遗忘因子可对滤波器的记忆长度进行有效的限制，使新获得数据在估计中发挥作用，从而加强新观测数据在实时估计中的作用，同时加速对陈旧数据的遗忘，使其在实时估计中发挥较少的作用[12]。UD分解Sage-Husa自适应滤波是一种可以提高滤波数值稳定性的有效分解滤波的方法。由于UD分解Sage-Husa自适应滤波在实际操作过程中运算量更少，故可在实际场合进行应用[13]。

由于Pk、Pk|k-1容易出现负定的情况，因此先对Pk、Pk|k-1进行UD分解，得到

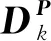
(22)

令矩阵

则式(22)可以表示为

(23)

(24)

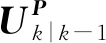
(25)

利用上述方法对Pk-1和Pk进行UD分解，得Pk|k-1的UD分解表达式为

(26)

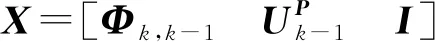
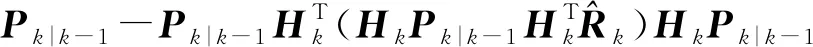
(27)

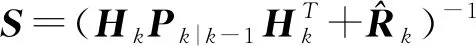
再进行UD分解，得到关系式

(28)

通过式(28)得到Pk的UD分解，令

代入式(28)，并对V进行UD分解，得到关系式

(29)

从而得到了Pk的UD分解更新表达式为

(30)

4 融合算法

通过四元数法可以求解并表示空间中的载体姿态，如横滚角、航向角及横滚角信息等，但仍然会存在制造工艺、环境温度以及积分过程中存在的累计积分误差等问题。为了提高姿态解算的精度，将互补滤波和改进自适应卡尔曼姿态解算算法进行融合，进一步提高姿态解算精度。在自适应卡尔曼滤的递推步骤中，利用UD分解避免了计算过程中出现负定的情况，抑制了滤波发散。在实际的应用中，利用改进自适应卡尔曼滤波进行姿态解算更新前需要输入观测值。在对观测值进行测量时，利用互补滤波器进行数据融合，避免加速度计和电子罗盘在动态、高频率情况下的噪声影响，将最终得到姿态角带入四元数微分方程和更加精确的四元数，从而得到更加精确的姿态角[15]。基于互补滤波和改进自适应卡尔曼的姿态解算融合算法进行姿态解算过程如图2所示。

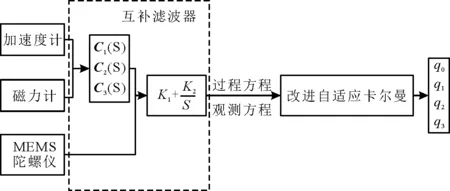
图2 融合算法姿态解算过程

5 实验及结果分析

采用型号为HX-INS-12的MEMS惯性测量单元进行跑车实验。基准采用一个高精度激光惯导系统，姿态角数据更新周期为30 ms，航向角精度0.04°，姿态精度0.01°，对准时间不超过6 min，MEMS陀螺仪的零偏值为10°/h，加速度计的零偏值为15 mg。将高精度激光惯导系统和电子罗盘固定在车辆中，连接好天线等其他设备。车辆开动后，进行40 min的数据采集，得到三轴陀螺的数据、三轴加速度传感器的数据以及磁力计的数据，将数据通过互补滤波器得到互补滤波的观测值，最后通过改进自适应卡尔曼滤波得到最终精确的偏航角、俯仰角和横滚角。

分别利用互补滤波算法、改进自适应卡尔曼滤波和所提融合算法对采集到的数据进行姿态解算。在600 s内，利用上述3种算法得到的横滚角、俯仰角和航向角分别如图3、图4和图5所示。

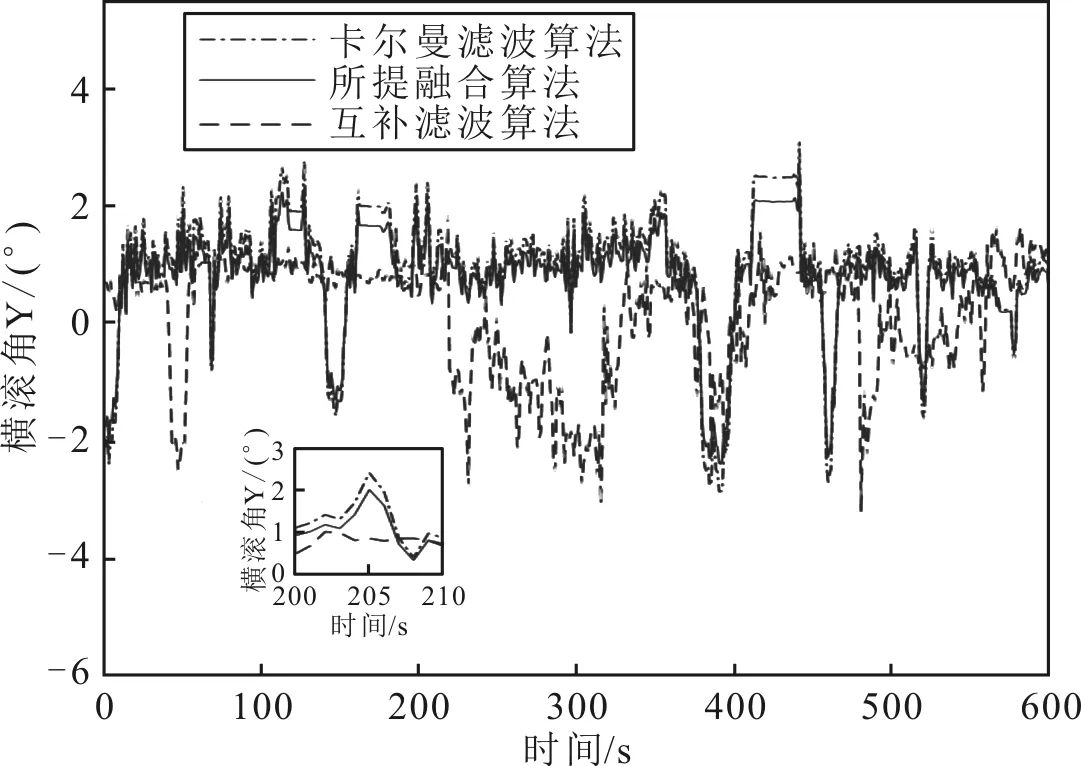
图3 横滚角

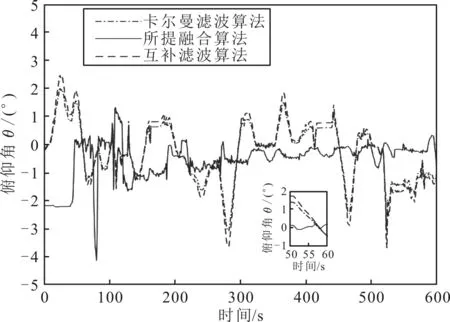
图4 俯仰角

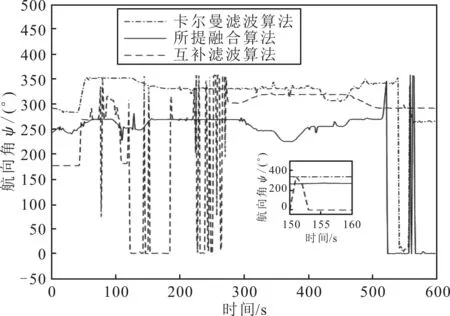
图5 航向角

对比分析3种算法解算得到的横滚角、俯仰角以及航向角与实际横滚角、俯仰角和航向角，误差对比曲线分别如图6、图7和图8所示。

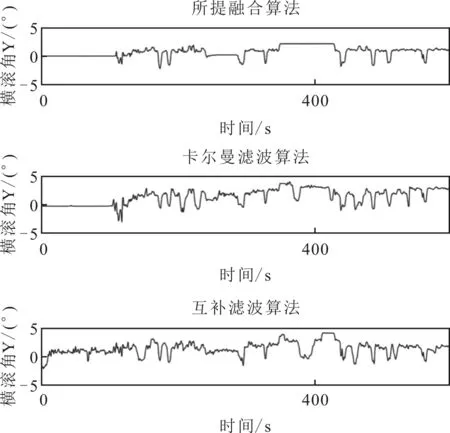
图6 横滚角误差曲线

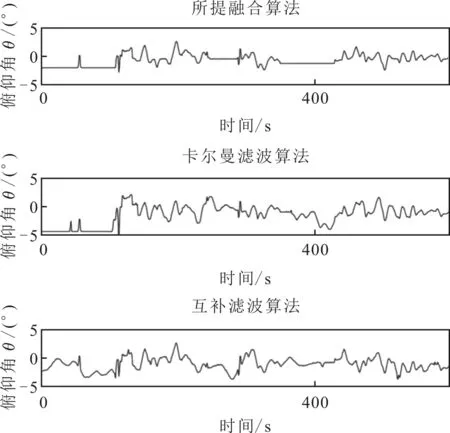
图7 俯仰角误差曲线

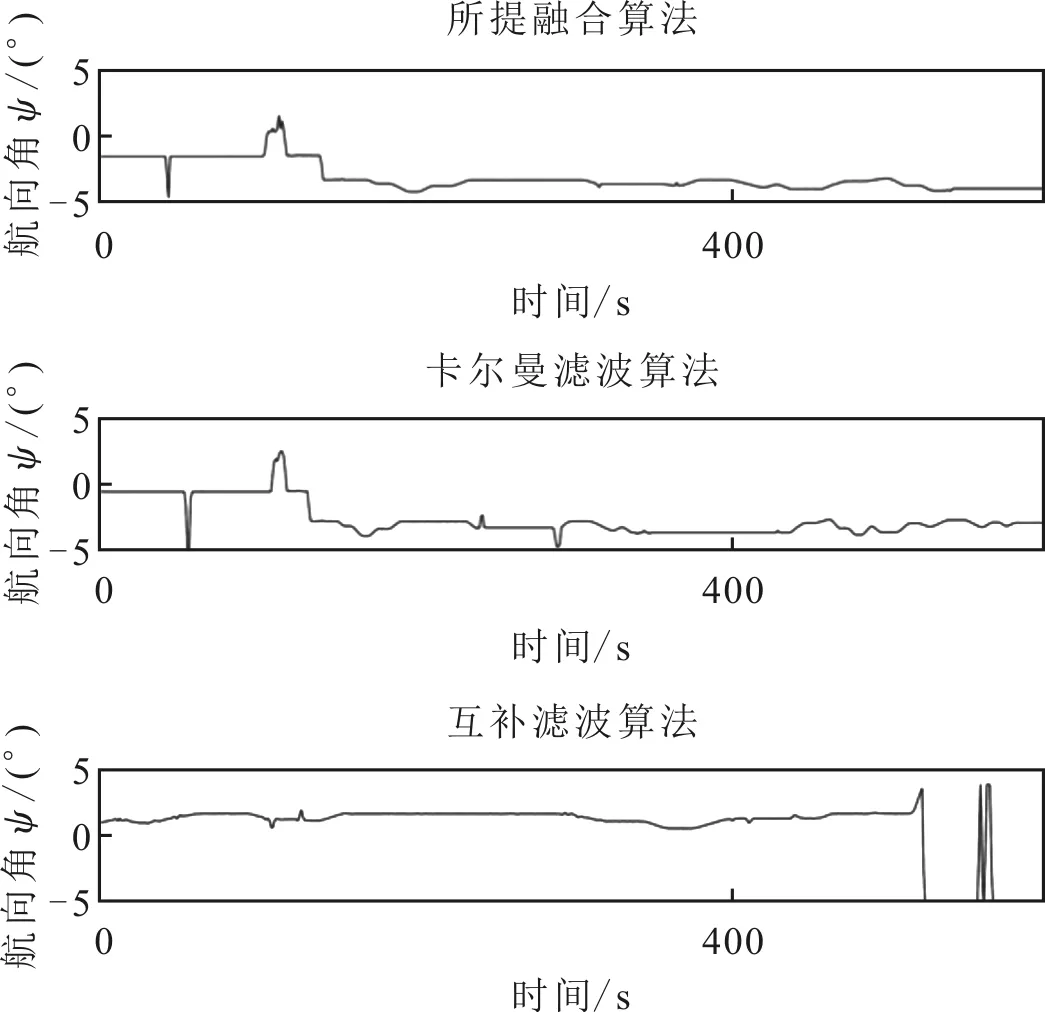
图8 航向角误差曲线

从图6—图8中可以看出，利用所提融合算法、互补滤波算法以及改进自适应卡尔曼滤波进行姿态解算，得到的横滚角误差分别为2.2°、2.7°和3.5°，俯仰角误差分别为1.8°、2.5°和3.7°，航向角误差分别为1.7°、2.7°、3.4°。较互补滤波算法和改进自适应卡尔曼滤波算法，所提融合算法在横滚角误差上分别降低了18.5%和37.1%，在俯仰角误差上分别降低了28.0%和51.4%，在航向角误差上分别降低了37.0%和50.0%。

6 结语

基于互补滤波和改进自适应卡尔曼的姿态解算融合算法，通过低通滤波器和高通滤波器相结合的方法，对短时间内快速变化的噪声进行过滤，并对累积误差进行处理。改进自适应卡尔曼滤波算法是在传统的Sage-Husa自适应卡尔曼滤波的基础之上与UD分解进行结合，保障了量测噪声、预测误差协方差阵以及状态估计协方差矩阵的正定性，对滤波发散具有明显的抑制作用。实验结果表明，互补滤波算法和改进自适应卡尔曼滤波算法的姿态角解算精度低，且收敛速度较慢，在动态实验中还容易出现发散的情况，而所提融合算法结构较为简单，收敛速度快，能够有效抑制滤波发散，保证较高的姿态解算精度。