基于VOF方法的稳压器用单螺旋喷雾头性能优化

2021-11-10王宇阳余纪成

科技视界 2021年30期

刘威成翔王宇阳余纪成苏桐

（中国核动力研究设计院核反应堆系统设计技术重点实验室，四川成都610041）

0 引言

在压水堆一回路系统中，稳压器喷雾头位于稳压器内部蒸汽空间，通过喷射雾化的过冷水，抵偿、衰减系统压力正波动，它的雾化性能直接决定了其缓解系统压力正波动的能力。稳压器喷雾头通常在较小的驱动压差（0.2 MPa左右）下工作，具有低压差、大流量的特点，一般采用离心式喷雾头，常见形式有螺旋式与叶片式。

以往对喷雾头雾化特性的研究主要建立在经验和试验的基础上，由于雾化过程的复杂性，目前雾化理论研究尚不成熟，无法直接用于各种类型喷雾头雾化特性的理论计算。离心式喷嘴也常用在火箭发动机、燃气轮机等设备中，随着近代流体力学的发展，该领域的学者利用两相流数值计算方法对离心式喷嘴进行了更为深入的研究，其中，两相界面追踪流体体积（Volume of Fluid，VOF）方法应用最广，常被用于模拟喷嘴射流破碎及预测喷嘴雾化锥角等[1-6]。

为设计一种冷态额定流量30 t/h的稳压器大流量单螺旋式喷雾头（结构形式见图1），在开展相应的冷态试验前，需对设计的喷雾头进行性能预测以评价设计合理性。因此，本文利用VOF方法，在验证数值方法及模型适用性的基础上，研究关键结构参数对进出口压降、喷雾锥角、喷雾均匀度的影响，最终确定合适的结构参数。

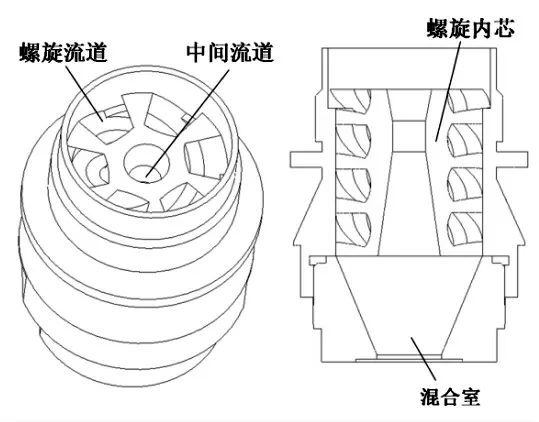
图1 单螺旋式喷雾头

1 数值方法及试验验证

对前期设计的小流量单螺旋喷雾头进行数值模拟，并利用已有试验数据对数值计算方法进行验证。由于数值模拟较难精确模拟喷雾水的破碎雾化过程，因此仅通过对喷雾头内部流动及靠近喷嘴的有限外流场区域中的射流行为进行模拟，来预测喷雾头的有关性能。

1.1 数值方法

1.1.1 数学模型

在两相流模型中，目前最为完善可靠的模型是两流体模型，其中VOF模型最为适合模拟流体射流破碎和追踪气液交界面[7]。湍流模型选用RNG k-模型，该模型可以更好地处理高应变率及流线弯曲程度较大的流动。

1.1.2 网格模型及边界条件

图2给出了喷雾头的计算网格模型。取空气为第一相，水为第二相。入口采用速度入口，给定入口流量，水体积分数设置为1。出口为外流场域边界，采用Opening边界条件，相对压力为0 MPa，水的体积分数设置为0。壁面条件设置为无滑移粗糙壁面。

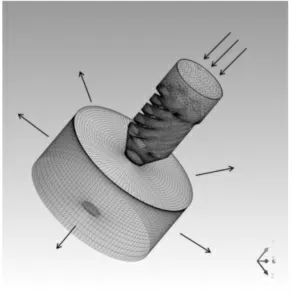
图2 喷雾头网格模型及边界设置

1.1.3 典型计算结果分析

图3给出了喷雾头剖面上的压力分布云图，额定流量下进出口压降计算值为0.241 MPa。

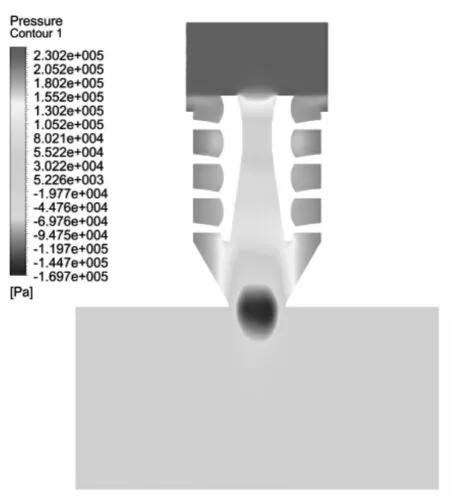
图3 喷雾头剖面压力云图

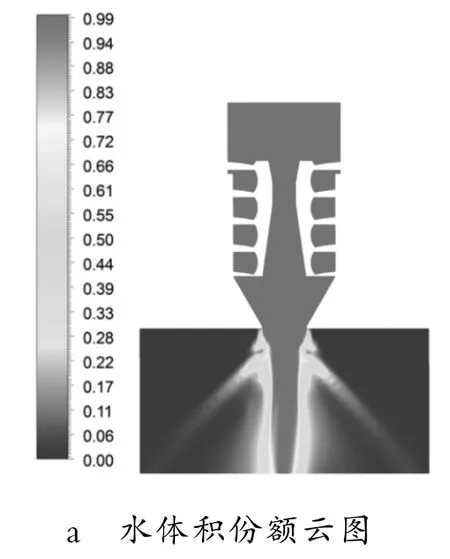
图4 a给出了剖面上的气液两相分布。喷雾锥外侧显示出明显分界面，但分界面处水体积占到20%左右。综合考虑网格大小及雾化颗粒尺度，定义水体积份额1%～5%为喷雾锥边界，如图4b所示，该边界较窄，可据此测定喷雾头的喷雾锥角值为92°。

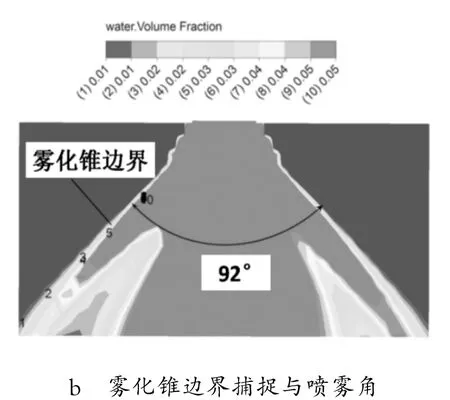
图4 水体积份额云图及雾化锥角的确定

1.2 试验验证

前期设计的小流量单螺旋喷雾头已开展了冷态喷雾特性试验，利用其已有试验数据对上述数值方法进行验证。

1.2.1 流量特性计算结果验证

试验在额定流量（11.7 t/h）的75%、80%、100%、120%、125%下测定喷雾头对应的压降。在数值模拟中，通过设置对应的入口流量值，得到相应的压降计算值，数值模拟所得结果与试验结果均列于表1中。可以看出，模拟结果较试验结果偏低，误差在10%以内，可以较好地预测喷雾头进出口压降。

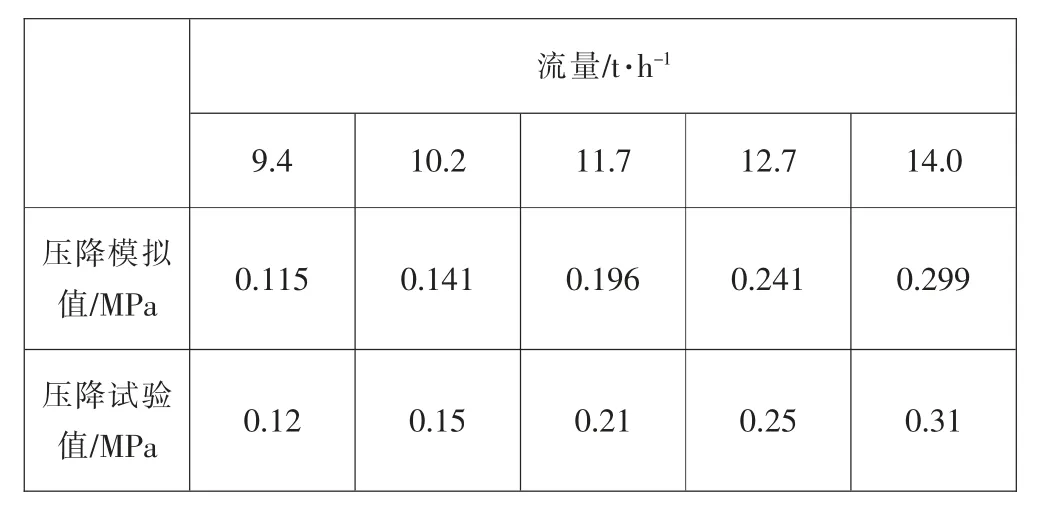
表1 进出口压降模拟值与试验值比较

1.2.2 雾化锥角计算结果验证

雾化锥角测定用于评价喷雾头雾化液滴范围，试验分别在各流量下采用照相进行雾化锥角测定。数值模拟所得结果与试验结果均列于表2中。相比试验结果，模拟值均偏小，但不同流量下模拟与试验所得的雾化锥角具有相同的变化趋势。

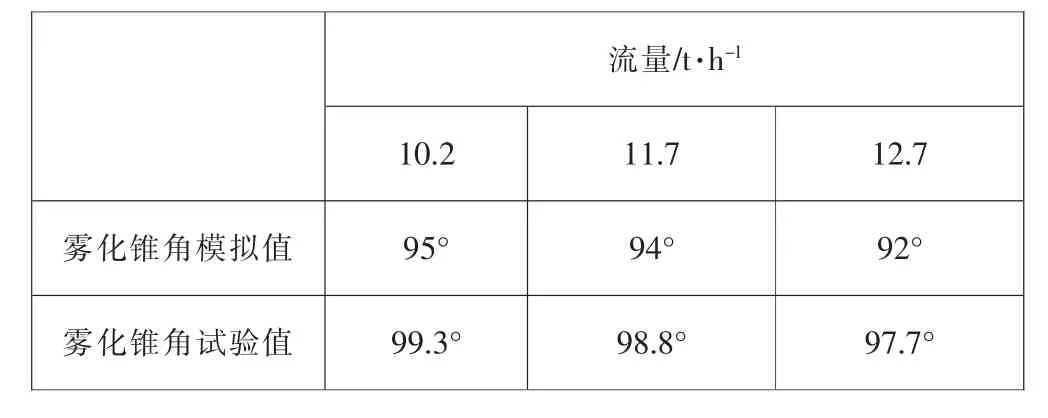
表2 雾化锥角模拟值与试验值比较

上述结果证明本文采用的数值计算方法和计算模型合理可行，能够有效地预测喷雾头的压降及喷雾锥角。

2 大流量单螺旋喷雾头的结构优化

为设计一种冷态额定流量达30t/h、压降小于0.2MPa、喷雾角大于55°的大流量喷雾头，在借鉴同类单螺旋喷雾头及查阅相关设计资料的基础上，初步确定了喷雾头的主要结构尺寸。在开展冷态试验前，采用上述数值模拟方法对喷雾头性能进行预测。在计算过程中，重点考察了喷嘴混合室导锥角β、内芯螺旋升角γ对喷雾性能的影响（β和γ的定义见图5）。

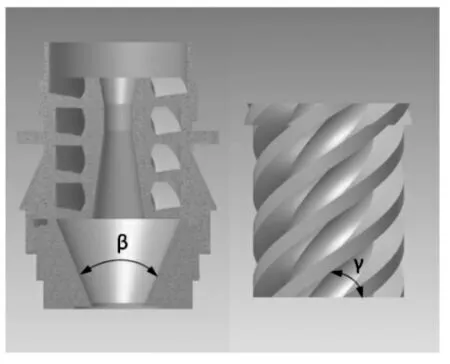
图5 混合室导锥角β与内芯螺旋升角γ

2.1 混合室导锥角对喷雾性能的影响

为研究混合室导锥角β对喷雾性能的影响，保持螺旋升角γ=30°不变，通过数值计算考察不同β值（30°、45°、60°、100°）对进出口压降、喷雾角等的影响。

图6给出了不同β角度下喷雾头进出口压降与流量的关系曲线。在额定流量下，各喷雾头的压降均远小于0.2 MPa，满足设计要求。随着β角的增大，进出口压降有所增大，即喷雾头的流量系数减小（流量系数越小代表阻力损失越大）。这是因为混合室导锥角增大时，螺旋流道流体与中间流道流体发生更为激烈的冲撞混合，从而使压力损失增大。

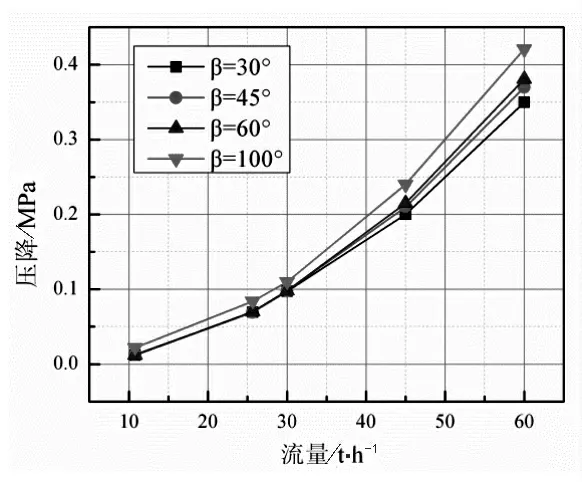
图6 不同混合室导锥角β下流量特性

表3给出了4个喷雾头在额定流量下的雾化锥角计算值，雾化锥角随导锥角增大而增大。在满足雾化锥角不小于55°前提下，喷雾头雾化锥角应尽可能地小，这样落入有效区域的液滴数量才尽可能地多，同时不会对稳压器内壁造成不必要的热冲击。因此，混合室导锥β设置为45°左右较为合适。

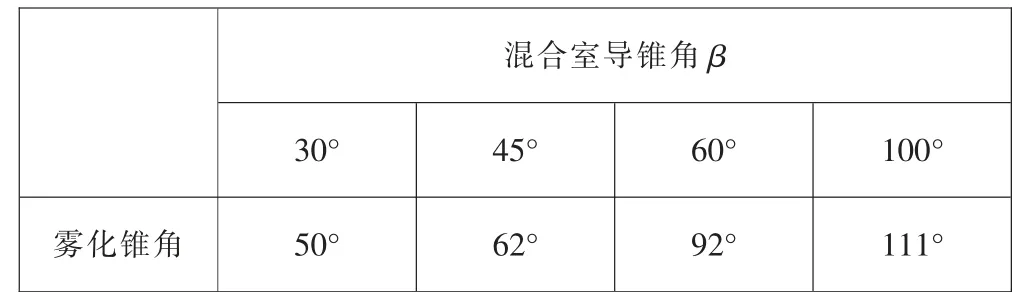
表3 不同混合室导锥角β下的雾化锥角

图7给出了导锥角β=60°喷雾头的外流场域中，距离喷雾头出口不同距离截面上的水体积分数云图。可以看出，液体喷出后会逐渐形成空心区域，这是由于出口截面各点切向速度的不均匀引起的，是由螺旋结构的特点所决定的。

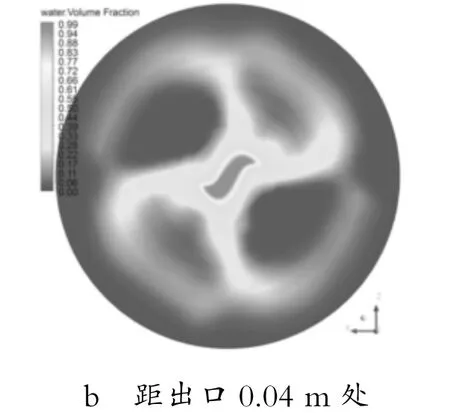
图7 距出口不同距离截面处水体积分数

图8 给出了混合室角度60°和45°的两种喷雾头距出口0.1m截面处的水体积分数云图。可以看出，当混合室角度减小，即混合室长度增大时，空心锥现象明显改善，喷雾分布更加均匀。图8b中心区域最大水体积分数为0.78，而图8a中心区域为0.99。这说明混合室角度为45°的喷雾头，其中心部分与空气接触更为充分，冷却效果也会更好。