基于混沌时间序列的黄土滑坡变形预测方法及应用

王 利，岳 聪，舒 宝*，张耀辉，许 豪，义 琛

(1. 长安大学 地质工程与测绘学院，陕西 西安 710054； 2. 地理信息工程国家重点实验室，陕西 西安 710054； 3. 长安大学 西部矿产资源与地质工程教育部重点实验室，陕西 西安 710054； 4. 自然资源部第一大地测量队，陕西 西安 710054)

0 引 言

滑坡本质上是一个开放、耗散和复杂的非线性动力学系统。在采用基于变形数据的滑坡预测模型(灰色系统模型[1-3]、指数平滑模型[4-6]等)进行变形预测时，由于没有考虑所研究系统确定性与随机性的关系，所以在一定程度上会影响预测结果的准确性[7]。混沌理论是一种非线性系统预测方法，主要研究自然界复杂系统的发展规律，可以直接根据序列本身的客观规律进行预测，减少了人为因素的干扰，使得预测结果可靠性更高。尽管混沌系统自身对初始条件的敏感性导致了对其行为进行长期预测的困难，但是并没有影响到对混沌系统发展规律的研究[8]。目前，混沌理论已广泛应用于经济学、气候、电力等领域[9-16]。

已有研究表明，滑(边)坡在演化过程中会通过一定途径进入混沌状态[17-21]。基于此，本文基于陕西泾阳地区庙店滑坡GNSS变形监测数据序列与经过抑噪处理后的数据序列，在判定两种变形监测数据序列为混沌时间序列的基础上，引入几种常见的混沌时间序列预测方法，并对这些方法的预测结果进行比较，以便选取适用于黄土滑坡变形预测的方法；同时，对这两种数据序列分别进行预测结果的对比分析，判断对原始监测序列进行抑噪处理后是否可以提高滑坡变形监测结果的预测精度。

1 理论模型

1.1 混沌相空间重构理论

混沌理论作为一种非线性系统理论，主要通过研究如何由时间序列通过相空间重构，从另一个维度和视角来辨识系统，挖掘系统中蕴藏的规律，并预测系统的未来走势。在这个过程中，相空间重构的质量直接影响到系统的未来走势。因此，需要采取有效且合适的方法重构相空间。Takens认为相空间重构最有效的方法为延迟坐标法[22]，其基本原理如下。

设时间序列为{x(i),i=0,1,2,…,N}，N是时间序列长度，以时间延迟(Δt)和嵌入维数(m)进行相空间重构，相空间中相点(Xi)的表达式为

Xi=

(1)

也可以表示为

Xi=[x(i),x(i+Δt),x(i+2Δt),…,

x(i+(m-1)Δt)]i=1,2,…M

(2)

M=N-(m-1)Δt

式中：M为相空间中相点的个数。

时间延迟和嵌入维数是相空间重构的两个重要参数，这两个参数的选取是否合理将直接决定相空间重构的质量。

相空间重构的延迟坐标法原理表明，由系统原始状态变量构成的相空间和一维观测值重构相空间里的动力学行为等价(拓扑学认为两个空间是相同的)，即一维观测值中包含系统所有状态变量演化的全部信息。由此演化规律可得到系统下一时刻的状态，从而得到时间序列下一时刻的预测值，这就为采用混沌时间序列预测提供了依据。

1.2 S-变换时频滤波

变形序列的噪声会直接影响变形预测结果，因此，本文采用S-变换时频滤波方法削弱GNSS坐标序列的噪声，其原理如下。

S-变换滤波过程的表达式为

h(t)=S-1(S(h(t))×HTF(τ,f))

(3)

(4)

式中：t为时间;f为频率;τ为控制窗口移动的参数;h(t)为给定的时间信号;HTF(τ,f)为时频滤波器;S和S-1分别为正变换与逆变换；D为指定信号的时频通域。

由于变形监测过程中随机噪声分布在各个时间点处，所以D为整个时频通域。

时间信号h(t)经过S-变换后得到二维复时频矩阵S(t,f),将S(t,f)中各元素求模后的矩阵记为S|(t,f)|。由S-变换结果可知，时频滤波器的设计主要有两种方式：①根据S(t，f)设计滤波器；②根据S|(t，f)|设计滤波器。第一种方式会改变系数的相位，从而使S-逆变换重构得到的时域信号产生附加噪声，因此，本文根据最大最小值理论，按照S|(t，f)|设计滤波器。定义如下时频滤波器，其表达式为

(5)

式中：Mi为ti时刻振幅谱中S|(ti,f)|的最小值。

具体抑噪过程如图1所示。

图1 基于S-变换的抑噪过程

2 实验分析

2.1 数据来源

本文所采用的观测数据来自陕西省泾阳县太平镇庙店村，该村位于泾河南岸，是黄土滑坡频发地带。滑坡体平面形态呈“上陡下缓”的形态[图2(a)]。

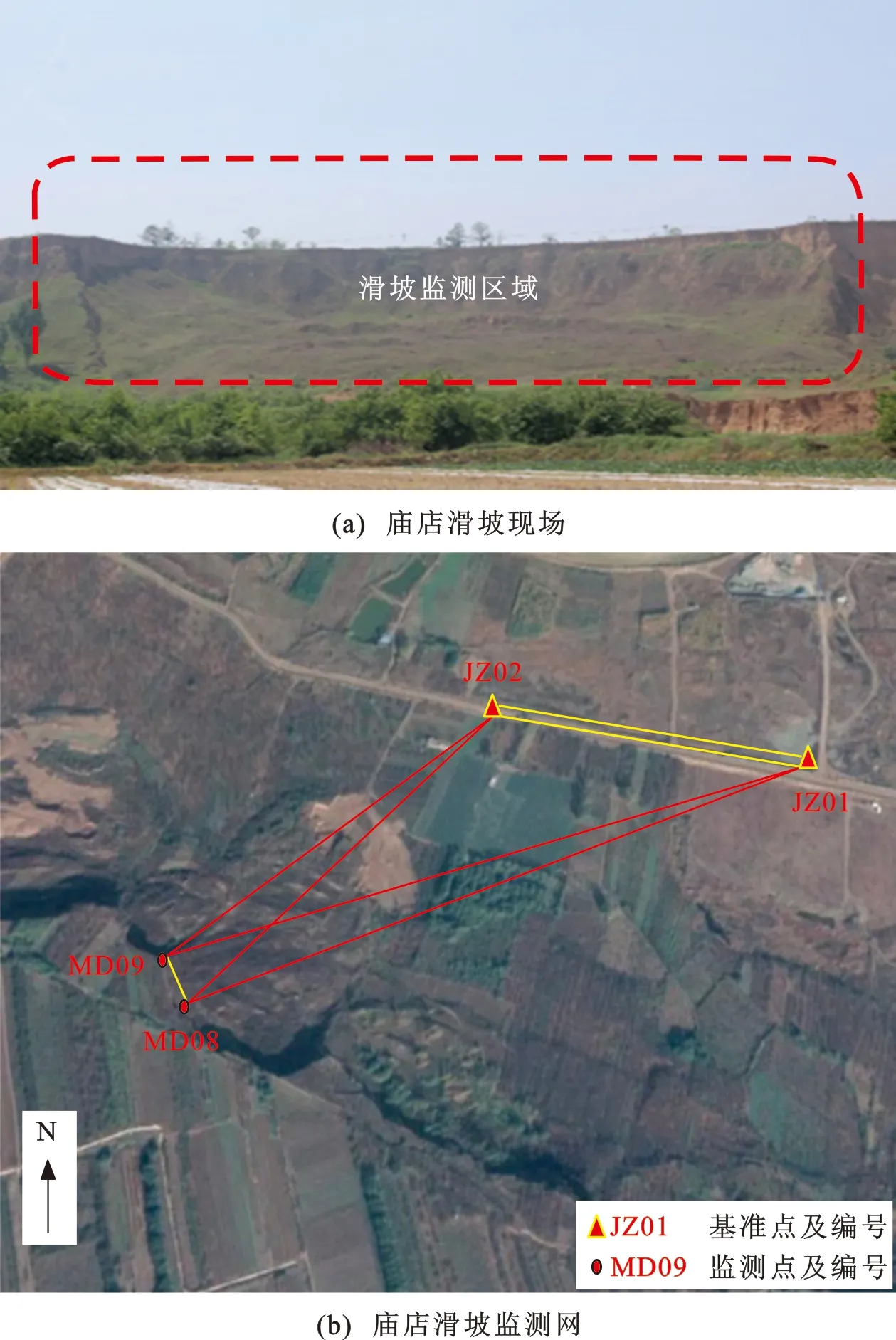
图2 陕西泾阳地区庙店滑坡现场及监测网

滑坡监测网[图2(b)]中使用北斗/GNSS接收机进行观测，并结合长安大学北斗分析中心自主研发的北斗/GNSS实时监测系统获得的监测点N(北)、E(东)、U(高程)方向点坐标变化序列的小时解，数据采集时间为2018年8月28日17:00到2019年4月17日2:00，共1 913个历元，基准站设在距离滑坡体约400 m处的稳定地带。本文选取MD09监测点坐标变化序列进行分析。由于GNSS信号易受干扰，所以对MD09监测点GNSS变形监测结果采用S-变换时频滤波方法进行抑噪处理[23]，结果如图3所示。

图3 原始数据序列和S-变换抑噪后的数据序列

2.2 滑坡变形时间序列的相空间参数重构

时间延迟和嵌入维数是相空间重构的两个重要参数。本文以MD09监测点E方向GNSS变形监测序列和经S-变换抑噪处理后的GNSS变形监测结果序列为例进行相空间参数确定。

2.2.1 时间延迟的确定

在实际应用中，时间延迟的选取主要有平均位移法、自相关函数法以及互信息量法[24]。其中，自相关函数法主要利用相空间中各相点的线性相关性求解时间延迟。尽管该方法简单易实现，但该方法不能推广到高维相空间重构过程。互信息量法则是在考虑了以上方法的局限性之后提出的一种解决时间延迟比较有效的方法。本文采用互信息量法求解MD09监测点E方向滑坡变形时间序列的时间延迟(图4)。

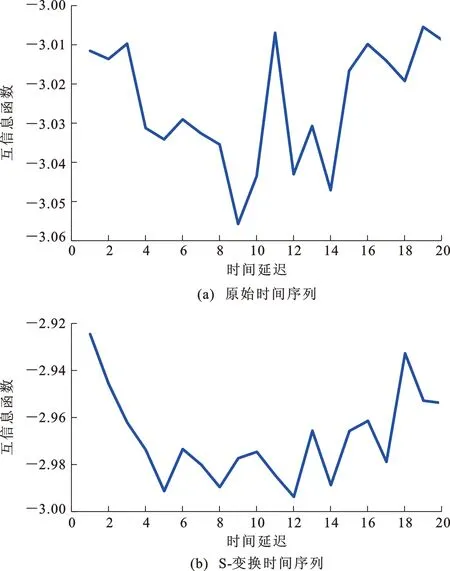
图4 MD09监测点E方向变形时间序列时间延迟t

从图4可以看出，MD09监测点的滑坡变形时间序列互信息函数随时间延迟变化明显。随着时间延迟的增大，互信息函数有明显波动，这主要是因为利用互信息量法能够很好地反映MD09监测点各时间序列的相关性以及整个时间序列的非线性性质。因此，该方法适用于确定滑坡变形时间序列的时间延迟。当时间延迟为2时，原始时间序列的互信息函数取得第一个极小值[图4(a)]，因此，原始时间序列的时间延迟为2；当时间延迟为5时，原始时间序列的互信息函数取得第一个极小值[图4(b)]，因此，原始时间序列的时间延迟为5。

2.2.2 嵌入维数的确定

常用确定嵌入维数的方法有虚假邻近点法、改进的虚假邻近点法(Cao算法)以及饱和关联维法(G-P算法)。Cao算法是在虚假邻近点法的基础上针对其存在的不足改进而来，G-P算法和Cao算法在计算最佳嵌入维数时都容易实现，而且两种方法所得结果可以相互论证[25]。因此，本文采用Cao算法获取MD09监测点E方向变形时间序列的嵌入维数(图5)。

图5 MD09监测点E方向变形时间序列的嵌入维数m

从图5可以看出：采用Cao算法计算所得嵌入维数的均值(E(m))受嵌入维数影响较小，其值在1附近有小幅度的波动，整体趋近于1。令E1(m)=E(m+1)/E(m)，E1(m)随嵌入维数的变化而变换；当嵌入维数增加到某一个值后，E1(m)也趋于稳定。这说明监测点变形时间序列在计算之前所假定嵌入维数的范围内，没有因取值太小出现数据冗余，也没有因取值太大遗漏部分数据或丢失数据间的相关关系。因此，计算结果较好，进而说明在泾阳地区庙店滑坡变形时间序列的相空间重构过程中，可以采用Cao算法确定最佳嵌入维数。

当嵌入维数增加到10时，E1(m)不再随着维数的增加而改变[图5(a)]，因此，原始时间序列E方向上的嵌入维数为10；当嵌入维数增加到8时，E1(m)不再随着维数的增加而改变[图5(b)]，因此，原始时间序列E方向上的嵌入维数为8。

2.3 黄土滑坡混沌时间序列预测性能分析

2.3.1 黄土滑坡混沌时间序列的判别

运用混沌理论研究时间序列的前提是该序列具有混沌特性，因此，需要进行MD09监测点GNSS变形序列混沌特性的识别。时间序列的混沌特性判定方法主要分为定性和定量两个方面。定性判定方法简单、直观、方便，但该方法受人为主观因素影响较大，导致对时间序列的混沌特性判别不准确；而定量判定方法主要是对通过计算满足混沌特性的相关量值进行判定，避免了人为因素的影响。因此，本文采取定量判定方法中的Lyapunov指数进行时间序列的混沌特性识别。

Lyapunov指数的求解主要有wolf法和小数据量法，其中，小数据量法计算简单且易于实现，适合处理有限长度的时间序列[26]。因此，本文采用小数据量法求解时间序列的Lyapunov指数。图6为采用小数据量法分别计算的MD09监测点E方向原始时间序列和经过S-变换抑噪处理的时间序列最大Lyapunov指数。计算结果表明：原始时间序列最大Lyapunov指数为0.001 2，经过S-变换抑噪处理的时间序列最大Lyapunov指数为0.001 0，两种时间序列的最大Lyapunov指数均大于0，为正数。因此，采用GNSS技术获取的滑坡变形时间序列具有混沌特性，可以采用混沌理论分析GNSS滑坡监测数据。

图6 MD09监测点E方向变形时间序列最大Lyapunov指数

2.3.2 GNSS混沌时间序列变形预测

本文采用的变形监测数据来自陕西泾阳地区庙店滑坡，监测时间序列共计1 913历元(即每小时采一次样)，其中前1 883历元为训练数据，后30历元为预测数据。对MD09监测点的变形监测数据分别采用加权一阶局域预测方法、最大Lyapunov指数预测方法以及BP神经网络预测方法进行预测，预测方式选择多步预测。为了更好地分析监测数据经不同方法预测后的精度，采用平均绝对误差(MAE,δMAE)和平均相对误差(MRE,δMRE)两个评价指标来评价预测方法的精度。其表达式为

(6)

(7)

对MD09监测点E方向混沌时间序列进行预测，根据已经求出的时间延迟和嵌入维数对监测点原始序列进行相空间重构，并通过不同预测方法对序列后30历元数据进行预测，预测结果如图7所示。由图7可以看出：采用加权一阶局域预测方法和最大Lyapunov指数预测方法的预测结果变化趋势与原始时间序列的变化趋势大致相同，但预测值与原始时间序列实际值相差较大，最大偏差分别为2.4 mm和1.5 mm。相比较而言，BP神经网络预测方法的预测值较为接近原始时间序列实际值，最大偏差为1.1 mm。为了定量比较3种预测方法的预测精度，本文分别计算了不同预测方法的绝对误差、相对误差两个评价指标序列(图8、9)。从3种预测方法对应的评价指标序列可以看出，BP神经网络预测方法优于加权一阶局域预测方法与最大Lyapunov指数预测方法，尤其是对前10历元的预测，其预测结果的相对误差在15%以内，绝对误差在0.5 mm以内。整体而言，原始时间序列的预测值与实际值偏差较大。

图7 MD09监测点E方向变形时间序列预测结果

图8 MD09监测点E方向变形时间序列各模型相对误差

2.3.3 基于S-变换的GNSS混沌时间序列变形预测

为了分析经S-变换抑噪处理后的预测效果，根据已经求出的时间延迟和嵌入维数对监测点原始序列进行相空间重构，并建立不同预测方法对序列后30历元数据进行预测，预测结果如图10所示。从图10可以看出：加权一阶局域预测方法与最大Lyapunov指数预测方法预测值与实际值偏差较大，最大偏差分别为0.8 mm和1.3 mm。而BP神经网络预测方法的预测值比较接近实际值，最大偏差为0.3 mm，且与实际值序列具有相同的波动趋势。为了定量比较3种预测方法的预测精度，本文分别计算了不同预测方法的绝对误差、相对误差两个评价指标序列(图11、12)。从3种预测方法对应的评价指标序列可以看出，BP神经网络预测方法优于加权一阶局域预测方法与最大Lyapunov指数预测方法，尤其是对前10历元的预测，其预测结果的相对误差在5%以内，绝对误差在0.3 mm以内，基本能反映原始时间序列的变化特征。在前10历元预测精度高，主要是因为混沌的不稳定性以及初值敏感性，导致混沌时间序列只能是短期预测。相比较而言，在S-变换抑噪处理之前，GNSS混沌时间序列的预测值与实际值偏差较大，其主要是在对GNSS原始时间序列进行相空间重构时，由于受到观测噪声的影响，混沌时间序列的奇异吸引子不能完全恢复，所以预测结果偏差较大。

图9 MD09监测点E方向变形时间序列各模型绝对误差

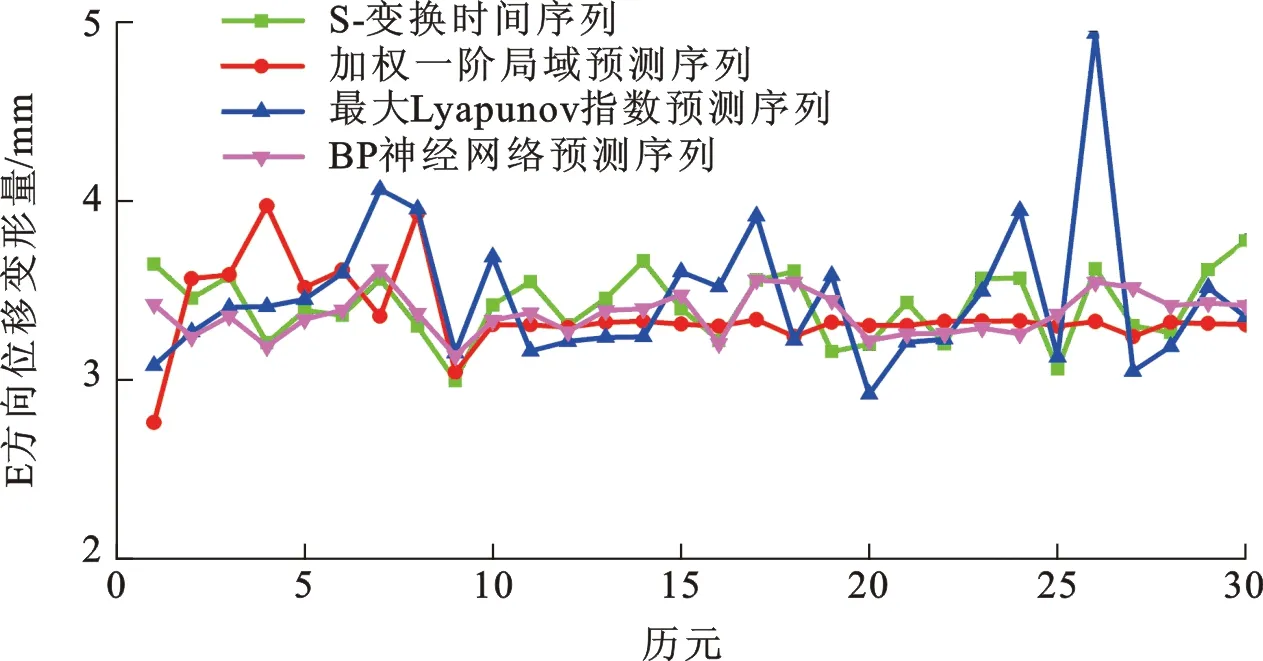
图10 S-变换抑噪后时间序列预测结果

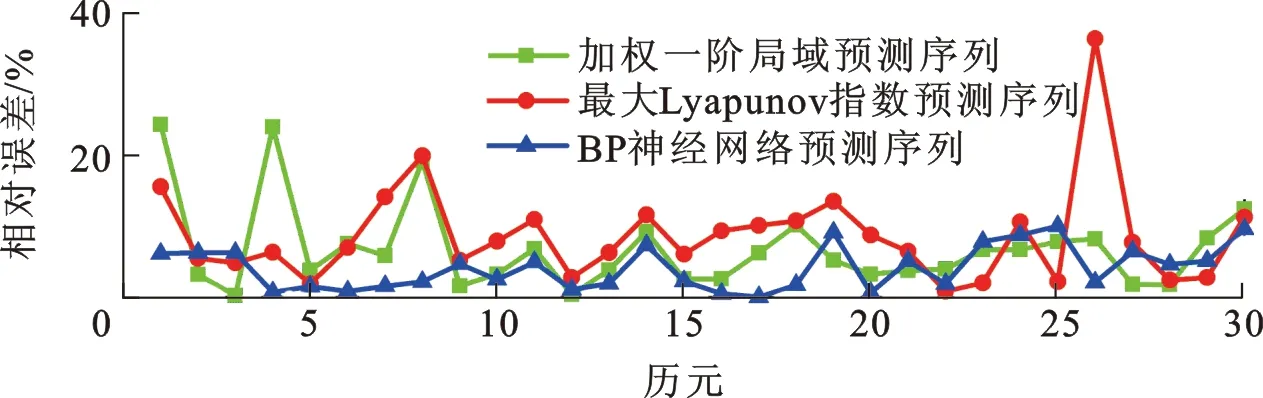
图11 S-变换抑噪后时间序列各模型相对误差

通过对比图11与图12可知，相较于原始数据预测结果，经过S-变换抑噪处理后的预测结果更加接近实际值，说明抑噪处理能够提高数据的预测精度。为了进一步说明抑噪处理后的数据有较高的预测精度，本文通过平均绝对误差和平均相对误差两项指标对预测结果进行分析，结果如表1所示。

图12 S-变换抑噪后时间序列各模型绝对误差

通过表1可以看到，经过S-变换抑噪处理后的时间序列预测结果的平均绝对误差与平均相对误差均小于原始时间序列预测结果的评定指标。其中，加权一阶局域预测方法、最大Lyapunov预测方法和BP神经网络预测方法经S-变换抑噪处理后的时间序列的平均绝对误差与原始时间序列相比分别提高了66.7%、57.1%和75.0%，平均相对误差分别提高了58.5%、56.5%和65.5%。这说明原始数据存在的噪声对预测结果有较大的影响，且经过抑噪处理后预测效果有较明显的提高。不管是原始时间序列，还是经过S-变换抑噪处理后的时间序列，采用3种预测方法后，BP神经网络预测方法的平均绝对误差与平均相对误差均小于其他两种预测方法预测结果的评定指标。经过原始时间序列预测的平均绝对误差和平均相对误差分别为0.4 mm和11.9%；经过S-变换抑噪处理后的时间序列预测的平均绝对误差和平均相对误差分别为0.1 mm和4.1%。

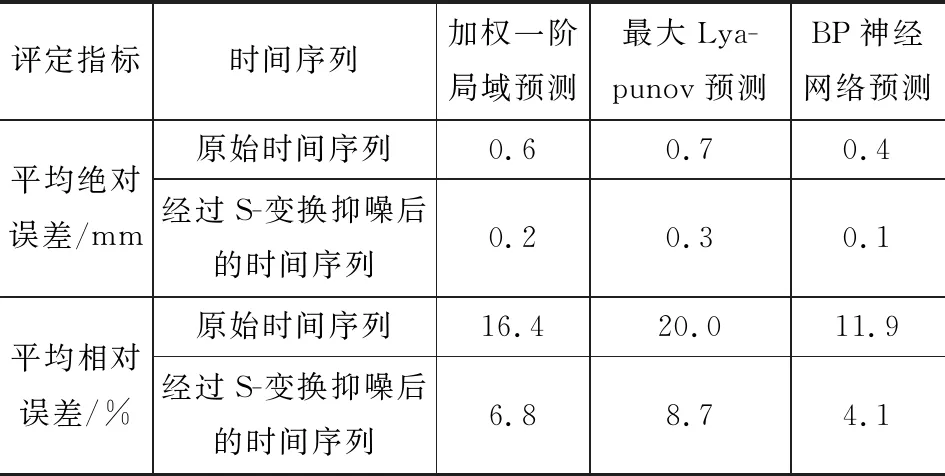
表1 不同时间序列各模型预测精度统计结果

3 结 语

由于滑(边)坡变形普遍具有非线性性质，且在演化过程中会通过一定途径进入混沌状态。如果不考虑滑(边)坡系统确定性与随机性之间的关系，在一定程度上会影响预测结果的准确性。为此，本文结合陕西泾阳地区庙店滑坡GNSS变形监测数据，采用基于混沌理论的滑坡变形时间序列预测方法对该滑坡的变形时间序列进行了分析和预测。

(1)采用相同方法对GNSS滑坡变形监测的原始时间序列和经过S-变换抑噪处理后的时间序列求解各自的相空间重构参数，并进行混沌识别。结果表明：GNSS滑坡变形监测的原始时间序列与经过S-变换抑噪处理后的时间序列均具有混沌特性。

(2)采用不同的混沌时间序列预测方法对庙店滑坡GNSS变形监测的原始时间序列与经过S-变换抑噪处理后的时间序列分别进行预测。结果表明：经过S-变换抑噪处理后的时间序列预测结果更接近实际值，平均绝对误差、平均相对误差均优于原始时间序列的指标评定值；多种预测方法中，BP神经网络预测方法的预测精度较好；GNSS变形监测原始时间序列预测的平均绝对误差和平均相对误差分别为0.4 mm和11.9%，经过S-变换抑噪处理后的时间序列预测的平均绝对误差和平均相对误差分别为0.1 mm和4.1%。综上所述，GNSS变形监测原始时间序列中存在的噪声对变形预测结果有较大影响；经过S-变换抑噪处理后，预测效果得到明显改善。