基于模糊逻辑的收费广场动态容量分配方法

李俊辉

摘要：文章提出了一种基于模糊逻辑的方法来控制车辆收费数量，以确保以最少的费用达到期望的服务水平。针对最小和最大等待时间约束下的期望服务水平，提出了收费广场容量控制的质量准则，并将该准则应用于模糊逻辑控制方法的性能评价。为了测试模糊逻辑控制方法，采用随机排队论模型作为Matlab/Smulink仿真模型，利用交通流密度的估计值检验了所实现模型和控制器对系统行为预测的可用性。

关键词：收费广场;模糊逻辑控制方法;马尔可夫过程;动态容量分配

中图分类号：U491.1⁺23文献标识码：ADOI：10.13282/j.cnki.wccst.2021.01.050

文章编号：1673-4874（2021）01-0185-04

0引言

近年来，道路运输系统发生了重大变革，其重点不再仅仅是修建连接各个目的地的道路，而实时导航、安全和环保驾驶、旅行舒适性、驾驶员辅助、避免事故的快速反应和道路交通基础设施的最佳使用，正变得越来越重要。因此，为了保证交通系统容量的有效利用，需要在交通系统中增加控制系统。这些控制系统使交通基础设施能够对交通流或天气条件的变化做出自主响应，例如将服务车道激活为全车道以增加最大可能的交通流，激活动态交通标志以告知驾驶员新的路况，改变车辆的路线以避免拥挤或事故等情况[1-2]。

通过观察排队长度，可以手动确定收费站的通行能力。当排队长度超过其规定的最大值（由收费站广场管理人员确定）时，活动收费站的数量可能会增加，反之亦然。这种方法的一个明显的缺点是，为了引起通行能力的变化，首先交付的收费站服务水平必须显著降低;或者在另一种情况下，排队长度必须显著缩短，才能减少有效的收费站数量。在这两种情况下，都没有有效地分配容量[3-4]。当使用这种“手动”方法时，可能会出现另一个问题：在给定的时间内，收费站广场现场没有足够的工人，因此并非所有可用的收费站都可以使用。在这种情况下，系统对动态变化的响应会变慢甚至变长，导致交通拥挤和不必要的等待时间。在使用智能控制系统进行收费广场容量分配或预测时，可以避免或减少这种问题。本文提出了一种基于模糊逻辑的收费广场动态容量分配控制系统。

1收费站广场服务水平问题

对收费设施的性能评估需要充分了解其独特的特性和约束条件，并定义有助于解释用户感知到的服务水平的正确有效性度量（MOEs）。排队长度和排队时间是反映收费系统运行状况和用户感知服务水平的两个最重要的MOE。本文将排队等待服务的时间作为评价模糊控制器性能的主要指标。定义的服务水平框架包括6个服务水平等级，表1给出了规定的等待时间间隔。

2收费站广场模式

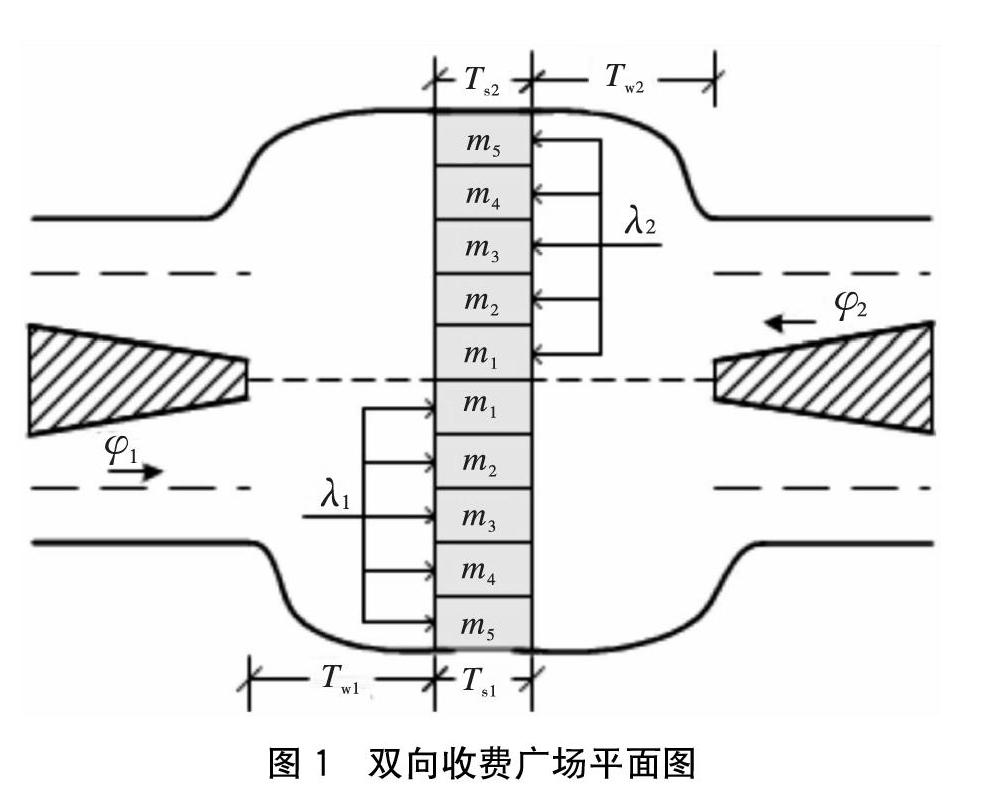
如图1所示，一般双向收费广场由进站车道、排队区、收费站和出站区组成。在收费方面，收费站可以是活动的或空闲的，并且只能分配给交通流的一个方向。一般来说，如果每个方向的交通条件允许，则在交通流方向之间可以共享一定数量的收费站（例如，一个方向的输入交通负载大于另一个方向的输入交通负载）。

图1中的可变索引表示交通流的两个方向之一。本文只考虑收费站广场的一个交通流方向，但只有固定数量的活动收费站，没有本文提出的控制部分。收费广场共有10个收费站，每个车流方向5个。为了简化计算，在分析中，假设所有10个收费站都采用了经典的支付方法。

建议的收费站广场模型可以用以下公式进行数学描述，见式（1）～（4）：

A=λ·Ts（1）

（2）

（3）

（4）

其中A是交通荷载（即在任何给定时刻预期占用的收费站数量），而ρ是单个收费站的交通荷载。收费广场模型的输入变量为交通流强度λ和活动收费站数量m。输入交通流强度取决于特定的交通状况。主动收费站的数量将使用当前主动收费站的数量及其从模糊逻辑控制方法获得的变化来计算。模型输出值是队列中的平均等待时间T_w和队列长度L_w。

3模糊逻辑控制方法

本文所提出的模糊逻辑控制方法可动态地改变收费站的数目，即相对于收费站广场上的输入交通负荷而变化。这意味着控制器必须获得关于收费站广场上当前排队车辆数量的信息，而且必须获得关于特定服务水平等级和特定数量的活动收费站允许的最大排队长度的信息。例如，使用表1中的数据，参考式（1）～（4），T_s平均值为21s。可计算出，在4个有效收费站情况下，如果累计最大排队长度平均不超过7.6辆（每个收费站前1.9辆），则可以维持D级服务水平。当前队列长度L_wt和允许特定类的最大队列长度L_wLaS之间的差异被定义为所提出的模糊控制器的第一个输入变量，见式（5）：

L_w1=L_w2-L_WLOS（5）

如果式（5）的结果为正数，则当前服务水平低于预定值，并且可以减少有效收费站的数量。在相反的情况下，如果结果是负数，则当前服务水平高于预定值，并且应增加有效收费站的数量。由于L_w1的值可以振蕩±1辆车，且在如此小的偏差下，改变收费站广场的通行能力是无效的，因此有必要为L_w1定义不同的模糊集。本文定义了五个语言变量：+LD（大正差）、+SD（小正差）、ND（无差）、-SD（小负差）和-LD（大负差）。对于两个集合（+LD和-LD），定义了梯形隶属函数，对于其他三个集合（-SD、ND和+SD），使用三角形隶属函数。

建议的模糊逻辑控制方法（L_w2）的第二个输入变量表示两个连续15min间隔内当前队列长度之间的差异，见式（6）：

（6）

其中t和t-1分别表示两个连续的15min间隔。为了对第二输入变量L_w2进行分级，定义了五个模糊集：Ll（大增）、Sl（小增）、NC（无变化）、SD（小减）和LD（大减）。

提出的模糊控制器输出变量代表了对收费广场管理人员的指令，即使增加或减少有效收费站的数量，还是保持不变。与两个输入变量类似，定义了五条指令，表示完成推理过程所需的五个语言变量。名称和符号等于第二个输入变量L_w2，但含义不同。这个数字可以改变如下：（i）增加2，（ii）增加1，（iii）没有变化，（iv）减少1和（v）减少2。每个输入变量有2个输入变量（L_w1和L_w2和5个语言值，总共可以定义25个模糊规则。

通过对进站交通流动力学的检验和仿真试验，得出结论：较小的模糊规则集（<10）可以得到较好的收费广场通行能力分配。在不同的设置和输入值下进行了一系列的测试和仿真，对于聚合系统，选择了规则析取系统和均值最大隶属度解模糊方法。

4仿真结果

针对所提出的控制方案，在Matlab/Simulink中实现了适当的模型评估。其方案如图2所示。由图2可见，模型的组成部分有：准备输入信号的模糊逻辑控制方法模块和收费广场模型模块。收费站-广场模型有两个输入：关于活动收费站数量变化的指令和进入的交通流强度。该模型得到不同的输出，但与研究最相关的是队列长度。队列长度是所提出的控制方案中使用的变量。其他输出包括详细分析所需的信号：排队车辆的累计数量、等待时间（累计和每个活动收费站）、收费站广场交通负荷和当前活动收费站的数量。

控制方案建议输入与平均等待时间成正比的参考队列长度，见式（4）。在模拟中，将D类定义为要维护的类，因此每个活动收费站的参考队列长度必须设置为2。对于首次提出的控制方案的性能评估，只分析了收费站广场上的一个交通流方向。使用的参数如下：

（1）最低收费站数目设为2个。

（2）最大活動收费站数量设置为5。

（3）平均服务时间设置为21s。

平均服务时间的值是通过在克罗地亚的现金支付收费站进行的测量得出的。活动收费站的初始数量设置为2。

获得的数据记录还包含有关测量时间和通过测量点的车辆类型的信息。在每个测量点上记录两个行驶方向的数据。交通流量测量以1h为间隔采样。为了得到适合仿真的输入交通流数据，对一个交通流方向的车辆类别进行了求和，使用样条策略对时间间隔的丢失数据进行插值。该插值的结果如图3所示。（如前所述，Ts值是从收费站的平均服务时间测量中收集的）。

图4描绘了1d中活动收费站数量的变化。可以看出，目前还没有达到最大的收费站数量。此外，很明显，当前活跃的收费站（全线）的数量与图3中输入的交通流数据大致匹配，这证明控制器对动态输入做出了适当的反应。例如，在午夜，当存在最小交通流强度时，控制器希望减少活动收费站的数量（虚线），但这是不可能的，因为定义的活动收费站的最小数量被设置为2。当交通流强度增加时，管制员会做出反应，并发出增加收费站数量的指令。高峰过后，交通流强度开始急剧下降（如图3所示）。在这种情况下，模糊逻辑控制方法发出指令，以减少主动收费站的数量。很明显，在这两种情况下（在交通流量增加和减少的过程中），模糊逻辑控制方法都会做出适当的反应，即控制器希望保持设定为D类的期望服务水平等级。

对图4和图5所示的仿真结果的并行分析表明，任何活动收费站数量的增加都会导致等待时间的减少。

如上所述，为了对所提出的模糊逻辑控制方法进行定量评估，使用了服务水平等级。每个类都有自己的等待时间间隔。由于我们将期望的服务水平等级设置为D，图5显示了该等级的上下Tw边界。基于这些结果，可以得出结论，模糊逻辑等待时间分析控制器完成了它的任务。具体地说，尽管输入的交通流强度在白天发生了显著的变化，但是在活动收费站的数量（见图4）只有4个变化的情况下，在整个模拟时间（24h）内保持所需的D类。图5所示的等待时间结果表明，在模拟期间（全线），收费站广场的服务水平处于D级或更好。

除了Tw评估参数外，另一个重要的参数是队列中的平均车辆数，即平均队列长度。分析结果如图6所示。本文提供了两组数据：排队车辆的累计数量（即收费广场上等待服务的车辆总数）和每个活动收费站前面的车辆数量。这些集合分别用虚线和实线表示。为了得到平均值，将输出结果近似为最接近的高整数值。

因此，该模糊控制器对于提高收费广场的整体效率和预测未来的资源具有重要意义。

5结语

本文提出了一种用于收费广场动态容量分配的模糊逻辑控制方法。为便于评估，采用马尔可夫M/M/1模型对收费广场排队系统进行建模，建立了包含实际测量参数的Matlab/Simulink仿真模型，同时，利用实际交通流数据测量得到了真实的仿真结果。

结果表明，通过动态改变收费广场的通行能力，模糊逻辑控制方法能够成功地维持期望的服务水平等级。此外还表明，1d内只有4个活动收费站的数量变化，就可以达到并保持所需的服务水平。这证明了所提出的基于模糊逻辑的控制方法有效地分配了系统的容量，并有助于对所需资源做出可靠的预测。更重要的是，该控制器有助于确保相对稳定的服务水平，这对旅行计划和旅客的总体满意度非常重要。

参考文献

[1]张晨琛，王艳辉，贾利民.ETC系统对收费站服务水平的影响研究[J].交通运输系统工程与信息，2013，13（2）：147-152.

[2]刘斌，潘红，路小波.ETC车道数对收费站服务水平的影响仿真研究[J].公路交通科技，2008，25（1）：120-123.

[3]高睿晶，高速公路电子不停车收费效益分析[J].公路交通科技，2017，13（11）：282-285.

[4]程俊龙.ETC通道通行能力与服务水平确定方法研究[J].公路交通科技，2014，31（6）：133-137.