面向商业和居民混合的配电网短期负荷预测HGWOACOA-LSTMN方法

葛磊蛟，刘航旭，赵 康，李 华，张 波，李元良

面向商业和居民混合的配电网短期负荷预测HGWOACOA-LSTMN方法

葛磊蛟1，刘航旭1，赵 康2，李 华3，张 波4，李元良1

(1. 天津大学智能电网教育部重点实验室，天津 300072；2. 山东科技大学电气与自动化工程学院，青岛 266590；3. 国网辽宁省电力有限公司经济技术研究院，沈阳 110015；4. 中国人民解放军32654部队，济南 250024)

针对商业和居民混合的配电网负荷预测影响因素多样和随机性强的特点，提出了一种基于灰狼郊狼混合优化算法(HGWOACOA)和长短时记忆网络(LSTM)相结合的配电网短期电力负荷预测方法．为实现对电力负荷的多输入特征进行筛选和降维，本文采用最大信息系数法(MIC)对负荷与输入特征之间的非线性相关性进行量化，剔除无效特征，再采用因子分析(FA)法对历史数据、气象、温度等输入特征进行信息提取，实现对有效影响因素降维；综合考虑灰狼优化算法(GWOA)具有全局搜索能力强、收敛速度快的特点，郊狼优化算法(COA)具有区域探索能力强、求解精度高的特点，为突出两种算法优点并弥补两种算法的不足，提出HGWOACOA对LSTMN的隐藏层神经元个数和一次训练样本个数两种参数进行优化，克服了参数选取的困难．在保证预测精度的同时提升运行效率，实现基于HGWOACOA-LSTMN的配电网短期电力负荷高精度预测．以配电网某商业和居民混合负荷为例，验证了文中所述预测方法具有较好的精度和鲁棒性，同时提升了运行效率和简化模型输入特征的维数，证明本文所提方法的精确度和适用性．

配电网；短期负荷预测；因子分析；灰狼优化算法；郊狼优化算法；长短时记忆网络

随着我国经济和城市快速发展，商业和居民混合场景在城市配电网中所占比例显著提升，逐渐成为城市电网的重要组成之一．为有效保证城市配电网安全可靠、经济高效运行，精准的短期负荷预测至关重要．然而，商业和居民混合负荷，不仅受营业时间及居民消费水平影响，而且易受气温、风力等诸多因素影响，具有强非线性和随机性的特征，如何实现对其精准、快速短期预测，挑战大，值得深入研究．

短期电力负荷预测是电力系统优化调度、经济运行的重要依据，国内外学者们提出了一些方法，主要可分为两种类型[1-5]．其一是时序外推法，如线性回 归[1-2]、自回归移动平均法[3]等；其二是人工智能的预测方法，包括支持向量机(support vector machine，SVM)[4]、人工神经网络(artificial neural network，ANN)[5]等．然而，虽然方法不断地提出与改进，短期或者超短期负荷预测结果的精确性不断提高，但商业和居民混合负荷强随机性场景下，上述方法依然较难准确地把握其变化规律．另外，国内外对于商业和居民混合负荷的短期电力负荷预测研究涉及不多，大多集中在单一商业或单一居民负荷预测．文献[6]考虑到工作时间和气象因素的影响，提出了一种商业负荷预测模型，但预测采用线性模型，预测误差较大. 文献[7]采用小波变换和支持向量机对商业负荷时间序列进行建模预测，但模型未考虑气象等影响因素，鲁棒性较差．

长短时记忆网络(long short-term memory networks，LSTMN)适用于影响因素多且复杂随机性强的预测，正好贴合商业和居民混合负荷特色．然而，长短时记忆网络方法应用于负荷预测的主要问题有：一方面，现有的研究大多把重点放在输入数据的选择，并未充分考虑输入数据对负荷预测结果精准与稳定的干扰；另一方面，负荷预测模型超参数选择是预测精准的关键之一，如何选择最适合输入特征的模型超参数，现在缺乏较多的依据．

针对上述问题，本文提出了一种基于灰狼郊狼混合优化算法(hybrid grey wolf optimization algorithm with coyote optimization algorithm，HGWOACOA)和LSTMN相结合的配电网商业及居民混合短时负荷预测模型．针对商业和居民混合负荷的强非线性和随机性特点，首先采用最大信息系数(maximal information coefficient，MIC)法筛选输入特征，确定具有强相关性的影响因素，并利用因子分析(factor analysis，FA)法对多输入特征进行筛选和降维，作为负荷模型的输入．然后，提出一种灰狼郊狼混合优化算法，并通过该算法对长短时记忆网络模型的隐藏层神经元个数和一次训练样本个数两种参数进行优化，构建基于HGWOACOA的短期负荷预测模型．最后，以某区域商业居民混合的实际配电网负荷数据进行仿真计算，验证本文所述预测方法具有极高精确性和鲁棒性．

1 负荷预测输入特征分析

1.1 负荷预测影响因素分析

配电网商业和居民混合负荷预测的影响因素众多[8]，主要为历史负荷、日期类型和多种气象因素等.其中，历史负荷具有日周期性的特点，不同时刻的负荷显著不同；日期类型会影响商业场所的人流量和居民用电行为，导致休息日与工作日的负荷水平不一致；气象因素的变化会引起负荷的剧烈波动．综合考虑以上的影响因素，对负荷预测的原始输入进行梳理，如表1所示，其中假设预测时刻为，日期类型分为工作日与休息日．

表1 负荷预测输入特征

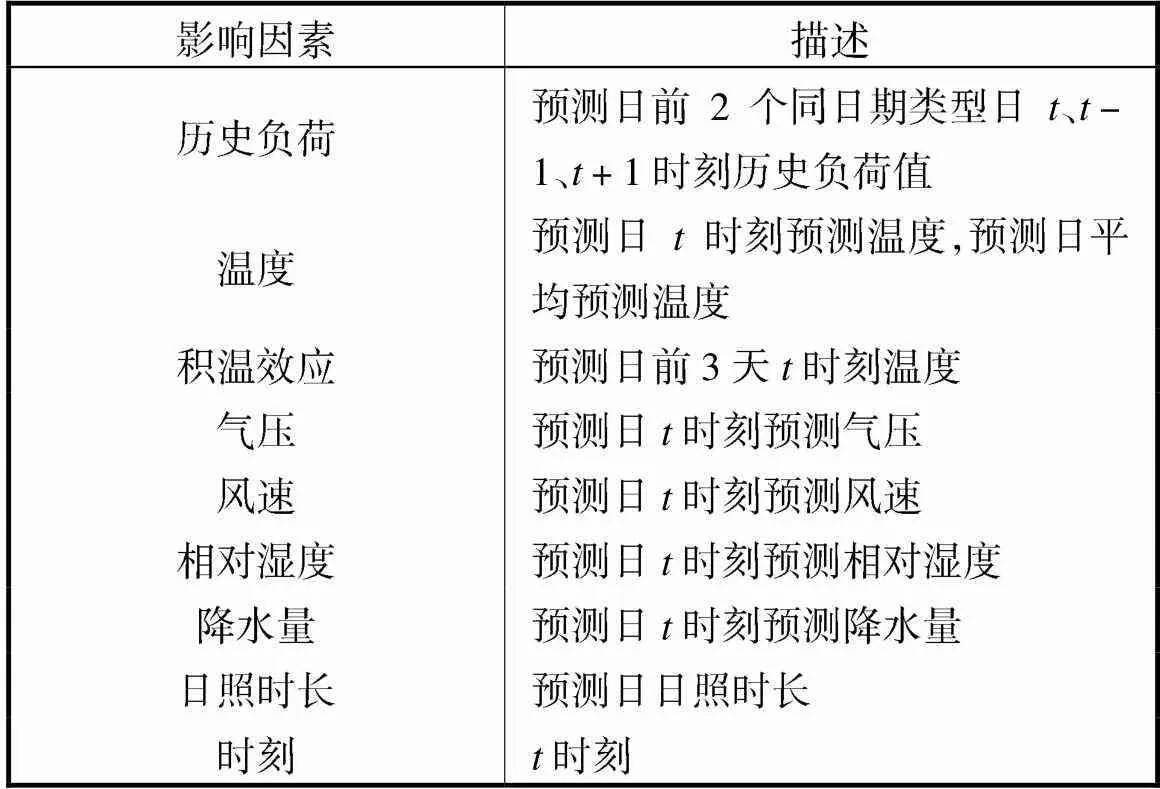
Tab.1 Input feature of load forecasting

1.2 负荷预测输入特征的筛选与降维

商业和居民混合负荷受到众多复杂因素的影响. 如果选取负荷预测输入特征过多，会导致预测模型出现过拟合现象，增加计算的复杂程度、降低模型性能．同时，商业和居民混合负荷具有较多气象输入特征，不同气象输入特征之间具有强相关性．为此，本文采用MIC法和FA法对气象输入特征进行降维，以降低负荷预测复杂程度．

1.2.1 最大信息系数法

针对商业和居民混合负荷预测和输入特征的强非线性特点，本文采用MIC法量化短期负荷与输入特征之间的关系，该方法能够公平覆盖所有类型函数，能较好克服原始数据中的噪声和异常点[9]，下面进行详细阐述．

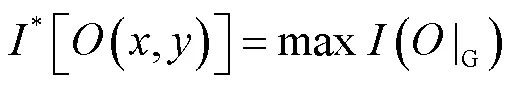
进一步，将其得到的互信息标准化，并求出最大互信息系数

两个变量之间的MIC值越大，其相关性越强；MIC值越小，相关性越弱．

1.2.2 因子分析法

因子分析法是一种通过降维技术化简多维向量的多元统计方法，属于主成分分析(principal component analysis，PCA)的推广，常被用于电力系统中具有复杂相关性的多维向量降维化简[10]．

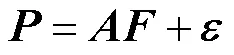
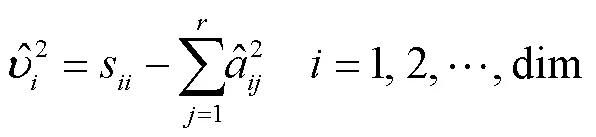
2 短期电力负荷预测方法

LSTMN预测方法是近年来一种典型的配电网负荷预测方法，其隐藏层神经元的个数选择步骤繁琐，同时针对不同的场景，达到最优预测效果所需要的神经元个数也不相同，寻优范围大，耗费时间长．本文利用灰狼优化算法(grey wolf optimization algorithm，GWOA)全局搜索能力强、收敛速度快的特点，进行隐藏层神经元的个数优化选取，可以在保证寻优速度的前提下，找到一个较好的LSTMN模型隐藏层神经元的个数，提高预测精度．

GWOA与郊狼优化算法(coyote optimization algorithm，COA)同属狼群算法，但是结构上较COA简洁，实现简易，效果明朗，同时较COA在算法的收敛速度、运算效率方面更为出色．郊狼算法独特的搜索方式与结构，较好地平衡了算法的探索与开发能力. 通过分组更新候选解的方式，显著提高了获得最优解的概率，但COA由于提出的时间较短，各方面仍需要完善，如在处理某些复杂优化问题时存在处理时间长、收敛速度慢的问题．另外，在郊狼的成长阶段，采用贪心算法判断是否保留新解的方式虽然在一定程度上加快了算法收敛速度，但是也进一步提高了陷入局部最优的概率．

LSTMN预测模型一次训练所选取的样本数在不同的场景下可以有一定的预估范围，这样有效回避了COA容易陷入局部最优、处理时间长、收敛速度慢的缺点，突出COA强大的局部搜索能力，因此，通过将两者的优点结合，提出了一种HGWOACOA，进行LSTMN预测模型优化，利用COA对LSTMN预测模型一次训练的样本数进行优化选取，以均方根误差(RMSE)作为郊狼的适应度，通过迭代最终选取最优解，在预估范围内实现全局优化．在降低复杂程度的同时，提高运算效率，提升优化性能．

2.1 长短时记忆网络

LSTMN是基于循环神经网络(recurrent neural network，RNN)的一种改进算法[11-13]．它解决了传统RNN循环神经网络梯度反转过程中由于逐步缩减而产生的梯度消失的问题，同时又能够很好地解释预测对象和多个影响因素之间的复杂非线性关系，适用于对影响因素众多且具有复杂随机性的商业和居民混合负荷进行预测．

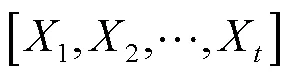
图1 LSTMN的内部结构

LSTMN的训练过程分为前向传播和反向传播两个阶段．前向传播通过式(9)～式(14)计算出神经元的输出值；反向传播采用的是基于时间的反向传播(back propagation through time，BPTT)算法，通过反向计算每个神经元的误差，进而根据误差去优化神经元的权重．相较于其他模型优化算法，Adam梯度下降算法具有计算高效平稳、占用内存较少且较好处理稀疏梯度的特点，因此，本文用其来优化参数的自适应学习率．

在LSTMN模型中，隐藏层神经元个数选择以及一次训练所选取的样本数是其两个重要参数，对模型的预测性能有较大的影响．

在隐藏层神经元个数选择方面，如果隐藏层神经元的数目过少，模型的训练效果就会很差，模型的泛化能力弱，甚至完全没有实用价值；如果隐藏层神经元的数目过多，则会在训练过程中出现过拟合的现象，对实验结果的精确性造成影响．

在一次训练所选取的样本数方面，样本数(bath size)的大小直接影响模型的优化性能，如果选取了适当的样本数，梯度下降的方向会更加准确．本文通过采用灰狼郊狼混合优化算法对LSTMN进行参数寻优，以提高LSTMN预测模型的精度．

2.2 灰狼优化算法

GWOA是在2014年由Mirgalili等[14]提出的一种种群智能优化搜索算法．该算法模拟灰狼群体中的社会等级支配关系以及搜寻、包围、攻击猎物等一系列机制来完成对参数的优化工作．一般而言，GWOA在全局寻优方面的效果要优于遗传算法(genetic algorithm，GA)、粒子群算法(particle swarm optimization，PSO)等智能优化算法．同时，该算法具有较强的收敛性能，参数简单且易于实现．GWOA中的灰狼群等级制度如图2所示．

图2 灰狼群等级制度

(1) 狩猎距离．狼群进行狩猎前，首先要对猎物进行包围，确定灰狼群与猎物之间的距离

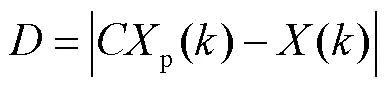
(2) 狼群位置的更新．在对猎物进行包围，确定狼群与猎物之间的距离后，需要对灰狼自身的位置进行更新，其更新公式为

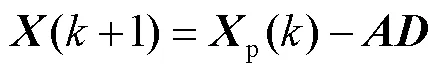
式中为收敛因子，表达式为

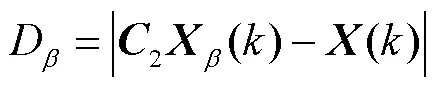
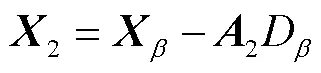
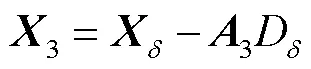
2.3 郊狼优化算法

COA是由Pierezan等[15]在2018年提出的一种新型智能算法．COA模拟郊狼的成长、生老病死、被驱逐和被接纳等一系列社会活动．在结构上采用多组搜索框架，具有极强的全局探索能力，同时组内采用的引导新生郊狼的成长方式对局部探索能力有了一定的加强，能够更好地解决复杂优化问题．COA包括初始化狼群和随机分组、组内郊狼成长、郊狼生与死、被组群驱逐接纳等主要步骤．

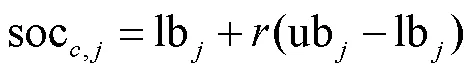
然后，再对郊狼的社会适应度fit进行计算，即

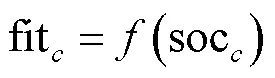
最后通过迭代贪心算法迭代，选取最优狼

(3) 郊狼生与死．在COA中，郊狼的重要社会活动是郊狼的出生与死亡．新郊狼的出生来自于父母郊狼的遗传和环境的变异，新郊狼出生后对其社会适应度进行评估．若组内只有一只郊狼比年幼郊狼的社会适应度低，则淘汰社会适应能力差的郊狼，幼狼得以存活；若组内存在多个社会适应度低于幼狼的郊狼，则从中选取年龄最大的那只淘汰，如果存在多个年龄最大的郊狼，则其中最差的郊狼淘汰，幼狼存活；若幼狼的社会适应度低于全组郊狼，则幼狼淘汰．一系列社会活动的模型为

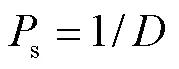
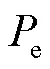
2.4 预测模型的建立与算法流程

本文针对商业和居民的混合配电网短期负荷预测制约因素多、强随机性的特点，提出的基于HGWOACOA-LSTMN的配电网短期电力负荷预测模型主要步骤如下．

(1) 数据的分析与预处理．

(2) 采用MIC和FA算法对气象输入特征中的主要信息进行提取，实现输入特征的筛选与降维．

(3) 选取相似日构成模型训练样本；相似日日平均温度与预测日相差±3℃以内且日期类型(休息日、工作日)与预测日一致的样本组合成相似日集．

(4) 训练样本集．将训练样本集选取预测日的负荷数据作为测试集，其余部分按照对应数据集的比例作为训练集，以LSTMN模型的均方根误差作为HGWOACOA的适应度函数，对LSTMN的参数进行寻优，首先郊狼优化算法先对LSTMN模型一次训练所选取的样本数进行优化选取，然后灰狼优化算法对LSTMN模型的隐藏层神经元的个数进行优化选取，实现LSTMN模型两类参数的优化．

(5) 输入训练样本集对最优参数LSTMN短期负荷预测模型进行离线训练，得到基于HGWOACOA-LSTMN的短期电力负荷预测模型．最后将预测日的输入特征数据输入预测模型中，得到预测日各个时刻的负荷预测值．算法流程如图3所示．

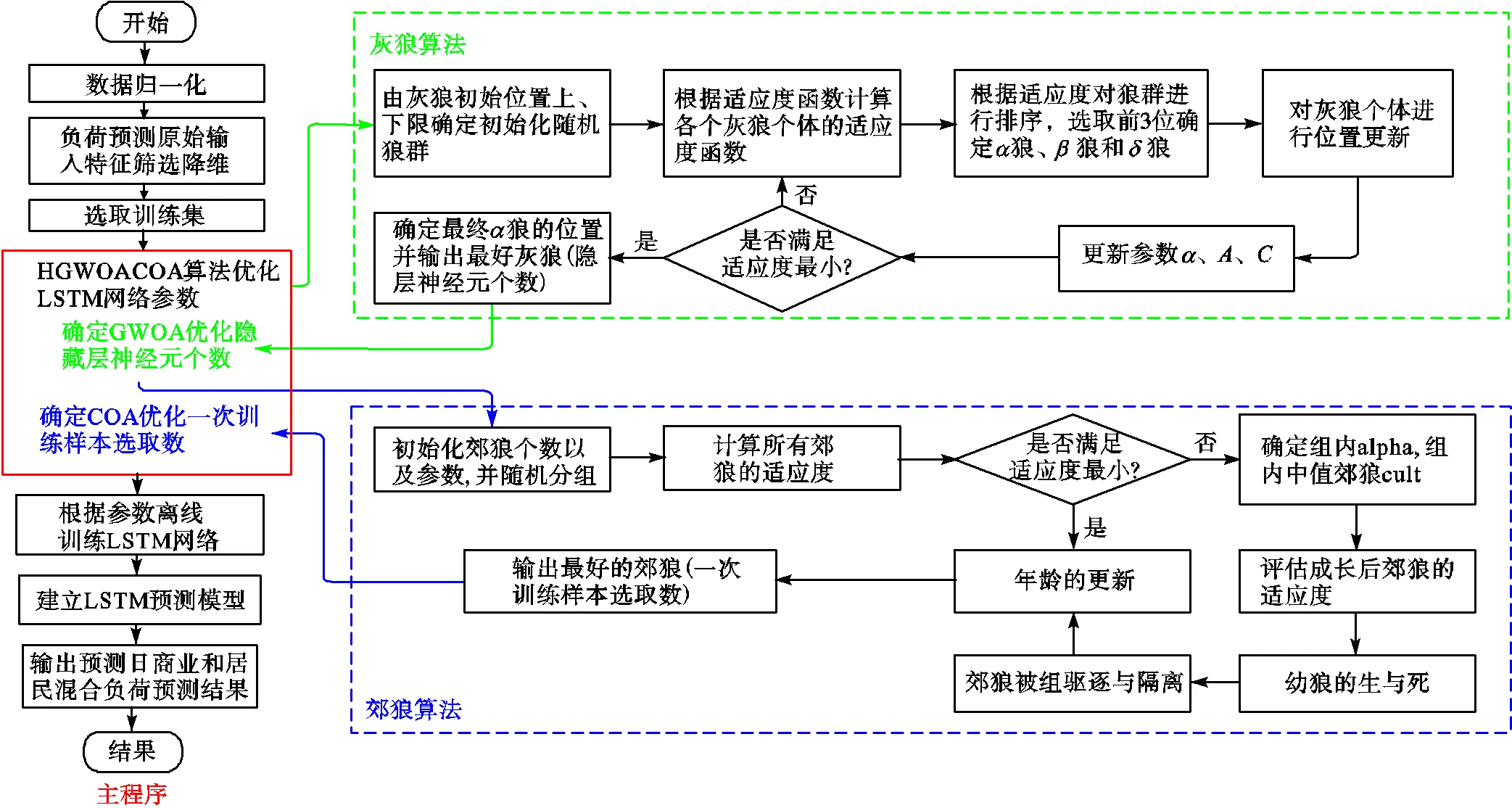
图3 基于HGWOACOA-LSTMN的短期电力负荷预测流程

3 短期负荷预测实例及结果分析

本文以配电网某区域(包含一座商业综合体和两个居民小区)2016年12月1日至2017年11月30日的负荷数据为例验证本文方法的有效性，其中负荷数据采集的时间间隔为1h．

3.1 误差指标

本文采用平均绝对百分比误差(MAPE)、均方根误差(RMSE)来衡量预测模型的准确性与鲁棒性，计算方法分别如式(38)、式(39)所示．MAPE表示预测结果较实际结果的数据偏移程度，计算MAPE可以评价模型预测误差的波动程度；RMSE对误差结果中极大或极小的值反应敏感，计算RMSE可以检验模型的拟合水平和稳定性．

3.2 数据归一化

为了提升模型的收敛速度，保证模型的精度，对历史负荷和输入特征数据进行归一化处理，按式(40)将输入特征数据映射到[1，-1]区间上．

3.3 原始输入特征的筛选与降维

本文首先采用最大信息系数(MIC)法对气象输入特征进行筛选．文献[10]认为在显著性水平为0.001时，MIC＝0.28，即当MIC＞0.28时，可认为外部影响因素与负荷具有显著性关系．通过MIC对表1列出的9项20种原始输入特征与商业和居民混合负荷的相关性进行分析，可得相对湿度、风速与降水量的MIC相关性值分别为0.13、0.11和0.09，均小于MIC规定的阈值0.28，因此，可将相对湿度、风速与降水量这3项输入特征剔除．

根据因子得分系数可构成公因子的线性函数方程．可以得出：从气象输入特征中提取出公因子，公因子的方差贡献率为94.079%(＞85%)，说明该公因子已基本包含10项气象输入特征的全部有效信息，见表2．

表2 气象输入特征的因子分析结果

Tab.2 Factor analysis results of meteorological input characteristics

3.4 预测结果分析

优化前LSTMN模型的参数与优化后LSTMN模型的参数如表3所示，模型训练过程loss曲线如图4、图5所示，通过loss曲线可以较为直观地反映出该模型训练的情况，侧面反映参数优化前后模型的性能优劣，负荷实际与预测值如表4所示，两模型预测结果中实际值与预测值误差对比如图6所示．

表3 传统LSTMN与HGWOACOA-LSTMN模型参数选择

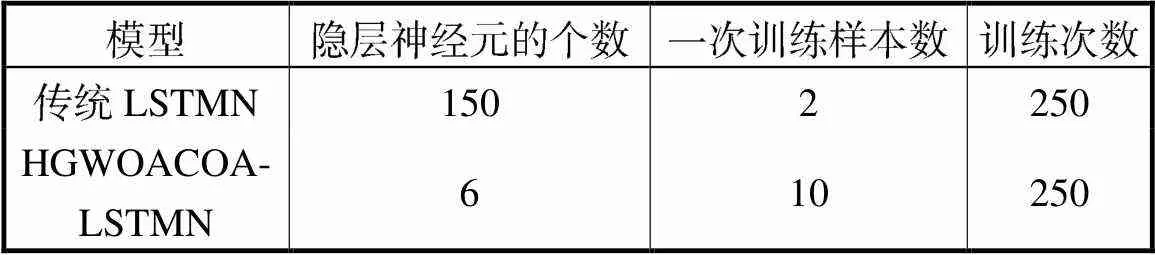
Tab.3 Parameter selection of traditional LSTMN model and HGWOACOA-LSTMN model

表4 传统LSTMN与HGWOACOA-LSTMN模型预测负荷比较

Tab.4 Comparison of traditional LSTMN model and HGWOACOA-LSTMN model for load forecasting

通过分析上述图表，可以得出以下结论．

(1)从图4、图5可知，当训练次数设置为250次时，两模型训练集和测试集损失值曲线不断下降直至趋于平稳，表明两模型的训练过程良好，但HGWOACOA-LSTMN模型较传统LSTMN模型在训练集loss与测试集loss之间的偏差更小，同时曲线变化更为平稳，拟合程度更好，说明把GWOA以及COA寻优得到的参数输入模型后，模型训练效果得到了改善．

(2)由图6可以看出，HGWOACOA-LSTMN模型的预测误差比传统LSTMN模型有了明显的降低，而且HGWOACOA-LSTMN模型能够把大部分的预测误差控制在6%以内．

图6 传统LSTMN与HGWOACOA-LSTMN模型预测误差

(3)由图6和表4可以看到，在部分时刻，传统LSTMN模型的实际负荷与预测负荷偏差较大，预测精度难以保证．相比于传统LSTMN模型，本文提出的模型鲁棒性更好，更加符合短时电力负荷预测精准与稳定的要求．

为了验证本文提出的面向商业与居民混合的配电网电力负荷预测模型的精确性，分别选取春、夏、秋、冬4个季节进行预测，与基于RBFNN算法、传统LSTMN算法的预测模型进行实验对比，其中，RBFNN算法的优化参数光滑因子采用网格搜索法获得，预测结果如表5所示．同时为了进一步验证模型的泛化性，保证模型在处理多段复杂时间序列负荷数据时的准确性，依次选取冬季训练集中的某几个典型日作为预测数据，结果如图7所示．

表5 不同季节3种预测模型精度比较

Tab.5 Comparison of the accuracy of three prediction models in different seasons

由实验结果可以得到如下结论．

(1) 总体来看，由表5可知，HGWOACOA-LSTMN的MAPE和RMSE四季平均值均小于对比模型．在夏冬两季相较于LSTMN和RBFNN来说同样误差较小，在春秋两季，传统LSTMN模型与HGWOACOA-LSTMN模型的RMSE无明显差异，但MAPE高了很多，说明传统LSTMN模型的鲁棒性相对较弱．同时，HGWOACOA-LSTMN模型的MAPE均值较其余两种模型分别降低了0.99%和3.44%；RMSE的均值为69.17，较传统的LSTMN模型和RBFNN分别降低了20.60和16.56，表明本文提出的短时电力负荷HGWOACOA-LSTMN预测模型在预测过程中具有较强的精确度与鲁棒性，该模型能更好地拟合商业和居民混合负荷与输入特征之间的复杂非线性关系，具有较强的抗干扰能力．

图7 不同个数典型日下预测误差

(2) 由图7可以看到，在连续日的预测中，HGWOACOA-LSTMN模型能够把绝大部分误差控制在10%以内，且负荷预测误差较为稳定，表明HGWOACOA-LATM短时负荷预测模型在处理复杂时间序列预测问题时具有极强的泛化性．

3.5 优化方法对比分析

为了进一步验证HGWOACOA-LSTMN模型的优化效果，本文选取了春、冬两季商业和居民混合负荷历史数据，分别将GWOA、COA、HGWOACOA共3种模型对LSMTN进行参数优化，比较其优化后LSTMN模型的精度与速度，参数选择如表6所示，其中COA-LSTMN代表LSTMN模型只进行郊狼优化算法对一次训练选取样本数参数优化，GWOA-LSTMN代表LSTMN模型代表只进行灰狼优化算法对隐层神经元个数参数优化，运算结果如表7所示．

表6 不同模型的优化参数选择

Tab.6 Optimization parameter selection of different models

表7 不同模型的优化效果对比

Tab.7 Optimization effect comparison of different models

由表7中春季和冬季的实验结果可知，只通过GWO对隐层神经元个数优化，评估指标RMSE、MAPE变化范围很小，但在运行时间上较传统LSTMN负荷预测模型分别减少了34.65s和112.54s．只通过COA对LSTMN一次训练选取样本数进行参数优化，优化后的预测模型较传统LSTMN负荷预测模型的RMSE、MAPE显著下降，但在运行时间上较传统LSTMN分别减少了54.87s与7.63s，这表明只通过COA进行一次训练选取样本数参数优化模型的运行速度虽然有所提高，但具有一定的不确定性，稳定性较差．

由表7中还可以看到，通过将GWOA、COA算法结合对LSTMN进行参数优化，较传统LSTMN负荷预测模型RMSE、MAPE、模型的运行时间都有着显著提升．因此，相对于GWOA、COA算法单方面的参数优化，HGWOACOA优化算法在考虑模型的预测精度的同时，保证了模型的运行速度，显著提高了负荷预测效率和准确性．

4 结 论

(1) 考虑负荷历史数据、气象因素和日期类型3方面构建负荷预测输入特征，分别采用MIC和FA方法对气象输入特征进行筛选与降维，提取出含有原始信息90%以上的较少变量，在保证精度的前提下，简化了模型输入特征的维数．

(2) HGWOACOA-LSTMN模型能较好地拟合商业和居民混合的配电网负荷与输入特征之间的复杂非线性关系，在处理时间序列问题时较其他模型更加具优势．利用GWOA、COA各自的优势分别对隐层神经元个数与一次训练选取样本数进行优化，弥补参数选择时的困难，保证预测精度的同时进一步提升运行效率与其拟合回归的能力．

(3) 本文模型充分挖掘历史负荷与气象因素中的有效信息，具有较好的鲁棒性及较高的预测精度，可为今后包含商业和居民混合的配电网短期电力负荷预测研究提供借鉴．

［1］ 史佳琪，张建华. 基于多模型融合Stacking 集成学习方式的负荷预测方法[J]. 中国电机工程学报，2019，39(14)：4032-4041.

Shi Jiaqi，Zhang Jianhua. Load forecasting based on multi-model by Stacking ensemble learning[J]. Proceedings of the CSEE，2019，39(14)：4032-4041(in Chinese).

［2］ 杨 阳，练 冲，马 超. 晴天光伏发电功率的日内变化规律及预测方法研究[J]. 天津大学学报：自然科学与工程技术版，2020，53(6)：565-572.

Yang Yang，Lian Chong，Ma Chao. Daily variation laws and prediction methods in photovoltaic power generation on sunny days[J]. Journal of Tianjin University：Science and Technology，2020，53(6)：565-572(in Chinese).

［3］ 陆继翔，张琪培，杨志宏，等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化，2019，43(8)：131-137.

Lu Jixiang，Zhang Qipei，Yang Zhihong，et al. Short-term load forecasting method based on CNN-LSTM hybrid neural network medol[J]. Automation of Electric Power Systems，2019，43(8)：131-137(in Chinese).

［4］ 彭 文，王金睿，尹山青. 电力市场中基于 Attention-LSTM 的短期负荷预测模型[J]. 电网技术，2019，43(5)：1745-1751.

Peng Wen，Wang Jinrui，Yin Shanqing. Short-term load forecasting model based on Attention-LSTM in electricity market[J]. Power System Technology，2019，43(5)：1745-1751(in Chinese).

［5］ 张素香，赵丙镇，王风雨，等. 海量数据下的电力负荷短期预测[J]. 中国电机工程学报，2015，35(1)：2805-2813.

Zhang Suxiang，Zhao Bingzhen，Wang Fengyu，et al. Short-term power load forecasting based on big data [J]. Proceedings of the CSEE，2015，35(1)：2805-2813(in Chinese).

［6］ Chau Tat Kei，Yu Samson Shenglong，Fernando Tyrone，et al. A load-forecasting-based adaptive parameter optimization strategy of STATCOM using ANNs for enhancement of LFOD in power systems[J]. IEEE Transactions on Industrial Informatics，2018，14(6)：2463-2472.

［7］ 杨屹洲，方瑞明，黄文权，等. 应用小波变换和支持向量机的商业电力负荷预测[J]. 华侨大学学报：自然科学版，2015，36(2)：142-146.

Yang Yizhou，Fang Ruiming，Huang Wenquan，et al. Commercial power load forecasting using wavelet transform and SVM[J]. Journal of Huaqiao University：Natural Science，2015，36(2)：142-146(in Chinese).

［8］ 李冬辉，尹海燕，郑博文．基于MFOA-GRNN模型的年电力负荷预测[J]. 电网技术，2018，42(2)：585-590．

Li Donghui，Yin Haiyan，Zheng Bowen．An annual load forecasting model based on generalized regression neural network with multi-swarm fruit fly optimization algorithm[J]. Power System Technology，2018，42(2)：585-590(in Chinese)．

［9］ 蒋杭进. 最大信息系数及其在脑网络分析中的应用[D]. 武汉，中国科学院研究生院(武汉物理与数学研究所)，2013.

Jiang Hangjin. Maximal Information Coefficient and Its Application to Brain Network Analysis[D]. Wuhan：Graduate School of Chinese Academy of Sciences(Wuhan Institute of Physicsand Mathematics)，2013(in Chinese).

［10］ 张冠英，羡一鸣，葛磊蛟，等．经济新常态下基于 Verhulst-SVM 的中长期负荷预测模型[J]. 电测与仪表，2019，56(1)：102-107．

Zhang Guanying，Xian Yiming，Ge Leijiao，et al. Medium and long-term load forecasting model based on Verhulst-SVM under new normal economy[J]. Electrical Measurement & Instrumentation，2019，56(1)：102-107(in Chinese).

［11］ Hochreiter S，Schmidhuber J. Long short-term memory[J]. Neural Computation，1997，9(8)：1735-1780.

［12］ Zhang Y Z，Xiong R，He H W，et al. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries[J]. IEEE Transactions on Vehicular Technology，2018，67(7)：5695-5705.

［13］ Peng T M，Hubele N F，Karady G G. Advancement in the application of neural networks for short-term load forecasting[J]. IEEE Transactions on Power Systems，1992，7(1)：250-257.

［14］ Mirjalili S，Mirjalili S.M，Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software，2014，69：46-61.

［15］ Pierezan J，Coelho L S. Coyote optimization algorithm: A new metaheuristic for global optimization problems[C]// 2018 IEEE Congress on Evolutionary Computation(CEC). Rio de Janeiro，Brazil，2018：2633-2640.

An HGWOACOA-LSTMN Method for Short-Term Load Forecasting of Distribution Network for Commercial and Residential Users

Ge Leijiao1，Liu Hangxu1，Zhao Kang2，Li Hua3，Zhang Bo4，Li Yuanliang1

(1. Key Laboratory of Smart Grid of Ministry of Education，Tianjin University，Tianjin 300072，China；2. School of Electrical and Automation Engineering，Shandong University of Science and Technology，Qingdao 266590，China；3. Economic and Technological Research Institute，State Grid Liaoning Electric Power Co.，Ltd.，Shenyang 110015，China；4.32654 PLA Troops，Jinan 250024，China)

For the commercial and residential mixed distribution network load forecasting，the influence factors are diverse and randomness is high. A short-term power load forecasting method of distribuion network based on the hydrid grey wolf optimization algorithm with coyote optimization algorithm(HGWOACOA) and long short-term memory network (LSTMN)is proposed. To select and reduce multiple input characteristics of power load，in this paper，we use the maximum information coefficient(MIC) method to quantify the nonlinear correlation between the load and input characteristics，eliminate the invalid features，and then use the factor analysis(FA) method to extract the information of historical data，meteorology，temperature and other input features，so as to reduce the dimension of effective influencing factors. Results show that the grey wolf optimization algorithm(GWOA) has strong global search ability and fast convergence speed，and the coyote optimization algorithm(COA) has strong global search ability and fast convergence speed. To highlight the advantages of the two algorithms and make up for their corresponding shortcomings，a hybrid GWOA with COA(HGWOACOA)is proposed to solve long short-term memory networks. The number of hidden layer neurons and the number of training samples are optimized to overcome the difficulty of parameter selection. While ensuring the prediction accuracy，the operation efficiency is also improved，which realized the high-precision short-term power load forecasting of the distribution network based on HGWOACOA-LSTMN. Taking a commercial and residential mixed load in a distribution network as an example，the accuracy and robustness of the proposed forecasting method are verified. Meanwhile，the operation efficiency is improved and the dimension of  the input characteristics of the model is simplified，which proves the accuracy and applicability of the proposed method.

distribution network；short-term load forecasting；factor analysis；grey wolf optimization algorithm；coyote optimization algorithm；long short-term memory network

10.11784/tdxbz202103075

TM744

A

0493-2137(2021)12-1269-11

2021-03-31；

2021-06-03.

葛磊蛟（1984—  ），男，博士，副教授.Email：m_bigm@tju.edu.cn

葛磊蛟，legendglj99@tju.edu.cn.

国家自然科学基金资助项目(51807134)；省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学)开放课题基金资助项目(EERI_KF20200014).

the National Natural Science Foundation of China(No.51807134)，the State Key Laboratory of Reliability and Intelligence of Electrical Equipment，Hebei University of Technology(No.EERI_KF20200014).

(责任编辑：樊素英)