大跨度拱桥组合格构梁桥面板的抗疲劳性能研究

刘雪雷，张军辉

(广西交科集团有限公司，广西 南宁 530007)

0 引言

大跨度拱桥上部主要承重结构包括拱肋和桥面板。随着桥梁跨度的增大，其桥面板形式逐渐由混凝土结构发展为钢结构。而钢桥面板由于直接承受车辆荷载，在车辆反复压载作用下，容易产生疲劳微裂纹，然后逐步发展成为裂缝，直至结构破坏。这被称为桥面疲劳问题，一直是桥梁设计绕不开的难题。最有代表性的是英国的Severn桥，该桥在桥面板的纵肋、横隔板处均出现了不同程度的疲劳裂缝。国内关于大跨度桥梁的桥面结构出现疲劳问题也偶有报道。

为了克服桥面板的疲劳问题，工程师们从各个方面出发，探索了一系列处理方法，例如加厚桥面钢板、改变纵向U肋的焊接形式以及改善顶板的疲劳细节等，但成效有限。随着组合结构的发展，其抗疲劳效果好的特点为解决这类问题提供了一个新的方向。

一般的组合梁用于普通梁桥，其跨径就是桥梁跨径，不太适用于大跨度拱桥的桥面结构。组合格梁是组合梁的一种，由纵横交错的钢主梁和混凝土顶板组成，通过吊点或者支点形成多个连续小跨径，从而形成特别适用于大跨度拱桥的桥面结构，目前应用较多，发展较快。

1 组合格构桥面板的疲劳构造细节

疲劳构造细节也称疲劳细节，是决定结构的疲劳承载能力的关键所在。根据以往的工程经验以及规范中关于疲劳细节的规定，在组合格构梁上选取了6个疲劳细节：(1)主纵梁的纵向对接焊缝处，对应构造细节为A；(2)次纵梁的纵向对接焊缝处，对应构造细节为B；(3)主横梁的纵向对接焊缝处，对应构造细节为C；(4)次横梁的纵向对接焊缝处，对应构造细节为D；(5)主横梁与纵梁的交点处，对应构造细节为E；(6)次横梁与纵梁的交点处，对应构造细节为F。由于横梁是通长的，在交点处纵梁焊接于横梁上，因此不选取纵梁在横梁交点处的疲劳细节。具体的部位细节如图1所示。

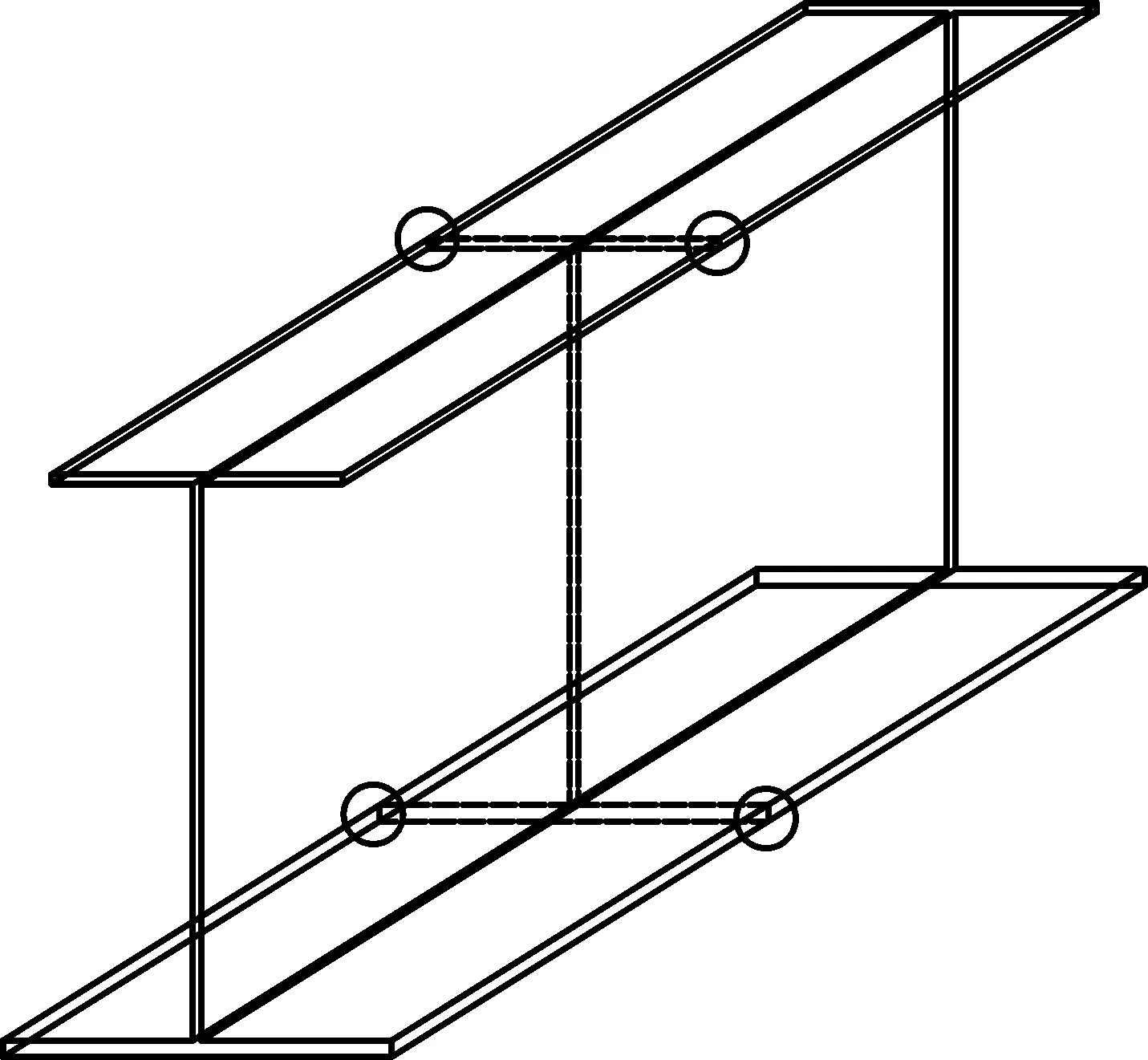
(a)细节(A/B/C/D)

2 理论计算模型

本文以正在设计过程中大跨钢管混凝土拱桥——环江四桥为工程背景，研究结果可用于指导桥梁设计。经过静力分析和设计后，该实桥钢-混凝土组合格构桥面板由C40混凝土顶板和Q355C低合金高强度结构钢的钢板梁组成，构件的几何参数如表1所示。

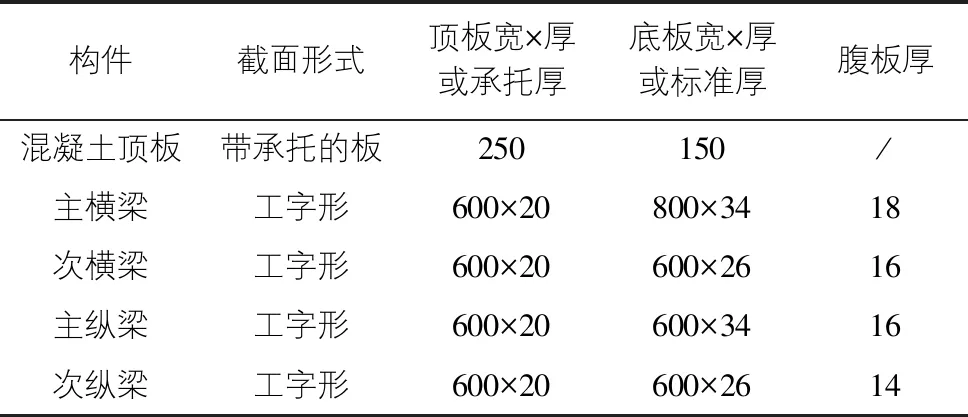
表1 组合格构桥面板的几何参数表(mm)

钢主梁设有两个纵向的主纵梁和若干个主横梁。主纵梁和主横梁的交叉点是吊杆或立柱的支点，其截面刚度较大。主纵梁为纵桥向，间距为26.1 m，其间设有三个中次纵梁，间距为6.525 m，并在两侧外悬臂7.25 m处各设一道次纵梁。主横梁间距为8 m，其间设有两个次横梁，次横梁间距为2.7 m。钢格构梁均为钢板梁，且均为直角相交。在钢格构梁上设钢筋混凝土板，其在承托部分板厚为25 cm，一般板厚为15 cm。桥面板通过剪力钉和PBL剪力键与钢格构梁形成了钢-混凝土组合格构梁。本文不考虑钢与混凝土的界面滑移效应。

通过Midas Civil建立有限元计算模型，其中工字钢梁以空间梁单元模拟，钢筋混凝土板以板单元模拟。由于吊杆和拱肋会对疲劳车辆荷载产生影响，因此建立了全桥的有限元分析模型，全桥共7 822个节点和9 978个单元，有限元模型如图2所示。

图2 全桥的有限元计算模型图

3 疲劳加载分析

《公路桥涵设计通用规范》(JTG D60-2015)[1]和《公路钢结构桥梁设计规范》(JTG D64-2015)[2]对于疲劳荷载的规定大致相同，疲劳荷载共三个计算模型Ⅰ～Ⅲ，同时规定，对于桥面系构件的验算，采用疲劳计算模型Ⅲ。疲劳计算模型Ⅲ的加载车辆如图3所示。

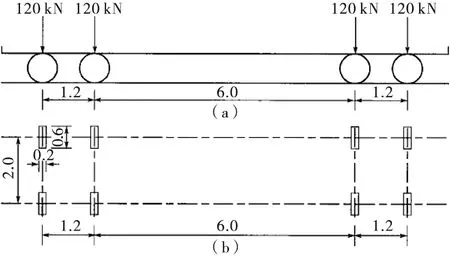
图3 疲劳计算模型Ⅲ的加载车辆示意图(m)

桥面沥青铺装不提供结构抗力，且沥青铺装弹性模型小，忽略其对汽车轮载扩散作用，因此分析组合梁混凝土桥面板时，车辆计算着力面积为0.6 m×0.2 m。但在分析钢梁的疲劳应力时，钢筋混凝土板刚度大，按经验值取45°的应力扩散角。扩散计算时，不考虑承托加厚部分，统一按15 cm厚考虑，因此分析钢梁时，车辆计算着力面积为0.9 m×0.5 m。车辆轮载按压力荷载加载。

4 疲劳的参数分析与对比

根据有限元加载分析计算结果，提出了各个疲劳细节的疲劳应力幅，如表2所示。

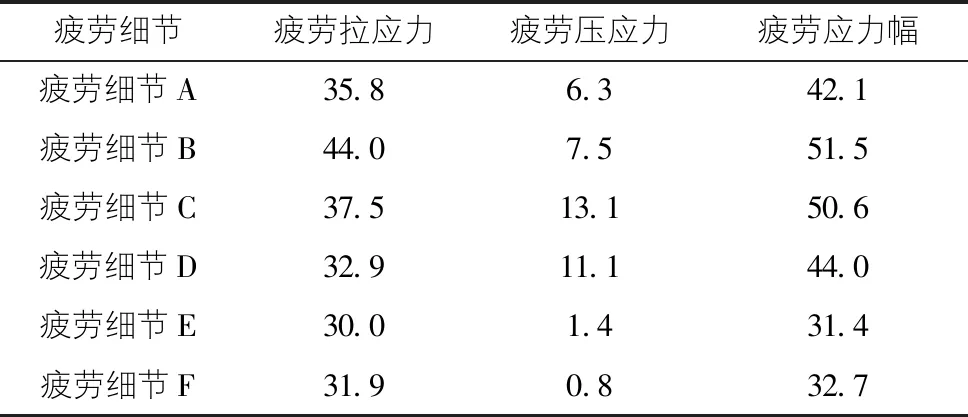
表2 有限元计算的构件疲劳应力幅数值表(MPa)

S-N曲线是指构件疲劳应力幅与构件疲劳寿命之间关系的曲线，其中疲劳寿命以循环次数表示。由于疲劳寿命跨度大，工程一般以疲劳寿命的对数为横坐标，对应地以疲劳应力幅为纵坐标绘制S-N曲线，如图4所示。S-N曲线分为三段，第一段和第二段分别为斜率为1/3和2/3的斜直线，第三段为水平直线。根据规范，疲劳寿命Nc为200万次时所对应的应力幅为疲劳细节类别ΔσC，疲劳寿命Nc为500万次时所对应的应力幅为常幅疲劳极限ΔσD，疲劳寿命Nc为1亿次时所对应的应力幅为截止限ΔσL。

图4 正应力幅疲劳强度曲线图

斜直线段满足以下关系式：

logN=logC-mlogσ

(1)

式中：C——与材料相关的常数；

m——S-N曲线的负倒数，在第一段取值为3，第二段取值为5。

当轮载作用下构造细节的最大应力幅Δσmax满足式(2)时，认为结构不会发生疲劳破坏，不需要对其进行疲劳损伤评估；当应力幅中低于疲劳截止限ΔσL的应力循环不予考虑。

(2)

式中：γMf——构件的疲劳抗力分项系数，对重要构件取1.35。

根据式(1)和式(2)，对S-N曲线进行扩充，可以得到新的S-N曲线方程组：

(3)

式中：γFf——构件的疲劳荷载分项系数，按规范取1.0。

根据疲劳细节查表并根据式(3)计算得到疲劳寿命的应力幅值，如表3所示。

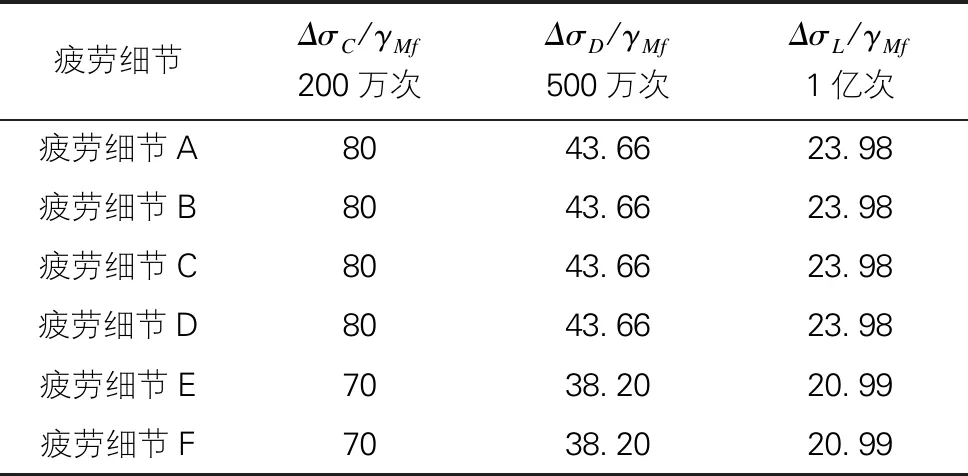
表3 疲劳寿命对应的应力幅值表(MPa)

根据式(3)，对疲劳细节A～D进行S-N曲线扩展，得到下列的疲劳细节A～D的S-N曲线方程。

(4)

根据有限元的计算结果，疲劳细节A的应力幅小于表3中的ΔσD/γMf=43.66 MPa，疲劳寿命无穷大；而疲劳细节B～D的应力幅均大于该值。疲劳细节B的应力幅为51.5 MPa，则由式(4)可以计算得出疲劳细节B的疲劳寿命NB=3.56×1015/(ΔσB)3=9.8×106。同理可计算出其他疲劳细节的寿命，列出如下：

根据计算结果，疲劳细节A～D的寿命均超过了常幅疲劳极限的500万次，结构不会发生疲劳损伤。

同样地，根据式(3)，对疲劳细节E～F进行S-N曲线扩展，得到下列的疲劳细节E～F的S-N曲线方程：

(5)

根据有限元的计算结果，疲劳细节E、F的应力幅分别为31.4 MPa和32.7 MPa，均小于表3中的ΔσD/γMf=38.2 MPa，疲劳寿命无穷大。列出如下：

由此可见，疲劳细节E～F也不会发生疲劳损伤。

5 结语

根据计算和分析结果，所有选定的疲劳细节的寿命均满足规范要求，最小的疲劳寿命发生在次纵梁的纵向对接焊缝处(疲劳细节B)，为9.8×106次，远大于常幅疲劳极限的5×106次，明显大于一般的纯钢桥面板[3]，充分体现了钢-混凝土组合格构梁在抗疲劳方面的独特优势。分析原因，主要可归纳为以下三个方面：

(1)混凝土材料由于厚度远大于钢材，其应力幅度相对较小。在结构设计验算时，钢材的设计计算应力一般为200 MPa左右，而混凝土则为10～30 MPa，这也是混凝土结构可以不考虑疲劳损伤的原因。当形成组合结构时，会使组合结构钢材的疲劳应力幅明显减少。

(2)组合结构的混凝土顶板厚度远大于纯钢结构的钢顶板，能够使车轮荷载均匀扩散，大幅减少了荷载的集中度，从而减少了疲劳应力幅[4]。以本桥为例，15 cm厚的混凝土顶板，按45°扩散角考虑，可增加42%的受力面积。而纯钢顶板厚度为16 mm，几乎不考虑应力的扩散。

(3)钢-混凝土组合格构梁由钢板梁和混凝顶板构成，顶板无加劲肋，钢结构为工字形的钢板梁，疲劳细节好。根据前文提取的疲劳细节，本结构的钢梁疲劳细节为80 MPa和70 MPa。而纯钢梁的控制疲劳细节为顶板U肋和钢横隔板，其构造细节为50 MPa和55 MPa，这会使钢-混凝土组合格构梁有较好的疲劳抗力，因而具有更长的疲劳寿命。

本文针对抗疲劳性能对钢-混凝土组合格构梁进行了研究，结果既可以用来指导依托工程桥梁的设计，也对这种新式结构的发展提供指导意义。相对于成熟的钢格构桥面板或者钢筋混凝土桥面板，钢-混凝土组合格构梁桥面板还处于起步阶段，研究其疲劳性能和其他力学性能并开展试验和理论研究将是下一阶段工作的重点。