纳米孔道中磁场调控的离子输运特性

瞿忍婕，毛朝武，张振坤，曹留烜

(厦门大学能源学院，福建 厦门 361102)

纳米孔道在能量转换[1-2]、能源节约[3-4]和能量回收[5-6]等领域已有大量的报道.研究发现纳米孔道内表面与离子之间的相互作用很大程度上影响着能量转化效率[7-10].因此，探究纳米孔道内部界面的物理化学性质对能量的高效利用有着深远的影响.

通过改变纳米孔道的外环境可以提升离子在孔道内部的输运情况，例如施加电场[11-15]、液压[16]、温度梯度[17-18]、调节溶液的pH值[19]以及其他化学环境[20]等.Hou等[21]将铁粉与聚二甲基硅氧烷(PDMS)的混合物附着在薄膜的外表面上，通过磁场以快速、非接触的方式控制离子电流以及整流能力和电导率；外部磁场充当施加的机械力使锥形纳米孔道发生一定程度的形变，获得不同程度的门控效果.Park等[22]通过微机电系统(MEMS)技术，在Si3N4膜上刻蚀形成纳米孔，研究在不均匀磁场中磁性纳米颗粒通过固态纳米孔移位的性质，通过测量和分析离子电流阻滞，发现通过纳米孔道的纳米颗粒的移位速度与单个磁性纳米颗粒的磁化强度呈线性正相关.然而，迄今为止有关磁场对离子输运的调控在纳米多孔膜领域内的研究甚少.

本研究主要分析了纳米孔道中磁场调控离子输运的特性.在纳米多孔膜浓度梯度驱动发电的基础上，引入磁场来控制离子的输运.通过实验和模拟的对比验证，发现两者具有相同的变化趋势.进一步通过模拟，发现磁场可以有效地控制净扩散电流大小；并且可通过磁场调控离子输运用于分离不同价态的离子，在盐湖卤水提锂、核废料处理等领域具有一定的潜在应用价值.

1 实验部分

1.1 试剂与材料

少层Ti3C2Tx(MXene)纳米片分散液购自南京纳米先丰公司；KCl为分析纯，购自国药集团化学试剂有限公司；纤维素酯底膜购自上海利根商贸有限公司；去离子水、Ag/AgCl电极和聚四氟乙烯溶液槽均为自制.

1.2 仪器设备

超声细胞粉碎机(BILONG92-IIDL，上海比朗仪器制造有限公司)，超纯水系统(Milli-Q Synthesis，美国Millipore公司)，数字源表(Keithley 2400，美国吉利时公司)，场发射扫描电子显微镜(SEM,Zeiss SUPRA 55，德国Carl Zeiss AG 公司).

1.3 MXene薄膜的制备

先量取质量浓度为2.5 mg/mL的MXene分散液，将其稀释至0.1 mg/mL，使用超声细胞粉碎机粉碎后得到分散均匀的MXene分散液.然后取一定量的MXene分散液于纤维素酯底膜上，利用循环水式真空泵抽去其中的去离子水，如图1(a)所示，得到自下而上堆叠在底膜上的MXene纳米片，待观察不到明显水分时，将MXene膜小心取出.最后将其放入60 ℃ 真空烘箱中1 h左右，除去膜中多余的水，得到干燥且纳米片层堆叠排布的MXene膜.通过控制加入的分散液体积，可以得到厚度为100～3 000 nm的MXene薄膜，通过场发射SEM观察得到如图1(b)所示的微观结构，MXene膜的厚度约为2.03 μm，可以明显看到MXene膜的层状堆叠排布结构.

图1 采用真空抽滤法制备MXene层状堆叠膜(a)及其SEM截面图(b)

1.4 浓度梯度驱动的纳米多孔膜系统

在两个聚四氟乙烯溶液池之间夹一片MXene膜，再用一次性针筒将不同浓度的电解质溶液分别注射到两个溶液池中，两个溶液池之间通过纳米多孔膜进行物质输运.然后，在两边溶液池中插入一对Ag/AgCl电极，并保持两个电极与膜的距离相同，以提高实验结果的准确性.选择数字源表的电流扫描模式，得到不同浓度梯度下的扩散电流.这些纳米片的表面存在丰富的化学基团，如羟基等，使其在水中显负电性，因此纳米片存在负表面电荷.在局域内，离子与纳米片的带电表面之间的静电相互作用使阳离子优先于阴离子迁移，该区域被称为双电荷层，因此在浓度梯度驱动的纳米流体系统中,会形成一个与溶液浓度梯度同方向的净扩散电流[23].当纳米片之间紧密排列，其层间距离小于或等于德拜长度时，较强的离子分离将导致双电荷层重叠[24]，从而进一步增强净扩散电流.

1.5 磁场中的物理模型

如图2所示，矩形条代表MXene纳米片，它们自下而上有序堆叠.阴阳离子沿着浓度梯度方向进行扩散，在双电荷层的作用下，它们的非对称输运产生了净扩散电流.在浓度梯度驱动的纳米流体系统中，外加垂直于纸面的磁场.离子受到洛伦兹力的作用而发生偏转，如图2放大部分的阴阳离子受力示意图所示，阳离子在洛伦兹力和双电荷层效应的共同作用下，会更多地向出口上端偏移，而阴离子则相反.当离子处于相同的流体和背景场时，其所受的洛伦兹力大小与电荷量成正比，这使得基于磁场调控的纳米孔道可用于分离混合溶液中不同价态的离子.

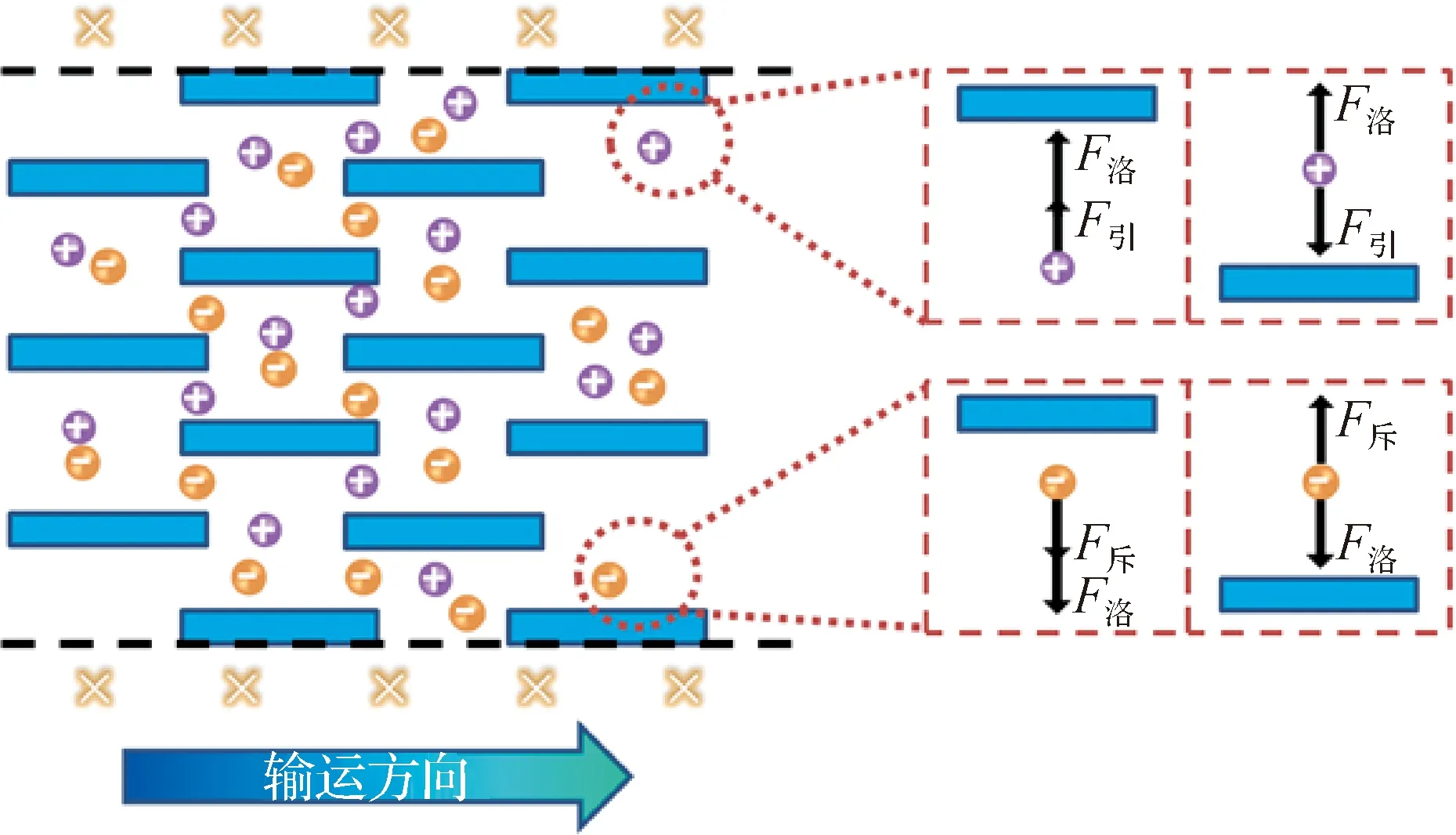
带负电的纳米片会吸引阳离子、排斥阴离子，垂直纸面向里的磁场使阴阳离子分别受到向下和向上的洛伦兹力.

1.6 数值计算方法

离子通过纳米孔道的输运计算主要采用PNP(Poisson and Nernst-Planck)方程[25]和附加的洛伦兹力方程：

(1)

(2)

Fi=zie(vi×B)，

(3)

其中，Φ是局域电动势，e是电子电荷，ε是介电常数，ci是离子i的局域浓度，ji是离子i形成的局域电流密度，Di是离子i的扩散系数，zi是离子i的电荷数，kB是玻尔兹曼常数，T是热力学温度，Fi是离子i所受的洛伦兹力，vi是离子i的局域流速，B是磁感应强度.

通过有限元方法求解方程的稳态解，方程还需满足连续性方程：

∇·ji=0.

(4)

高斯定理约束了求解边界条件：

(5)

其中，n是法向单位向量，σs是表面电荷密度.当ji在边界处的法向分量为零时意味着没有离子流穿过边界，即

n·ji=0.

(6)

采用有限元方法对具有适当边界条件的耦合偏微分方程进行求解,可以获得分别由阳离子或阴离子贡献的局部离子浓度分布和离子通量,并可以通过对纳米孔横截面上的离子通量密度进行积分来计算通过纳米孔的总扩散电流Ii.

(7)

其中r是纳米孔道的半径.

本研究根据相关文献对MXene二维材料的表征数据[26]建立模型的几何尺寸.其中，单层MXene纳米片的厚度设置为1 nm，片层间距离设置为0.4 nm，同一层的间隙值设置为0.4 nm，二维纳米片上的表面电荷密度设置为-60 mC/m2.

1.7 网格独立性分析

为了提高计算精度和网格质量，对计算区域中的非结构化网格采用自由三角网格的方式来进行网格剖分(图3)，边界层层数设置为3以保证计算精度和计算效率.由于纳米片层的间距较小，离子在其中输运所受的静电场会使其运动情况变得较为复杂，所以需要对近壁面网格进行细化加密处理，如图3的局部放大图所示.为保证计算的独立性，对网格进行无关性分析；分析过程中，以净扩散电流模拟计算值作为判定依据，以网格剖分中的最大单元尺寸为影响因素.

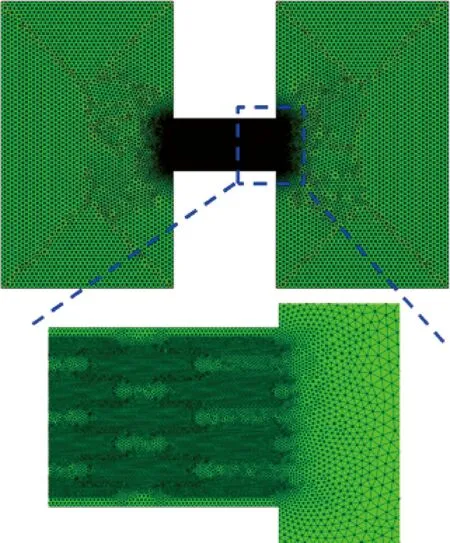
图3 纳米孔道的网格剖分及其局部放大图

如图4所示，从浓度梯度驱动纳米孔道产生净扩散电流的模拟值与网格数目的关系可以看出，净扩散电流的模拟计算值随着网格数目的增加而逐渐减小，当网格数目大于2.8×104时，该值趋于稳定，不随网格数目而波动，具有独立性.简单粗糙的网格会使有限元分析得到的解不精确，而过分细化的网格则会大大增加模型的计算负荷，从而降低运算效率.因此，网格数目为2.8×104时可满足网格无关性分析的要求.

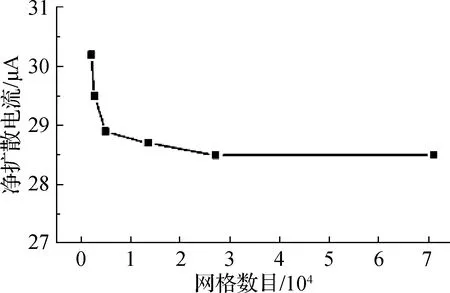
图4 网格数目对纳米孔道产生的净扩散电流模拟计算值的影响

2 结果分析

2.1 膜厚对净扩散电流的影响

在高浓度端的溶液浓度为1 000 mmol/L，低浓度端的溶液浓度为1 mmol/L，MXene膜厚分别为1.03，1.58，2.03，2.34和2.81 μm(经SEM表征)的条件下，通过数字源表测量得到不同膜厚下的净扩散电流，如图5(a)所示分别为1.75，1.57，1.45，1.26和0.90 μA.图5(b)是相同条件下的模拟数据，考虑到模型的收敛性，孔道长度(即膜厚)分别设置为10，30，100，300和1 000 nm.通过多物理场耦合建模以及有限元分析得到不同膜厚下净扩散电流模拟计算值分别为33.23，32.15，29.45，24.27和18.90 μA.实验测量和模拟计算的净扩散电流均随着膜厚的增大而下降.这是因为膜厚表现为体系中的膜阻，所以净扩散电流依赖于欧姆响应，从而随着膜阻的增大而减小.

实验样品的膜厚分布在1～3 μm.模拟时考虑到计算机使用效率以及软件的收敛性等因素，模型中孔道的长度控制在10～1 000 nm.图5中展现模拟计算值和实验测量值采用不同膜厚的对比.这两组数据衔接了两个膜厚区域，衔接点为1 μm的膜厚.从趋势上看，净扩散电流随膜厚的增大曲线斜率增加，两者变化趋势具有一致性.可以发现，衔接点的净扩散电流实验测量值与模拟计算值存在一个数量级的差距.这可能是由于实验中MXene纳米片的间隙大于模拟中设定的间隙值.在实验中，通过真空抽滤法制备的MXene膜，其纳米片间隙大小具有一定的随机性；而在模拟中，考虑到模型的收敛性，纳米片间隙值被设置为0.4 nm.纳米片间隙的增加会削弱双电层效应，因此导致净扩散电流的实验测量值低于相应的模拟计算值.数值模拟能一定程度上体现客观实验的趋势，由于实验条件的限制，接下来针对外加磁场的讨论和分析皆为基于模拟数据的结果，这些结果具有一定的预见性.

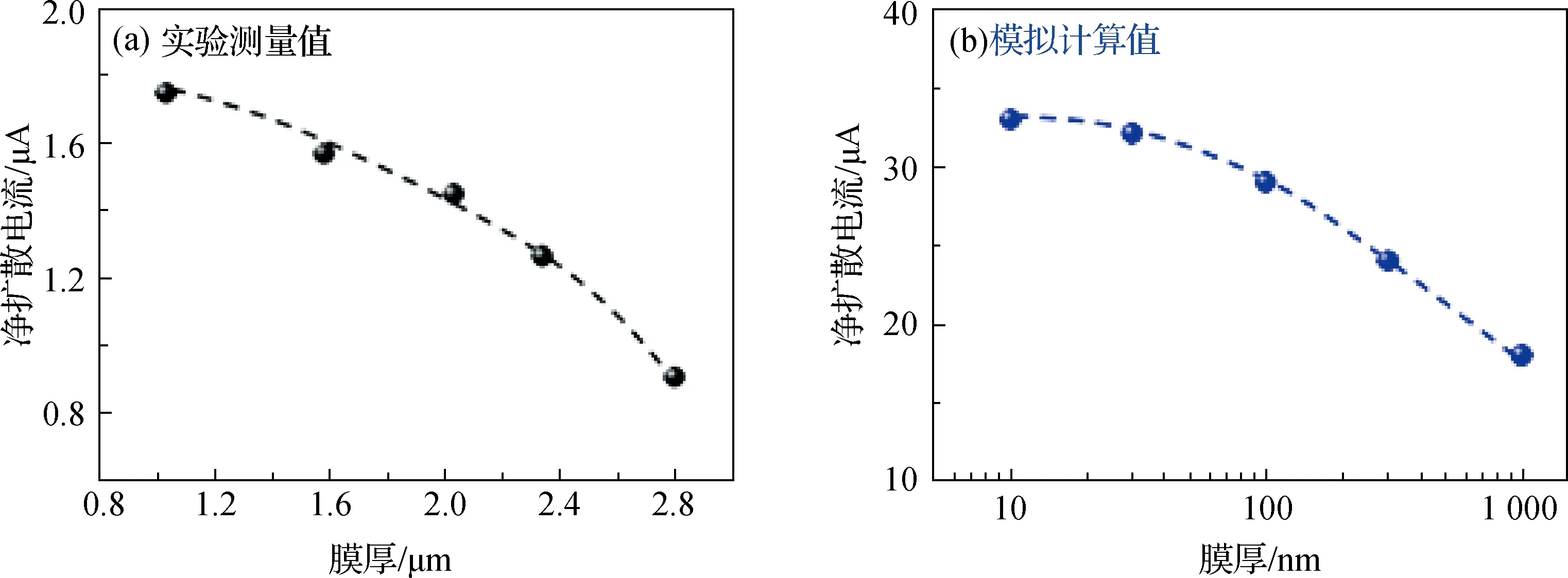
图5 净扩散电流随膜厚的变化

2.2 磁场对净扩散电流的影响

使用COMSOL Multiphysics 5.4版本对模型进行有限元分析计算，其中耦合了交流/直流静电场、稀物质传递场和磁场.计算结果如图6(a)所示，当固定膜厚为100 nm时，可以发现随着外加磁感应强度的增加，纳米孔道中基于浓度梯度驱动产生的净扩散电流也随之增加.这是因为磁场的作用使得偏转离子更多地向纳米片的壁面聚集，等效于增加了纳米片的表面电荷密度，从而增强了双电荷层的效应，所以相应的净扩散电流也得到了提升.当磁感应强度从100 T增至300 T时，净扩散电流的增长速率明显快于磁感应强度大于300 T的情况.这说明当磁感应强度在100～300 T的范围内，净扩散电流会有明显的提升；当磁感应强度大于300 T时，净扩散电流也会提升，但转化效率也会随之下降.此外，净扩散电流会随着浓度梯度的增大而增大.由式(1)和(2)可知，在相同条件下，浓度梯度越大局域电流密度也越大.高浓度端的溶液流向低浓度端的过程中，浓度梯度较大的体系势必有更多的离子参与输运，在双电荷层和磁场的双重作用下会产生更多的净扩散电流.

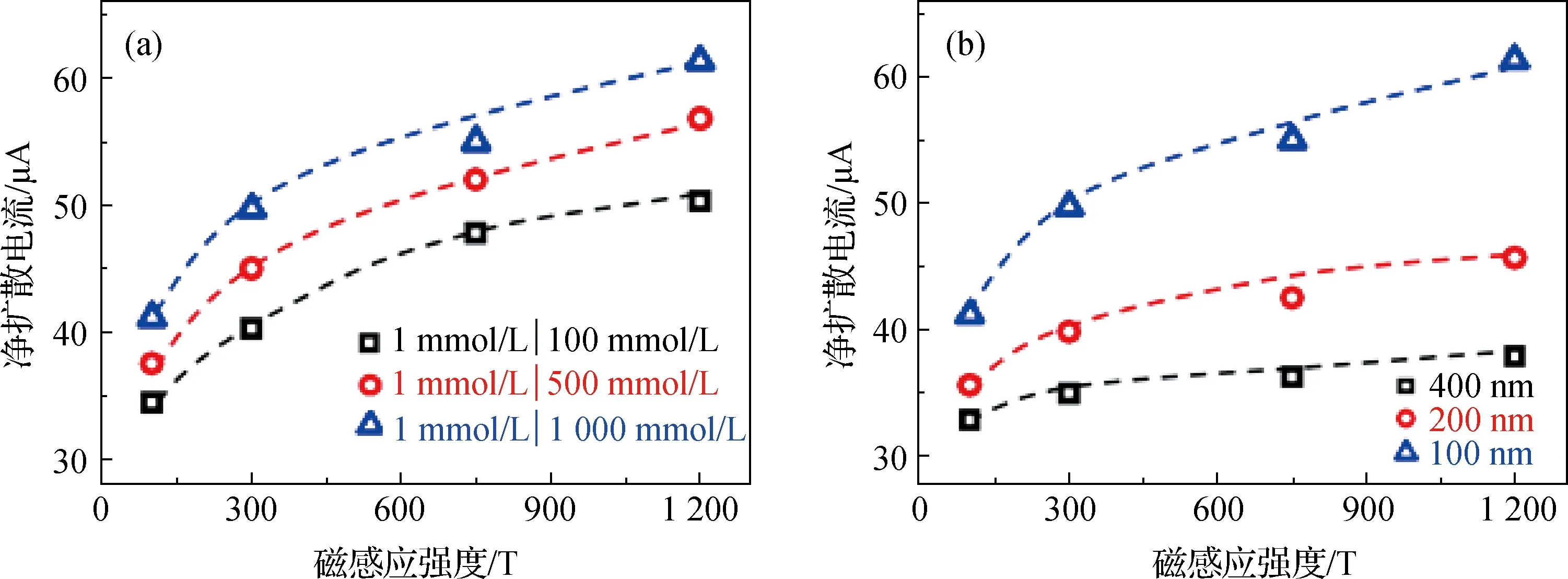
图6 在不同浓度梯度(a)和膜厚(b)下净扩散电流随外加磁感强度的变化

如图6(b)所示，当固定浓度梯度为1 mmol/L|1 000 mmol/L 时，可以发现随着外加磁感应强度的增加，净扩散电流也随之增加.这一点上面已作讨论，这里不再赘述.而随着膜厚的增加，净扩散电流则随之减小.膜厚表现为体系中的膜阻，净扩散电流依赖于欧姆定理，随着膜阻的增大而减小.综上可知磁场对纳米孔道中离子的输运存在影响，离子受到洛伦兹力和双电荷层的耦合作用，从而进一步增大净扩散电流.

2.3 运用磁场进行离子筛分

在COMSOL Multiphysics中将左溶液池设置浓度均为1 000 mmol/L的NaCl和MgCl2的混合溶液，右溶液池设置浓度均为1 mmol/L的NaCl和MgCl2的混合溶液.在浓度梯度的驱动下离子流经纳米孔道，并在双电荷层以及磁场的共同作用下，会发生不同程度偏转，最终在出口处筛分出目标离子.图7(a)为离子筛分模型中Mg2+的浓度分布图.磁场方向与图2一致，即垂直纸面向里，磁感应强度为750 T，纳米孔道表面存在负电荷密度，当高浓度混合溶液通过纳米孔道时，在双电荷层的作用下，纳米孔道内阳离子的扩散会明显优先于阴离子的扩散，因此靠近纳米片壁面处有较高的离子浓度.不仅如此，在磁场作用下，阳离子会受到持续向上偏转的洛伦兹力，从纳米孔道一端迁移至另一端的过程中，更多的阳离子会向出口端上部聚集.由式(3)可知，离子所受洛伦兹力的大小与局域离子流速、离子电荷数以及磁感应强度大小相关.局域流速受到浓度梯度的影响，浓度梯度越大局域流速也越大；反之，则局域流速越小.在该模型中，固定浓度梯度为1 mmol/L|1 000 mmol/L，磁感应强度为750 T，因此离子所受洛伦兹力大小仅与离子电荷数，即离子的价态，呈正相关.

图7(b)为离子筛分模型中Na+的浓度分布图.与Mg2+的浓度分布图相比，在相同的颜色比例尺下，价态更高的Mg2+在出口处被更多地筛分出，浓度显著高于Na+的浓度.分别提取距离出口1 nm附近的浓度数据，得到如图7(c)和(d)所示的结果，Mg2+和Na+的最高稳态分布浓度皆在出口上端0～6 nm范围内.这是由于在洛伦兹力的作用下，阳离子会持续向上偏转，并且Mg2+的价态高于Na+，所以在离子筛分的过程中，Mg2+受到向上偏转的洛伦兹力高于Na+，使得出口上端Mg2+浓度高于Na+浓度，最终达到从混合溶液中筛分出目标离子Mg2+的目的.如图8所示，进一步提取计算模型中出口上端(y=4 nm)与下端(y=-4 nm)的离子浓度并计算相应的离子选择比,得到出口上端筛分Mg2+的离子选择比为1.42，而出口下端筛分Mg2+的离子选择比仅为0.86.通过离子选择比可以标定体系对目标离子的筛分能力，在磁场的调控下，能够有效地筛分不同价态的离子.这可能为未来的核废料处理、盐湖卤水提锂等提供设计思路.

提取(a)和(b)中白色实线的纵向坐标与离子浓度的关系分别得到(c)和(d).

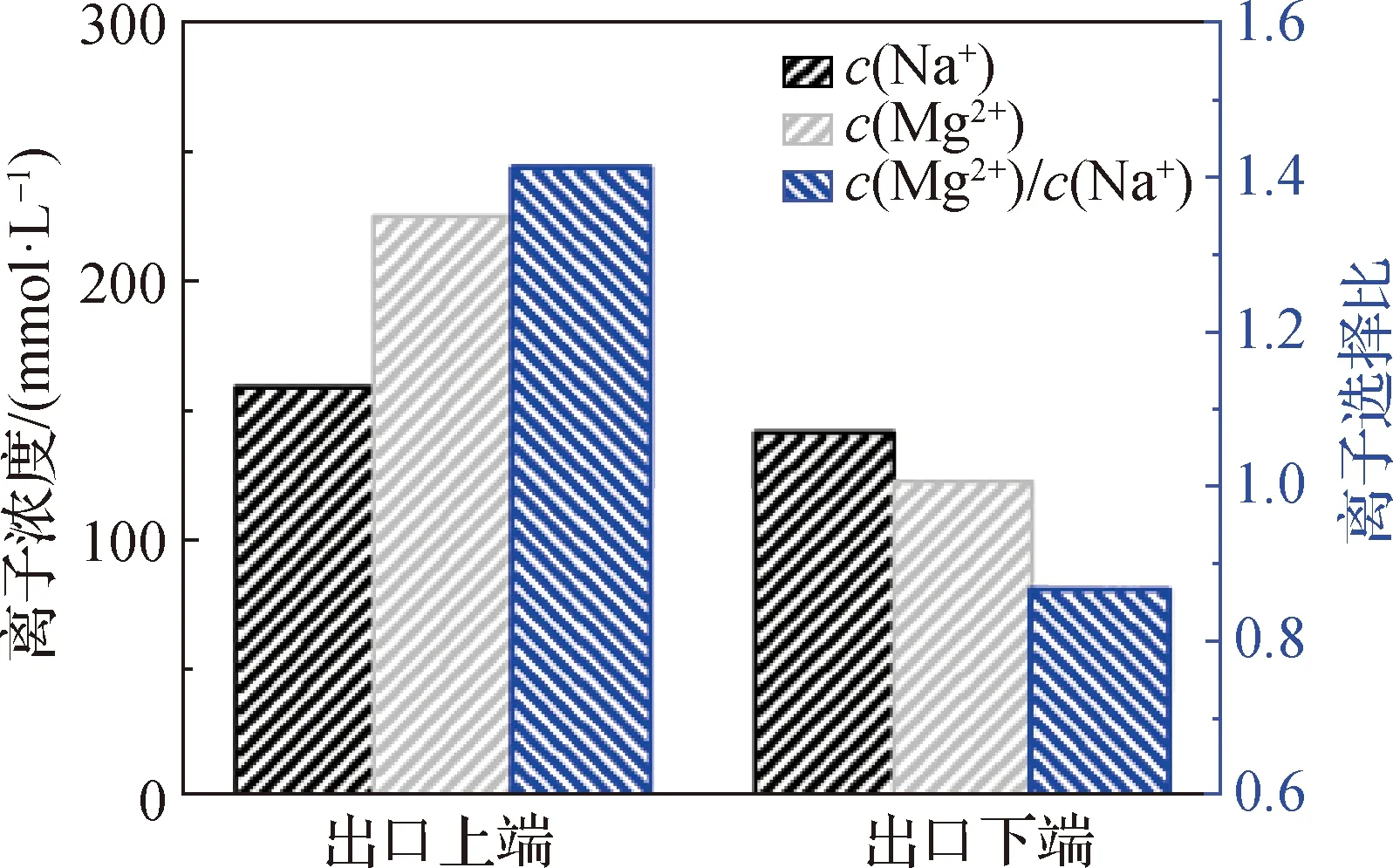
图8 出口上端与下端的离子浓度和相应的离子选择比

3 结 论

本研究通过模拟磁场作用下纳米孔道中离子的输运，分析了磁场对纳米孔道中离子输运的影响并运用磁场对离子进行筛分.首先，通过对比实验测量值与模拟计算值，得到体系的净扩散电流会随着膜厚的增大而下降.然后，进行数值模拟得到，随着外加磁感应强度的增加，纳米孔道中基于浓度梯度驱动产生的净扩散电流也随之增加.这是因为磁场的作用使得偏转离子更多地向纳米片的壁面聚集，等效于增加了纳米片表面电荷密度，从而增强了双电荷层的效应.最后，通过模拟混合溶液中筛分目标离子的模型，提取计算模型出口上端与下端的离子浓度并计算了相应的离子选择比，得到出口上端筛选Mg2+的离子选择比为1.42，而出口下端筛选Mg2+的离子选择比仅为0.86.进一步分析可得，阳离子受到洛伦兹力作用并持续向上偏转，并且由于Mg2+的价态高于Na+，这使得Mg2+受到向上偏转的洛伦兹力大于Na+.离子从孔道穿出后，在出口上端Mg2+浓度高于Na+浓度，从而实现混合溶液中筛分目标离子的应用.