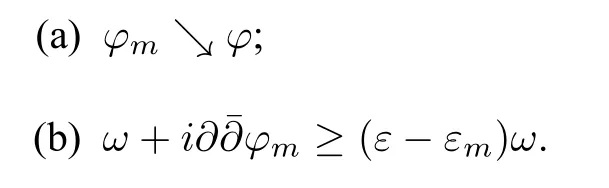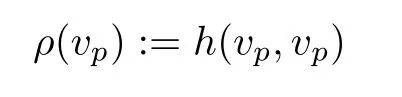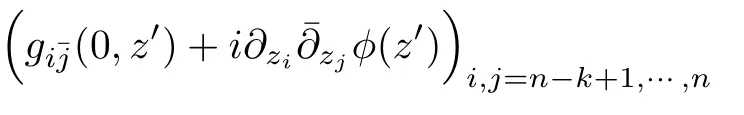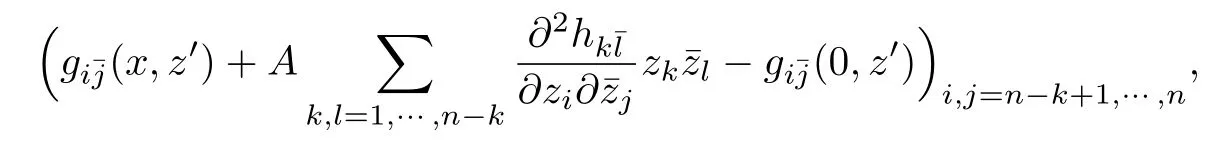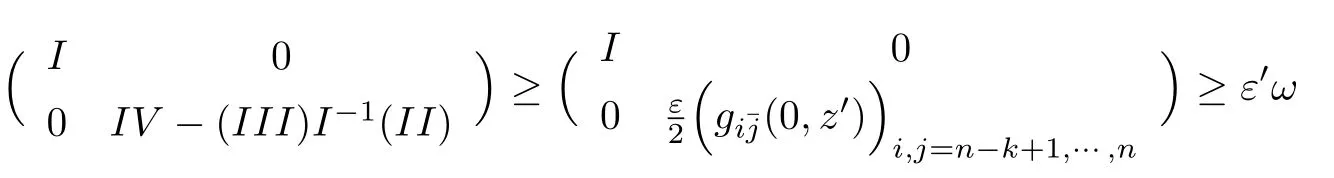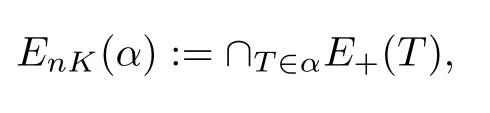Extension of Quasi-plurisubharmonic Functions

Ning Jiafu Wang Zhiwei Zhou Xiangyu

(1.School of Mathematics and Statistics,HNP-LAMA,Central South University,Changsha 410083,China;2.Laboratory of Mathematics and Complex Systems(Ministry of Education),School of Mathematical Sciences,Beijing Normal University,Beijing 100875,China;3.Institute of Mathematics,Academy of Mathematics and Systems Sciences and Hua Loo-Keng Key Laboratory of Mathematics,Chinese Academy of Sciences,Beijing 100190,China;4.School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China)

Abstract In this paper,we give a survey on the extension of (quasi-)plurisubharmonic functions from complex submanifolds.We firstly review the extension of plurisubharmonic functions on Stein manifolds,and then review the extension of quasi-plurisubharmonic functions on compact complex manifolds,including some unpublished new results of the authors Wang and Zhou.

Key words Stein manifold Plurisubharmonic function Kähler manifold Extension

1 Introduction

LetXbe a complex manifold and letφ:X →[−∞,+∞)be an upper semicontinuous function onX.We sayφis a plurisubharmonic(psh for short)function onX,if the restriction ofφto the intersection of any complex line and any coordinate neighborhood is subharmonic.On compact complex manifold there is no nonconstant psh function,but one can work with quasi-plurisubharmonic(quasi-psh for short)function on it.Letθbe a smooth closed real(1,1)-form on a complex manifoldX.Denote byPsh(X,θ)the set ofθ-psh functions onX,i.e.,the set of functionsφ ∈L1(X,R∪{−∞}) which can be locally written as a sum of a smooth function and a psh function,such thatθ+ddcφ≥0 in the sense of currents.Denote bySPsh(X,θ)the set of strictlyθ-psh functions onX,i.e.,the set ofθ-psh functions such thatθ+ddcφ≥ωin the sense of currents for some Hermitian metricωonX.We say thatφhas analytic singularities if for any givenx ∈Xthere exists an open neighborhoodUofxand there exist holomorphic functionsf1,···,fkand a smooth functiongonUsuch that

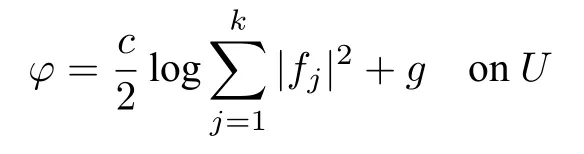
for somec>0.

Plurisubharmonic functions or more generally quasi-plurisubharmonic functions are closely related to holomorphic functions,but they are more flexible.They play important roles in the study of several complex variables and complex geometry,in particular,in the study of the Levi problem and more recently theL2-methods and their applications in complex and algebraic geometry.

In this paper,we survey some recent results on the problem of extending a (quasi-) psh function from a complex submanifold(resp.complex subspace)to the ambient complex manifold(resp.complex space).This is a fundamental problem in the study of(quasi-)psh functions,and has deep relations with the smooth approximation problem of psh and quasi-psh functions,and the extension problems of holomorphic functions or more generally holomorphic sections through theL2-method.The extension problem for quasi-psh functions is summarized as follows.

Question 1.1LetXbe a complex manifold (resp.complex space) andV ⊂Xbe a complex submanifold (resp.complex subspace) of positive dimension.Letωbe a closed real (1,1)-form onX,andφ ∈Psh(V,ω|V).Does there exist a quasi-psh function Φ∈Psh(X,ω),such that Φ|V=φ?

Note that ifω=0,Question 1.1 is a problem of extending psh functions from complex submanifolds.

In section 2,we will present some classical and recent results about the extension of psh functions from complex submanifolds.In section 3,we will present recent progress on the extension of quasi-psh functions on projective and compact Kähler manifolds as well as some applications.

2 Extension of plurisubharmonic functions

In the early study of psh functions,the extension problem was usually connected to the approximation of psh functions by smooth psh functions.On domains in the complex Euclidean space Cn,psh functions can be approximated smoothly on compact subsets by using convolutions with smooth kernels.The global situation for continuous strictly psh function was treated by Richberg [1],by establishing the following technical extension theorem,which was conjectured(and proved in a special case)by Grauert[2].

Theorem 2.1(Richberg,[1]) LetXbe a paracompact complex space,and letY ⊂Xbe a closed complex subspace.Letφbe a continuous(differentiable)strictly plurisubharmonic function onY.Then there exist an open neighborhoodUofYinXand a continuous(differentiable)strictly plurisubharmonic functiononUwith=φ.

However for a psh function which is not assumed to be continuous nor strictly plurisubharmonic,Richberg’s technique is not enough to do such an psh extension,due to the existence of poles and loss of plurisubharmonicity during the gluing procedure.

In 1982,Sadullaev proved the following theorem.

Theorem 2.2(Sadullaev,[3]) IfM ⊂Cnis a closed complex submanifold,then any psh functionuonMpsh-extends to all of Cn,i.e.,there exists a psh functionin Cnsuch that=u.

Thanks to Sadullaev’s theorem,any psh function on a closed submanifold of a Stein manifold can be extended to a psh function on the ambient manifold.The key ingredients in the proof of the above theorem are the following facts:

• any closed complex submanifold of Cn(resp.a Stein manifold) has a holomorphic tubular neighborhood;

• there exists a psh functionϕwith analytic singularities,whose poles are exactly the submanifold.

An important application of Theorem 2.2 is the following approximation theorem.

Theorem 2.3(Sadullaev,[3]) LetMbe a Stein manifold.For anyϕ ∈Psh(M),there is a sequence of smooth plurisubharmonic functions onM,which decreases toϕpointwise onM.

ProofFor the sake of reader’s convenient,we include the proof here.

IfMis Cn,the convolution ofϕwith positive smooth,compact supported,radial functions gives the approximation.For a general Stein manifoldM,there is a proper holomorphic embedding mappingf:M →CN.f(M)is a submanifold of CN,f:M →f(M)is biholomorphic,letg:f(M)→Mbe the inverse off:M →f(M).Then forϕ ∈Psh(M),ψ:=ϕ ◦g ∈Psh(f(M)).By theorem 2.2,there is a Ψ∈Psh(CN),such that Ψ|f(M)=ψ.Thus there is a sequence of smooth plurisubharmonic functions Ψjon CN,which decreases to Ψ pointwise on CN,and Ψj ◦fdecreases toϕpointwise onM.

However,an example given by Fornaess and Wiegerinck[4]shows,for some domainsD,it is not in general possible to approximate psh functions by continuous psh functions on all ofD.

Recently,Coman-Guedj-Zeriahi obtained the following theorem,which says that one can extend psh functions on Stein manifolds with growth control.

Theorem 2.4([5]) LetXbe an analytic subvariety of a Stein manifoldMand letφbe a psh function onX.Assume thatuis a continuous psh exhaustion function onMso thatφ(z)1 there exists a psh functionψ=ψconMsuch thatψ|X=φandψ

The advantage of the above extension with growth control is that it can be applied to extend quasi-psh functions on submanifolds of the projective algebraic manifold,which will be discussed in the next section.

Comparing the assumptions in the above extension theorems,a natural question arises:what one can say about the ambient manifold,if for any subvariety,any psh function on it can be extended to a psh function on the ambient manifold?

We have the following observation.

Proposition 2.1LetMbe a complex space.If for any subvarietyX,and anyψ ∈Psh(X),there exists a Ψ∈Psh(M)such that Ψ|X=ψ,thenMis weakly pseudoconvex.

ProofFor any compact subsetK ⊂M,it is sufficient to prove that

is compact.

3 Extension of quasi-psh functions

As is previously mentioned,Theorem 2.4 can be applied to get the following theorem about the extension of quasi-psh functions on the projective algebraic manifold.

Theorem 3.1(Coman-Guedj-Zeriahi,[5]) LetVbe a subvariety of a projective manifoldXequipped with a Hodge formω.Then anyω|V-psh function onVis the restriction of anω-psh function onX.

By a Hodge form,we mean a Kähler form whose cohomology class is an integral class.The geometric reformulation of the above theorem is as follows.

Theorem 3.2LetVbe a subvariety of a projective manifoldXandLbe an ample line bundle onX.Then any(singular)positive metric ofL|Vis the restriction of a(singular)positive metric ofLonX.

It should be mentioned that under the same assumption as in Theorem 3.2,the conclusion that any smooth positive metric ofL|Vis a restriction of a smooth positive metric ofLonXwas already established by Schumacher in[6].

Theorem 3.1 can be used to prove the following regularization result.

Theorem 3.3(Coman-Guedj-Zeriahi,[5]) LetVbe a subvariety of a projective manifoldVequipped with a Hodge formω.Ifφ ∈Psh(V,ω|V),then there exists a sequence of smooth functionsφj ∈Psh(X,ω)which decrease pointwise onVsuch that limφj=φonV.

This result can be used to show that the singular Kähler-Einstein current constructed in [7] have continuous potentials,for more recent works,see[8].

In the same paper,Coman-Guedj-Zeriahi raised the following extension problem in the compact Kähler setting.

Question 3.4Let(X,ω)be a compact Kähler manifold of complex dimensionn,equipped with a Kähler metricω.LetV ⊂Xbe a complex submanifold of complex dimensionk >0.Is the following

holds?

If the reference function is a smooth strictly quasi-psh function,there is a positive answer to Question 3.4.

Theorem 3.5(Ornea-Verbitsky,[9]; Coman-Guedj-Zeriahi,[5]) LetXbe a compact Kähler manifold equipped with a Kähler formω,and letVbe a complex submanifold ofX.Then

If the reference function has singularities,even in the strictly quasi-psh case,the question is difficult.For strictly quasi-psh function with analytic singularities,Collins-Tosatti established the following theorem by using the resolution of singularities and delicate pinching procedure.

Theorem 3.6(Collins-Tosatti,[10]) Let(X,ω)be a compact Kähler manifold and letV ⊂Xbe a positive-dimensional compact complex submanifold.Ifϕis a strictlyω|V-psh function with analytic singularities onV.Then there is a strictlyω-psh function Φ onXsuch that Φ|V=ϕ.

Similar to the case of Stein manifolds,Wang-Zhou extended strictly quasi-psh functions with arbitrary singularities under the assumption that there exists a holomorphic tubular neighborhood of the submanifold.

Theorem 3.7(Wang-Zhou,[11]) Given a compact Kähler manifold(X,ω)of complex dimensionn,and a compact complex submanifoldV ⊂Xof positive dimensionk

We say thatVhas a holomorphic tubular neighborhood inX,if there is a holomorphic Hermitian vector bundle (E,h)→Vof rankn −k,and there is a biholomorphic mapF:Eδ:={(p,v)∈E:|v|h <δ} →UwithUan open neighborhood ofVinX,for some smallδ >0,such thatF|V:V:={(p,0)∈E} →Xgives the embedding ofVinX.In many cases,Eis taken to be the holomorphic normal bundleNV/XofVinX,e.g.,see[12].

Proof of Theorem 3.7We acknowledge the fact that the proof of Theorem 3.7 here is due to Wang-Zhou,which will not be published elsewhere.

LetT=be the given Kähler current in the Kähler class[ω|V],whereφis a strictlyω|V-psh function.By subtracting a large constant,we may assume that supV φ <−Cfor some positive constantC.

To prove the theorem we need the following lemma.

Lemma 3.1([11,13]) Letφbe a quasi-psh function on a compact Hermitian manifold(X,ω),such thatThen there is a sequence of smooth functionsφmand a decreasing sequenceεm >0 converging to 0,satisfying the following

By Lemma 3.1,we have that there exists a sequence of non-increasing smooth strictlyω|V-psh functionsφmonV,and a decreasing sequence of positive numbersεmsuch that asm →∞

Note that for allm ∈N+,φmsatisfyassumption⋆ε,C.In the following,we will extend all theφmsimultaneously to non-increasing strictlyω-psh functions on the ambient manifoldX.

The proof is divided into three steps.

Step 1:Local uniform extensions ofφmfor allm.Letϕbe a function satisfyingassumption⋆ε,C.SinceVhas a holomorphic tubular neighborhood inX,there exist a holomorphic vector bundleEof rankn −kand an open subsetUofVinX,which is biholomorphic to a neighbourhood of the zero sectionVinE.Letπ:E →Vbe the natural holomorphic projection ofE,andhbe a hermitian metric onE.There is an induced“square distance function”ρdefined onUas

for anyvp ∈Ep.From the holomorphic vector bundle structure,for anyp ∈V,there is a holomorphic local coordinate chart (Up,(z1,···,zn−k,zn−k+1,···,zn)) inUcentered atp,such that (zn−k+1,···,zn)serves as holomorphic coordinates onVnearp,and(z1,···,zn−k)holomorphic coordinates of the fibers ofEwith respect to a holomorphic basise1,···,en−kofEnearp.Writez=(z1,···,zn−k) andz′=(zn−k+1,···,zn),then we haveπ(z,z′)=(0,z′)andρ=∑OnUp,we define

whereAis a positive constant to be determined later.We have the following computations:

In matrix form,we writeas

It is obvious thatII=III∗,whereIII∗is the conjugate transpose ofIII.

One can see thatIis positive definite even ifA=0.Apply a congruent transformation which is independent ofϕ(which depends onI,II,III),to the above matrix,one can get

Now we have to deal with the submatrixIV −(III)I−1(II).

As for the matrix(III)I−1(II),note that

atp,and(III)I−1(II)is totally independent ofϕ,we first choose sufficiently largeA,and then shrinkUp(independent ofϕ)if necessary,such that onUp

Note that

Considering the matrix

as an extension of the matrix of

fromV ∩UtoU,from the assumption,

Since onV,

is positive definite as ak×k-Hermitian matrix,and from the smoothness,we have that up to shrinking(note that the shrinking is independent ofϕ),it is positive definite onU.

For the matrix

from the smoothness ofωandand

atp,up to shrinking(note that the shrinking is independent ofϕ),the following holds onU:

Now onU,we get that

Then we get an open neighborhoodUpnearp,which is independent ofϕ,such that onU,thek×kmatrix

Putting all the computations together,we see that

for some positive constantε′(independent ofϕ).Moreover,we can shrinkUp(the shrinking is independent ofϕ),such that

Lemma 3.2([14]) There exists a functionF:X →[−∞,+∞)which is smooth onX V,with logarithmic singularities alongV,and such thatis a Kähler current onX.By subtracting a large constant,we can make thatF <0 onX.

It is easy to check that Φmsatisfies the following properties:

• Φmis non-increasing inm,

• Φm ≤0 for allm ∈N+,

•

• Φm|V=φmfor allm ∈N+.

Later on,we relax the assumption of the existence of the holomorphic tubular neighborhoods in the above theorem to the existence of the holomorphic retractions.

Theorem 3.8(Ning-Wang-Zhou,[15]) Let(X,ω)be a compact Kähler manifold.LetV ⊂Xbe a complex submanifold of complex dimensionk >0.Suppose that there exist an open neighborhoodUofVinX,and a holomorphic retractionr:U →V.Letφbe a quasi-psh function onVsuch thatfor someϵ>0.Then there exists a quasi-psh function Φ onXsuch that Φ|V=φandonXfor someϵ′ >0.

The main idea is similar to that in[11],with the new ingredient that we need to compute the complex Hessian on a complex submanifold of the square of the Riemannian distance to it.

The following are some examples satisfying the weaker assumption.

Product manifoldLetY1andY2be two compact Kähler manifold and setX:=Y1×Y2.Fix an arbitrary pointp ∈Y2,letV=Y1×{p},then the natural mapπ:Y1×Y2→Y1×{p}gives a holomorphic tubular neighborhood structure ofY1inY2and serves as a holomorphic retraction map.

An interesting example of non-product manifold,communicated to us by Koike[16],is the following famous example of Serre.

Serre’s exampleLetX:=P[x;y]×Cz/∼,whereτ ∈H with H being the upper half plane,and

The submanifoldV:={x=0}ofXis obviously isomorphic to the elliptic curve C/〈1,τ〉.It is easy to check that the projection mapπ:X →C/〈1,τ〉=Vis a holomorphic retraction.It can also be verified thatVdoes not have a holomorphic tubular neighborhood structure inX.

Remark 3.1In[16],Koike gave an interesting proof of Theorem 3.8 for Serre’s example without using the distance function.

Remark 3.2It is worth mentioning that in [17],Wu introduced the concept of nefness in higher codimension to a pseudoeffective(psef for short)class on a compact Hermitian manifold.A psef classα ∈is called nef in codimensionk,if for any irreducible analytic subsetZ ⊂Xof codimension at most equal tok,we have the generic minimal multiplicity ofαalongZas(defined in[18])ν(α,Z)=0.Wu conjectured that a psef class{T}withTa positive current onXis nef in codimensionkif and only if for any irreducible component of codimension at mostkin∪c>0Ec(T){T}|Zis nef in codimensionk −codim(Z,X).Whenk=n,it is a result of Păun[19].It was pointed out by Wu that,a natural idea to attack this conjectural question consists in trying to extend the current on this subvarietyZtoX.If this is possible,the current with minimal singularity would have a potential larger than that of the extended current.In particular,the currrent with minimal singularity would have generic Lelong number 0 alongZ.

Thus it is interesting to study Question 3.4,under the assumption thatωis only assumed to be big or even pseudoeffective.Wang-Zhou have the following partial result.

Theorem 3.9([11]) Let(X,ω)be a compact Kähler manifold of complex dimensionn,andV ⊂Xbe a complex submanifold of positive dimension.Suppose thatVhas a holomorphic tubular neighborhood inX.Letα ∈H1,1(X,R) be a big class andEnK(α)⊂V.Then any Kähler current inα|Vis the restriction of a Kähler current inα.

The non-Kähler locus ofαwas defined in[18]as

whereE+(T)is the set of points ofXsuch that the Kähler currentThas positive Lelong numbers,andTvaries in all the Kähler currents inα.Similarly,in[15],Theorem 3.9 was generalized as the following

Theorem 3.10Let(X,ω)be a compact Kähler manifold of complex dimensionn,andV ⊂Xbe a complex submanifold of positive dimension.Suppose thatVhas a holomorphic retraction structure inX.Letα ∈H1,1(X,R)be a big class and any of the irreducible components ofEnK(α)either does not intersect withV,or is contained inV.Then any Kähler current inα|Vis the restriction of a Kähler current inα.

We note that if the assumption thatωis a Hodge metric in Theorem 3.1 is weaken as the Hodge class{ω}contains a Kähler current,then there are counterexamples for the extension,see cf.[20,Example 4.1].So it is natural to ask if the extension properties put strong restrictions to the reference real (1,1) class associated to the formω.Towards this direction,Matsumura gave a converse to Coman-Guedj-Zeriahi’s result recently.

Theorem 3.11([20]) LetLbe a pseudo-effective line bundle whose first Chern classc1(L)is not zero.Letθ ∈c1(L)be a smooth representative.Assume thatLsatisfies the following property:for any subvarietyVand anyθ|V-psh function,there exists a globalθ-psh functionsuch that=φ.ThenLis an ample line bundle.

It is quite desirable to ask if the extension properties put strong restrictions to the reference real(1,1)class associated to the formωor to the holomorphic structure of submanifolds in the ambient compact Kähler manifold.