5182铝板冲压回弹预测及控制研究*

杨刚 傅涵

台州科技职业学院 浙江 台州 318020

引言

伴随着汽车产业的不断发展，节能减排的要求不断提升，轻量化已成汽车产业发展的一大方向[1]。铝合金具备密度小、抗冲击性能好、比强度大等一系列优点，广泛应用于车身构件中[2-4]。

回弹是车身冲压件成形过程中的三大缺陷之一，它是模具卸载后由于残余应力引起的应变回复现象，且难以避免，它使冲压件的形状及尺寸与冲压模具工作型面的形状和尺寸不符[5]。要使冲压件的形状和尺寸达到设计要求，在模具工作型面设计时必须给出一定的偏离，这个偏离取决于回弹量的大小及分布情况。精确地计算出回弹量的大小及分布情况成为冲压模具设计的关键。

目前，有限元软件已广泛应用于模具设计，但对于回弹还缺乏准确有效的预测，其原因是板料成形是一个复杂的力学过程，它包含几何、物理、边界等强非线性问题[6]。传统有限元模拟所用的本构模型无法真实反映材料在复杂加载路径下硬化特性的变化。在冲压成形过程中，板料会经历反向加载和反复弯曲变形，板料局部产生包申格效应（即材料在某个方向的应变硬化使得反方向的屈服强度降低），材料力学性能发生改变。开模后，冲压件与模具之间的平衡状态被打破，残余应力重新得到平衡，冲压件局部可能产生塑性变形，只有考虑包申格效应才能准确描述局部材料应力应变状态。研究材料的包申格效应不仅可以检验材料本构模型的准确性和可靠性，还为建立准确的本构模型提供依据，将包申格效应应用于材料本构模型，对回弹的研究具有重要意义。

车身铝覆盖件主要集中于5XXX、6XXX系铝板料。目前，5XXX、6XXX系铝板回弹规律的研究较少，考虑包申格效应的5XXX、6XXX系铝板回弹规律的研究更为少见。本研究以5182铝板为研究对象，通过铝板面内扭转试验，研究5182铝板的包申格效应，为构建考虑包申格效应的材料本构模型，从根本上提高5182铝板冲压回弹准确性奠定基础。

2 面内扭转试验

采用1.0 mm厚的5182-O态铝合金冷轧板，其化学成分见表1。

表1 5182铝合金化学成分(wt)%

如图1所示为双桥剪切试样示意图[7]，试验过程中试件内圈固定不动，外圈旋转，带动中间剪切带区域产生塑性变形。相比传统平移式剪切试样，双桥剪切试样可以避免不必要的反作用力或扭矩，并且可以进行循环载荷试验以研究运动硬化现象。

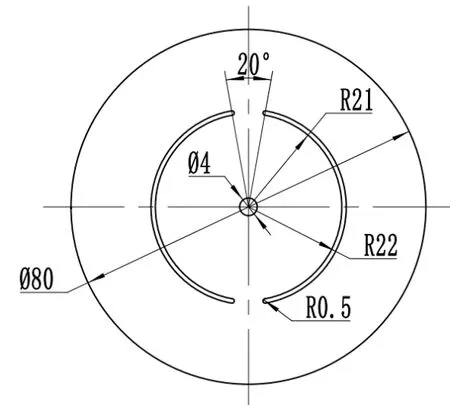
图1 双桥剪切试样示意图

面内扭转试验过程中需要采集到扭矩值-扭转角数据，扭转角可以通过试样的理论角速度相乘时间来计算，但是由于夹具的弹性变形和传动系统的传动间隙，试样的实际角速度和理论速度之间存在差异，尤其是在进行反向加载时。因此，这种计算角度的理论方法并不可靠，无法获得样本的实际扭转角度。

在线测量方法可以测量到试件表面的位移场变化，测量示意图如图2所示，采用理论角速度计算的扭转角表示为θth，基于在线测量方法测量的扭转角表示为θdic，在试样散斑图像中选择两条平行线（线1和线2），线1靠近内部夹紧区域，线2靠近外部夹紧区域，通过计算两条线之间的角度即可得到θdic。

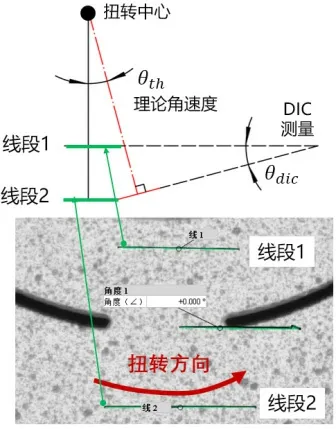
图2 面内扭转试验扭转角测量方法示意图

试样剪切带区域尺寸如图3所示，已知材料所受扭矩M，剪切带长度l0=(α/360).2πrm-2R，剪切带横截面积s=l0.t0，5182铝板各向异性不明显，故假设其为各向同性材料，基于von Mises屈服准则，等效应力σ计算如下：

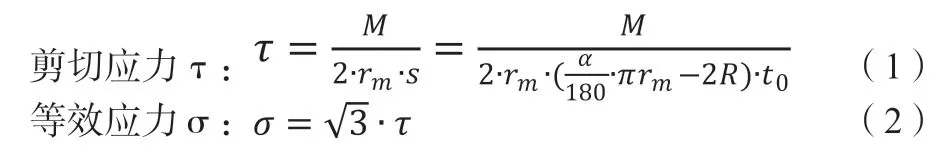
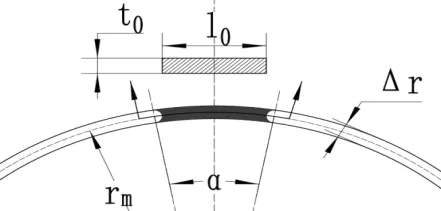
图3 剪切带区域尺寸图

等效塑性应变值ε通过在线测量方法获得，图4分析了1.2°，2.4°，3.6°三种扭转角度下剪切带沿横向截线的等效塑性应变分布，可以看出应变分布并不均匀，应变值集中在边缘区域，中心应变值最小，最大应变和最小应变之间的应变差约为0.6~0.7。

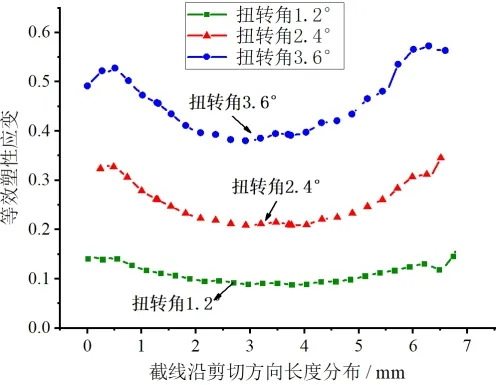
图4 沿剪切带横向应变分布

3 循环加载行为研究

面内扭转试验可以进行正反向扭转，从而实现对板材的循环加载行为研究。图5所示为循环加载试验得到的扭矩值-扭转角曲线。

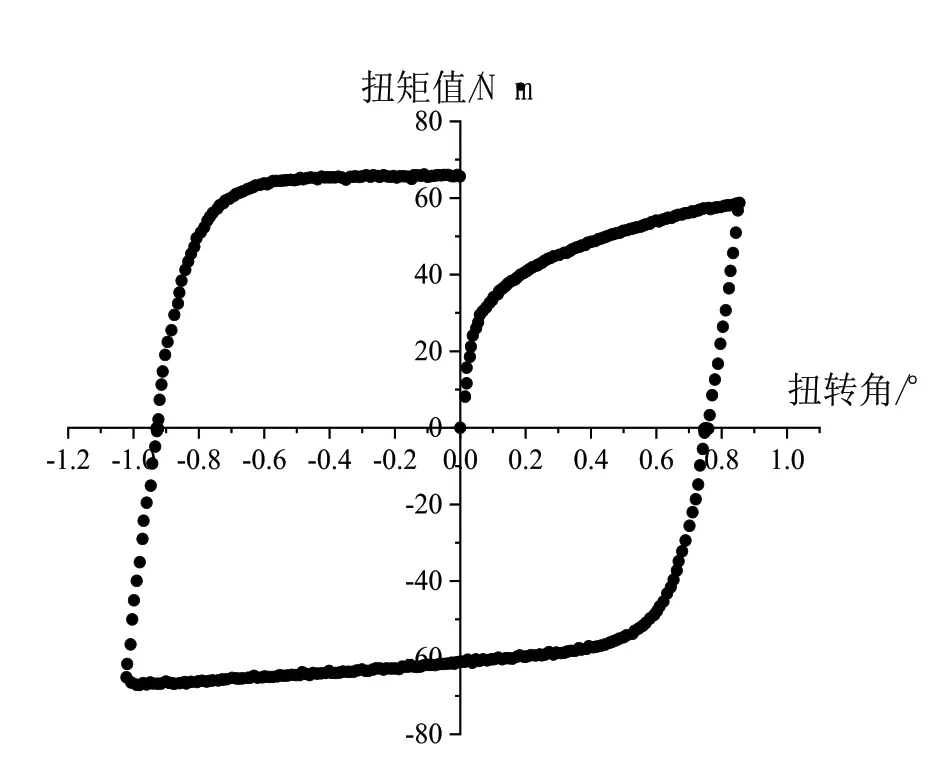
图5 循环加载扭矩值-扭转角曲线

通过正向计算得到图6所示的循环加载应力-应变曲线，可以观察到材料的包申格效应，反向扭转时材料发生再次屈服的屈服强度小于反向扭转前的屈服强度。

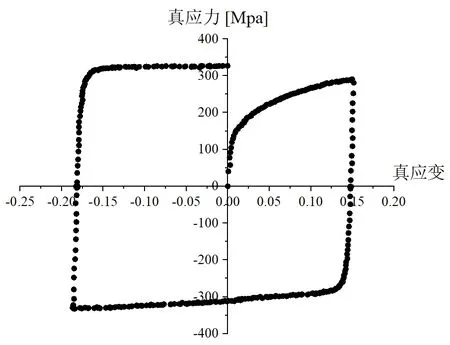
图6 循环加载应力-应变曲线

4 结束语

本文介绍了面内扭转基本原理，针对扭转试验过程中扭转角度的采集，介绍了基于在线测量方法的角度采集方法，对剪切带应变分布不均匀现象进行了分析，通过正向计算方法初步获得了5182材料的应力-应变数据。

进行了循环加载试验，得到了扭矩值-扭转角曲线，并通过正向计算得到了循环加载应力-应变曲线，观察到了铝板的包申格效应。