构造奇数平方阶最完美幻方的方法

詹 森，王辉丰

（1.广东技术师范大学 计算机科学系，广东 广州 510665；2.海南师范大学 数学与统计学院，海南 海口 571158）

文献[1]解决了构造双偶数阶最完美幻方的棘手难题，给出了理论证明。文献[2]将其推广到双偶数阶空间最完美幻立方。在此基础上，本文进而给出构造n2(n= 2m+ 1，m是自然数)阶最完美幻方的三步法及其证明，我们还可给出构造奇数平方阶空间最完美幻立方的方法(见注)，这就比较全面解决了构造最完美幻方及幻立方的难题。

分三部分讨论奇数平方阶最完美幻方的构造方法如下：

1 奇数平方阶最完美幻方的定义[1-3]

类比双偶数阶最完美幻方的定义[1]，给出奇数平方阶最完美幻方的定义如下：

设任一个n2(n= 2m+ 1，m是自然数)阶幻方为Ω，若Ω是一个中心对称完美幻方且满足：1）从Ω中任一点出发，在同一行中向右依次取相距k个位置（k=1，2，…，n）的数直至取到第n个数，再以这些数为起点在同一列中向下依次取相距k个位置（k=1，2，…，n）的数直至取到第n个数，由这些数组成一个n×n方阵（包括跨边界的n×n方阵），其n2个数字的和都等于n2阶幻方的幻方常数；2）从Ω中任何一个位置出发，按国际象棋中的马步沿一个方向走下去，历经n2步必回到出发点，所历经的n2个数字之和都等于n2阶幻方的幻方常数，则Ω称为n2(n= 2m+ 1，m是自然数）阶最完美幻方（见定理及证明）。

显然，除奇数平方阶最完美幻方外，不存在任何其他奇数阶幻方是最完美幻方。

2 构造n2(n = 2m + 1，m是自然数)阶最完美幻方的三步法

第1步 构造n2阶基方阵A

给定一个n阶中心对称幻方A*，从第一行开始由上至下逐行排列成一个1×n2的矩阵，称为基本行。以基本行作为基方阵A的第m+ 1行，第m+ 1行左（或右）移n个位置得第m行，第m行左（或右）移n个位置得第m- 1行，依次类推直至得到第一行。第m+ 1行右（或左）移n个位置得第m+ 2行，第m+ 2行右（或左）移n个位置得第m+ 3行，依次类推直至得到第n行，得一个n×n2矩阵，记为A**，n个矩阵A**从上到下排列在一起所得就是n2阶基方阵A。

显然，第1+t⋅n行（t=0，1，…，n-1）相同，第2 +t⋅n行（t=0，1，…，n-1）相同，…，第n+t⋅n行（t=0，1，…，n-1）相同。

n2阶基方阵A位于第h*=h+s⋅n行，第k*=k+t⋅n列的元素为a(h*,k*)，其中h，k=1，2，…，n；s，t=0，1，…，n-1。

第2步 求基方阵A的转置方阵B

把基方阵A的列作为方阵B的行，把基方阵A的行作为方阵B的列，所得方阵B就是基方阵A的转置方阵。

第3步 基方阵A中的元素减1后乘以n2再加上转置方阵B的对应元素，所得n2阶方阵记为Ω，就是n2阶最完美幻方。不同的n（n=2m+1，m是自然数）阶中心对称幻方可得不同的n2阶最完美幻方。

3 定理及证明

定理 方阵Ω就是一个n2阶最完美幻方。

证明 第1步 证明基方阵A是一个非正规的n2阶最完美幻方。

2）因为基本行是中心对称的，由基本行得n×n2矩阵A**过程也是中心对称的，所以矩阵A**是中心对称的，从而n2阶基方阵A是中心对称的。

3）计算基方阵A从左上角到右下角的对角线和泛对角线上所有元素的和。由文献[4]的余函数法，设R(x)是周期为n2的余函数，r(x)是周期为n的余函数。

由a(f*+ 1,1)开始的从左上角到右下角的对角线和泛对角线上元素a(h*,k*)的共性是R(h*-k*)=f*，其中，h*，k*=1，2，…，n2，f*=0，1，…，n2-1，不同的f*对应不同的对角线或泛对角线，在求和的过程中f*是固定的。为简单起见，R(h*-k*)=f*简记为μ*，出于同样的考虑，r(h-k) =f简记为μ，其中，h，k=1，2，…，n，f=0，1，…，n-1，计算基方阵A从左上角到右下角的对角线和泛对角线上所有元素的和为

由a(f**,n2)开始的从右上角到左下角的对角线和泛对角线上元素a(h*,k*)的共性是R(h*+k*)=f**，其中，h*，k*=1，2，…，n2，f**=0，1，…，n2，不同的f**对应不同的对角线或泛对角线，在求和的过程中f**是固定的。为简单起见，R(h*+k*)=f**简记为ν*，出于同样的考虑，r(h+k)=fˉ简记为ν，h，k=1，2，…，n，f=0，1，…，n，计算基方阵A从右上角到左下角的对角线和泛对角线上所有元素的和为

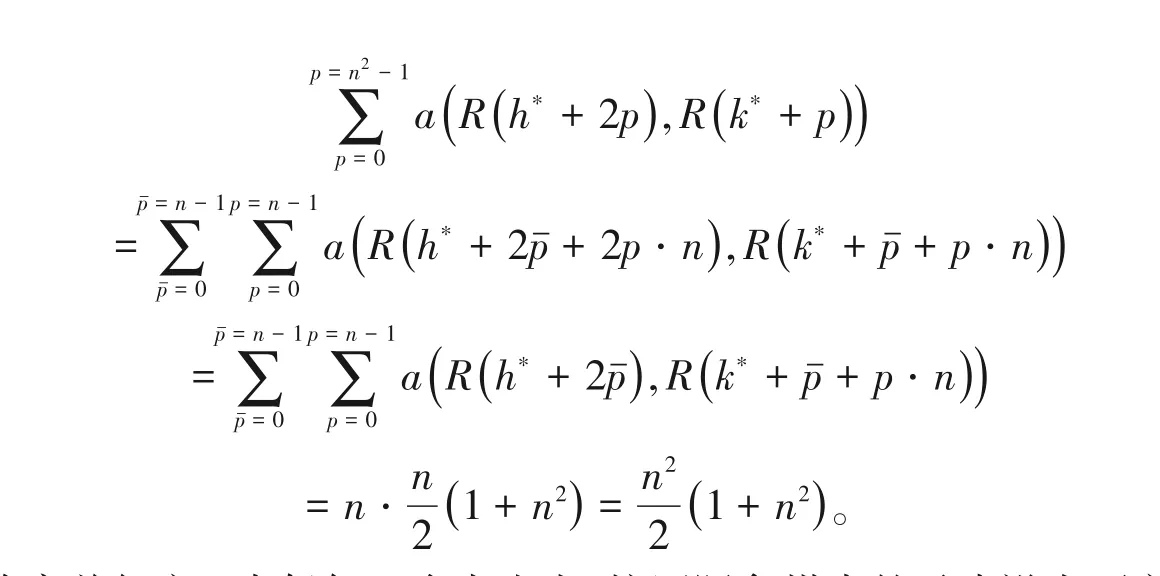
因而从非正规对称完美幻方A中任何一个点出发，按国际象棋中的马步沿右下方向直着走下去，历经n2步必回到出发点，所历经的n2个数字之和都等于非正规对称完美幻方A的幻方常数。当沿右下方向横着走下去，结果相同：

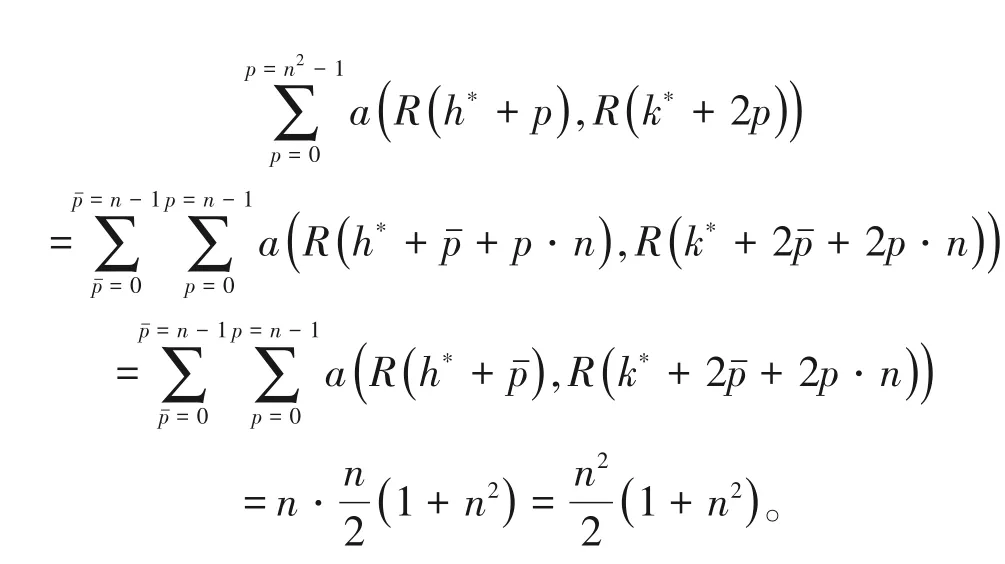
同理，顺着其他方向走马步结果都相同。

综上所述，基方阵A是一个非正规的n2阶最完美幻方。

第2步 显然，基方阵A中的元素减1后乘以n2所得方阵是一个非正规的n2阶最完美幻方，转置方阵B也是一个非正规的n2阶最完美幻方。基方阵A中的元素减1后乘以n2再加上转置方阵B的对应元素，所得n2阶方阵Ω就是一个非正规的n2阶最完美幻方。

第3步 以基方阵A笫一行的元素表示其其他元素

其中，k*= 1,2,…,n2,p= 0,1,…,n2- 1。

设转置方阵B位于第h*行第k*列的元素为b(h*,k*)，其中h*,k*= 1,2,…,n2，a(1+p,R(k*+p⋅n))所对应的元素为

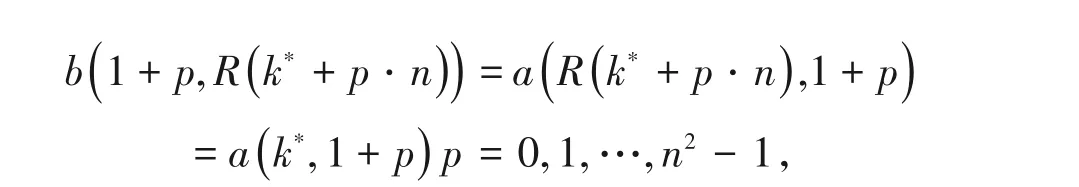
为基方阵A位于第k*行的元素，即1，2，…，n2的自然数。

基方阵A中的元素减1后乘以n2所得方阵由形如p⋅n2（p= 0,1,…,n2- 1）的数所组成。基方阵A中的元素减1后乘以n2再加上转置方阵B的对应元素，所得n2阶方阵Ω由形如p⋅n2+h*（p= 0,1,…,n2- 1,h*=1,2,…,n2）的数所组成，即由1，2，…，n4的自然数所组成。综上所述，方阵Ω是一个正规的n2阶最完美幻方。

由第一步n×n2矩阵A**的安装知，每一个n阶中心对称幻方按本文的三步法可产生两个不同的正规的n2阶最完美幻方。根据在文献[4]给出的构造奇数阶对称幻方或奇数阶对称完美幻方的二步法，共可产生2m+1(m!)种不同的n(n= 2m+ 1，m是自然数)阶对称幻方或对称完美幻方，相应地就可产生2m+2(m!)种不同的正规的n2阶最完美幻方。由于存在其他构造奇数阶对称幻方的方法，所以实际上可得到比2m+1(m!)更多的正规的n2阶最完美幻方。

例 由5阶对称幻方产生的25阶最完美幻方（见图1、2）。

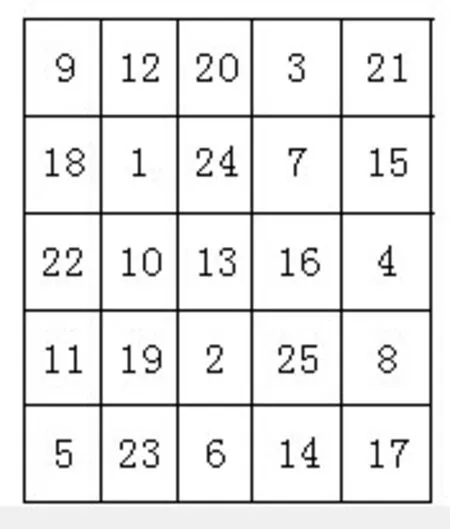
图1 5阶对称幻方Figure 1 5 order symmetric magic square

图2 25阶最完美幻方Figure 2 25 order most perfect magic square