有关科氏加速度的疑难问题探究

郑 金

(凌源市职教中心 辽宁 朝阳 122500)

科里奥利加速度和科里奥利力是理论力学教学中的重点和难点，有关科氏加速度和科氏力的疑难问题较多，本文将选择其难度较大而且比较有趣的3个方面进行答疑解惑，通过具体问题进行分析说明.

1 推导科氏加速度公式的矢量式

在图1中，动点沿直杆AB运动，而杆又绕A轴匀速运动.设直杆匀速转动的角速度为ω，动系固结在杆AB上.在瞬时t，动点在M处，它的相对速度和牵连速度分别为vr和ve.经过时间间隔Δt后，杆转到位置AB′，动点移动到M3，这时它的相对速度为v′r，牵连速度为v′e.设动点的相对加速度和牵连加速度分别为ar和ae.试证明下面两个等式[1]：

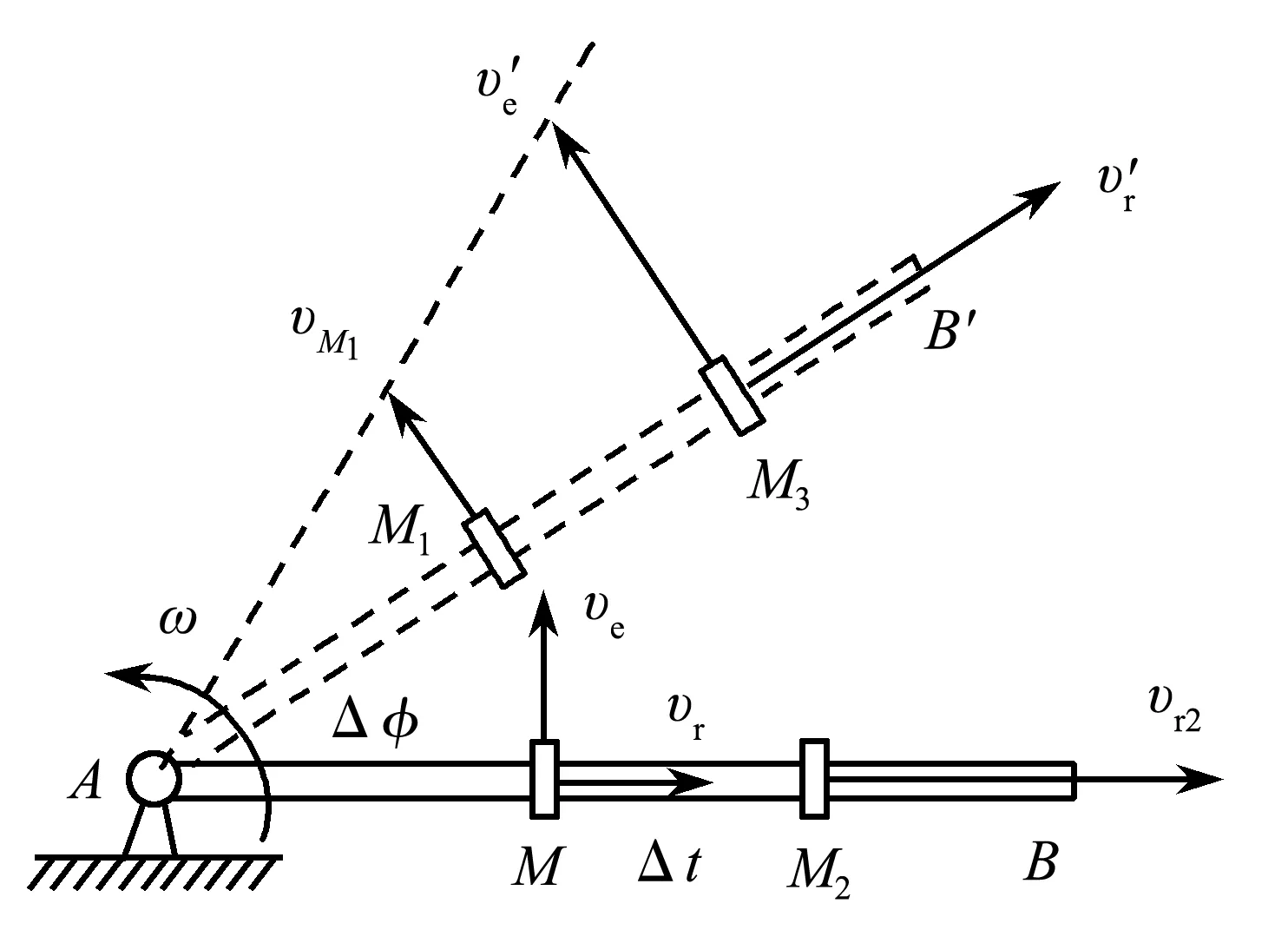
图1 动系做圆周运动

可利用加速度定义、极限知识以及矢量的叉积知识来证明.

首先证明第一个等式.由图1可知，若不考虑相对速度方向变化，则质点沿杆方向的相对加速度为

在图2中，相对速度大小满足vr2=v′r，将相对速度矢量vr2与v′r进行平移，始端重合于O点，如图2所示，可知相对速度矢量三角形为等腰三角形，其中底边的长度Δvr表示相对速度变化量的大小.

图2 相对速度矢量三角形

在很短时间内，等腰三角形可视为由匀速圆周运动形成的扇形，底边长度近似等于圆弧长度，而当Δt→0时，有vr2→vr，可知因方向变化而产生的相对速度变化量的大小为Δvr≈vr2Δφ≈vrωΔt.

由此可得相对速度变化率的大小为

在很短时间内，圆心角Δφ很小，由图2可知相对速度变化量的方向几乎垂直于相对速度的方向，即垂直于约束轨道.由于矢量ω与vr垂直，利用右手螺旋定则可知叉积ω×vr的方向也垂直于约束轨道，即与相对速度变化量的方向一致，由此可知，因相对速度方向变化而产生的加速度的矢量式为

由图1可知，相对速度矢量的总变化率为

考虑到数学公式[2]

lim[f(x)+g(x)]=limf(x)+limg(x)

可得

即

这表明，相对速度矢量的变化率等于相对加速度与科氏加速度一半的矢量和.

下面证明第二个等式.牵连速度矢量的总变化率为

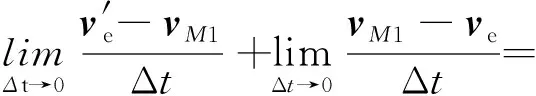
所以

这表明，牵连速度矢量的变化率等于牵连加速度与科氏加速度一半的矢量和.

由于绝对速度等于相对速度与牵连速度的矢量和，即v=vr+ve，可知

即

a=ar+ae+2ω×vr

这表明，绝对加速度等于相对加速度、牵连加速度与科氏加速度的矢量和[3].

所以科氏加速度公式的矢量式为aC=2ω×vr.

相对运动(质点沿杆运动)改变了牵连速度ωr的大小，产生了横向加速度ωvr；同时，牵连运动(直杆转动)改变了相对速度vr的方向，由此产生横向加速度ωvr，二者之和为科氏加速度2ωvr.

2 在无刚性约束情况下的科氏加速度公式

如图3所示，有一水平圆盘以角速度ω匀速转动，圆盘表面光滑，一质点在沿半径方向相对于地面以速度v做匀速离心运动，若开始位置到圆心的距离为r0，求质点相对于圆盘运动的科氏加速度随时间变化的关系式.

图3 质点在水平转盘上运动

在地面参考系中，质点做匀速直线运动.在圆盘参考系中，质点做曲线运动，由此可知，在非惯性系中，质点产生了加速度，而且受到惯性力的作用.

对于沿顺时针方向转动的圆盘，若假设圆盘静止不动，则质点相对于圆盘向逆时针方向偏转，如图4所示.质点在沿半径方向做匀速直线运动，速度为v∥=v，在垂直于半径方向的速度为v⊥=ω(r0+vt)，相对于圆盘的合速度为

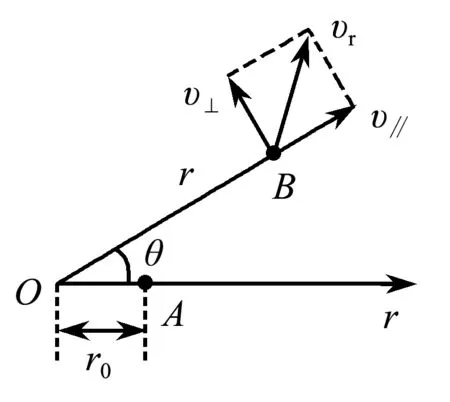
图4 质点相对于转盘偏转

可知在垂直于相对速度方向的科氏加速度为

值得注意的是，在垂直于半径方向的科氏加速度aC⊥=2ωv∥=2ωv只是一个分量，但在一般情况下所说的科氏力和科氏加速度，都是针对相对运动的合速度而言.在无约束的情况下，在非惯性系中的科氏加速度与科氏力的方向相同，由图3和图4已知圆盘转动的角速度、相对速度以及科氏加速度三者的方向，为了遵循右手螺旋定则，科氏加速度公式的矢量式需带负号，即为aC=-2ω×vr.其中的负号只用来表示方向相反.

在实际问题中，匀速转动物体不一定是直杆或圆盘，相对运动质点的初速度不一定沿半径方向，相对运动速度不一定保持不变，但科氏加速度公式和科氏力公式普遍适用.

3 利用科氏加速度公式解答实际问题

【例题】[3]如图5所示，一个用金属丝做成的半径为R的光滑圆圈，绕竖直直径按逆时针方向(俯视)以角速度ω匀速转动，圆圈上套着一个质量为m的小环，刚开始小环从圆圈的最高点无初速下滑，试求当小环与圆心的连线跟竖直方向的直径夹角为θ时，小环的科氏加速度的大小和方向.

图5 例题情境图

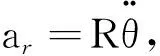
对各项取积分可得

所以小环在地面参考系中的科氏加速度的大小为

应用右手螺旋定则可知科氏加速度的方向垂直于圈面向里.

还有一种非常简单的解法:以圆圈为参考系，利用离心势能公式[4]，由机械能守恒定律列方程

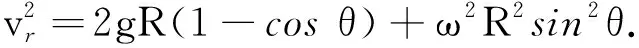
解题关键是求解相对速度，由于小环在圆圈的切线方向不受圆圈的弹力，因此可在切线方向应用牛顿第二定律列方程；由于小环在水平方向受到圆圈的侧向弹力对其做功，因此不能在惯性系中应用机械能守恒定律列方程.而科氏加速度正是由侧向弹力产生，这个弹力属于非保守力，即是水平方向的约束反力，因此与科氏力大小相等，方向相反.求出科氏加速度的意义在于可用来求侧向弹力.

总之，在圆周运动与相对运动相互影响的情况下，质点做曲线运动，由此产生科氏加速度.在惯性系中产生科氏加速度的力是约束反力，在非惯性系中产生科氏加速度的力是科氏力.科氏力只存在于非惯性系中，并且与洛伦兹力有相似之处.在对叉积中的角速度与相对速度确定先后次序的条件下，对于有无约束的两种情况，科氏加速度共有两个公式，即分别带正负号，而科氏力只有一个公式，带负号.