基于模糊多准则决策模型的废弃矿井抽水蓄能电站选址研究

2021-11-06王兵刘朋帅邓凯磊

矿业科学学报 2021年6期

王兵刘朋帅邓凯磊

中国矿业大学(北京)能源与矿业学院,北京 100083

根据我国《煤炭工业发展“十三五”规划》的煤炭生产结构优化指标,2015年我国的矿井数量为9 700 处,到2020年,煤矿数量控制在6 000 处左右,矿井数量减少了3 700 处。随着去产能的深入推进,废弃矿井数量将会越来越多,到2030年废弃矿井数量将达到1.5 万处,废弃地下空间将达到25.8 Gm3[1-2],且废弃矿井中矿井水资源、地热资源丰富[3]。针对废弃矿井的二次利用方式,中国工程院提出了建设分布式抽水蓄能电站、开发利用资源枯竭露天矿空间资源、开发可再生能源等方面的政策建议[1]。因此,废弃煤矿资源化利用是煤炭工业矿后管理的重要方向,探索废弃煤矿资源化的创新性和战略性解决方案具有十分重要的意义。

在全球低碳经济背景下,为了实现可持续发展,可再生能源应用已成为节能减排的重要途径。截至2019年,全球可再生能源发电装机容量达2 536.8 GW,其中我国占比为29.9% ,居全球首位。然而,风能和太阳能利用存在固有的波动性和间歇性[4-5],弃风弃光限电问题突出。而抽水蓄能电站以其独特的调峰填谷、启停迅速等优点,逐渐获得能源电力公司的重视。

抽水蓄能电站在我国未来可再生能源结构中会占很大的比重,此类电站既是发电厂,又是用户,其不仅运行灵活而且还可实现高达80% 的整体效率[6]。 2014—2018年我国抽水蓄能市场规模不断扩大。根据中关村储能产业技术联盟(CNESA)全球储能项目库的不完全统计,截至2018年底,中国已投运储能项目累计装机规模31.3 GW,其中抽水蓄能的累计装机规模最大,为29.99 GW,同比增长4.86% ,占全国储能装机总规模的96%[7]。根据国家能源局发布的《水电发展“十三五”规划》,到2020年底,我国抽水蓄能的累计装机规模达到40 GW,2025年将达到90 GW。

废弃矿井建设抽水蓄能电站拥有成本低、资源便捷、容易改造等优势。近1/3 的废弃矿井为水资源丰富矿井[8]。水力发电需要的高落差与废弃矿井本身具有的深度差高度匹配。利用废弃煤矿采空区建设抽水蓄能调峰系统,能够克服传统抽水蓄能电站的选址局限,减少建设成本与建设周期,为我国废弃煤矿的转型发展和地下空间资源的利用提供新的方向和思路。

本文主要针对抽水蓄能电站在废弃矿井中的选址问题开展研究。将常规抽水蓄能电站选择的决定因素与废弃矿井独特的地形条件相结合,确定抽水蓄能电站在废弃矿井中建站选址的指标体系,从而为废弃矿井抽水蓄能电站选址提供了一个新思路。首先,基于指标体系,采用初步筛选和决策遴选开展选址决策;其次,专家对选址因素打分,确定废弃矿井为抽水蓄能电站选址的决定性指标;然后,运用三角模糊数权重计算方法计算其权重[9];最后,运用模糊多属性群决策排序方法对备选废弃矿井进行优化排序,给出最适合作为抽水蓄能电站的废弃矿井的决策建议。本文基于对不确定环境下多属性群决策方法的研究,将多属性群决策模型应用于废弃矿井-抽水蓄能电站选址问题,为抽水蓄能电站选址提供了新的研究方案。

1 研究现状及发展趋势

1.1 废弃矿井抽水蓄能电站选址的决策指标及方法

抽水蓄能电站站址的选择直接影响抽水蓄能电站的规模、布局、收益和投资。 Nzotcha 等[10]在可持续视角下提出了包括技术经济、社会、环境等影响站址选择的因素。抽水蓄能电站还可与其他可再生能源相结合,风—光—抽水蓄能联合发电系统优化调度研究[11]。梁海波[12]提出站址的选择应当具备较大的水位差、必要的水源、良好的地形条件和地理位置等。庞伟等[13]从经济角度考虑抽水蓄能电站选址决策中对电网削峰填谷的重要性,认为经济性始终是电站的首要因素。废弃矿井的抽水蓄能电站建设不仅需要考虑常规抽水蓄能电站的选址因素,还需要结合废弃矿井特有的一些因素。抽水蓄能电站的建设选址为多属性决策问题,不仅需要考虑自然、社会、经济,还要考虑地下空间及库容、地下围岩支护稳定性等因素[14-15]。现有研究在解决多属性决策问题时,侧重于以单个决策者为研究主题,即使在面对群体决策问题时,也多是将群体割裂成个体,把群决策问题转化为若干单一主体的问题,然后利用现有方法分别对单一主体的决策问题进行处理。

主观赋权法是研究较早且较为成熟的方法,需要专家根据经验确定属性的重要程度,许多学者采用主观赋权法研究选址问题。娜仁花[16]利用层次分析法(AHP)构建选址的评价模型,根据备选地点各指标进行判断。若只用该方法,则受主观因素的影响大。在多准则决策中,决策指标以及决策目标数量很多时,模糊AHP 的计算会很复杂,并且可能会出现超模糊现象,造成评判失败[17]。 Tan等[18]在研究选址问题时采用熵权法计算客观权重,但在样本数据较少时可能会发生不准确计算,确定的权重会与实际重要程度相悖。

许多学者采用模糊TOPSIS 方法进行方案决策。任嵘嵘等[19]通过计算每个备选方案与理想方案的模糊距离,判断亲密系数,并最终应用于最佳方案的抉择。尹胜等[20]充分考虑区间直觉模糊决策的直觉性和模糊性因素,运用改进的模糊熵公式计算决策属性指标的权重值,提高决策指标权重的客观性。张丽媛等[21]针对三角模糊偏好下冲突型群决策问题,提出通过计算各个方案群偏好矢量与理想方案偏好矢量之间的加权相似度,来选出最优方案。模糊多准则决策方法在选择最优方案问题中得到了广泛应用。

本文对多属性群决策问题中的属性权重计算和方案排序方法进行整理和探讨,运用模糊多准则方法、TOPSIS 决策方法,结合不确定性理论提出了一种方案排序方法,用于解决实际决策中的不确定性问题。表1 列出了废弃矿井与抽水蓄能结合可用的决策指标及方法。本研究主要针对指标权重计算,建立综合评判模型,运用TOPSIS 法计算评价对象与理想点之间的贴近度,取得了很好的效果。

表1 废弃矿井抽水蓄能选址的决策指标及模型方法Tab.1 Decision index and method for site selection of pumped storage power station in abandoned mines

1.2 废弃矿井抽水蓄能选址的决策体系

废弃矿井各类资源必须在安全和经济的前提下开发利用,需要综合考虑影响选址的各种因素。研究确定用于选址问题的一级指标5 个,二级指标22 个。一级指标因素包括自然因素、社会因素、环境因素、经济因素、安全因素5 个方面。自然因素包括水位差[16]、地下空间[35]、地形条件[35]、巷道长度[26]和矿井水量[36];社会因素包括与城市距离[37]、土地利用程度[37]、当地用电需求量[38]和就业率[37];环境因素包括当地有效风速[39]、平均降水量[40]、太阳辐射时间和与公共设施距离[41];经济因素包括与公路线距离[12]、当地最高电价[42]、与电网距离和场地改造难易程度[40];安全因素包括地质灾害发生频率[43]、地质稳定性[44]、岩土透水性、地震类别和地下围岩支护稳定性[44]。这22 个指标因素对于抽水蓄能应用于废弃矿井中起着关键性的作用。决策指标树状图如图1 所示。

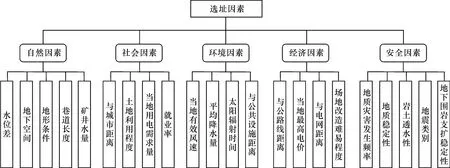
图1 抽水蓄能废弃矿井选址决策因素Fig.1 Decision factors for site selection of pumped storage power station in abandoned mines

2 研究方法与模型

2.1 基于专家打分的指标权重计算方法

本文选取专家打分法,邀请抽水蓄能和矿业工程领域经验丰富的专家对各指标打分,并计算其权重。具体步骤如下:

(1) 确定专家。聘请相关领域研究人员作为评分专家,为了使权重确定更加准确,通常人数不低于5 人。本研究邀请5 位来自矿业经济、矿业工程管理和矿业技术三个领域的专家,对本研究的指标因素进行重要性评判,基于因素重要程度进行打分。

(2) 确定项目的重要性。针对不同的决策指标,每位专家采取两两比较法,对项目的重要性进行比较。本文问卷发放5 份,全部收回。

(3) 选取1-9 标度打分法[45]。选择多名专家构成群体对属性重要程度进行评判,构成一个打分矩阵。假设多属性决策问题有n个指标因素,s个专家,可应用两两比较方法,s位专家对评价属性的相对重要性进行打分,第k个专家的打分矩阵表示为

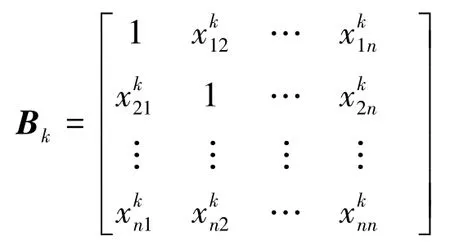
将专家打分得来的判断矩阵运用AHP 进行整合,并得出指标因素的权重及方案评价。检验判断矩阵的一致性,求出矩阵的最大特征值和相应的特征向量,并对最大特征向量进行归一化处理,得到指标的权重向量ω,然后计算出属性的重要性矩阵、属性权重及专家权重。

2.2 基于阈值理论的废弃矿井抽水蓄能初步筛选模型

我国废弃矿井数量庞大,无法对每处矿井进行细致筛查。本文提出了一种基于阈值理论的初步筛选模型。通过模型初步筛选出来的废弃矿井在下一阶段进行决策、排序,最终找出最适合的废弃矿井。常规抽水蓄能电站选址常把水位差、长高比、水源等作为初始条件,满足所给定的范围才能初步筛选为电站站址的候选地点。

本文结合常规抽水蓄能电站初选因素与矿井构造,确定矿井深度、矿井与城市距离、地下空间、巷道长度、备选方案与电网距离为初步筛选的5 个因素。并在5 个关键性指标的基础上确立了废弃矿井筛选公式。将这5 个指标的临界值设定为标准值,备选矿井的相对应条件与标准值的比值定义为式(1)中的乘积因子,即

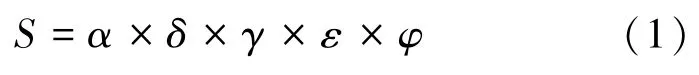
式中,α为备选矿井深度Di与标准矿井深度Ds的比值;δ为备选矿井与城市距离Si与标准矿井与城市距离Ss的比值;γ为备选矿井地下空间Mi与标准矿井地下空间Ms的比值;ε为备选矿井巷道长度Li与标准矿井巷道长度Ls的比值;φ为备选矿井与电网距离Ei与标准矿井巷道长度Es的比值。

式(1)适用于废弃矿井作为抽水蓄能电站的初步选择,得分较高的废弃矿井可进行下一轮细选,最终得到最优站址矿井。

2.3 基于三角模糊数TOPSIS 群决策的选址决策分析模型

本选址决策问题基于模糊判断矩阵阐述该模型的计算过程,本研究选取了22 个指标进行专家打分,确定对选址影响较大的几个因素,建立指标体系。通过模糊多准则决策方法将这几个影响因素与备选地点相结合进行评估和排序。有一些属性的测量难以定量化,对方案在该属性上的表现进行打分时,无法获取定量数据,因此需要专家的主观评判。由于专家研究领域的差异,需对专家进行权重分配。根据专家所给出的判断矩阵,能够求出判断矩阵的一致性程度,一致性程度越高,表明专家思维一致性水平越高,应赋予较高的权重。

本研究采用基于相对距离的专家权重确定方法,步骤如下:

(1) 利用AHP 方法对每位专家的判断矩阵Bk求得赋权向量。

(2) 构造判断矩阵的完全一致判断矩阵B*k=。

(3) 计算各专家判断矩阵Bk与其相对应的一致性判断矩阵B*k的每行差距

(4) 对进行归一化处理:

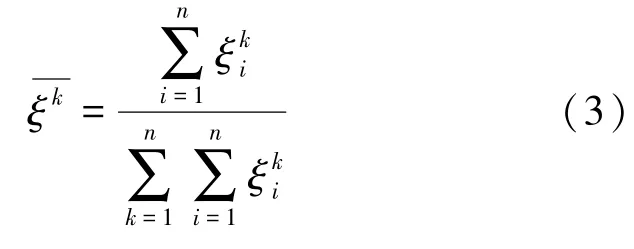
式中,为基于相对距离计算得到的各专家判断矩阵与其相对应的一致性判断矩阵的差异程度。

值表示该专家判断矩阵的一致性程度的高低,其值越大,一致性程度越低,专家赋权就越小。

(5) 利用式(4)确定专家的权重:

式中,为基于一致性判断矩阵的专家权重。

能够反映专家打分意见的一致性越大,表示这位专家在决策中拥有更多的话语权。

本研究对22 个指标因素打分,要求专家基于指标因素对本决策问题的重要度直接打分,采用德尔菲法经过反复征询专家意见,检验判断矩阵一致性。通过一致性检验后,运用AHP 计算出各指标的相对权重(表2)。根据得出的权重结果,选取权重较大的7 个因素,再将选取的决策因素与备选地点进行专家打分,将5 个专家的打分结果与专家的权重相结合,得到集结三角模糊数评价矩阵。

表2 各指标相对权重Tab.2 Relative weight of each index

多属性群决策问题中备选方案集为A={A1,A2,…,Am},Ai表示第i个备选方案;评价属性集为C={c1,c2,…,cn},cj表示第j个属性;ω={ω1,ω2,…,ωn}表示属性的权重向量,ωj为属性cj的权重或者相对重要程度,满足ωj≥0 且e2,…,es}表示决策专家群体,ek为第k个专家;专家ek针对每个备选方案在所有属性上的表现,按照表3 规则进行打分,结果见表4。

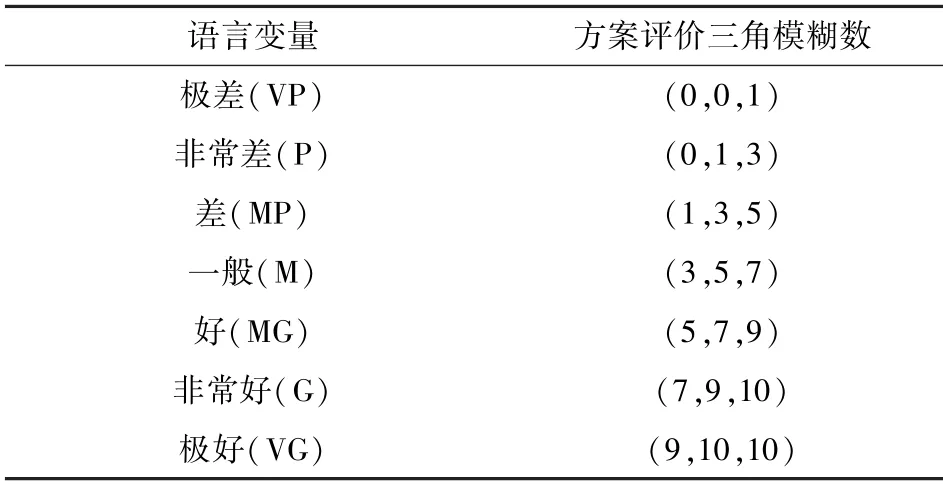
表3 指标评价语言变量的三角模糊数对照表Tab.3 Comparison table of triangular fuzzy numbers for evaluating linguistic variables

表4 决策者ek 方案打分表Tab.4 Scoring table for scheme of decision maker ek

对s个矩阵集结,得到三角模糊数矩阵Dk=(xij)m×n。方案Ai在属性cj上的评分集结可以得到s个评价值,利用各专家自身权重乘对应的评价值再求和,得到初始集结三角模糊数矩阵D=(xij)m×n。

式中,ωk为第k位专家的权重,k=1,2…s,i为备选方案,j为属性。

将集结矩阵中每个元素乘以相对应的属性权重,得到加权集结三角模糊数矩阵

式中,ωj为第j个指标的权重。

备选方案Ai到正负理想解的距离分别记为和,有

利用式(7)、式(8)计算所有备选方案对模糊正理想解的相对贴近度CCi并排序,CCi值最大的即为最优方案。

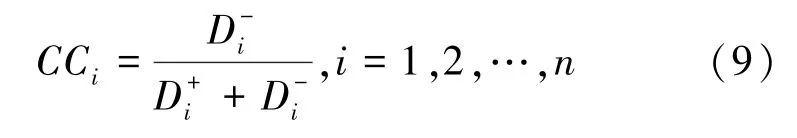
3 废弃矿井抽水蓄能选址实例分析

现有A1,A2,…,A7共7 处矿井(表5)作为研究对象,记为A=(A1,A2,…,A7),每个方案有8 个指标组成指标集,记为C=(c1,c2,…,c8);每个评价指标的权重为ω=(ω1,ω2,…,ω8);5 位专家依据表3 进行评价,记为E={e1,e2,…,e5}。将专家打分表中的备选矿井与因素语言评价值转化为对应的三角模糊数,对方案评价信息进行集结,得到模糊集结矩阵R。

表5 废弃矿井抽水蓄能备选地点与决策因素Tab.5 Alternative locations and decision factors of pumped storage in abandoned mines

(1) 根据专家打分表,利用AHP 方法计算每位专家的排序向量ωk。

ω1= (0.44,0.07,0.05,0.17,0.27)

ω2= (0.43,0.06,0.12,0.15,0.24)

ω3= (0.41,0.07,0.14,0.14,0.24)

ω4= (0.24,0.08,0.06,0.13,0.49)

ω5= (0.32,0.08,0.14,0.17,0.29)

(2) 构造相应专家判断矩阵的完全一致判断矩阵B*k。

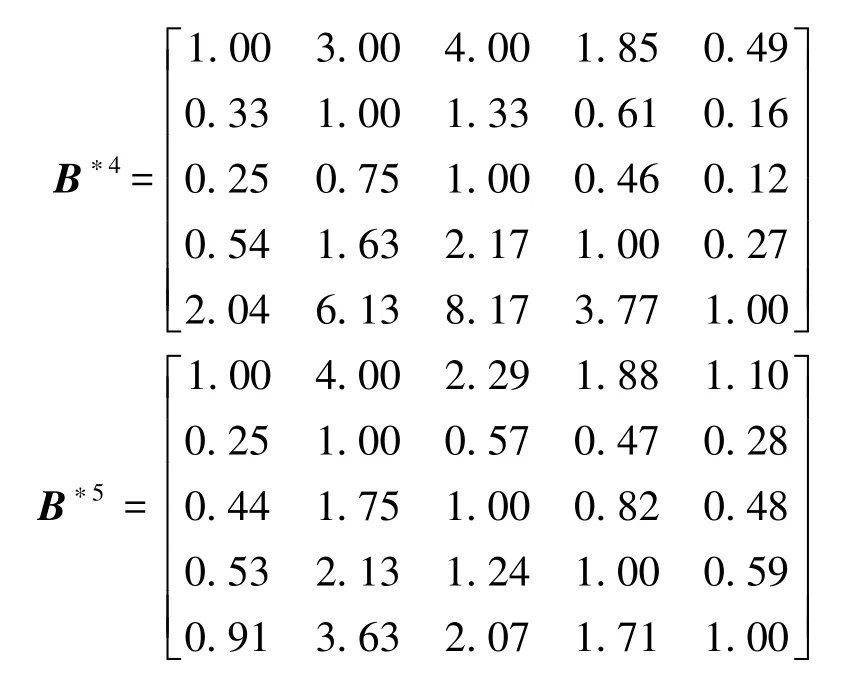
(3) 求解出各专家的权重。ω1=0.212,ω2=0.213,ω3=0.132,ω4=0.228,ω5=0.215。

结合各专家权重,对专家评价进行集结,可以得到集结后的三角模糊决策矩阵D与模糊集结指标因素的权重向量ω。

ω= [(0.74,0.88,0.97), (0.63,0.78,0.91), (0.47,0.62,0.77), (0.39,0.54,0.69), (0.81,0.94,1.00),(0.55,0.70,0.84),(0.35,0.50,0.61),(0.55,0.70,0.84)]

对D进行规范化处理得到标准决策矩阵D′,标准决策矩阵D′与属性权重向量ω模糊集结即得到模糊加权决策矩阵Dl。

利用式(7)和式(8),分别计算到正负理想解的距离和:

根据式(9)计算所有备选方案对模糊正理想解的相对贴近度CCi并排序。

由相对贴近度CCi可以得出,废弃矿井抽水蓄能选址决策的优先度排序如下:

A7> A1> A3> A2> A4> A5> A6

4 结果分析与讨论

4.1 废弃矿井选址因素重要性分析

本研究邀请5 位专家进行指标因素的重要性打分,对每位专家的打分表进行处理,引入一致性比率CR<0.1 进行专家打分表的一致性判断,对于没有满足这一条件的打分表,反馈给专家对打分表进行修改,直至满足要求。经过多轮次反馈,利用MATLAB 计算特征向量及特征值,继而可以计算出通过一致性检验的专家打分矩阵和权重大小。

利用专家打分方法,综合各专家意见,确定了对本选址问题影响较大的指标因素。其中,水位差、地下空间、地质条件、地下围岩支护稳定性、地震类别等因素对废弃矿井抽水蓄能电站的选址影响较大。水位差对于抽水蓄能电站尤为重要,抽水蓄能系统即是将水的重力势能转化为电能,在一定范围内,水位差越大越好。我国机组额定水头最高的抽水蓄能电站为三峡集团浙江长龙山抽水蓄能电站,该电站额定水头高达710 m。废弃矿井抽水蓄能电站的水位差即对应于矿井的地下空间高度,对于本研究至关重要。研究废弃矿井下建造抽水蓄能电站,地下空间也是一个不可忽视的因素,要求能够容纳整个抽水蓄能电站系统。同样,地质条件和围岩支护稳定对于整个发电系统的稳定运行较为重要。

本研究专家打分结果与抽水蓄能电站的常规选址条件一致,因此本打分结果可用作废弃矿井抽水蓄能选址的指标因素。

4.2 专家权重结果分析

本研究中的专家4 的权重最大,即专家4 有更重的话语权,对本选址问题的研究有较大的影响。从结果来看,专家1、2、5 的权重接近,但是专家3的权重最低且与另外4 位专家的权重相差较大,即对本研究影响较小。考虑每位专家的差异,后续对备选地点的排序研究,需要综合各位专家的权重,使得研究结果更合理与准确。

4.3 废弃矿井抽水蓄能站址模糊排序

实证分析结果表明:排序决策的关键性指标分别为矿井水量、水位差、与电网的距离、地下空间、地震发生频率、地下围岩支护稳定性和当地用电量。矿井水量决定是否需从外界引水,决定了抽水蓄能电站的运行成本;水位差在抽水蓄能电站中决定储能的多少;与电网的距离为抽水蓄能电站接入电网正常运行提供了可能。这与其他同类研究的结论高度一致[37]。在关键性指标中,自然因素占比最大,包括矿井水量、水位差、地下空间;其次为安全因素,有地震发生频率和地下围岩支护稳定性;最后为经济因素及社会因素,分别为与电网的距离和当地用电量。

利用三角模糊TOPSIS 决策方法可以得出本研究中备选矿井的优先排序,即通过本决策模型计算出的最优矿井为石圪节煤矿。此井田位于山西长治市北32.5 km,井田面积约15.6 km2,交通条件较为方便。地层走向呈南北,倾向西,倾角平缓,多在3° ～6°之间,呈一单斜构造。井田内最大高差469 m,相对高差350 ～400 m。在全国煤炭去产能政策下,石圪节煤矿作为首批废弃退出的矿井之一,建立抽水蓄能电站对当地资源转型、发展老区经济具有十分重要的意义。