MPAS动力框架和伴随模式简介以 及未来扩展和应用
2021-11-06邹晓蕾
邹晓蕾
(南京信息工程大学 资料同化和应用联合中心,南京 210044)
0 引言
跨尺度大气预报模式(MPAS-A)具有最先进的新动力框架,适用于天气和气候研究。它在非结构球面细分质心Voronoi(SCVT)网格上求解一组完全可压缩的非静水压大气控制方程,在所有模式垂直面上都采用了C网格交错离散方法。MPAS-A SCVT网格主要由不规则六边形组成,对地球球体进行准均匀细分,并在需要时对目标区域进行局部细化。在后一种情况下,网格大小从高分辨率目标区域逐步变化到远离目标区域逐步的粗分辨率区域。这是一种比传统的用于区域模式的单向和双向网格嵌套(譬如天气研究和预报(WRF)模型)更有效的网格细化策略。MPAS-A由若干选定的物理套件组成,这些物理套件中的参数化方案与WRF模式中的相似但不完全相同。
MPAS-A是一个独立的模式,带有前、后处理器。它于2018年5月11日对外公布。由于MPAS-A独特的SCVT变网格,开放性、规范性、科学性、先进性和兼容的WRF物理过程参数 ,选择其发展一个未来先进的全球跨尺度四维变分(4D-Var)资料同化系统。第一步是建立MPAS-A绝热部分的切线线性模式和伴随模式。MPAS-A切线线性模式和伴随模式允许在当前计算机上有效地计算任何4D-Var代价函数相对于极大维数模式初始条件向量的梯度。对于模式预测的敏感性研究,奇异向量集合预测以及涉及正规模态和伴随模态的动力不稳定性和可预测性研究,伴随模式亦是一个有用的工具。
1 MPAS-A 控制方程
MPAS-A动力框架由一组定义在地形追随垂直高度坐标下的完全可压缩的非静力大气模式方程组成。模式垂直坐标面的高度定义为:
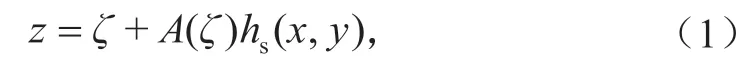
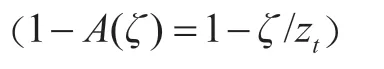
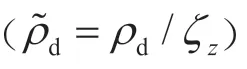
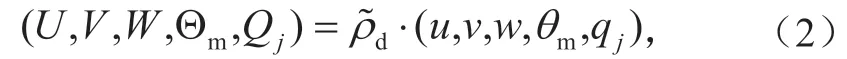
ρ
是一个守恒量,以ρ
定义通量变量,为其他守恒变量建立通量形式的方程,不会引入额外的项。在方程(2)中,u
、v
和w
分别表示两个正交的水平速度和一个从地球中心径向向外的垂直速度;q
、q
、q
、q
等表示湿物质,如蒸汽、云水、雨水和霰等的混合比;θ
是一个由下式定义的修正湿位温:
使用通量变量定义的MPAS-A可压缩非静力大气控制方程表示如下:
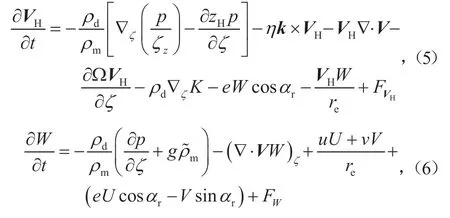

2 伴随模式在求解4D-Var问题中的作用
不同类型观测仪器在不同的时间和时间间隔上进行测量。要在某个分析时间获得对大气状态变量的“最佳”估计时,4D-Var是要求这个大气状态变量的“最佳”估计,作为初始条件得到的数值天气预报模式的模式大气状态预报值与相同时间的观测值差距最小。可以象征性地把任何一个数值天气预报模式写成如下形式:


3 MPAS-A数值离散方案
使用MPAS-A中的SCVT网格对地球球面进行离散化。“Voronoi”一词意味着每个网格单元C
与生成点x
存在这样的唯一相关关系,位于C
中的所有点都比其他任何点更接近x
,并且x
是生成C
的质心。此外,连接两个相邻网格单元的生成点的线垂直并平分两个单元共享的边。与任何结构网格相比,跟踪非结构SCVT网格都更具挑战性。在MPAS-A中可以跟踪下述三种类型的网格元素确定网格单元:1)网格单元中心位置,即Voronoi网格的生成点;2)网格单元顶点位置;3)网格单元的边的位置,即连接两个相邻网格单元中心的线与该边相交的点。根据240 km分辨率下的MPAS-A准均匀非结构SCVT网格分布(图1)和网格单元中心、顶点和边的编号(图2~图4),全球球面被12个五边形和连接任意2个五边形的最短距离曲线(15个六边形网格单元)准均匀地划分为20个等边三角形(图1)。在每个等边三角形中,都有六边形网格单元。12个五边形网格单元的编号依次为0~11。 3个网格均匀分布在20个等边三角形的30个边上,这90个网格的编号依次为11~101。在20个等边三角形中,每个三角形内有3个网格单元,编号依次为102~161。编号为162~641的网格依次位于网格1~161的任意2个网格之间(图2b)。然后将围绕前161个单元的单元从642编号到1601,最后将剩余单元从1602编号到2561(图2c)。可以注意到,随着网格数量从161(图2a)增加到641(图2b),再增加到2561(图2c),网格分布在全球范围内是均匀的,分辨率逐渐增加。顶点按网格单元编号顺序逐个编号(图3)。网格的边的编号从南极增加到北极(图4)。图5给出了MPAS-A可变分辨率网格分布示例,该示例在青藏高原上具有网格细化。网格分辨率从最高的25 km分辨率(在88°E,30°N附近)逐步降低到远离青藏高原地区的92 km左右的较粗分辨率。

图1 240 km分辨率下准均匀MPAS网格的全球分布 (有五条边的单元格以灰色阴影显示;任意两个五边形之间的最短距离(黑色曲线)经过15个网格单元的中心) Fig. 1 Global distribution of the quasi-uniform MPAS grid at a resolution of 240 km (Cells with five sides are shown in shades of gray, the shortest distance between any two pentagons (black curve) passes through the center of the 15 grid cells)

图2 网格单元的全球分布 (a)0~101(红色)和102~161(蓝色);(b)162~641(绿色);(c)642~1601(黑色)和1602~2561(灰色) Fig. 2 Global distribution of grid cells (a) 0~101 (red) and 102~161 (blue), (b) 162~641 (green), (c) 642-1601 (black) and 1602~2561 (grey)

图3 网格单元格及顶点序号 (对于网格单元格0~101的顶点序号为0~599(红色);网格单元102~161的顶点序号为560~959(蓝色);网格单元162~641的顶点序号为960~3839(绿色);网格单元642~1601的未编号顶点序号为3840~4799的全局分布(黑色);对于网格单元1602~2561的未编号顶点序号为4800~5619(灰色)) Fig. 3 Grid cells and vertex sequence numbers (vertex numbers for grid cells 0-101 are 0-599 (red), vertex numbers of mesh cells 102-161 are 560-959 (blue), vertex numbers for grid 162-641 are 960-3839 (green), vertex numbers of 642-1601 are 3840-4799 (black), for the unnumbered vertices of grid cells 1602-2561, the serial number is 4800-5619 (gray)
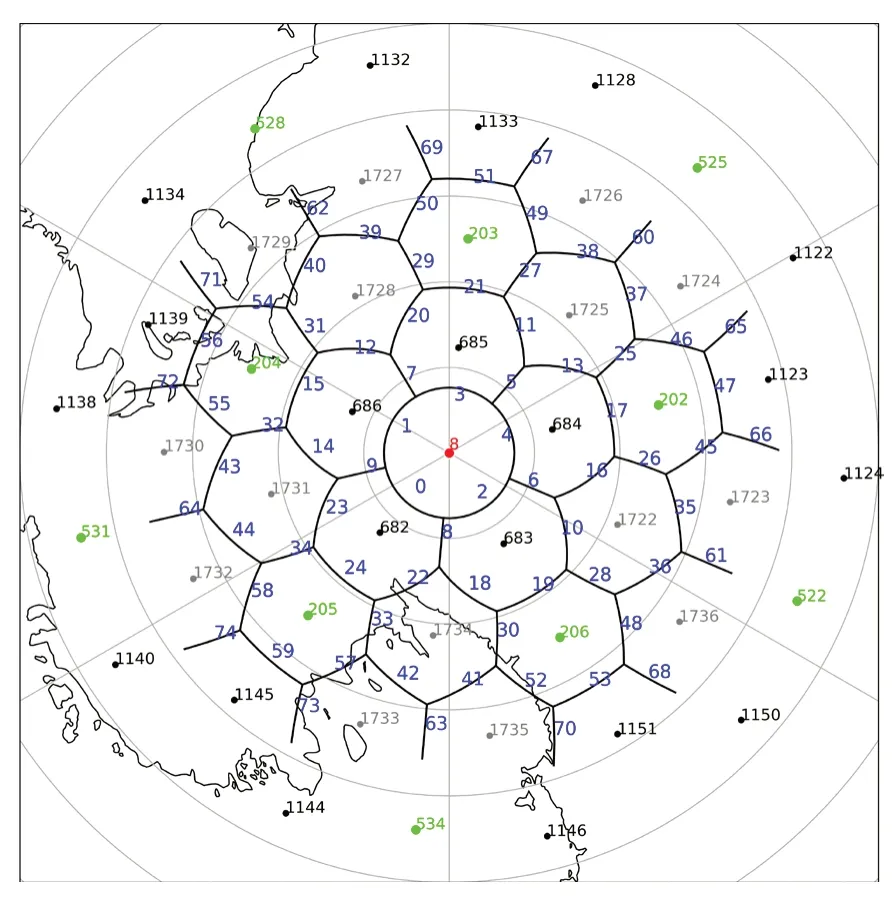
图4 网格边编号为0~74(蓝色) Fig. 4 Grid edges numbered 0-74 (blue)
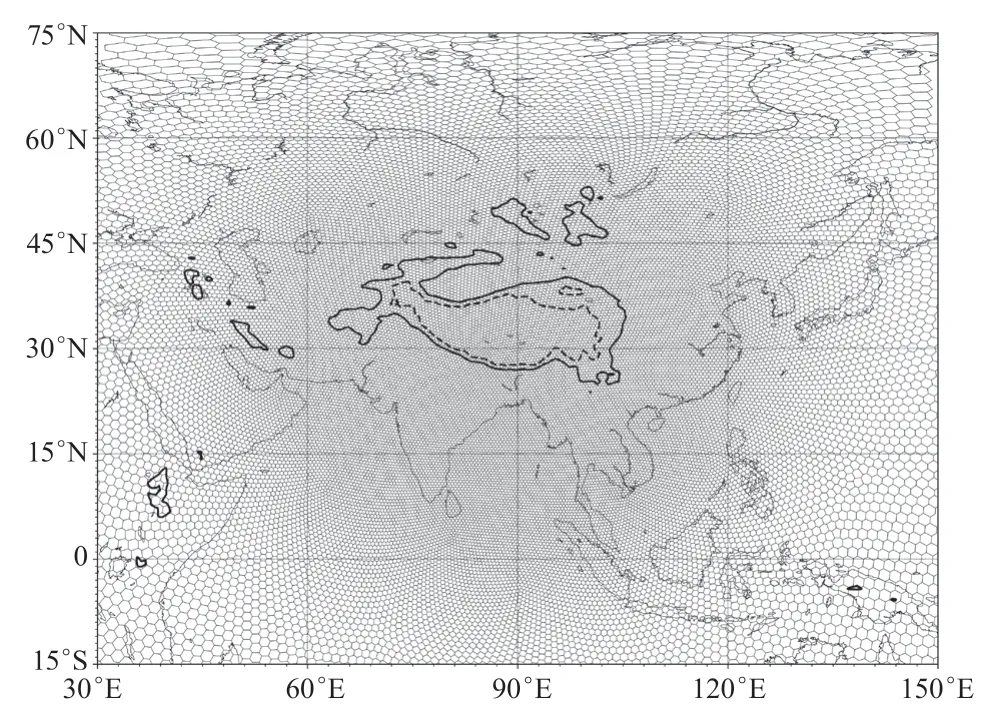
图5 可变分辨率网格单元分布 ((88°E,30°N)附近分辨率最高,为25 km;最粗分辨率为92 km,位于远离青藏高原地区;图中还显示了2000 m(实线)和4000 m(虚线)处的地形高度) Fig. 5 Variable resolution grid cell distribution ((88°E, 30°N) has the highest resolution of 25 km, the maximum coarse resolution is 92 km, located far from the Qinghai-Tibet Plateau, the figure also shows the terrain height at 2000 m (solid line) and 4000 m (dashed line))
MPAS-A在所有模式垂直层上把连续方程(5)~(9)在非结构SCVT网格上实现离散近似表达。C网格交错差分法把法向速度分量(u
)放置在网格边上,并将其他大气状态变量(即密度、湿空气位温、比湿度等)放置在网格中心。C网格交错差分法最初是为具有恒定科里奥利参数的有限差分浅水模式开发的,把它应用到全球SCVT网格不是一个简单的问题。若对包含有网格边上的切向速度的科里奥利项进行简单的离散化,会使地转模态变成不定常的,从而产生虚假数值解。Thuburn等解决了这一具有挑战性的问题,他们把网格边上的切向速度,表达为共享该边的两个网格上所有法向速度的加权平均值: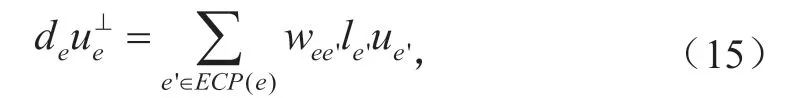



图6 二维浅水模式中预报变量(Φi,ue)和诊断变量 (δi,ξv,ue)的位置定义 Fig. 6 Predictive variable (Φi,ue) and position definition of diagnostic variable (δi,ξv,ue) in two-dimensional shallow water
MPAS-A垂直网格是结构化的。垂直速度定义在垂直速度w
层上,其几何高度由数组“zGrid”提供。其他变量定义在位温θ
层上,其位于相邻两个w层的中点。MPAS-A模式采用龙格-库塔时间积分方案,在一个时间步长内对时间倾向项进行三次更新。在满足库兰特数 条件下,中心平流格式和迎风平流格式都是稳定的。MPAS-A使用了Klemp 等开发的分裂显式积分技术来提高计算效率,即把低频物理模态在一个时间步长 上进行积分,再把每个时间步长 内分成若干较小(声波)时间步长( ),在较小时间步长上对与声波传播有关的项进行积分。4 MPAS-A伴随数值模式及其在敏感性研究中的应用
为了发展MPAS-A伴随数值模式,首先从MPAS-A中分离出MPAS-A的动力框架。然后使用Python驱动程序解析名称列表、操作矩阵、控制模拟时间流、读取模式输入和输出模式预报。最后,为了保证计算效率,保留了MPAS-A的Fortran程序,进行大计算量的模式积分。在此基础上,发展了MPAS-A绝热模式的切线线性模式和伴随模式,并以Jablonowski和Williamson斜压波为例验证了这两个模式的正确性。MPAS-A伴随模式适用于准均匀和变分辨率非结构SCVT全球网格。Zou成功地将MPAS-A伴随模式应用于相对敏感性研究,展示了地面气压预报对模式初始场的相对敏感性分布,详情和数值结果见Zou的研究。类似的研究可应用于其他模式预报量。
5 未来计划
发展MPAS-A切线线性模式和伴随模式,只是朝着开发先进的MPAS-A 4D-Var全球同化系统这个最终目标所做的初步努力。下一步将会发展物理参数化方案的伴随算子,包括积云参数化、行星边界层参数化和微物理过程参数化,并构建背景误差协方差矩阵B
。此外,后续将把飓风涡旋初始化和卫星资料同化等先进科学技术引入到该系统中。在MPAS-A 4D-Var全球同化系统中,还将逐步增加创新组件,包括跟随多卫星轨道的多个资料同化子系统、分等级天气尺度感知同化策略、图像同化新技术以及机器学习等。MPAS-A 伴随模式还可用于其他研究,譬如优化尺度感知的物理参数化方案,集合预报奇异向量以及大气动力不稳定性和可预报性研究。