介质工作参数对板叠上热量搬移效果影响的研究

汪建新 李 萌

(内蒙古科技大学机械工程学院 包头 014010)

1 引言

随着世界经济高速发展,人类对能源的需求与能源供应之间产生供求关系不平衡。环境保护在社会发展中越来越受到重视,人们开始向新型能源和节能技术等领域拓展。在开发新能源、寻求新技术的不断探索中,热声效应研究是一块非常重要的内容,其中热声制冷技术更是制冷领域的新型前沿学科。热声制冷机的核心部件是板叠,板叠上气体与板叠的换热特性是重点研究方向,该研究对进一步提升热声制冷机的制冷效率有重大意义。同时,工作参数对换热的影响同样重要,包括声波频率、振幅以及板叠材料等。

在国内外相关研究中,大多通过试验对换热特性进行探究,而试验结果的准确性又受到试验器材、试验场所及人为等因素影响。本文以数值模拟和试验探究相结合的方法研究这一问题,以数值模拟的方法建立微气团在循环周期内发生温度变化、与固体板叠进行热量交换的模型,详细分析振动制冷过程中任一时刻的温度及热量变化。选择合适水平及正交表进行仿真试验,统计分析板叠两端温差的大小,探索各工况参数之间的最佳组合,为提高工作效率提供参考。通过搭建试验平台进行试验探究,在对试验结果分析之后和数值模拟结果比对,把握各参数对制冷效果的影响,为改善制冷效果提供努力方向[1-2]。

2 物理模型简化及有限元模型建立

首先是物理模型的建立。为使模型简化而又能说明问题,在课题组前期研究基础上可知,因板叠结构对称,在两板之间气体的运动、对上下板能量交换也为对称的,因此选取一个气体微团及其周期运动范围内的单片板叠作为分析对象[3],当改变物理参数及工作参数时,研究各因素对热量搬移效果的影响,在ANSYS 软件中建立数值模型。物理模型由两部分组成,上方的空气柱以板叠间隙形状为基础,为保证气体在振动过程中完全作用在板叠上,长度必小于板叠,厚度取为板叠间隙宽度的一半,将其简化成长方体。下方同为简化成六面体的板叠,仅取这一个空气微团作用范围内的板叠长度,所以二者同宽度。具体参数如下,板叠长40 mm,间隙4 mm,板厚2 mm,宽度10 mm。空气柱长20 mm,厚度2 mm。整体完成网格划分后形成的有限元模型如图1 所示。

图1 网格划分图Fig.1 Grid map

3 热量搬移效果影响因素的数值正交试验

3.1 正交试验设计

影响热声制冷效果的因素有许多,若考虑所有相关参数和参数之间各级交互作用效应的大小,将要进行庞大数量的计算。在课题组前期的研究基础上,选取声场频率(A)、振动幅值(B)和板叠的材料(C)为试验因素,形成的温度梯度大小为试验指标进行数值正交试验[4-5]。每个试验因子都取4 个水平,首先是频率水平的选取。先对放置了板叠的谐振腔内气体柱做模态分析,以模态振动来替代驻波型振动,因为这两种振动中气体的运动规律是一致的,其次气体发生模态振动的时候,在同等条件下在板叠上形成的温度梯度更加明显,便于观察换热规律。谐振管的尺寸以搭建好的试验平台为参考,取内径100 mm,外径110 mm,长度500 mm。为了满足不同频率下对板叠长度和位置的需求,同时不将板叠的长度和摆放位置作为变量考虑,故将板叠设置为管长的一半,为250 mm,如图2 所示。观察可能出现的振型及对应的特征频率,选取活塞模态振型来替代驻波型振动,如图3 所示,激励频率水平分别为346 Hz、693 Hz、1 390 Hz和2 094 Hz。

图2 谐振腔几何模型图Fig.2 Geometric model of resonator

图3 模态振动频率图(1 390 Hz)Fig.3 Modal vibration frequency diagram

振动幅值的数值应该小于气体柱的长度,同时又要保证在仿真结果中体现出明显的影响。考虑到模型的接触部分共用节点,且该长度需要保持为划分网格长度的整数倍,得到振动幅值4 个水平分别为:5 mm、10 mm、15 mm 和20 mm。以导热系数这个最为直观的传热参数为参考,依据导热性能的高低选择了四种板叠材料,在传统传热材料中选择了黄铜与不锈钢,新兴材料中选择了氧化铍陶瓷和石棉。确定各因素水平后安排到所选正交表相应的列中,如表1 所示为L16(43)正交试验水平安排表。

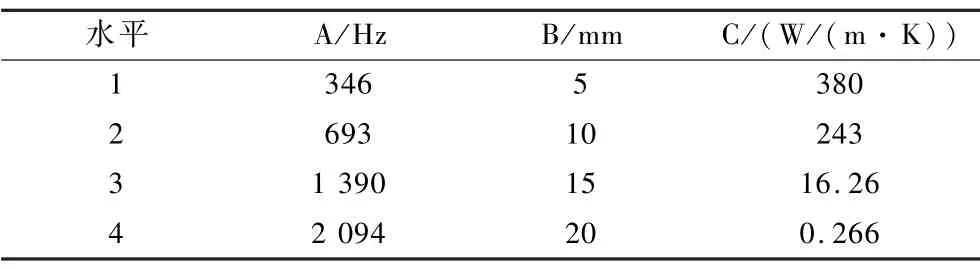
表1 正交试验水平安排表Table 1 Level arrangement of orthogonal test

3.2 载荷的确定与施加

气体在其平衡位置附近进行简谐振动,对气体整体施加位移和温度载荷,位移与时间的曲线为正弦函数x=Asinωt的形式。微气团在平衡位置两侧位移最大处自身温度为极大值和极小值,位于平衡点时温度与板叠温度一致,温度随位移的变化可近似于线性,如图4 所示。将温度随位移变化的函数简化为T=Kx+T0的形式,|K|表示温度随位移的变化率。对低斜率进行多次试验后在板面上得到的温差不显著,且受到最小网格尺寸的限制,无法进一步从结果上放大,因此通过设置|K|为3 000 来放大结果。

图4 制冷循环内板叠上的温度梯度Fig.4 Temperature gradient on stack in refrigeration cycle

气体在位移发生变化时,压力变化,温度也发在生变化,气体在每个位置处与板叠的热量交换过程都需要做瞬态热分析,为此需要将气体运动函数离散化。考虑到网格划分十分精细,计算时间长,重复操作工作量巨大,又要保证结果的精度等因素,在多次试验后确定将一个气体工作循环等分为12 个载荷步,即把气体位移函数中一个波长离散为12 段,载荷施加完成后开始对模型进行求解。

3.3 试验结果分析

气体在板叠上的位移过程如图5 所示。从图中可以直观地看出板叠在变温气体的影响下在板面形成温度梯度的运动过程,灰度代表温度,由深渐变到浅是温度数值增大。气体在进行简谐振动的时候,在每一时刻对板叠产生的影响在板叠内部会发生效果的叠加,因此无论在板面沿声波传播方向,还是法向方向都有温度梯度形成。

图5 气体在板叠上的位移过程图Fig.5 Displacement process of gas on stack

记录结果中板叠上沿声波传播方向上的温度极值,计算温差并记录,具体结果如表2 所示。由表3 可知,试验因子敏感度的排秩为导热系数>振幅>频率。这说明在影响热声制冷效果因素中,板叠材料的选择是优于其它因素的,振幅的调控仅次于材料的选择。在保证前两因素敏感度取到较好水平情况之下,振动频率可在较大范围内选取,为获得大振幅提供了依据。

表2 正交试验结果Table 2 Results of orthogonal test

表3 均值响应表Table 3 Mean response table

数值模拟结果显示石棉材料形成温度梯度最大,故在所选材料中用石棉作为板叠材料最好。振动幅值升高,温度梯度也在增加,这表明在可控范围内幅值应越大越好。虽然同为气体各阶的模态振动频率,但是在振动频率的水平选取范围内出现了转折点。这说明在频率1 390 Hz附近存在最优值,为在所选范围内得到更好的制冷量,后面将以频率为变化因子做单因素试验。关于因子水平的优劣可以由图6 直观的表示出来,最佳因素水平组合为(A3B4C4)。

图6 均值主效应图Fig.6 Mean main effect plot

为验证使用正交试验分析出的最佳因素水平组合(A3B4C4)这一结果的正确性,按照最佳因素水平的参数对程序进行修改,得到板叠温度模拟结果如图7 所示,在板叠上表面两端产生的最大温差为85.5636 ℃,这一温差大于在正交试验中得出的任何一组结果,可为提高工作效率提供参考。

图7 板叠温度图Fig.7 Stack temperature diagram

3.4 单因素数值试验分析

基于上述通过正交试验法分析得出的结果,发现在频率水平的选取上应选1 390 Hz,但是在通过ANSYS 对模态分析时存在小范围的波动,故在该点附近寻找最佳的振动频率需要进行单因素试验分析。将其它水平确定为正交结果中各自的最佳水平,即选择石棉材料的板叠和气体振动幅值为20 mm。频率值的选取应用均分法,在1 390 Hz 上下浮动100,间距10 Hz,设置10 组试验,数据及结果如表4 所示。从表4 中不难看出,在1 390 Hz附近的频率中,随着振动频率的增加,板叠上的温差大小是呈周期型波动的。1 350 Hz、1 380 Hz、1 410 Hz 和1 420 Hz 这4 个频率下,出现了大于1 390 Hz 制冷温差的数值。说明在正交试验的最佳振动频率附近的确存在更优点。对比出现在各周期内的温差极值,可以发现即便是温差呈波动变化,其峰值仍处于递增趋势。因此可得出在1 390 Hz 振动频率附近,最优值为1 410 Hz。优化后的因素水平组合为:选择石棉作为板叠材料,且气体振动幅值为20 mm,激励频率为1 410 Hz。

表4 单因素试验结果Table 4 Single factor test results

在以上试验中,把振幅与频率作为独立因素进行考察,发现频率在很宽范围内变化时,对制冷效果影响不大。事实上,气柱振动时存在固定的幅频特性,振幅与频率并不独立,只有在共振点附近才能获得最大振幅。正交试验结果提示,可以把激励频率设置在一阶活塞模态频率上,以获得最大振幅,而不考虑频率变化的影响。

4 试验分析

为了验证数值模拟结果的准确性,通过搭建试验平台进行试验探究,在对试验结果分析之后和数值模拟结果进行比对,把握各参数对制冷效果的影响,为改善制冷效果提供努力方向。

4.1 试验平台的搭建

在进行试验之前,首先要对试验平台进行搭建,平台核心构件是含有平行板叠的谐振腔。考虑到课题组要通过该试验平台进行PIV 试验,谐振腔选择以PMMA 材料制成,因为PMMA 材料透明度非常好,透光率可达92%,便于加工,价格低。板叠在材料选择上以数值模拟中的材料设置为主,使用黄铜、不锈钢及石棉,舍弃了新兴材料氧化铍陶瓷,主要原因是该材料难以进行小规模定制。驱动装置采用扬声器,配备了信号发生器和功率放大器,用来改变声波的频率和激励电流。在板叠两侧放置热电偶,对其两端的温度进行测量,使用温度显示仪器读取温度。搭建完成的试验平台如图8 所示。

图8 试验平台Fig.8 Test platform

4.2 导热系数及振幅对制冷效果影响的研究

通过控制两种参数的改变进行不同工况对制冷效果影响的试验。以扬声器作为驱动装置提供试验所需的声功,声波频率选择346 Hz。在频率确定的情况下通过激励电流的改变调节振幅,激励电流的改变范围是0.3—1.8A,将此范围均分并取6 个数值作为激励电流。对3 种不同材料的板叠进行更换,以寻求介质工作参数改变对板叠上热量搬移效果的影响。使用热电偶对板叠两端的温度测量并记录,每组试验的时间都是10 分钟,绘制关于温差随参数改变后而发生变化的曲线,板叠两端温差变化如图9 所示。由试验结果可知,在相同频率及激励电流的工况下,石棉材料板叠两端产生的温差数值最大,其数值整体高于黄铜材料板叠与不锈钢材料板叠产生的温差,试验结果中制冷效果最差的是不锈钢材料板叠。这种不同导热系数的材料板叠对温差的影响趋势与数值模拟结果相吻合,在选择的材料中,石棉材料板叠制冷效果最好。关于改变激励电流调节振幅对制冷效果影响的趋势是振幅越大,制冷效果越好,3 种板叠材料的温差变化曲线都是随着激励电流的增加在不断升高,这种变化趋势同样与数值模拟结果相同。通过试验探究分析并结合数值模拟结果,得出石棉材料是所选择材料中产生温差效果最好的材料,不同导热系数对温差的产生有较大影响,而振幅对温差的影响趋势是越大越好,结论可以为热声制冷机的参数优化及改善制冷效果提供参考。

图9 板叠两端温差变化图Fig.9 Variation of temperature difference at both ends of stack

4.3 频率对制冷效果影响的研究

在数值正交试验中,把振幅与频率作为独立因素进行考察,发现频率在很宽范围内变化时,对制冷效果影响不大。为探究频率改变对制冷效果的影响,选取4 个活塞模态频率:346 Hz、693 Hz、1 410 Hz、2 094 Hz和4 个非活塞模态频率:470 Hz、960 Hz、1 050 Hz、2 500 Hz,板叠材料为制冷效果最好的石棉,激励电流为0.9A,在此工况下进行试验,每组试验进行10 分钟,对板叠两端的温度数值记录,结果如表5 所示。由表5 可知,活塞模态频率在较大跨度内变化时,对产生的温差数值变化影响非常小,且使用活塞模态频率产生的温差数值远大于使用其它频率产生的温差数值。说明气柱振动时存在固定的幅频特性,振幅与频率并不独立,只有在共振点附近才能获得最大振幅,而活塞模态频率在很宽范围内变化时,对制冷效果影响不大。

表5 不同频率下板叠两端的温差Table 5 Temperature difference between two ends of stack at different frequencies

5 结论

(1)通过数值模拟的方法建立微气团在循环周期内发生温度变化、与固体板叠进行热量交换的模型,全面考虑各因素的影响效果,选取数值正交试验法,探索各工况参数之间的最佳组合。结果说明对制冷过程影响最大的因素是板叠材料的导热系数,其次为气体微团的振幅,影响最小的是振动频率,在保证前两因素敏感度取到较好水平情况之下,振动频率可在较大范围内选取,为获得大振幅提供了依据。最佳因素水平组合为(A3B4C4),即频率为1390 Hz、板叠材料为石棉、振幅为20 mm。在数值模拟试验中把振幅与频率作为独立因素进行考察,发现频率在很宽范围内变化时,对制冷效果影响不大。正交试验结果提示,可以把激励频率设置在一阶活塞模态频率上,以获得最大振幅,而不考虑频率变化的影响。

(2)通过搭建试验平台进行试验探究,在对试验结果分析之后和数值模拟结果进行比对,得出石棉材料是所选择材料中产生温差效果最好的材料。不同导热系数对温差的产生有较大影响,而振幅对温差的影响趋势是越大越好。活塞模态频率在较大跨度内变化时,对产生的温差数值变化影响非常小,且使用活塞模态频率产生的温差数值远大于使用其它频率产生的温差数值。说明气柱振动时存在固定的幅频特性,振幅与频率并不独立,只有在共振点附近才能获得最大振幅,而活塞模态频率在很宽范围内变化时,对制冷效果影响不大。