基于滑动窗口模型的数据流闭合高效用项集挖掘
2021-11-05程浩东李小娟
程浩东 韩 萌 张 妮 李小娟 王 乐
(北方民族大学计算机科学与工程学院 银川 750021) (734811467@qq.com)
高效用项集挖掘(high utility itemset mining, HUIM)是一项经过广泛研究的数据挖掘任务[1],它通过考虑一些其他因素扩展了频繁项集挖掘(frequent itemset mining, FIM)[2].FIM仅将项集出现的频率作为其在数据库中的重要性度量,不考虑每个项目的效用价值.但是,HUIM则同时会考虑项目的效用或实用价值.在高效用项集挖掘领域,交易事务中物品的数量称为内部效用,项目的利润被称为外部效用.项目的效用被定义为物品数量和利润(即内部效用和外部效用)的乘积.挖掘高效用项集(high-utility itemset, HUI)的问题可以描述为找到所有效用值大于或等于用户自定义阈值的项集,这个阈值称为最小效用阈值(minutil).较早的算法[3-6]被设计为在2个阶段挖掘高效用项集,其后又引入1阶段算法[7-14].
高效用项集在市场篮分析、产品推荐等实际应用中效果显著,但静态数据库的高效用项集包含了旧数据的影响.近年来,无线传感器网络、零售市场交易、通信网络和网站在线点击等场景都在生成数据流.挖掘来自数据流的项集更加有用,因为它包含基于最新数据且不受旧数据影响的项集或模式,用户可快速获取相关信息以采取适当的措施.例如,考虑在企业环境中部署多个WiFi接入点的场景[15],HUIM可以用于该网络中的实时负载均衡.每个事务被建模为一天中访问点的使用情况,其中将访问点定义为项目,并且将连接到其的客户端负载表示为访问点的内部效用,将数据传输到服务器的成本定义为与其关联的外部效用.访问点的效用可以定义为负载和成本的乘积,近而实时识别高负载访问点集,此类信息可用于负载的重新分配或调控.
文献[16-18]中已经提出了算法用于从数据流中挖掘高效用项集,但这些算法均属于全集高效用项集挖掘算法.全集项集挖掘算法的固有问题是生成大量模式信息冗余的项集,难以被用户理解和运用.因此,一些压缩或紧凑的HUI表示方法被提出.静态高效用项集挖掘领域已提出一种称为闭合高效用项集(closed high utility itemset, CHUI)的概念[19],它的大小比高效用项集全集小几个数量级,且不丢失任何有用信息.相对于比较有限的内存空间,CHUI挖掘能更好地满足用户需求,开展此类挖掘的研究具有重要意义.仍以WiFi场景为例,假设在相同日期内某一区域访问点A和B均处于高负载状态,且{A},{A,B}都是HUI,则{A,B}即为需要挖掘的CHUI.显然该项集减少了冗余信息,在准确识别所有高负载访问点的基础上,后者为企业按区域优化网络配置提供更佳方案,向运营企业提供更有意义的决策信息.现有文献已提出多种有效挖掘CHUI的算法,比如CHUD[19],CHUI-Miner[20],EFIM-Closed[21],CLS-Miner[22]等.而后Dam等人[23]针对动态增量数据库提出新的闭合算法IncCHUI.
类似于静态数据和增量数据,数据流中同样迫切需要进行CHUI挖掘.由于数据流的海量性等特点,造成对于它的挖掘和存储都有一定难度.同时,随着时间的不断推移,用户通常只关注数据流中近期有价值的信息.所以已提出的静态和增量闭合高效用项集挖掘算法并不能直接适用于数据流挖掘任务.
为此,本文设计了第1种基于滑动窗口的数据流闭合高效用项集挖掘算法,以解决数据流全集高效用项集挖掘带来的项集信息冗余问题,而这一主题在此之前尚未被探讨.这项工作的贡献总结为:
1) 提出一个名为CH-List的新颖数据结构,它可以有效地计算内存中项集的效用和支持数,而无需重复扫描原始数据流.CH-List相较于传统闭合EU_List[20],IUL(incremental utility-list)[23]等结构,适用于数据流滑动窗口,在批次的插入和删除方面非常有效.
2) 提出了一种新的融合CH-List结构的算法,即基于滑动窗口模型的数据流闭合高效用项集挖掘(closed high utility itemsets mining over data stream based on sliding window model, CHUI_DS)算法.该算法采用分而治之的思想,通过创新一种事务重组方法以及改进的闭包挖掘技术,近而在数据流滑动窗口中挖掘出完整的CHUI.
3) 对真实数据集和合成数据集进行了广泛的实验研究,以评估所提出算法的性能.实验结果表明:CHUI_DS的总体性能优于目前最先进的相关批处理和增量算法.此外,算法在不同窗口环境下的可扩展性也得到有效验证.
1 相关工作
高效用项集挖掘的缺点是算法返回的结果集数量巨大,这使得分析这些结果集成为一项艰巨的任务,同时它们包含很多冗余项集信息.针对以上问题,Tseng等人[19]提出了一种紧凑且无损的高效用项集表示形式,如果项集的效用不小于用户指定的最小效用阈值,并且不存在相同支持数的真超集,则该项集称为闭合高效用项集.每个CHUI都由一种称为效用单元阵列的特殊结构进行注释,采用这种结构,高效用项集全集得以在无需访问原始数据库的情况下从该集合派生出来,因此CHUI的集合是无损的.另外,研究者提出了第1种发现静态数据库中CHUI的算法,名为CHUD[19],以及一种名为DAHU的方法从完整的CHUI集中恢复所有HUI.Wu等人[20]提出了一种名为CHUI-Miner的新颖算法,该算法依赖Utility-List垂直列表结构以单阶段发现CHUI.通过该结构的剩余效用(remaining utility, RU)属性,可以获得项集超集更严格的效用上限,从而可以较大范围地修剪搜索空间.Fournier-Viger等人[21]提出了一种名为EFIM-Closed的闭合高效用项集挖掘算法.该算法包括3种修剪策略,分别为闭合跳跃、向前闭合检查和向后闭合检查,以修剪非闭合的HUI.此外,它还引入了事务投影和事务合并机制.实验结果表明:与CHUD算法相比,EFIM-Closed运行快1个数量级以上,并且消耗的内存少1个数量级.Dam等人[22]提出一种称为CLS-Miner的算法,应用链估计效用共现修剪、较低分支修剪和按覆盖范围修剪等新颖剪枝策略减少搜索空间,提出的CLS-Miner算法优于CHUD和CHUI-Miner算法.
在增量数据环境中,同样针对上段描述的相关问题,研究者提出IncCHUI[23]算法,其使用增量效用列表结构从数据库中挖掘CHUI.IncCHUI仅扫描原始或更新的数据库1次,以构造单个项的列表.使用称为CHT的散列表存储目前为止发现的CHUI.对于在更新的数据库上挖掘时发现的每个闭合高效用项集P,算法首先检查该项集是否已在CHT中,再决定是否需要将P插入表CHT中.这是目前首个对增量数据库进行闭合高效用项集挖掘的算法.
在数据流上挖掘HUI比在静态或增量数据库中更具挑战性.因为传入的数据流必须在时间和存储内存约束下进行实时处理.目前有3种主要的流处理模型[24-25]:1)阻尼窗口模型;2)地标窗口模型;3)滑动窗口模型.其中窗口是1组连续交易,被视为数据流中的单位.在滑动窗口模型[26-27]中,方法使用固定大小窗口中的最新数据来发现数据流中有意义的项集.该模型因能够强调最新数据并占用较小内存资源而被广泛用于数据流挖掘.为考虑资源受限环境中真实的数据流挖掘任务,Ahmed等人[16]提出了基于滑动窗口的HUIM.为了满足向下闭包特性,早前基于滑动窗口的研究采用了事务加权效用(transaction weighted utility, TWU)高估概念[28],缺点是导致生成大量候选项集,处理这些候选项集需要更多的执行时间.Ryang等人[17]提出一种树结构的高效用挖掘算法SHU-Grow,用于从滑动窗口模型中挖掘HUI.此外,其还开发了2种技术:降低的全局估计效用(reducing global estimated utilities, RGE)和降低的局部估计效用(reducing local estimated utilities, RLE),以取代TWU高估方法来减少搜索空间和候选项集.上述在数据流上挖掘高效用项集的算法是2阶段的.随后Jaysawal等人[18]提出一种有效的单程1阶段算法SOHUPDS来在数据流上挖掘HUI,借助IUDataListSW结构,存储项目在事务中的位置和实际效用,以及可以从项目扩展项集效用上限,它比之前的算法更加有效.
一些工作还提出了在数据流上挖掘HUI的衍生算法.Zihayat等人[29]提出了一种称为HUDS-tree的树状结构,树中每个节点逐批维护高估的效用值.采用基于滑动窗口模型的2阶段算法T-HUDS挖掘前k个HUI,它在第1阶段生成候选的高效用项集,在第2阶段验证项集的确切效用.Dawar等人[15]提出一种称为Vert_top-k_DS的算法,该算法可在不生成任何候选项的前提下挖掘出前k个HUI.其在动态阈值提升策略的基础上,利用k-项集在公共批次的实际效用值增加窗口滑动时的初始阈值,是目前最先进的数据流top-k高效用项集挖掘算法.在文献[30-31]中提出的算法用于在数据流上挖掘高效用序列模式(high utility sequence pattern, HUSP),前者提出的HUSP-Stream是在数据流上查找HUSP的第1种方法,后者提出了一种名为HUSP-UT的新挖掘算法,实验性能大幅优于HUSP-Stream.
2 定 义
设由不同项构成的有限集合I*={I1,I2,…,Im},其中每个项Ii∈I*都与1个正数p(Ii,DS)相关联,称为外部效用.令数据流DS=(T1,T2,…,Ts)是有限事务组成的序列,数据流DS中的每个事务Tr(1≤r≤s)表示第r个到达的事务,其中每个事务Tr∈DS是I*的子集,并且具有唯一的标识符r,称为其Tid.在事务Tr中,每一项Ii∈I*都与1个正数q(Ii,Tr)相关联,在Tr中称为其内部效用(例如购买数量).项集P是由1组属于I*的项{I1,I2,…,Ik}构成的集合,P的长度表示为k,其中P⊆I*且1≤k≤m.
在滑动窗口模型中,每个窗口SWk由固定数量的n个最近的批次组成的有序集合,可以表示为SWk=(Bj,Bj+1,…,Bn),该窗口大小(winSize)为n.批次Bj包含固定数量的事务,即Bj=(T1,T2,…,Tr).窗口SWk-1滑动时,最旧的批次被从窗口移除出去,最新的一个批次将被添加进来,这个新生成的窗口即为SWk.其中Bj+1,Bj+2,…,Bn-1称为SWk-1和SWk的公共批次(CommomBatches).
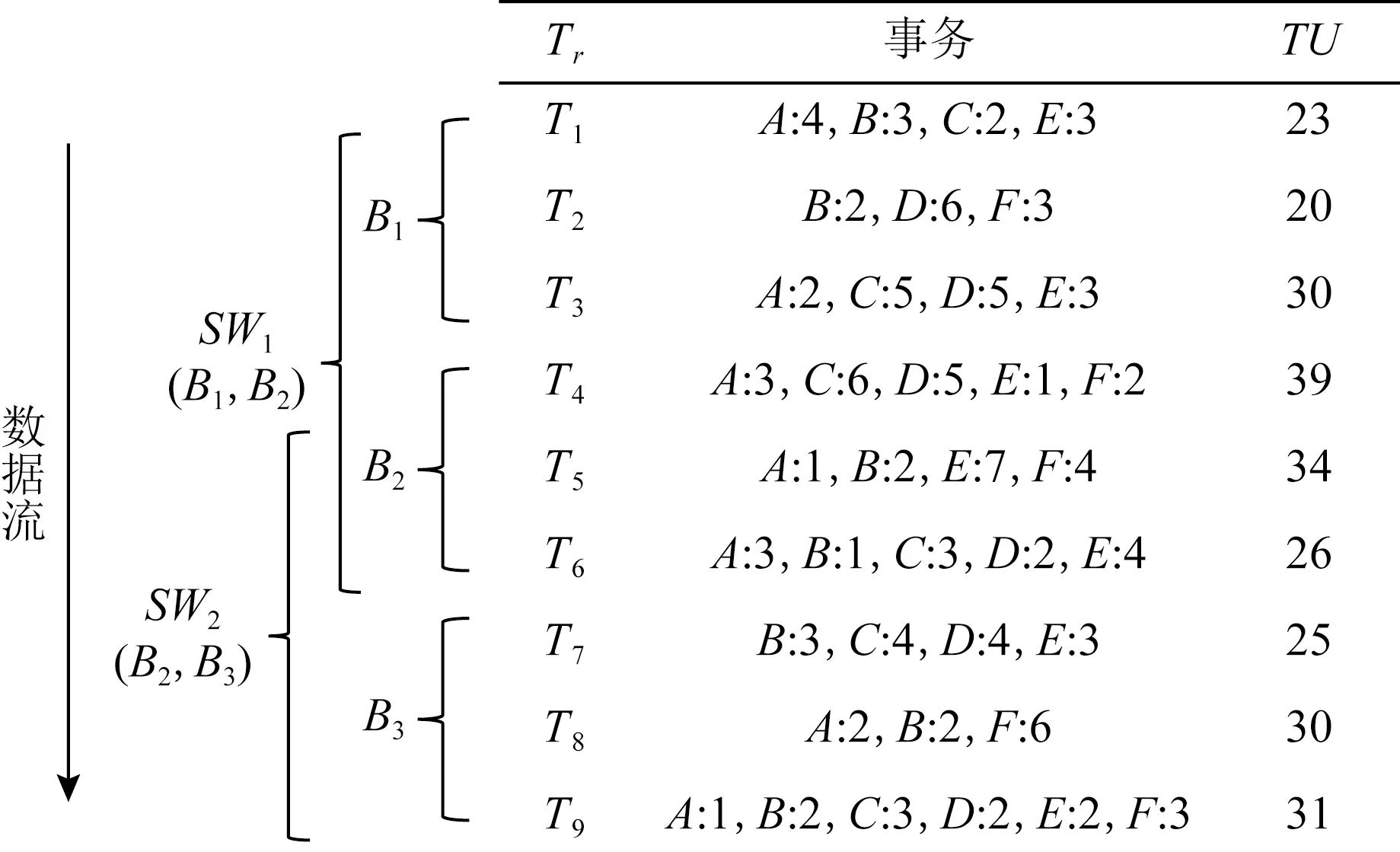
Fig.1 Example of stream data图1 数据流示例
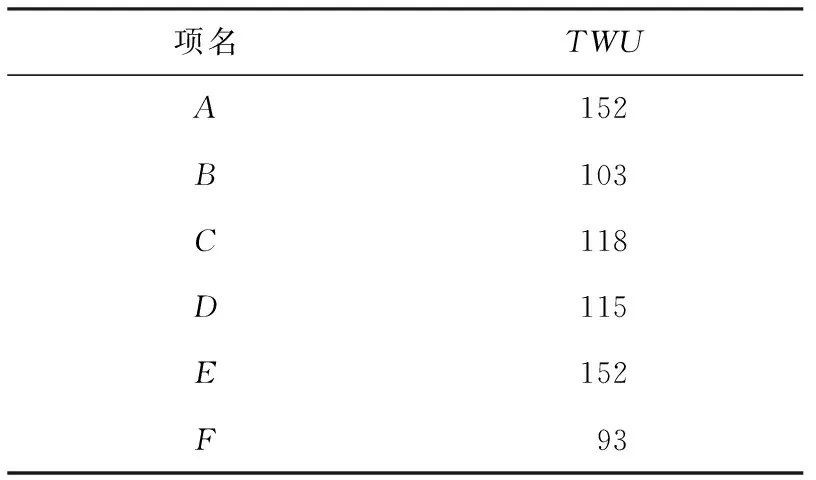
图1显示了一个数据流的示例,示例中的每一行代表1个事务,事务中每个字母代表1个项目,并在右侧附其内部效用.表1列出了每个项目的外部效用.该数据流分为3个批次B1,B2,B3,其中每个滑动窗口由2个批次组成.示例中共存在2个滑动窗口,SW1={B1,B2}和SW2={B2,B3}.在此,SW1是初始滑动窗口.随着新数据的到达,由于第1个窗口已满,通过移除最旧的批次并插入新批次后,SW1更新为滑动窗口SW2.

Table 1 Profit Table表1 外部效用表

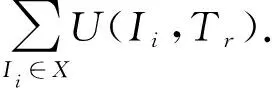
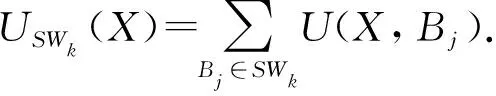
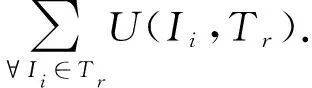
例如,T1的事务效用为TU(T1)=U({ABCE},T1)=23.
定义4.超集和子集.设非空项集X和Y.X是Y的子集,如果X⊆Y,则等效地Y是X的超集.如果X⊂Y,则X是Y的真子集,而Y是X的真超集.

例如,SUPSW1({ACE})=|TidSetSW1({ACE})|=|{1,3,4,6}|=4.
属性1.对窗口SWk中的k项集X,SUPSWk(X)=|TidSetSWk(I1)∩TidSetSWk(I2)∩…∩TidSetSWk(Ik)|.
属性2.对窗口SWk,令项集Y为X的真超集,则有TidSetSWk(Y)⊆TidSetSWk(X).
定义6.闭合项集.如果SWk中不存在真超项集Y⊃X使得SUPSWk(X)=SUPSWk(Y),则项集X在窗口SWk中称为闭合项集.闭合项集的完整集合表示为CSWk.

例如,窗口SW1中,closure({AB})=T1∩T5∩T6={ABCE}∩{ABEF}∩{ABCDE}={ABE}.
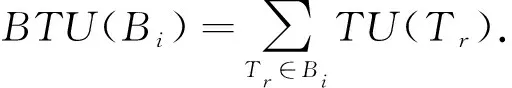
定义9.总效用.滑动窗口SWk的总效用表示为TotalUtility,并定义为
定义10.高效用项集(HUI).如果窗口SWk中的项集X的效用USWk(X)≥minutil,则在SWk中将X称为高效用项集.
例如,窗口SW1中{BE}的效用为USW1(BE)=U(BE,B1)+U(BE,B2)=9+25=34.SW1中事务的总效用为172.若minutil=30.96,则{BE}在SW1中是高效用项集,因为其效用USW1(BE)=34>minutil.
定义11.闭合高效用项集(CHUI).如果项集P是SWk中的高效用项集且满足P⊆CSWk,则P为闭合高效用项集.
属性3.对于任何高效用项集X,都存在一个闭合高效用项集Y,使得Y=closure(X)并且U(Y)≥U(X).
属性4.对于不是闭合高效用项集的任何项集X,其所有子集都是低效用的.
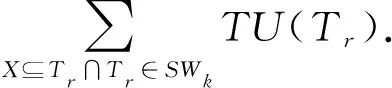
例如,TWUSW1(AC)=TU(T1)+TU(T3)+TU(T4)+TU(T6)=23+30+39+26=118.
定义13[28].事务权重使用率向下封闭(TWDC)属性.对于任何项集X,如果其TWU 定义14.窗口中的高事务加权效用项集.如果TWUSWk(X)≥minutil,则项集X称为窗口SWk的高事务加权效用项集. 属性5[28].使用TWU修剪.假设有一个项集X不是高TWU项集,则X及其超集均是低效用项集. 对于数据流中的滑动窗口SWk,问题是要在SWk中找到所有CHUI,其中minutil是用户定义的参数. 本节提出一种新的效用列表结构CH-List和基于滑动窗口模型的数据流闭合高效用项集挖掘算法CHUI_DS,利用滑动窗口在数据流中挖掘闭合项集是为了在有限的内存资源下从连续数据中及时发现最新的无冗余项集.此外,算法开发了2种技术:基于批次剩余效用表(batch based remaining utility table, BRU_table)的公共批次事务重组方法和减少闭包计算的效用剪枝技术,以通过高估候选闭包项集的效用来减少搜索空间.在描述本节的数据结构之前,先介绍一些术语. 定义18.项集的扩展.设X={x1,x2,…,xv}(Xi∈I*,1≤i≤v)和Y={y1,y2,…,yu}(yj∈I*,1≤j≤u)为2-项集.如果X⊂Y并且每个项在TWU升序排序中都在X的项之后,则Y是X的扩展.例如,图1中{CAE}并非{CE}的扩展,而是{CA}的扩展.因为根据表2示出的滑动窗口SW1中各项的TWU,以TWU的升序排列的项的顺序为FBDCAE.在此,{A}排在{E}之前. Table 2 TWU Information of Items in SW1表2 SW1中项的TWU信息 本文提出一种名为BRU_table的双重散列表,该结构是在对当前窗口第1次事务扫描时被构建或更新的,包含了当前窗口的所有批次,并为每个批次给予一个唯一的编号,其值为该批次所包含的事务Tid和该事务对应的BRU,BRU初始值为每个事务的事务效用.随着窗口的滑动,批次更新的同时散列表的项也会随之更新.待新批次到来,在移除各项CH-List旧批次信息时同步移除其批次的BRU_table项. BRU_table作为临时存储结构,为新窗口的事务重组提供了必要信息.因为随着新批次的到来,项的TWU和顺序已经发生变化,根据属性6,剩余效用修剪策略将无法正确对新搜索空间进行剪枝.需要根据当前事务元组信息和TWU顺序重构前一窗口和新窗口的CH-List公共批次事务元组.从更新后TWU最小的项开始遍历公共批次中所有CH-List,并相应地更新RU值.在遍历时,使用BRU_table中存储的相关批次散列表及其初值来存储和计算具有相同Tid的RU值,并且每个散列项条目处的BRU值将减去该处当前RU值.不同于IncCHUI[23]的全局列表更新结构,本文提出的结构不需要对项的总顺序倒序遍历,且适用于滑动窗口机制.图2为一个BRU_table结构示意图,此时其存储的是第1个窗口2个批次的事务信息. Fig.2 BRU_table in SW1after the first scan图2 窗口SW1首次扫描后的BRU_table 各批次构成的FIFO队列效用信息由CH-List维护,该结构记录先前与当前窗口的项集有关效用信息.在提出的算法中,批次事务中的每个项(集合)都与一个CH-List列表相关联.项(集合)X的CH-List包括Utility-List以及一种名为HistorySet(X)的有序集合.X的Utility-List由当前窗口各批次的事务元组组成.X的Utility-List中的各个元组存储在以批次号(Bid)为键、批次元组为值的散列表中.每个元组代表重组事务Tr中X的效用信息,并具有3个字段:Tid,EU和RU.Tid存储包含项集的事务标识符,EU是项集的实际效用,RU是项集的剩余效用.当新批次的事务到达时,按这些事务构造的元组会被添加到队列的尾部.一旦队列的大小超过窗口大小,则将属于第1批次的元组从项的CH-List中移除.可以看出,在滑动窗口滑动过程中,其效用信息更新是以批次为单位的.CH-List相较于传统EU-List[20]数据结构的优点是它可以快速执行批次的插入和删除.例如,分别在图3(a)(b)中示出了滑动窗口SW1和SW2中项{A}的CH-List变化情况. Fig.3 CH-List{A} in different windows图3 不同窗口的项{A}的CH-List变化 Fig.4 CH-List{CA} in SW1图4 项集{CA}在SW1的CH-List 通过扫描滑动窗口2次来构造CH-List数据结构.在第1次扫描中,将计算项的TWU和事务效用.在第2次扫描期间,根据TWU的升序对每个事务中的项目进行排序,由上述过程产生重组事务.接着程序为每个项更新CH-List信息,由2个项组成的项集,其CH-List的Utility-List部分是通过将单个项的Utility-List相交而创建的.第1步是查找包含2个项的批次.例如SW1中,要分别从CH-List{C}和{A}构造项集{CA}的CH-List.{C}和{A}的CH-List共同批次为B1,B2.一旦确定了其共同出现的批次,就确定了包含这2个项的事务.项{C}和{A}分别出现在事务T1,T3,T4,T6中.图4中显示了项集{CA}的CH-List.构造k-项集的CH-List的过程与上述过程相似. 定义19.在项集X的CH-List中,其EU和RU值的总和分别表示为SumEUSWk(X)和SumRUSWk(X),它们是将当前窗口SWk下列表所含所有批次事务的EU,RU分别相加得到的. 属性6.如果SumEUSWk(X)+SumRUSWk(X) 证明.设项集Y为X的扩展,X⊂Y,TidSetSWk(Y)⊆TidSetSWk(X).令Y/X表示Y中在X之后的所有项的集合.根据定义2和定义16,存在: 且 因此, 证毕. 收到一个新批次Bnew后,算法会检查该窗口SWk是否为初次创建,若非创建的首个窗口,则更新前一个窗口SWk-1中项的CH-List,删除这些CH-List中最旧批次Bold存储的信息;同时清除BRU_table中关于最旧批次事务的相关值(算法1的行①~④).逐个遍历新批次的事务,对事务中的项进行扫描,检查它的CH-List是否为空.若为空,则算法创建其CH-List结构,并计算当前批次所在窗口SWk下各项的TWU.否则,为当前项更新该批次插入后的TWU.本文的算法逐批维护事务中项的TWU,以便在新批次到达并移除最旧的批次时可以迅速更新项的TWU.同时新批次的各事务效用会被添加到BRU_table散列表中(算法1的行⑤~). 若窗口批次数达到设定值,令SWk中所有项属于集合I.按对集合I中各项的CH-List排序(算法1的行~).接下来通过BRU_table及CH-List公共批次信息进行公共批次事务重组.在算法2中,按照项的TWU升序遍历各项在公共批次的所有事务,根据当前事务元组信息和各事务BRU重构事务元组,更新项的CH-List,同时更新各事务的BRU值(算法2的行①~⑦).以图1为例,SW1与SW2窗口公共批次B2中{C},{D}的CH-List和BRU_table在重构过程中变化分别如图5和图6所示. Fig.5 CommonBatches changes during revised CH-List图5 SW2公共批次重组过程中CH-List变化 Fig.6 BRU_table changes during revisedCH-List in SW2图6 SW2公共批次重组过程中BRU_table变化 紧接着返回算法1,对SWk中除公共批次之外的批次进行第2次扫描,以创建和更新CH-List中的元组信息.待I中所有项的CH-List创建完成,根据属性5筛选出所有高TWU的项组成集合I′(算法1的行~). 算法1.CHUI_DS算法. 输入:批次Bold,Bnew;窗口大小winSize;批次事务数number_of_batches;列表CH-List;窗口SWk;阈值minutil;项的集合I. 输出:数据流中所有CHUI. ① ifSWk不是首个滑动窗口then ② 更新前一窗口SWk-1中属于I的项的 CH-List; ③ 将最旧批次Bold从BRU_table中移除; ④ end if ⑤ for事务Tr∈Bnewdo ⑥ 构造记录(Tid,TU)插入BRU_table(Bnew); ⑦ foritem∈Trdo ⑧ ifitem的CH-List不存在 then ⑨ 创建CH-List,更新item的集合I; ⑩ 首次计算item的TWUSWk; 算法2.公共批次事务重组算法. 输入:列表CH-List、散列表BRU_table、窗口SWk; 输出:公共批次事务重组后的CH-List. ① forCL(i)∈CH-List组成的集合 do ② forCL(i)在窗口SWk-1和SWk公共批次中的全部元组do ③ 元组RU=BRU_table[Bid][Tid]-元组EU; ④BRU_table[Bid][Tid]=元组RU; ⑤ end for ⑥ end for ⑦ 返回CH-List. 接下来就可以开始窗口SWk的挖掘过程,调用算法CHUI_DS_Miner以使用有前途的项构成的集合I′生成CHUI.该过程具有5个输入参数:1)项集X;2)HistorySet(X);3)X的扩展(extendOfX);4)minutil;5)窗口SWk.对于该算法发现的每个闭合项集X,构造其CH-List来计算其效用,以确定其是否为CHUI.如果实际效用和剩余效用之和小于minutil,则将修剪搜索空间.CHUI_DS_Miner的伪代码如算法3所示: 算法3.CHUI_DS_Miner算法. 输入:项集X、集合HistorySet(X)、X的扩展集合extendOfX、阈值minutil、窗口SWk; 输出:窗口SWk中所有CHUI. ① for项a∈extendOfXdo ② 将a从extendOfX移除; ③Y←X∪a; ④ 初始化extendOfY={}; ⑤ 构造CH-List(Y); ⑥HistorySet(Y)=HistorySet(X); ⑦ ifSumEUSWk(Y)+SumRUSWk(Y)≥ minutilthen ⑧ ifSubsumedCheck(Y,HistorySet(Y))= false then ⑨ for项Z∈extendOfXdo ⑩ ifTidSetSWk(Y)⊆TidSetSWk(Z) then SumRUSWk(Y) History-Set(Y),extendOfY, minutil,SWk); 定义20.闭合项集的包含.如果Y⊂S并且SUPSWk(Y)=SUPSWk(S),则项集Y被包含在项集S中.例如SW1中,{C}被{ACE}闭合包含,因为{C}⊂{ACE}并且SUPSW1({C})=SUPSW1({ACE}). 属性7.在SWk中,给定2个项集X和S,如果X⊂S且SUPSWk(X)=SUPSWk(S),则closure(X)=closure(S). 属性8.在SWk中,给定1个项集X和1个项Ii∈I*(1≤i≤m),则TidSetSWk(X)⊆TidSetSWk(I*)和I*∈closure(X)互为充要条件. 根据定义20,如果存在1个包含Y的已挖掘的闭合高效用项集S,则可以得出结论:Y没有闭合,并且closure(S)=closure(Y).因此,可以安全地修剪项集Y并停止探索Y后续超集的搜索空间.否则,程序继续向下探索. 假设Y通过了闭合包含检测过程,接下来计算Y的闭包,并将Y更新后的CH-List结构作为其闭包的CH-List(算法3的行⑨~).其执行过程为:初始化extendOfY集合,对于extendOfX中的每个项Z,算法检查TidSetSWk(Z)中是否包含TidSetSWk(Y).由属性8可知Z是否包含在Y的闭包中.若包含,则在extendOfX中移除Z,并将Z添加到Y,更新Y的CH-List.处理完extendOfX中的所有项后,根据此时extendOfX的值,更新extendOfY,返回更新后已经闭合的Y和extendOfY. 与DCI_CLOSED[32]和IncCHUI[23]相比,本文算法依据属性6,通过添加剩余效用剪枝策略修剪潜在低效用的闭包候选对象(算法3的行),避免了构造低候选效用或非闭合项集的效用列表. 若Y的实际效用不小于minutil,则算法3输出Y为CHUI,因为Y满足条件:闭合项集、高效用项集.然后CHUI_DS_Miner算法调用自身以进一步递归探索搜索空间并找到作为Y后续超集的CHUI.递归过程完成后,将项a添加到HistorySet(X)中.待对所有项遍历完毕,得到该窗口SWk中所有CHUI. 在滑动窗口模型中,最后winSize-1个批次在2个连续的窗口之间保持相同.即在对新的窗口扫描前,上一窗口项其CH-List最后winSize-1批次的元组将得到保存.因为其为挖掘下一窗口闭合项集提供必要事务计数信息.同时,由于进入新滑动窗口,项的TWU被重新计算,CH-List也需要更新.因此,相比于EU-List,CH-List取消了每个项的PostSet属性,CHUI_DS中的全局extendOfX结构在实现PostSet原有功能的基础上,仅在项进行排序后初始1次,节约了内存空间. 接下来,本文通过一个例子来说明算法的工作原理.考虑图1中所示的数据库.令minutil=30,窗口大小为2.第1个窗口由批次B1和B2组成.每条事务中的项均按照TWU的升序排序.对于第1个滑动窗口,项的排序为FBDCAE.获取完整的滑动窗口后,本文的算法将构建单个项的CH-List,由于每个项的TWU全部大于30,因此将其全部加入extendOfX中. 依次向CHUI_DS_Miner传入∅,HistorySet(∅),extendOfX等参数,开始遍历extendOfX,并首先处理其中的第1个项{F}.同时将{F}从extendOfX集合中去除,而后∅和{F}进行组合得到{F},并构建其组合后的CH-List.因为X此时为∅,所以: HistorySet({F})=HistorySet(∅)=∅. 下一步对{F}进行包含检测,由于{F}是初始结点,不会出现被前项包含的情况.因此可通过集合extendOfX计算{F}的闭包.首先循环extendOfX中的各项,此时因为{F}的Tid集合不含于{B}所在的集合,于是跳过本项直接进入下一循环.否则,基于{F}的事务集合构造{FB}的效用列表,并将{B}从extendOfX中删除.待遍历完最后1个元素,返回的结果是{F},extendOfX={B,D,C,A,E}.因为USW1({F})=36,所以{F}为找到的第1个CHUI,支持计数为3.之后递归进行搜索,此时的X={F},其继续和{B}联接,由于SumEUSW1({FB})+SumRUSW1({FB})=32+22=54>36,因此可以进行闭包计算,此时Y={FB}.直到递归完{F,B,D,C}下的所有搜索空间,HistorySet({FBD})={C},紧接着遍历{F,B,D}的其余搜索扩展{A,E},由于2次执行SubsumedCheck均返回false,所以本次递归停止,开始回溯.此时HistorySet({FB})={D}.以同样的方法,算法完成对剩余所有搜索空间的搜索,最终完成对第1个滑动窗口的闭合高效用项集挖掘. 在下一批次B3到达时,算法1构造滑动窗口SW2.窗口SW2中的项目TWU如表3所示.算法从第2个窗口中继续运行以挖掘CHUI,当没有新传入的批处理数据时算法终止. Table 3 TWU Information of Items in SW2表3 SW2中项的TWU信息 本节提供了广泛的实验以评估算法的效率,包括其在3种情况下的性能:1)最小效用阈值;2)窗口大小和批次数;3)数据集的大小(可伸缩性测试).由于CHUI _DS是第1种用于数据流环境挖掘CHUI的算法,因此,针对最新的CHUI挖掘算法,评估其性能的可靠方法是将其与静态或增量数据库中现有的算法进行比较.对于情况1(变化最小效用阈值角度)和情况3(变化数据集大小的角度),本文的算法CHUI _DS以单窗口批处理方式运行,对比算法包括CHUI-Miner[20],EFIM-Closed[21],CLS-Miner[22],IncCHUI[23].CHUI-Miner,IncCHUI采用效用列表结构,IncCHUI是目前为止最先进的增量闭合高效用挖掘算法,具有与算法CHUI _DS类似的搜索技术.而EFIM-Closed利用数据库投影和事务合并技术,是目前对静态数据挖掘闭合高效用项集最高效的算法之一.情况2中,实验主要通过控制窗口和批次大小对算法的影响来验证算法性能,对比算法是去掉闭包计算过程剪枝策略的CHUI_DS,称为CHUI_DS(no_sup).表4列出了本文用于实验的数据集,包括稀疏和密集数据集.其中Connect数据集是真实的数据集,但具有合成效用值,内部效用值是通过在[1,10]中均匀分布生成的,其余数据集为真实效用值. Table 4 Details of the Datasets表4 实验数据集 本节在每个数据集上运行所有比较的算法,同时逐渐增大最小效用阈值,直到观察到明显的对比结果为止.执行时间包括读取输入数据、发现项集以及将结果写入输出文件的总时间. Fig.7 Runtime comparison when varying utility threshold图7 不同效用阈值时的运行时间比较 在图7中,所有对比算法的运行时间都随着minutil的增加而逐渐降低至某个较低水平,因为算法的运行时间与产生的中间项集数量成正比,当阈值越大时,产生的中间项集越少,其运行时间就越短.在这个过程中,不同算法使用的数据库扫描方式、闭合项集搜索策略以及剪枝策略都不尽相同,造成下降速率也随之不同.在Connect数据集上,本文提出的算法运行时间大幅小于除EFIM-Closed之外的所有算法.尽管minutil较大时,EFIM-Closed比其余算法快;但当minutil较小时,EFIM-Closed需要增加大量执行时间,消耗的时间最大.这是因为Connect数据集平均事务长度在实验的所有数据集中最长,而EFIM-Closed需递归构建子投影数据库,这个过程依靠多次查找每条投影事务数组以寻找待扩展投影项索引,阈值低时的侯选待投影项数量巨大,近而导致EFIM-Closed在该数据集上表现差异较大.因此本文提出的算法在该数据集不同阈值下平均运行时间最低,总体表现优异.对于其他数据集,本文提出的算法比IncCHUI,EFIM-Closed都要略快,并且和CHUI-Miner拉开了较大差距.特别是在Connect,Mushroom,Chainstore数据集上,当阈值设置较低时运行时间大约比IncCHUI,EFIM-Closed缩短1/2.此外,当在Foodmart,Mushroom数据集上降低minutil时,本文算法的运行时间几乎相同.同时可以看到CHUI-Miner在绝大部分数据集上具有最大的时间消耗.原因可以解释如下. 尽管CHUI-Miner,CLS-Miner,IncCHUI和本文的算法采用相似的效用列表结构,但是CHUI-Miner和CLS-Miner都使用传统的效用列表,需要2次扫描数据库以构建效用列表,且在闭包计算等过程缺乏修剪策略.这也适用于EFIM-Closed,即使它采用了不同的技术来降低数据库扫描的成本.IncCHUI其闭包计算过程并没有使用适用于非增量环境的修剪策略,因此在阈值较低时慢于本文提出的算法. 在滑动窗口模型中,算法使用2个参数:1)窗口中的批次数量;2)批次中的事务数量.为了分析它们的影响,本节使用密集的数据集“Accidents”和稀疏的数据集“Chainstore”在各种参数下进行实验.其中Accidents的实验阈值设定为1.5×107,Chainstore的实验阈值为9.5×107.由于比较的算法是基于窗口的,因此其挖掘性能通常取决于窗口大小和批次大小.首先,比较窗口中含不同批次时的总运行时间,即固定Accidents每个批次的事务数为3×104,Chainstore每个批次的事务数为1×105.2个数据集的窗口大小参数设置,以及实验结果如图8所示: Fig.8 Accumulated runtime comparison when varying window sizes图8 不同窗口大小下运行时间对比 图8表明,CHUI_DS(no_sup)在2个数据集中表现都要慢于CHUI_DS.特别是在Accidents这种密集程度较大的数据集上,表现差距较大.原因在于本文是利用改进的闭包计算和递归搜索进行项集的闭合扩展,而密集数据集相比于稀疏数据集需要更多次深度搜索.若无有效的剪枝策略,在这个过程会产生大量候选项集,导致程序计算的成本大幅增加.与CHUI_DS(no_sup)相比,CHUI_DS在CHUI-Miner,IncCHUI的基础上对闭包挖掘过程额外增加了剪枝策略,同时利用提出的高效列表重组方法,使该剪枝策略能适用于任意滑动窗口,以此保证每个滑动窗口处理速度都得到提升.尽管公共批次列表的重组会产生一定时间消耗,但该过程并不需要重新扫描数据集,相较于剪枝掉的时空代价对算法效果影响有限.尤其是在阈值和数据集大小一定的情况下,加大窗口内批次数意味着事务数的增加,密集数据集下的候选项集将成数倍增大,对算法运行时间影响较大.由于Chainstore数据集的稀疏性,列表可复用率低,新增的中间候选项集数相对较少,由此其候选项集数量受窗口增大的影响较轻.尽管前期算法运行时间略微增加,但随着窗口的扩大,算法对整个数据集窗口滑动和垂直数据结构更新的次数明显减少,因此2种算法运行时间后期均出现下降. Fig.9 Accumulated runtime comparison when varying batch sizes图9 批次内含不同事务数下运行时间对比 考虑算法固定窗口内的批次数为2,比较批次中事务数不同时的总运行时间,2个数据集的实验参数设置及结果分别如图9(a)(b)所示.实验逐渐增加每个批次中的事务数,运行时间的变化趋势和数据集的稀疏类型关系较大,具体表现为Accidents数据集运行时间逐渐变长,而Chainstore数据集运行时间变短.原因在于Accidents这样的密集型数据集,其往往会生成大量长度较长的高效用项集.和图8实验部分给出的原因相似,对于Chainstore稀疏数据集而言,因略微增大批次事务数而新增的中间候选项集数较小,批次中事务数越多从一定程度上减少滑动窗口的创建次数和挖掘算法的执行次数,因此算法运行时间稳步下降.实验同时证明,与CHUI_DS(no_sup)相比,CHUI_DS具有更大的可扩展性,适用于大型窗口. 本节选取表4中的Mushroom,Retail数据集评估算法的可扩展性,以验证本文算法的运行时间和内存消耗没有呈指数增长.实验是根据总运行时间和内存进行的,采用4.1节实验中使用的最低minutil来执行相关工作中的算法.需要注意的是,IncCHUI在本实验部分以增量方式运行,即使用数据集中20%的事务作为原始数据集,然后分别对Mushroom,Retail数据集按5%,10%的插入率添加到原始数据集. Fig.10 Scalability test of runtime图10 运行时间可扩展性测试 图10显示了运行时间评估的结果.IncCHUI的运行时间是处理每个递增部分的时间,其余算法的运行时间是累积的执行时间.本文的算法使用单窗口运行,因为其余算法均以批处理模式运行在静态数据集中.可以看到,当使用的数据集事务变多时,5种算法都需要更多的执行时间,其中在密集数据集Mushroom中CHUI_DS具有最佳的可伸缩性,在稀疏数据集Retail中CHUI_DS和IncCHUI性能均接近最优.CHUI_DS运行速度最快的原因是,与CLS-Miner和EFIM-Closed相比,CHUI-Miner仅采用了简单的TWU高估策略.尽管IncCHUI增加了相关修剪策略,但其以增量方式插入原始数据库,每次新数据到来都需要对项逆TWU顺序遍历,并依此进行先前全部效用列表事务元组的更新,且其需要判断闭合项集是否存在于已发掘的CHT表中,特别是当数据密集时时间开销会增加较快. Fig.11 Scalability test of memory图11 内存可扩展性测试 在内存使用方面,图11中实验结果表明:CHUI_DS在Mushroom数据集上的内存消耗比绝大部分算法都要低.在Retail数据集上,CHUI_DS随着其事务数量的变化内存总体呈增加趋势,相较于Mushroom数据集,算法产生更多的中间项集,内存占用普遍大于Mushroom数据集.但由于Retail数据集的高稀疏性,随着事务的阶段性增加,产生的中间项集数量和高TWU项在该阈值条件下并非一直大幅增多.在此基础上,非闭合的项集冗余比例在部分阶段略微增大,导致内存消耗呈阶段性增长.总体来说,CHUI_DS在各数据集整个挖掘过程的最大内存结果合理,运行时间和内存消耗均没有呈指数增长.通常,对于所有算法,内存消耗的趋势会根据所使用的数据集、算法采用的结构以及在挖掘过程中生成的候选总数而变化很大.例如,Retail是一个稀疏的数据集.在此数据集上,CLS-Miner消耗更多的内存,因为它需要存储其修剪策略的结构,例如项的覆盖范围和估计的效用共现结构.但是此数据集上CLS-Miner的运行时间非常低.在密集数据集Mushroom上,由于其覆盖修剪策略的有效性,CLS-Miner的内存消耗较低,IncCHUI在此数据集上的总体内存消耗几乎最少,这是因为其在此部分的实验以增量方式运行,只需要扫描数据库1次以构建全局列表,采用候选项集构建的增量修剪策略和高效用闭合项集更新机制来节约内存占用,而在Retail数据集上又高于CHUI_DS. 综合来看,本文提出的算法对于不同类型数据集均有较强适应能力,总体性能良好.特别是在不同阈值、不同数据集大小等条件下的时间性能要优于先前提出的所有闭合高效用项集挖掘算法,内存占用相对其他算法处于较低水平.所提出的算法不仅对滑动窗口大小和批次事务数量具有良好的可伸缩性,而且几乎在每种情况下都保持较低的时间消耗.这些结果验证了该算法在各种现实世界数据流环境中的挖掘效率.因此,所提出的算法可以作为基础部分应用于专家和智能系统,通过滑动窗口参数设置以及对现实世界数据库特性的考虑,帮助用户更轻松地分析数据流并从中获取有意义的信息. 为了应对数据流的动态特性带来的挑战,本文提出了一种称为CHUI_DS的新算法,其可以有效地挖掘和维护数据流中闭合的高效用项集CHUI,同时CHUI_DS也是第1种基于滑动窗口模型的数据流闭合高效用项集挖掘算法.首先,本文提出了一种新型效用列表结构,用于将数据流关键信息存储在项集中.此列表结构的一个重要方面是它能快速准确构建和更新数据流中的大量最新信息,适用于对数据流进行闭合高效用项集的挖掘任务.其次,本文基于该效用列表结构,提出数据流上无候选者产生的闭合高效用项集挖掘算法.第三,为了提高效率,本文对闭合项集挖掘过程进行改进,使用一个更加紧凑的效用剪枝策略.为了评估提出的算法,本文对现实和合成数据集进行了广泛的实验,并将其与现有算法进行了比较,该评估证实了本文算法的效率和可行性.3 CHUI_DS算法

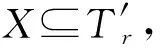

3.1 数据结构BRU_table和公共批次事务重组

3.2 CH-List数据结构
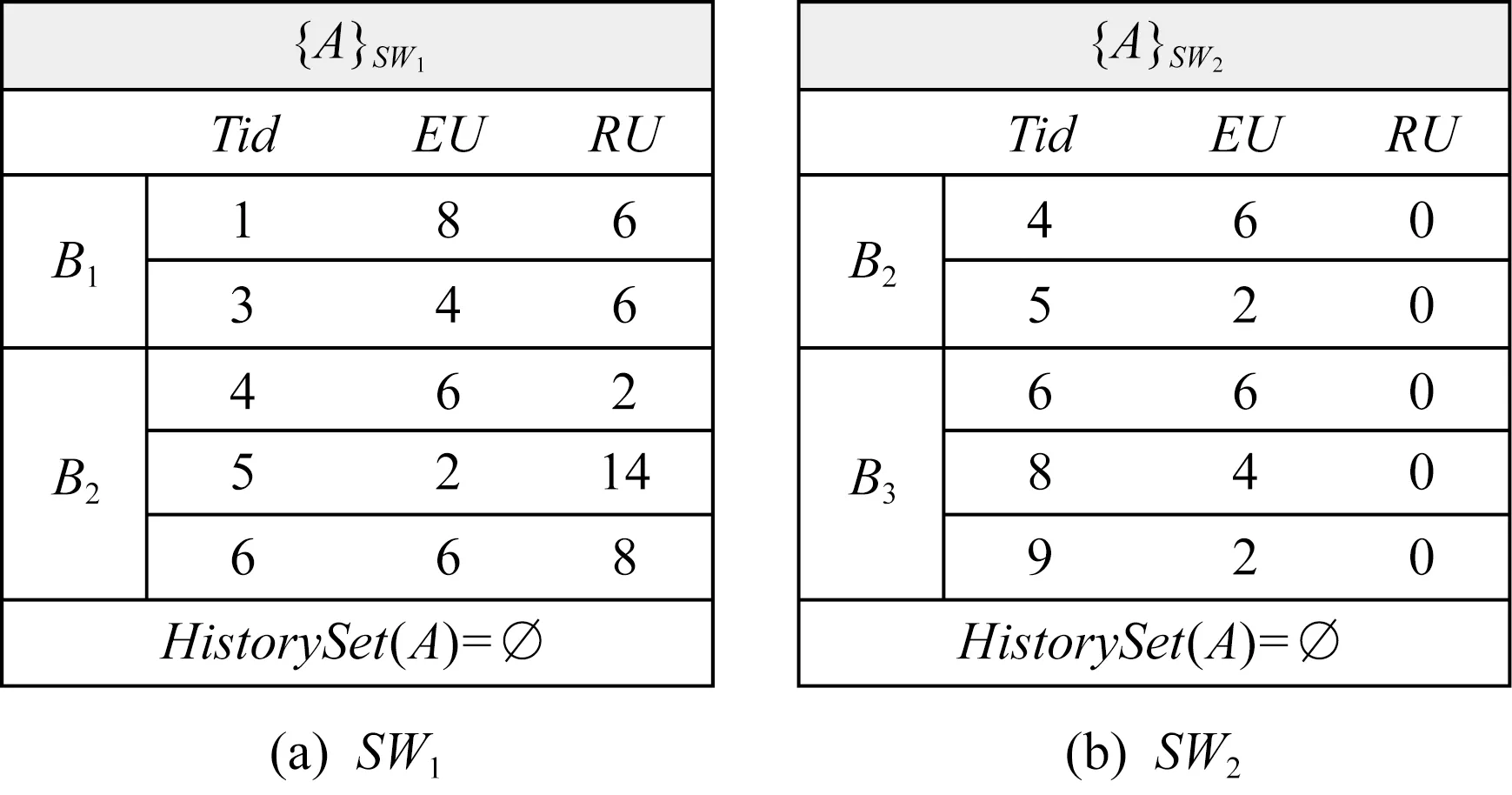
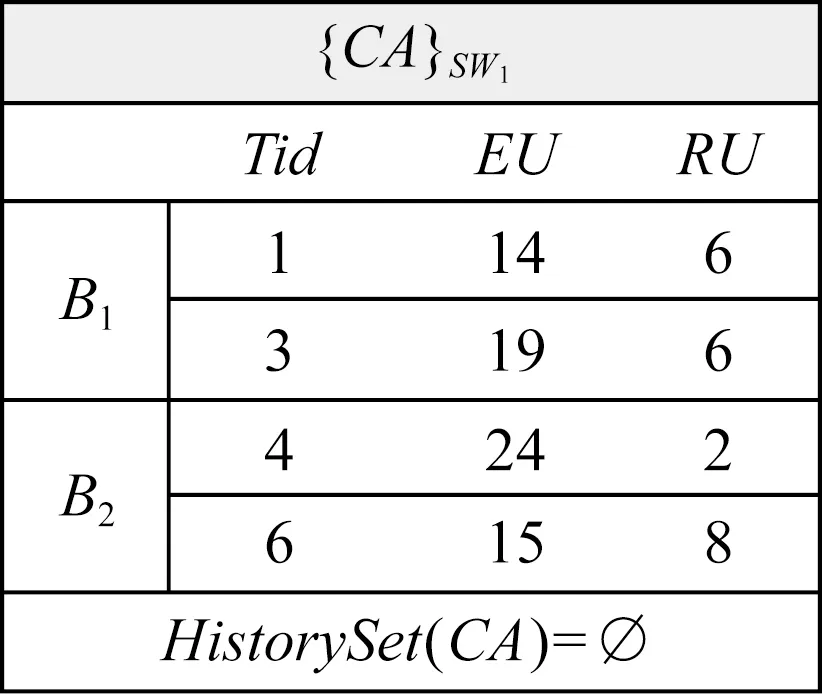

3.3 CHUI_DS


SumEUSW1({F})+SumRUSW1({F})=
36+57=93>30.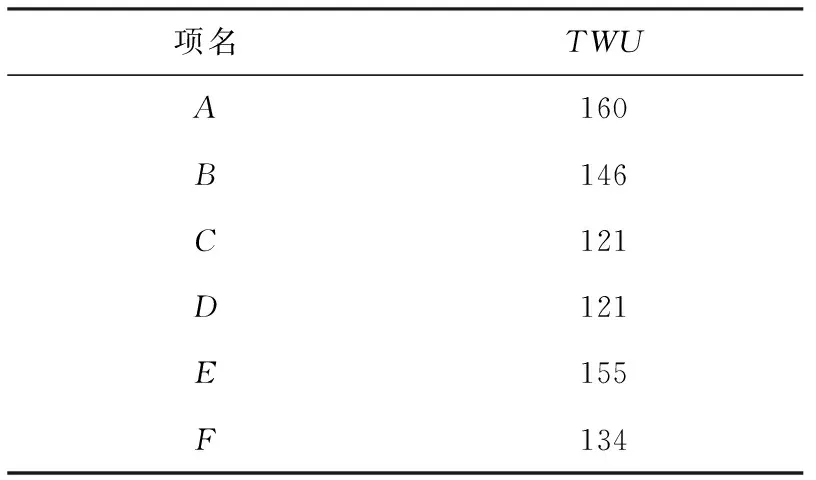
4 实验与结果

4.1 最小效用阈值的影响
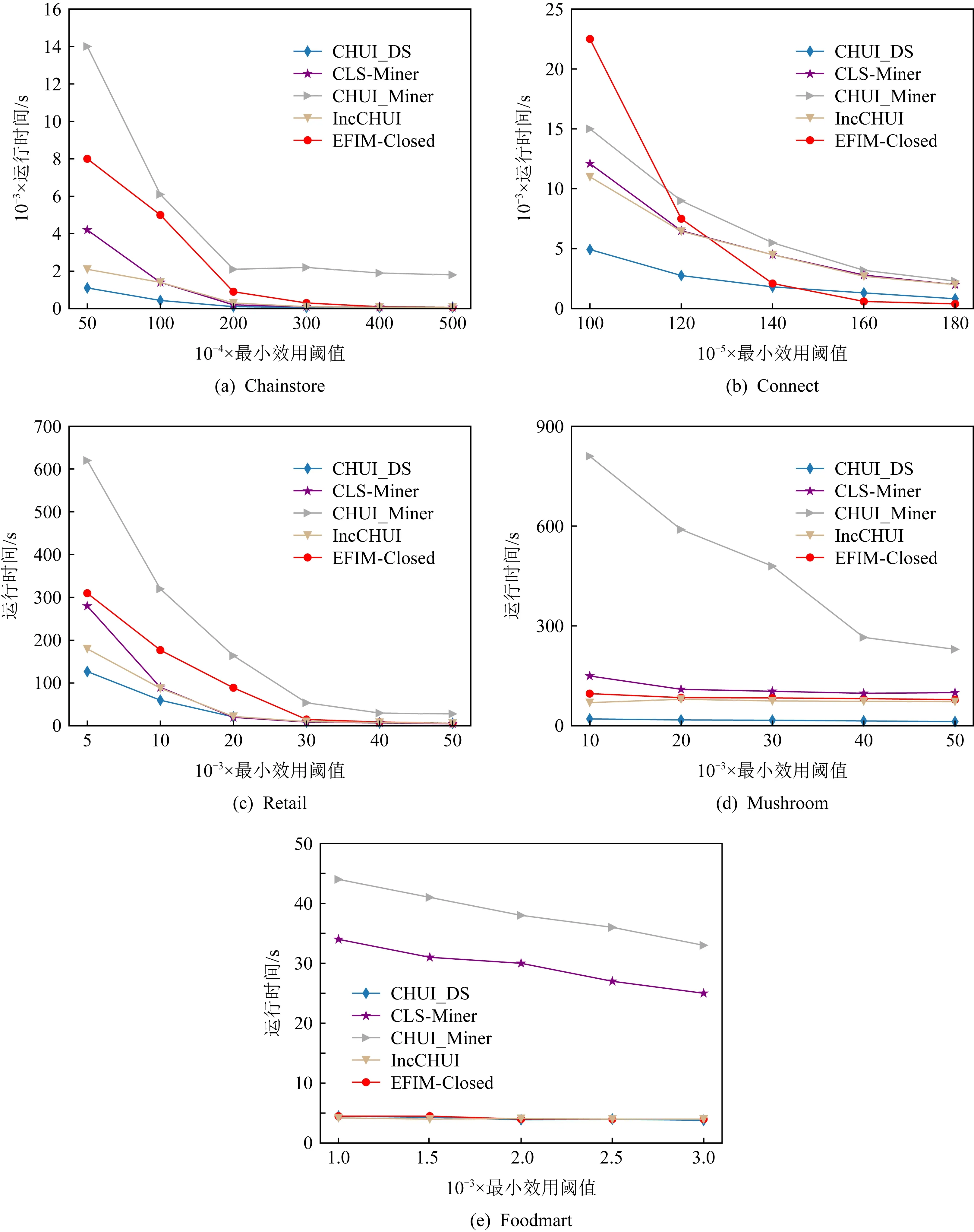
4.2 不同窗口和批次大小的效率测试
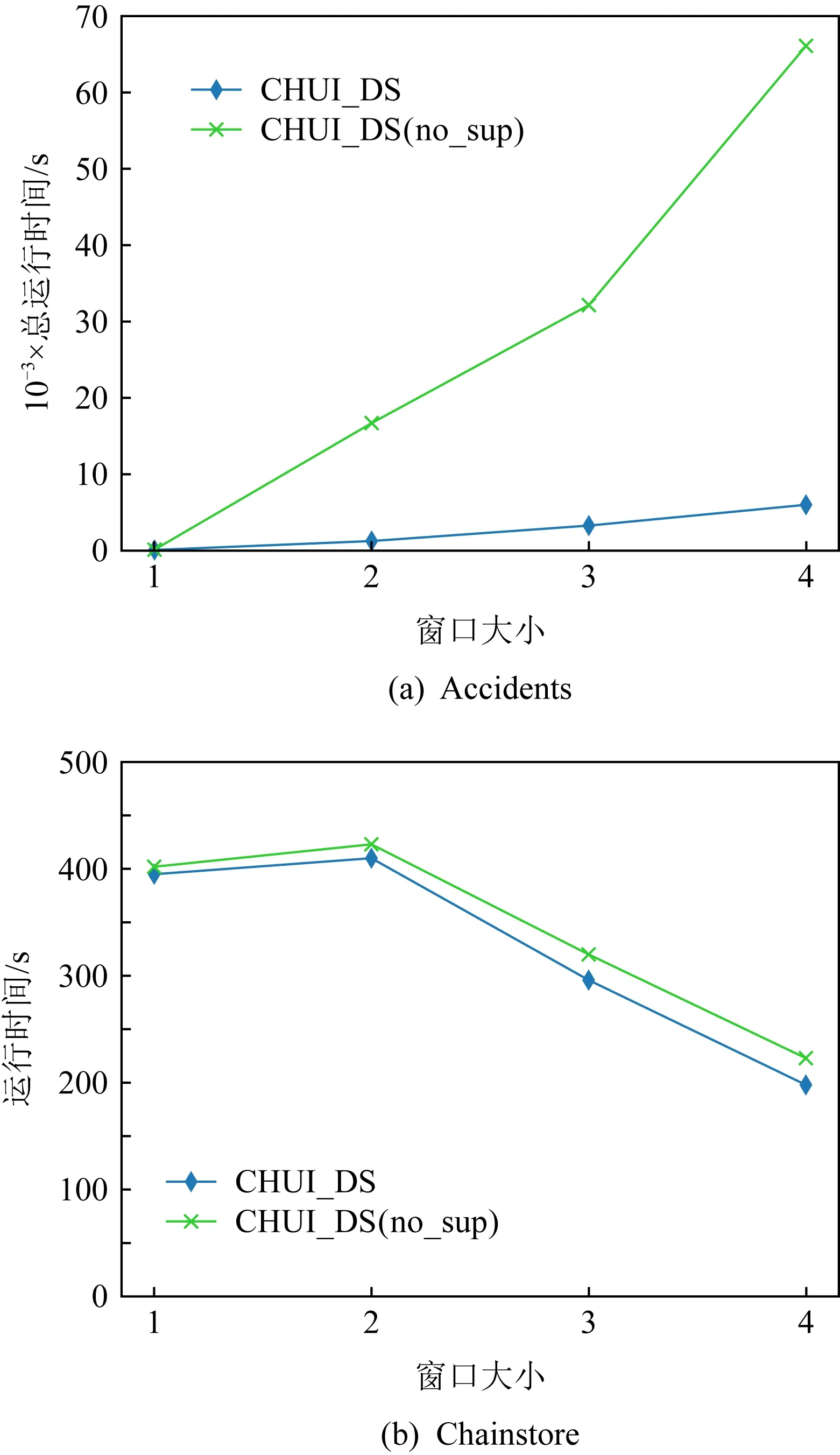
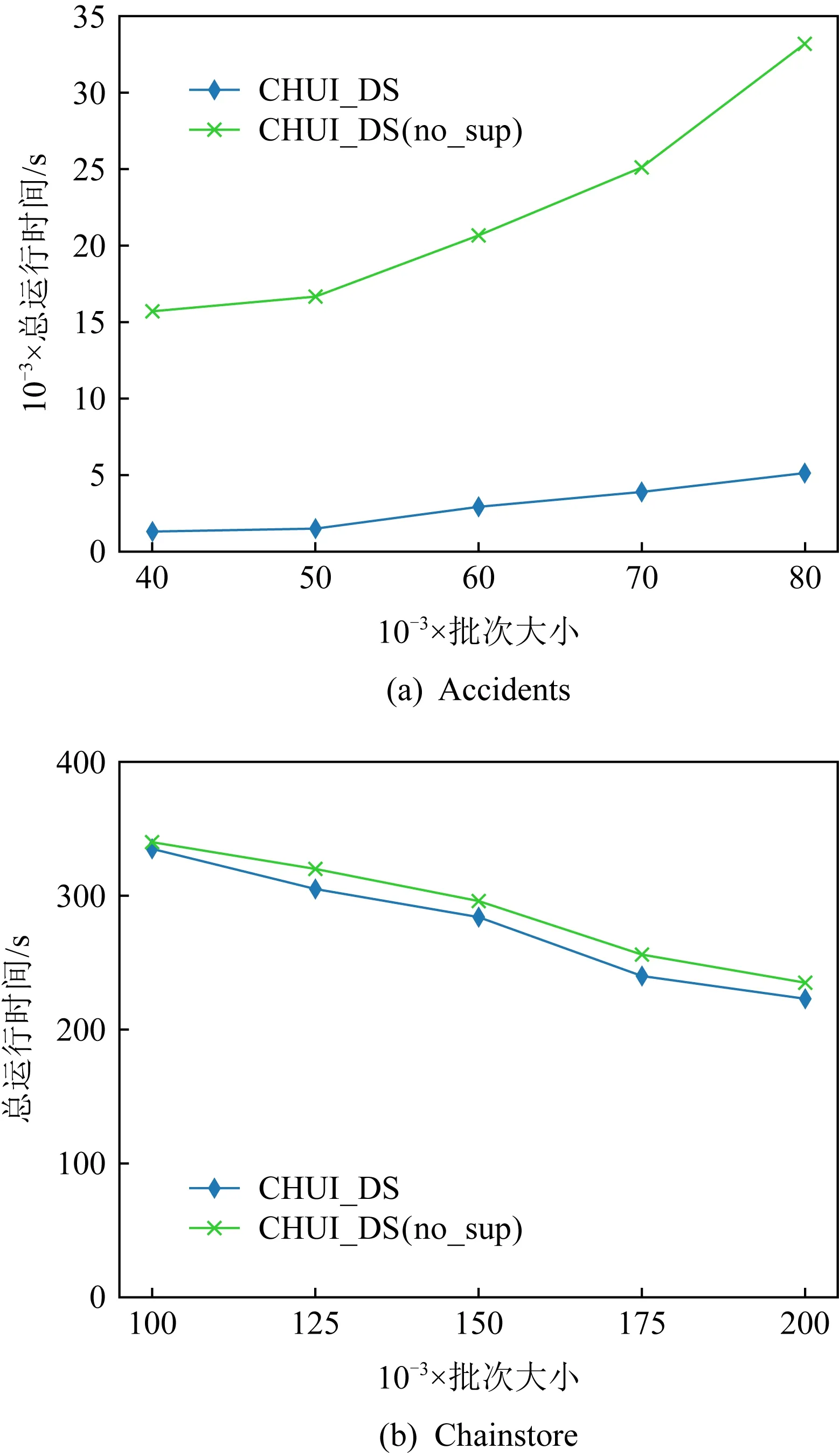
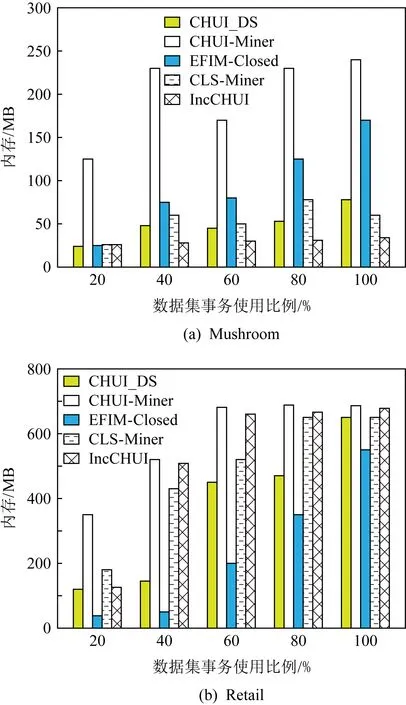
4.3 可扩展性测试

5 总 结
