基于改进迭代最近点算法的接骨板贴合性快捷计算方法

朱新成，何坤金，3*，倪 娜，郝 博

（1.河海大学物联网工程学院，江苏常州 213022；2.常州市图形图像与骨科植入物数字化技术重点实验室，江苏常州 213022；3.疏浚技术教育部工程研究中心，江苏常州 213022）

0 引言

随着我国人口老龄化的加剧和生活中各类交通事故的频发，骨折患者不断增加。目前，外科手术中最常见的骨科植入物有接骨板、髓内钉、钢针等，其中接骨板的设计是植入物设计的核心［1］。接骨板作为临床上应用最为普遍的内植入物之一，其作用是保持骨折端的复位状态，提供良好的稳定性［2］，因此接骨板在手术中贴合位置的准确性对患者的术后恢复起着关键作用［3］。由于术前医生只能大致判断接骨板的贴合位置，并在术中需要对接骨板位置进行多次调整，这无疑增加了手术的难度，延长了手术的时间。因此，提前计算出接骨板的最佳贴合位置能够指导医生更好地进行术前规划，这对于计算机辅助医生进行高效诊疗有着重要的意义。

近年来，数字骨科［4］不断发展，成为推动骨科临床发展的重要动力。Schmutz 等［5］通过计算机在全虚拟环境下对胫骨远端内侧接骨板的贴合性进行评估，并提出了在不同部位接骨板到骨表面之间间隙的最低要求；吴旭华等［6］利用接骨板与骨骼表面之间间隙的体积和接骨板内曲面面积之间的关系来对不同接骨板的贴合性进行比较；Harith等［7］提出使用多个贴合指标以及接骨板与骨面的最大距离衡量临床治疗结果，并开发了一种用于自动钢板定位和贴合性评估的软件工具，以达到植入物设计验证和优化的目的；Malekani 等［8］分析了316L和Ti-6Al-4V不锈钢接骨板并进行压力性能测试，为手术中贴合性不佳且需要手动弯曲调整的接骨板提供了一个指导性标准。贴合性良好的接骨板可以更好地帮助医生借助接骨板对骨折进行复位，减少接骨板对软组织的影响［9］。上述研究提出了接骨板贴合指标，衡量了部分厂家的接骨板贴合性，但并未提供有效的方式指导医生确定接骨板贴合的最佳位置。针对接骨板的研究有了一定的成果［10-12］，提出了个性化和系列化设计，为未来接骨板的发展趋势提供了新思路。由于技术水平和成本投入的限制，目前国内接骨板生产厂家仍是批量生产，这就使得即使接骨板的型号分得足够细，医生根据经验选取完合适的接骨板在手术中仍然需要多次比对找到与骨骼表面贴合最佳的位置，至今针对接骨板贴合性的计算方法研究较少。针对点云配准技术，Besl 等［13］提出了迭代最近点（Iterative Closest Point，ICP）算法，由于操作简单以及良好的配准效果得到了广泛的应用，但是ICP 算法对于点云的初始位置要求很高且配准效率低；Mitra 等［14］提出了一种基于二次距离框架的配准算法，同时利用点与点和点与面之间的距离来达到较好的配准效果，解决了两组点云初始距离远的问题，但是该算法需要计算每个点的曲率，导致计算量大，配准时间长；王欣等［15］提取点云模型边界的特征点，在初始配准的基础上，运用改进的ICP 算法进行精确配准，虽然算法效率提高，但是精确度不高；陈学伟等［16］基于采样一致性初始配准（SAmple Consensus Initial Aligment，SAC-IA）算法进行初始配准，再利用改进的ICP 算法精确配准，达到了较好的配准效果，但是配准时间较长；Liu 等［17］将K 均值聚类算法与改进权值比的ICP算法相结合，较传统的ICP算法虽然降低了配准时间，但配准效果不佳。。

由于胫骨周围的肌肉组织较少，骨头迎面区域在受到旋转用力或直接暴力时更容易发生骨折，因此，本文针对上述问题，以胫骨为例进行研究，在对断骨复位的研究成果［18］基础上，提出了一种基于改进ICP 算法的接骨板贴合性快捷计算方法。首先，选取胫骨表面的贴合区域，提取接骨板内曲面点云；然后，对两组点云平滑、采样处理，利用点云之间的特征关系初始配准；最后，提取接骨板特征关键点，采用K-维树（KDimensional Tree，KD-Tree）搜索邻近点对接骨板点云模型和胫骨区域点云模型执行ICP精确配准。

1 接骨板贴合性快捷计算的方法

为了指导医生能快捷有效地在断骨上确定接骨板最佳贴合位置，本文提出了一种基于改进ICP 算法的接骨板贴合性快捷计算方法，并以胫骨为例进行实验，算法流程如图1所示。

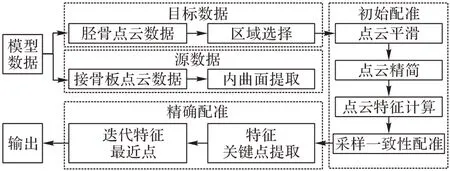
图1 本文方法流程Fig.1 Flowchart of the proposed method

根据设计流程，基于改进ICP 算法的接骨板贴合性快捷计算方法的主要步骤如下：

1）由医生指导通过鼠标框选出贴合区域，再计算接骨板点云的法向量，利用内、外曲面法向量之间夹角大于90°的特征提取内曲面点云。

2）对两组点云模型平滑处理去除噪点，再对两组点云模型格点采样以简化模型，利用点云之间的特征关系进行初始配准。

3）提取接骨板内曲面点云模型的边界及内部的特征关键点，采用KD-Tree 搜索邻近点对接骨板点云模型和胫骨区域点云模型执行ICP精确配准。

2 数据预处理

本文通过接骨板内曲面与胫骨表面距离来衡量接骨板贴合性，分别对复位后的胫骨和接骨板模型进行预处理，其中包括医生指导在胫骨表面选取贴合区域和利用接骨板表面法向量之间的夹角对接骨板内曲面提取。

2.1 胫骨表面区域选取

由于外科手术前医生只能通过断骨CT 图像大致确定接骨板的贴合位置，根据文献［18-19］已有的断骨复位方法，对复位后的胫骨与接骨板进行匹配，医生可以在术前规划时以交互的方式在胫骨表面选取大致的贴合区域，选取的区域如图2（a）所示。

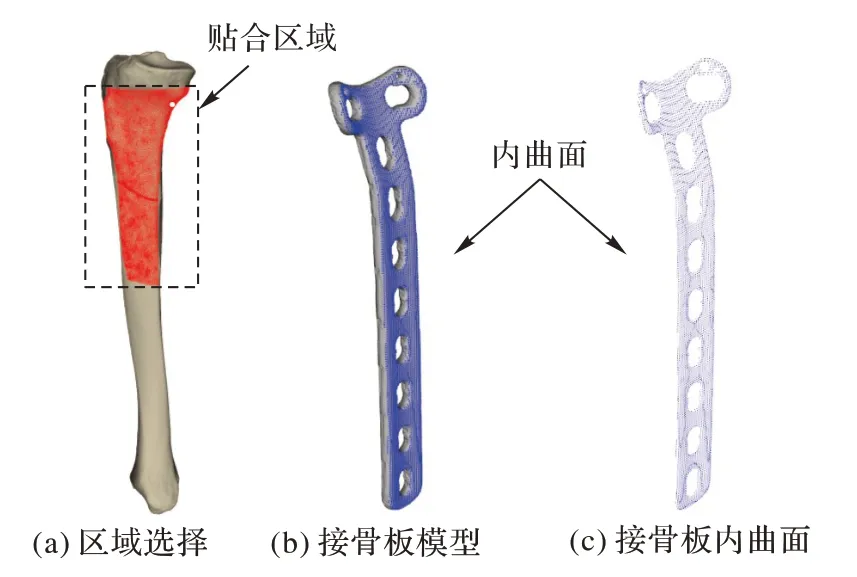
图2 胫骨和接骨板模型Fig.2 Model of tibia and orthopedic plate

2.2 接骨板内曲面提取

接骨板模型由生产厂家扫描真实接骨板得到，由内曲面、外曲面和侧面组成，为了提高接骨板与胫骨表面匹配度，接骨板在胫骨上的贴合性用接骨板内曲面与胫骨表面之间的距离衡量，因此，需对接骨板点云模型的内曲面进行提取。根据接骨板内、外曲面和侧面中包含点的法向量差异较大的特点，可利用点的法向量之间的夹角来获取接骨板内曲面，算法流程如下：

1）接骨板内曲面任意一点p0，计算出该点的法向量V0；

2）计算接骨板点云模型点(p1，p2，…，pn)的法向量(V1，V2，…，Vn)与点p0的法向量V0的夹角(a1，a2，…，an)；

3）若点pi的法向量Vi与V0的夹角ai小于阈值T，则将点pi记为接骨板内曲面的点。

接骨板模型如图2（b）所示，提取出的接骨板内曲面点云如图2（c）所示。

2.3 点云平滑

在对接骨板点云模型进行扫描时，可能出现扫描仪光线对过于弯曲的表面无法完全覆盖的情况，因此点云模型通常会出现点云不平滑甚至是空洞的状况。为了能够更加准确地表现点云特征，提高点云法线的准确性，采用移动最小二乘法（Moving Least Squares，MLS）［20］对周围数据点进行高阶多项式插值来平滑接骨板内曲面和胫骨选取区域点云模型。

在点云模型的一个局域子域U的拟合函数可以表示为：

式中：a(x)={a1(x)，a2(x)，…，an(x)}是坐标x的函数，为待求系数；p(x)={p1(x)，p2(x)，…，pn(x)}是一个阶完备的多项式，通常表示为[1，u，v，u2，v2，uv]T。

加权离散L2范式［21］为：

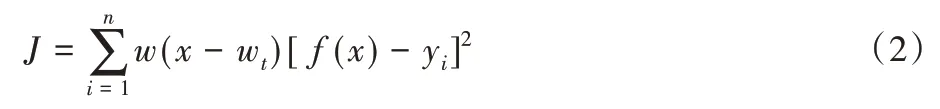
式中；n表示影响区域节点的数目，f（x）表示拟合函数，yi是x=xi处的节点值，w(x-xi)是节点xi的权函数。为实现点云平滑处理，权函数通常选择立方样条权函数：

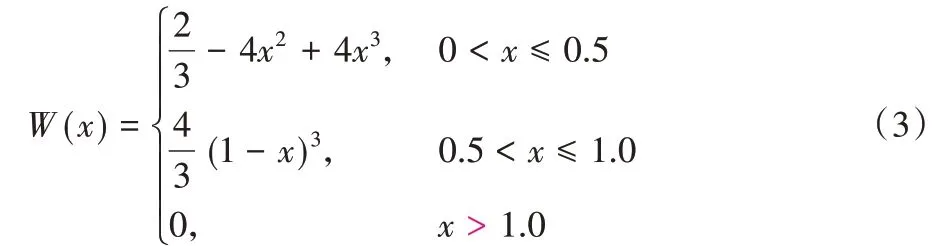
式中：x=；hi为第i个节点的权函数支持域的值；β为引入的影响系数范围，通常取1.2～2.5。

2.4 模型精简

为了降低计算量，节约计算时间，在保证接骨板贴合性不降低的前提下需要对两组点云模型进行精简。目前常见的点云精简方法是对点云模型进行采样，采样方法有均匀采样、几何采样、随机采样、格点采样等。为了保证精简后模型配准效果的有效性，采样点需要满足分布均匀且能较好地体现几何特征的条件，因此对接骨板内曲面点云模型分别进行均匀采样和格点采样，采样对比结果如图3所示。

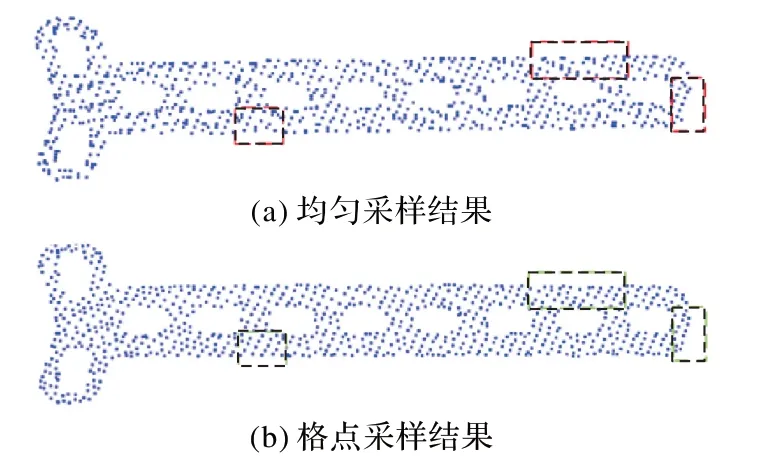
图3 采样结果对比Fig.3 Comparison of sampling results

接骨板内曲面点云个数为6 058，精简后的个数为833，均匀采样和格点采样所耗费的时间分别为0.108 s 和0.049 s；从图3 中可以看出，接骨板内曲面模型经过格点采样后的点云分布较均匀采样后的点云分布更为均匀且几何特征表现得更加明显。在本文实验中，格点采样的效率更高且采样结果更加符合本文实验的要求，所以本文采用格点采样的方法来精简点云模型。

计算点云模型各个顶点在x、y、z三个坐标轴上投影的最小值（lx，ly，lz）和最大值（mx，my，mz），过（lx，ly，lz）和（mx，my，mz）点，分别沿着x、y、z三个坐标轴方向构建一个长方体包围盒，以一定的间距R分别沿着x、y、z三个方向对最小包围盒进行等间距划分，最小包围盒内包含了若干个边长为R的小方格，每个小方格内有若干个点，取距离小方格中心最近的点即为采样点。由于胫骨点云模型相较于接骨板内曲面点云模型点云更加密集，几何特征也更加丰富，为了在精简模型的同时能够尽可能多地保留几何特征，对胫骨选取区域精简的采样半径R1应小于对接骨板内曲面精简的采样半径R2，胫骨选取区域和接骨板内曲面模型的精简结果分别如图4（a）、图4（b）所示。

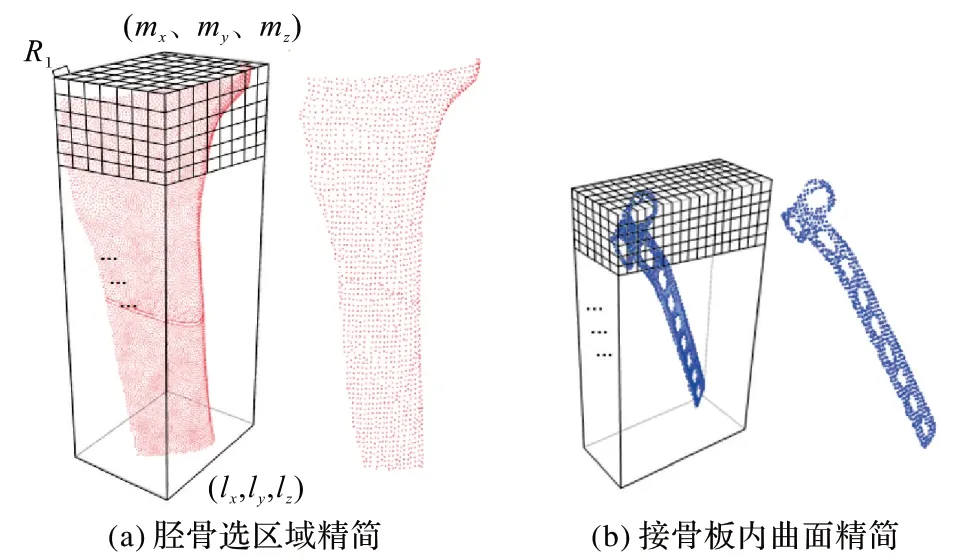
图4 点云模型精简结果Fig.4 Simplification results of point cloud model

3 接骨板贴合性计算

接骨板最佳贴合位置的寻找主要通过接骨板内曲面点云模型和胫骨选取区域点云模型配准来实现，为了实现高精度、高效率的配准，本文将改进的配准算法分为初始配准和精确配准，根据两组点云模型的特征采用SAC-IA 算法配准，能够避免精确配准时陷入局部最优的情况；提取接骨板内曲面特征关键点，采用KD-tree 搜索邻近点对两组点云模型执行ICP配准。

3.1 接骨板初始配准

本文初始配准利用了接骨板内曲面和胫骨选取区域点云模型之间点云的特征，首先分别计算两组点云的特征直方图（Fast Point Feature Histogram，FPFH）；然后使用SAC-IA 算法［22］对接骨板内曲面和胫骨选取区域的点云模型进行初始配准，初始配准算法流程如下：

1）在接骨板内曲面点云模型中选取n个点作为采样点，为了满足每个采样点FPFH 特征之间的差异性，采样点之间的距离应满足大于阈值dmin。

2）以点云模型中任意一点pi为圆心，计算半径为r范围内点云的特征直方图，然后在胫骨选取区域点云模型中搜索与接骨板内曲面点云模型中采样点FPFH 特征相似的点，将该点作为接骨板内曲面点云模型在胫骨选取区域内对应的点。

3）计算接骨板内曲面点云模型和其在胫骨选取区域对应的点云模型之间的刚体变换矩阵，惩罚函数表示为Es，使用Huber函数来衡量配准误差，ei表示每对点之间的误差，te为定义的误差范围。

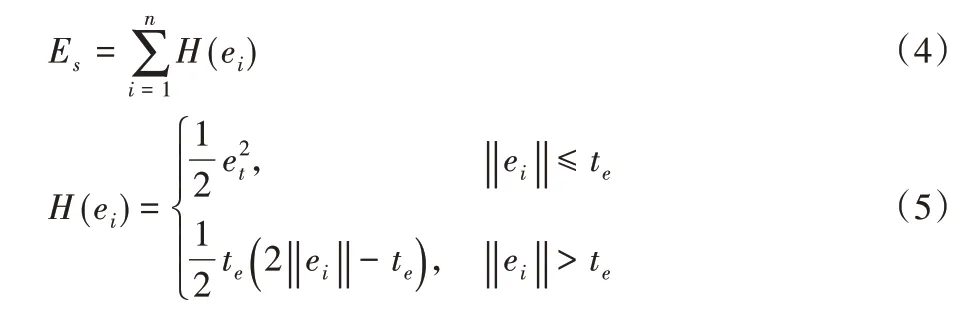
重复上述三个步骤，对点云模型内所有的点进行计算，当误差取最小时获得接骨板内曲面点云模型和其在胫骨选取区域对应的点云模型之间的变换矩阵即为最优变换矩阵，胫骨选取区域点云模型与接骨板内曲面点云模型初始位置如图5（a）所示，经过初始配准后的位置如图5（b）所示。

图5 初始配准结果Fig.5 Initial registration results

3.2 接骨板精确配准

初始配准是将距离较远且在不同坐标系下的两组点云模型配对到同一坐标系下，并为精确配准提供较好的初始位置。精确配准采用改进的迭代最近点（ICP）算法，在空间点云搜索上利用KD-Tree的方式搜索，来进行计算，流程如图6所示。

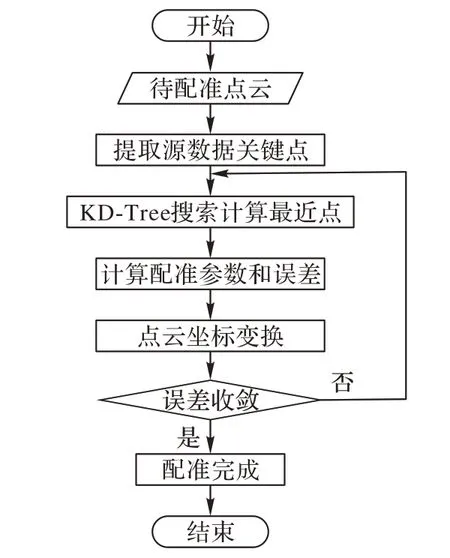
图6 改进ICP算法流程Fig.6 Flowchart of improved ICP algorithm

改进的ICP算法步骤如下：

1）对接骨板内曲面点云模型采用改进的内部形态描述算子（Insic Shape Signatures，ISS）算法提取特征关键点。

2）采用KD-Tree 的方式在胫骨选取区域查找与接骨板内曲面点的最近点，得到两组点云的初始对应关系。

3）根据步骤2）中的对应关系来计算两组点云之间的变换矩阵，使得目标函数（式（9））的值最小，并得到接骨板内曲面点在胫骨选取区域对应的点。

4）根据收敛条件判断两组点云之间的距离d是否小于设定的阈值μ：若d大于μ，且未达到设置的迭代次数，返回步骤2）继续迭代；否则迭代结束。

3.2.1 接骨板特征关键点提取

在进行精准匹配时，如果点云的规模庞大，则需要花费大量的时间进行计算，效率较低。为了在减少计算量的同时能保证计算的精确度，则需要对点云模型的特征关键点进行提取，本文针对接骨板内曲面点云模型进行特征关键点提取。

内部形态描述算子［23］能够高度区分点云模型的特征向量，对三维模型的几何特征进行编码，完成高质量的点云配准。接骨板内曲面点云边界作为曲面表达的重要几何特征，ISS 算法提取特征关键点时并不能较好地保留点云边界点。为此，在ISS 算法的基础上进行改进，在保留点云边界的基础上，对接骨板内曲面点云模型进行特征点提取，接骨板内曲面特征关键点提取算法流程如下：

1）对接骨板内曲的点bi及其邻域内的点（b1，b2，…，bn）做平面拟合，若向量bib1，bib2，…，bibn的方向偏向某一侧且向量之间的夹角最大值θmax小于阈值θτ，则将该点记为边界点。

2）计算接骨板内曲面点云模型中的每个点pi，以该点为中心、rd为半径的范围内点的权重为wi，wi与范围内点的个数成反比，表示为：

3）计算rd范围内所有的点pj(j=1，2，…，n)与点pi之间的协方差矩阵cov(pi)：

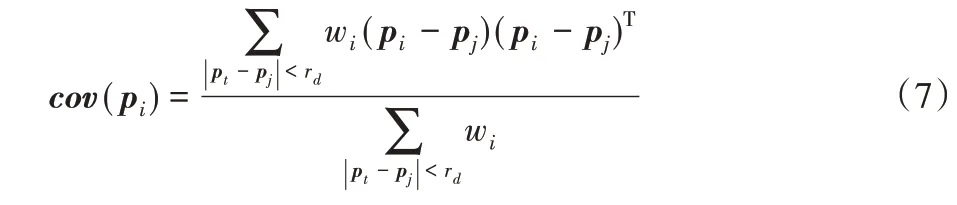
4）计算每个点pi的协方差矩阵的特征值｛λi，1，λi，2，λi，3｝并按照降序排列；

5）设定阈值ε1和ε2，ε1和ε2的范围在0～1，满足λi，2/λi，1≤ε1和λi，3/λi，2≤ε2的点即为特征点。

6）重复上述步骤，直至完成对接骨板内曲面点云模型内所有点的计算，得到接骨板内曲面点云模型的特征关键点。

对精简后的接骨板内曲面点云模型特征提取结果如图7（b）所示，从图中可以看出，提取的特征关键点能够很好地描述接骨板内曲面的几何特性，从而保证了接骨板内曲面与胫骨区域之间的高精度配准。

图7 特征关键点提取Fig.7 Extraction of feature key points

3.2.2 ICP配准

迭代最近点算法的本质是基于最小二乘法的最优匹配算法［24］，对于点云P中的n个点，使用一个3×3 旋转矩阵Ro和一个三维向量t来描述刚体变换。对于点云P中的任意一点pi(xi，yi，zi)和经过变换后的点，两个点满足以下条件：

重复选择对应的点qi来计算最优刚体变换矩阵T，直到满足最佳匹配的收敛精度，即使目标函数Ep最小化。

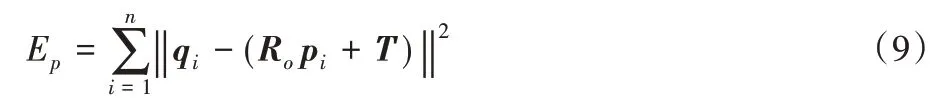
在解决ICP 算法对初始位置要求高和点云过于庞大的问题后，ICP 算法虽然能得到较好的配准效果，但是该算法本身的计算效率不高。而KD-Tree［25］是一种分割K维数据空间的数据结构，可应用于多维空间关键数据的搜索，且搜索具有搜索速度快的优点，因此本文采用KD-Tree 的方式对目标点云的空间进行搜索。

对接骨板内曲面模型的特征关键点与胫骨选取区域进行精确配准，配准结果如图8（b）所示，获取最终的变换矩阵Rs和三维向量ts，对接骨板模型Plate作变刚体换得到变换后的接骨板模型Plate'：

最终输出结果如图8（c）所示。

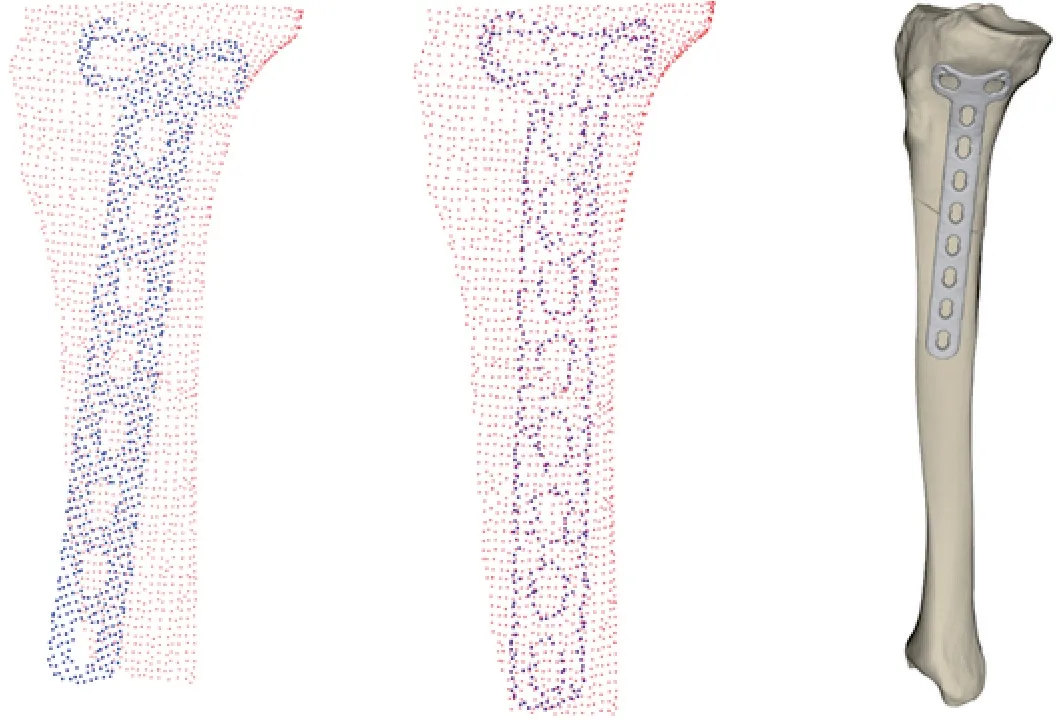
图8 接骨板配准结果Fig.8 Registration results of orthopedic plate

4 实验结果及分析

对本文所提算法在Microsoft Visual Studio 2019 平台进行实验，系统运行所需软硬件环境如下：操作系统Windows 7 及以上，内存2 GB或以上，CPU 2.1 GHz或以上。实验数据来源于课题组对断骨复位的研究和厂家扫描的接骨板模型数据，根据Schmutz等［5］提出的接骨板贴合性衡量标准，胫骨内侧接骨板和胫骨之间的间隙至少满足以下3 点要求：1）接骨板远近端近关节处距离骨面不超过2 mm；2）接骨板中部距离骨面不超过6 mm；3）接骨板近端距离骨面不超过4 mm。

文献［16-17］中都对传统的ICP 算法进行了改进，为了验证所提算法的实用性和有效性，将所提算法与ICP 算法、文献［16］算法、文献［17］算法进行比较，分别计算了接骨板远近端近关节处最大距离S1、接骨板中部与骨面之间最大距离S2，以及接骨板近端与骨面最大距离S3。以此为基础，在本文实验中接骨板贴合性定义为：1）当接骨板平均间隙小于2 mm 时，对应的贴合指数大于0.5，接骨板的贴合性为优；2）当接骨板平均间隙大于3 mm时，接骨板贴合指数小于0.3，接骨板贴合性为差；3）贴合指数在0.4～0.5的接骨板贴合性为良，在0.3～0.4 的贴合性为中。对匹配时间、平均间隙、贴合指数和贴合性进行记录，如表1所示。

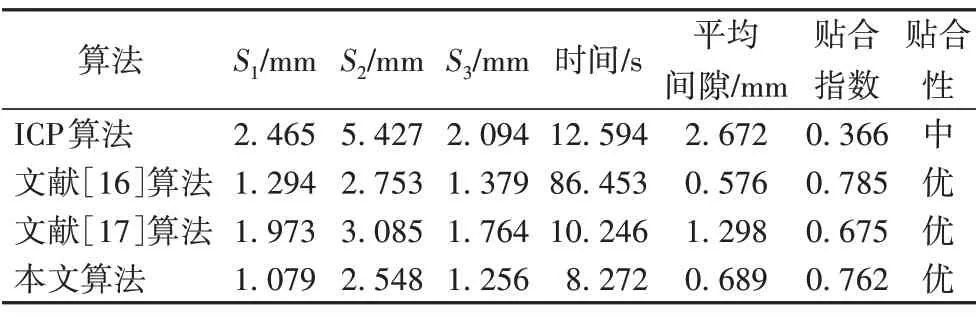
表1 不同算法所用时间和贴合性对比Tab.1 Time cost and fit comparison of different algorithms

由表1 中可以看出，本文算法与所对比的三种算法所得结果都满足Schmutz 等［5］提出的胫骨内侧接骨板和胫骨之间的间隙三点要求，但传统ICP 算法虽然能够在较短的时间内得到结果，但是贴合性较低；文献［16］算法虽然能得到较好的贴合性，但是计算时间过长；文献［17］算法虽然能够在短的时间内得到较好的结果，但与本文算法相比，本文算法所用时间更短且贴合性更佳。不同算法得到的最终输出结果如图9所示。

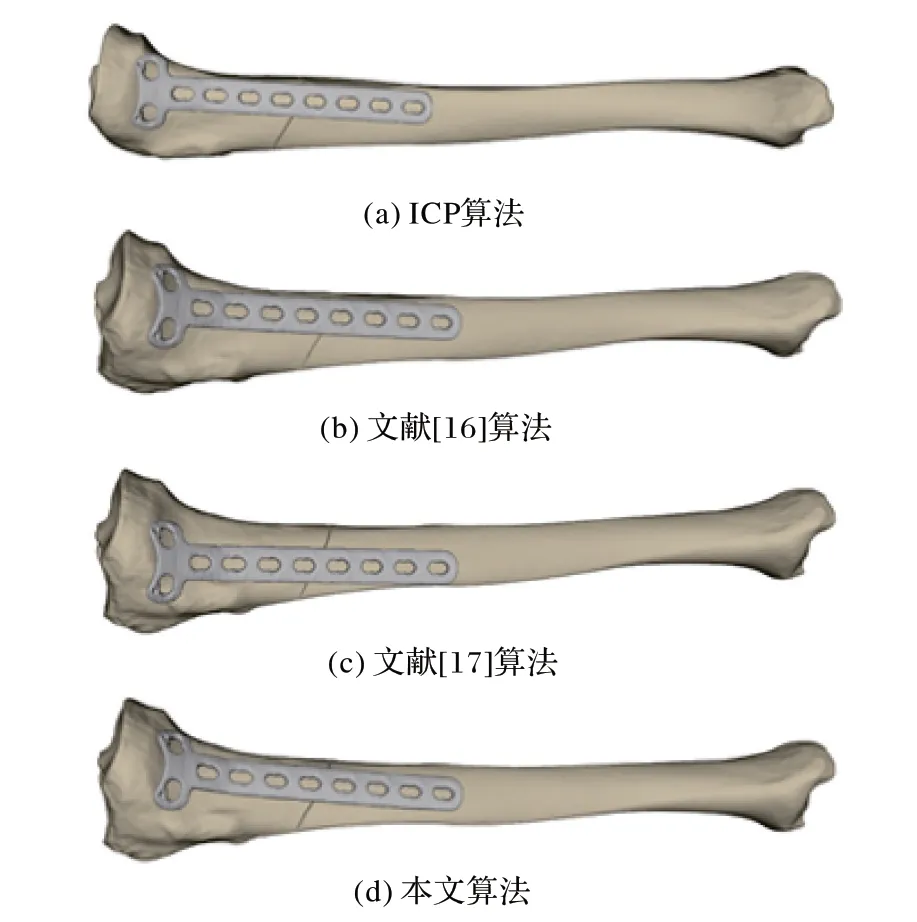
图9 不同算法配准结果对比Fig.9 Registration results comparison of different algorithms

为了验证所提算法的通用性，除了对胫骨近端受损和T形接骨板进行了实验，还对胫骨中端和远端受损分别选取两种不同类型的接骨板进行验证，实验所需配准时间、平均间隙和接骨板贴合性如表2所示。

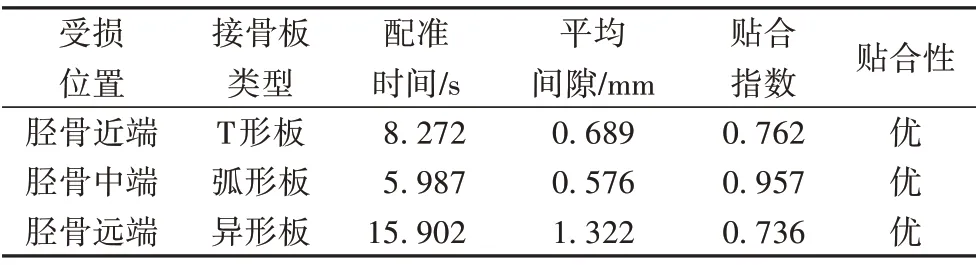
表2 不同受损类型和接骨板类型所用时间和贴合性对比Tab.2 Time cost and fit comparison of different types of damage and orthopedic plate

从表2 中可以看出，接骨板配准时间和贴合性主要与接骨板内曲面结构和接骨板选择的型号相关，对于内曲面结构简单的接骨板，如T 形、弧形等接骨板而言，所需的配准时间较短，接骨板的贴合性也较好；对于内曲面结构复杂的接骨板，如异形接骨板，所需的配准时间较长，平均间隙相对较大，但是仍在允许的最优间隙范围内。不同类型的配准效果对比如图10 所示，受损位置由矩形框标出，配准结果表明所选接骨板能够在选区的区域准确地找到贴合性最佳的位置。

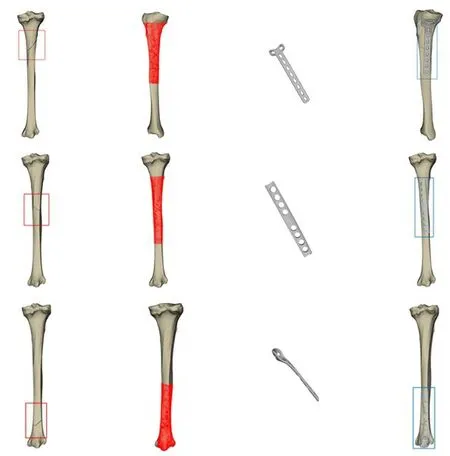
图10 不同受损类型配准结果Fig.10 Registration results of different damage types

5 结语

本文提出了一种基于改进ICP 算法的接骨板贴合性快捷计算方法，主要包括：选取贴合区域，提取接骨板内曲面点云；对两组点云平滑、采样，利用点云特征初始配准；提取接骨板特征关键点进行精确配准。本文方法的主要工作有：1）将配准过程分为初始配准和精确配准两步，配准效果更佳；2）对ISS 算法改进，使其能够同时获取点云边界和内部特征点；3）采用KD-tree 的方式搜索邻近点以提高ICP 算法的计算速度。通过对三种不同受损类型的胫骨和接骨板进行配准，实验结果表明本文所提算法能够高效、准确地计算出接骨板在胫骨上的最佳贴合位置。通过与其他配准算法作对比可以得出，所提算法在保证匹配精确度的同时能够有效缩短配准时间。本文方法为有效判断接骨板贴合位置提供了新思路，能够辅助医生更直观、高效地进行术前规划。未来将建立接骨板样本库，根据医生所选区域实现对接骨板型号自动选择，以更加高效、准确地计算接骨板贴合位置。