机械密封焊接金属波纹管随机振动响应及优化分析*

2021-11-04陶兴伟穆塔里夫阿赫迈德孙光耀张伟国

润滑与密封 2021年10期

陶兴伟穆塔里夫·阿赫迈德，2 孙光耀张伟国

(1.新疆大学机械工程学院新疆乌鲁木齐 830047；2.新疆大学电气工程学院新疆乌鲁木齐 830047)

机械密封因其泄漏量小、使用寿命长、工作可靠性能好，广泛应用在化工、石油等工业领域中[1]。焊接式金属波纹管作为机械密封的关键零部件，是一种高效实用的弹性元件，其结构的可靠性和稳定性直接影响到机械密封系统的安全性和使用寿命。机械密封系统在运行过程中，波纹管一直伴随有高温、高压、启停、冲击和振动等复杂载荷，其失效的主要形式不再是由单一的静强度破坏和动失效形式[2]。因此，对机械密封系统的关键零部件焊接式金属波纹管进行随机振动分析更为符合失效的实际情况。

国内外学者对机械密封波纹管进行了广泛研究。张清波等[3]认为波纹管密封性能受自身平衡影响，并通过改变焊接式波纹管的关键结构参数，研究不同的结构参数对平衡直径的影响。谭金等人[4]对焊接金属波纹管的波形对其刚度的影响进行研究，结果表明波片的不同位置的波形尺寸对波纹管的刚度有不同的影响。陈宇翔[5]通过对多层波纹管的刚度和振动的激烈程度进行数值模拟和分析，得到了通过改变波纹管的材料、壁厚和增大波峰来增加刚度。王升林等[6]针对波纹管产生的疲劳泄漏问题，研究了波纹管的焊接结构对波纹管使用寿命的影响。PIERCE和EVANS[7]对处于循环载荷下的金属波纹管的失效进行分析。PAVITHRA和KUMAR[8]采用有限元方法研究了室温与高温环境下的波纹管径向应力变化规律，得到波纹管的失效是由于持续工作时产生高温环境所致。赵文元等[9]针对波纹管在实际工况下的失弹、疲劳失效等现象进行研究，得到温度和力对波纹管在工作中的失效影响较大。

目前，国内外学者对焊接式金属波纹管研究主要集中在对波纹管的密封性能、失效原因、使用寿命和波纹管的刚度进行分析。由于波纹管在工作中所受到的载荷是随机的，其运动规律无法用确定的本构方程进行表述，所以对机械密封波纹管在随机激励下的振动特性研究的很少见。针对焊接式金属波纹管在工作中出现的随机振动问题，本文作者运用虚拟激励法理论，分析波纹管激励下的振动特性，为波纹管的设计和可靠性分析提供参考。

1 波纹管动力学模型及振动模态分析

1.1 波纹管动力学模型

在焊接式金属波纹管中，波纹管位于前环和后环之间，其结构示意图如图1所示。

图1 波纹管结构Fig 1 Structure of bellows

由于金属波纹管是一个复杂结构的多自由度的系统，且在振动时其角位移很小，可忽略其转动惯性，在有限元分析中通常将其结构简化成用质点、弹性元件和阻尼器等构成[10]。简化力学模型如图2所示。图中，k1、k2为动态刚度，c1、c2为等效阻尼系数，m1、m2、m3分别为前环、波纹管、后环的质量。

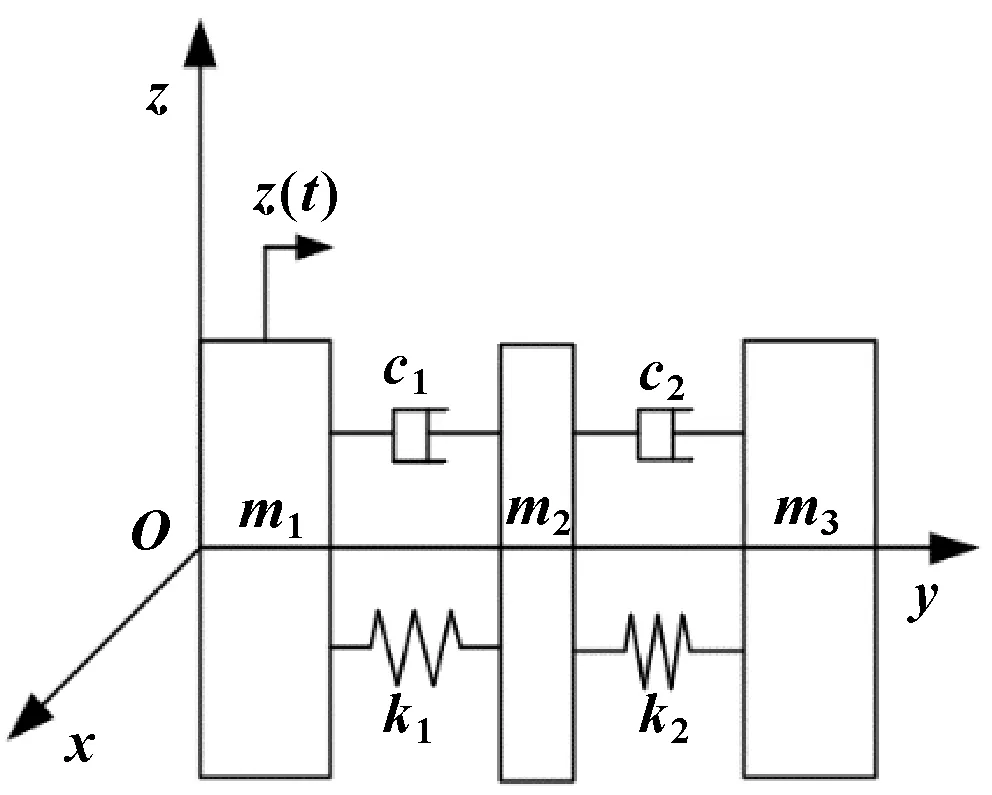
图2 波纹管简化力学模型Fig 2 Simplified mechanical model of bellows

1.2 振动模态分析

模态分析法的目的是得到固有频率和振型，从而在机械密封系统的动力性能设计时，避免波纹管运转过程中与机械密封系统发生共振，影响使用寿命。

由振动理论和有限元模态分析理论知，多个自由度的弹性振动系统其结构振动的动力学通用方程为

(1)

在对结构的自由振动的固有频率和振型求解时，阻尼对其影响极小，可以忽略不计。由于在模态分析时，没有力的作用即F(t)={0}，故可得到无阻尼的结构振动运动方程[11]：

(2)

则其特征方程为

(K-ω2M)M={0}

(3)

式中：ω表示系统的固有频率。

2 波纹管载荷的虚拟激励

假设该系统为线性系统，则所受到的自功率谱密度为Sxx的平稳随机激励为x(t)，其对应响应y的自功率谱为

Syy=|H|2Sxx

(4)

式中：H为频率响应函数。

由于用传统的方法进行随机振动响应分析会受到计算效率的影响且计算比较繁琐，而虚拟激励法[12]的提出将平稳的随机振动分析转化成简谐振动分析。

考虑到波纹管的弹性体受到单元同相位的平稳随机激励，运动方程为

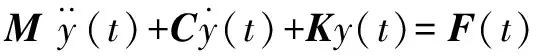
(5)

式中：M、C、K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；F(t)=pf(t)，p为力矢量；f(t)为平稳随机作用力，其自功率谱为Sff(ω)。

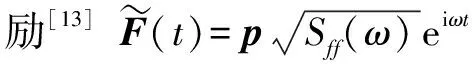
(6)

其中，“～”表示虚拟激励下的结构响应。此时，式(6)中的激励由平稳的随机响应激励转化成谐响应激励。可得到波纹管在虚拟激励下的位移响应为

(7)

式中：H(ω)为频率响应矩阵。

由虚拟激励法求得的位移功率谱矩阵为

(8)

3 波纹管的振动特性分析

3.1 数值模态分析

文中研究的是DN55号波纹管，其材料属性如表1所示。

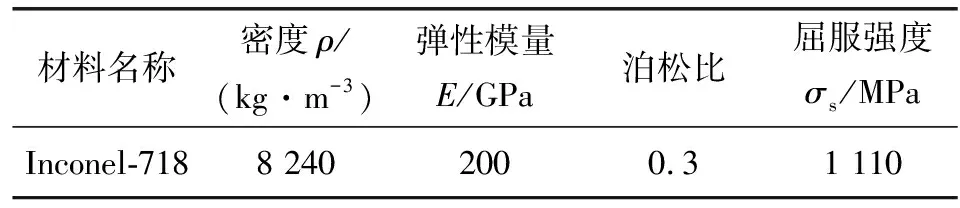
表1 DN55号波纹管材料属性Table 1 Material properties of DN55 bellows

由于波纹管的前环与静环镶嵌为自由端，后环与压盖相连为固定端，故施加的边界条件为一端固定，另一端自由[14]。结合商用分析软件对波纹管进行模态分析，得到的固有频率和振型如表2所示。

表2 波纹管前10阶固有频率Table 2 First 10 natural frequencies of bellows

在结构模态分析中，模态有效质量提供了一种方法用于判断模态重要性[15]，模态有效质量越高越容易被外界激励起来。在前10阶模态分析中，超过70%的模态有效质量在前10阶模态中，高阶的有效质量占比较小，则不容易被外界激励起来。由表2可以看出，波纹管的固有频率随着阶数的增加而增大，无规律可循，表现出无阻尼振动的随机性；前10阶振型主要是以弯曲、轴向、折叠和挤压等振型的形式表现，其中在前10阶中，有4组模态频率相同说明了轴对称结构存在多对重根且相对密集。

3.2 随机振动响应分析

随机振动分析即功率谱密度分析(Power Spectral Density,PSD)，是一种基于概率统计学的谱分析方法。PSD是结构在随机载荷激励下的概率统计结果，包括位移功率谱密度、速度功率谱密度和加速度功率谱密度。文中在模态分析的基础上，根据虚拟激励法理论，使用MATLAB汇编语言对波纹管在随机激励下的轴向和径向进行时域分析，对其进行快速傅里叶变换，将时域转化成频域，得到功率谱密度，再结合商业分析软件Workbench进行数值仿真计算。

由MATLAB汇编语言编程得到的波纹管在稳态时随机激励的轴向和径向振动随机响应如图3和图4所示。

图3 轴向位移Fig 3 Axial displacement

图4 径向位移Fig 4 Radial displacement

由图3和图4知，波纹管的振动位移均呈现随机性和不可预测性，轴向振动位移范围在-0.5～0.5 mm,小于径向振动位移范围-4～4 mm，这与文献[16]通过试验得到的结果相一致，同时也说明了文中对波纹管动力学建模的正确性和方法的可行性。轴向位移较小，在工作过程中会出现静环与动环之间的位移差，会出现瞬态碰撞从而造成镶嵌在静环上的石墨环的破损；而径向位移较大，在工作过程中，由于存在动环与静环之间位移差，导致其出现接触磨损，密封性能降低。

采用Periodogram函数将时域信号转化成振动位移功率谱密度分别对轴向和径向进行分析。图5和图6分别示出了波纹管轴向和波纹管径向位移功率谱密度。结果表明：波纹管的轴向和径向的能量都集中在190～240 Hz之间，且径向的能量远大于轴向的能量，这是由于在安装时轴向有预应力且只有一个自由度，在工作时不易释放能量，而波纹管为旋转体，径向自由度多，能更好地释放能量；波纹管外界激励的频率在190～240 Hz范围内且介于模态分析结果1阶频率190.89 Hz和3阶频率241.09 Hz之间，工作在此激励下容易发生共振现象，因此，在对波纹管的设计时要注意一阶、二阶和三阶的振动形态对波纹管结构的影响。

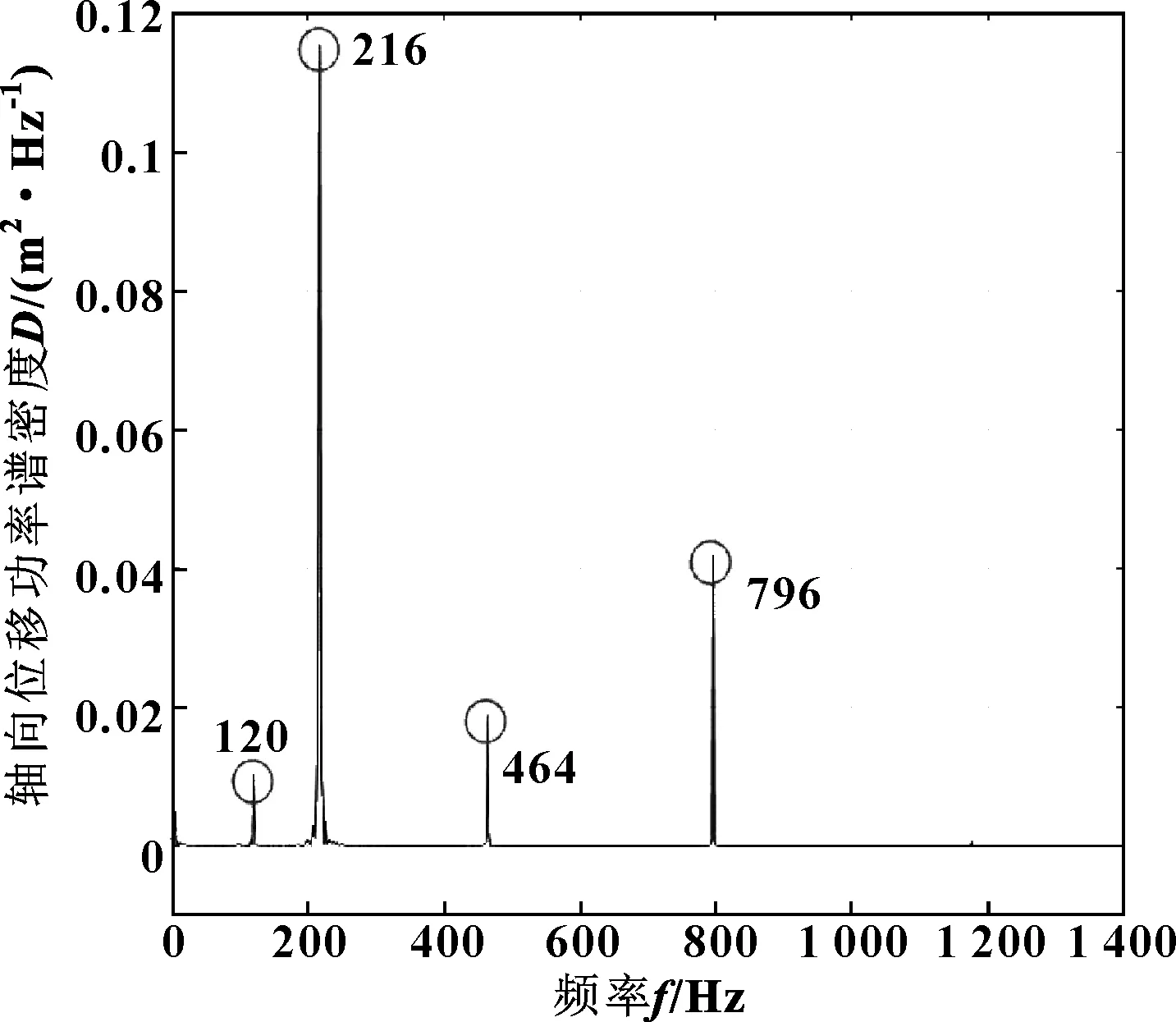
图5 波纹管轴向位移功率谱密度Fig 5 The power spectrum density of the axialdisplacement of the bellows

图6 波纹管径向位移功率谱密度Fig 6 The power spectrum density of the radialdisplacement of the bellows

由于径向位移功率谱密度整体大于轴向功率谱密度且能量较大，其对结构具有较大的影响作用，故取径向位移功率谱密度作为输入位移功率谱密度，结合商用分析软件Workbench对波纹管进行随机振动分析。图7所示为波纹管轴向变形云图，图8(a)和图8(b)所示分别为径向变形应云图和径向变形局部放大图。

由图7可以看出，波纹管轴向最大变形发生在镶嵌静环的一端即自由端，并且沿轴向且靠近固定端的位移响应呈递减趋势。这是由于波纹管的弹性自由端在运动过程中刚度得到了释放。从图8可以看出，整体径向位移响应具有对称性，将波纹管分成4个对称部分，体现出对称结构的对称性；径向变形最大点发生在靠近波纹管的固定端的波片弧度较大处。这些位置在工作过程中最容易损坏，设计时应进行优化。

图7 轴向变形云图Fig 7 Contour of axial deformation

图8 径向变形云图及局部放大图Fig 8 Contour of radial deformation(a) anda partial enlarged view(b)

图9和图10所示分别为波纹管轴向和径向载荷下的等效应力云图。可以看出在随机振动下的等效应力分布主要集中在靠近波纹管膜片焊接处的焊箍处，轴向载荷下的最大等效应力为976.23 MPa，小于径向载荷下的最大等效应力1 096.3 MPa。此处的等效应力较大，是应力集中发生的主要位置，容易发生固定端波纹管断裂，与在实际工作中的破坏位置相一致。为提高波纹管的使用寿命，在设计过程中应该对该处进行优化。

图9 波纹管在轴向载荷下的等效应力Fig 9 Equivalent stress of bellows under axial load

图10 波纹管在径向载荷下等效应力Fig 10 Equivalent stress of bellows under radial load

4 响应面优化分析

优化分析的目的是满足波纹管正常的运转过程中降低随机振动响应，减小在外界激励下的变形量，延长波纹管的使用寿命。

文中优化分析采用的是Ansys Workbench中响应面优化方法(Response Surface)。通过改变波纹管的部分结构参数来改变波纹管在随机激励下的响应。以单个V形焊接式波纹管波片的厚度P1、最小弯曲半径P2和两波片的焊箍半径P3为优化变量，如图11所示；以单个波片在虚拟激励下的径向变形量P4和等效应力P5作为目标变量，求解出它们的最小值，即min(P4、P5)。各物理量的初始值如表3所示。

图11 波纹管波片优化变量Fig 11 Optimized variables of the bellows wave plate

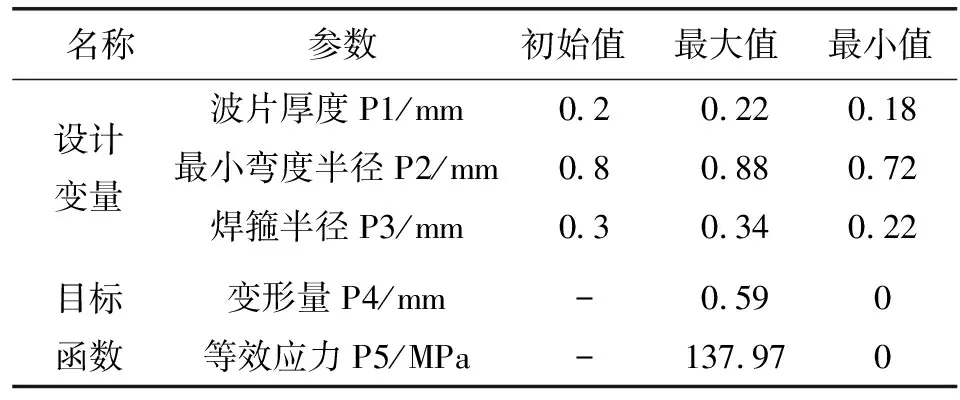
表3 波片设计变量及初始范围Table 3 Waveplate design variables and initial ranges

4.1 灵敏度分析

通过响应面分析可得到不同的设计参数对不同的输出变量的灵敏度，同时，灵敏度可以作为输入参数对输出参数影响的参考评定。为得到输入变量对目标函数的可靠程度，采用Box-Behnken方法进行仿真试验得到目标函数的局部灵敏度。局部灵敏度分析结果如图12所示。可知，P1、P2和P3为正值，对P4正相关；P1、P2和P3对P4的影响依次减小；P1和P2对P5为正相关，P3对P5为负相关。目标函数P4和P5所对应的设计变量均有正有负，对设计变量来说，并不是增加或降低某一变量就能改变P4和P5，合理地选择结构参数很有必要。

图12 局部灵敏度分析Fig 12 Local sensitivity analysis

4.2 响应面分析

由试验结果可得到设计变量与目标函数之间的响应曲面，如图13所示。从图13(a)可知，P1和P2对波片的变形量(P4)呈正相关趋势，但在曲面增长的同时也出现较大波动，这是由于V形焊接式波纹管的波片变形还受到其他较小结构参数的影响。从图13(b)可知，波片厚度(P1)与等效应力(P5)呈正线性关系，减小波片厚度能减小等效应力。减小波片的厚度可以降低波片的变形和等效应力，同时适当地减小焊箍半径有助于减小变形，适当地增大最小弯曲半径可以降低等效应力。

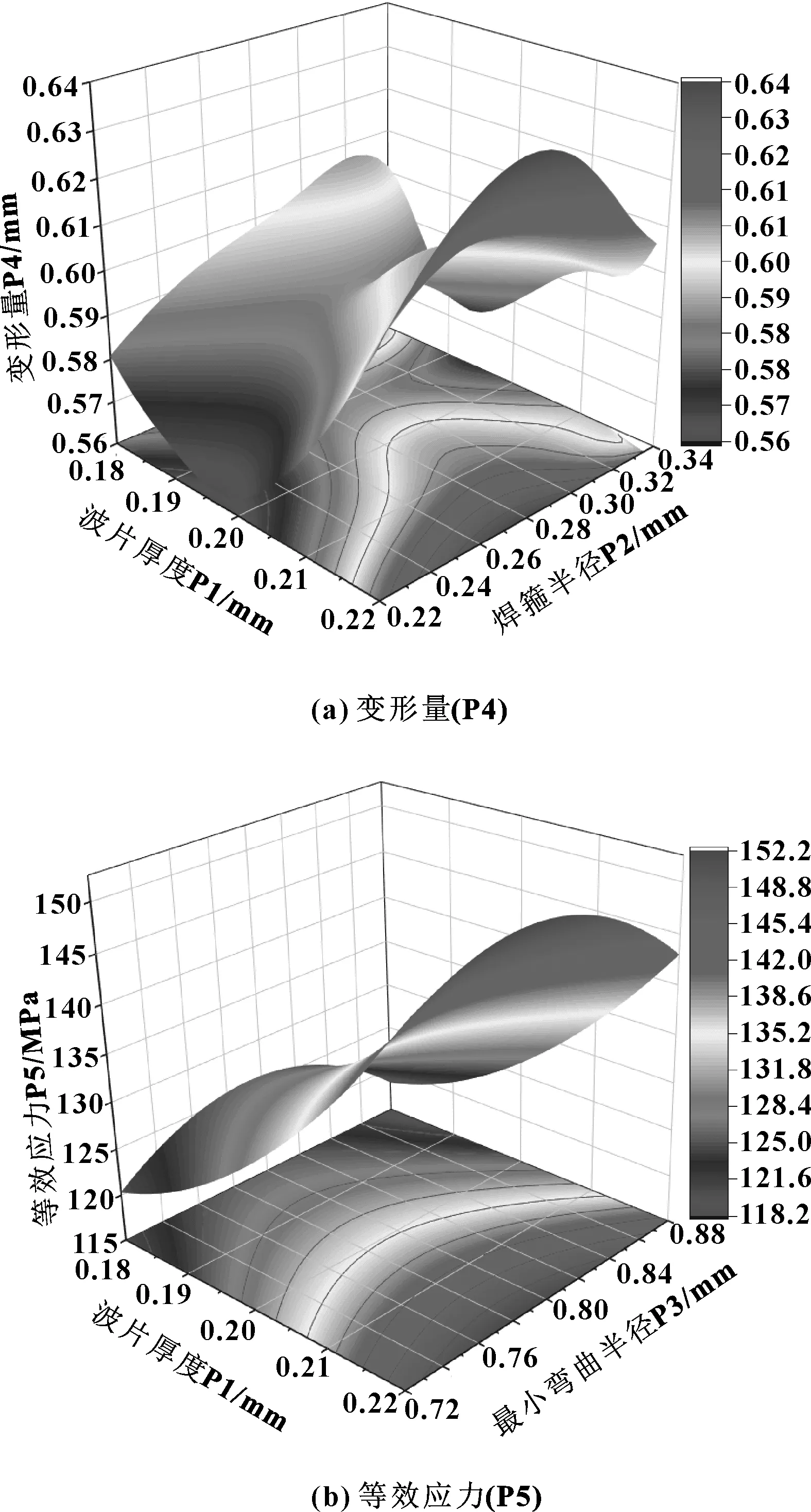
图13 响应曲面分析Fig 13 Response surface analysis (a)deformation(P4);(b)equivalent stress(P5)

4.3 优化结果分析

由灵敏度分析和响应面分析得到P1、P2、P3对所求的目标函数有较大的影响。为了降低目标值，因此采用自适应多目标优化法(Adaptive Multiple-Objective，AMO)对其进行优化分析。最终，在生成的617组样本中筛选评估出3组优化方案如表4所示。

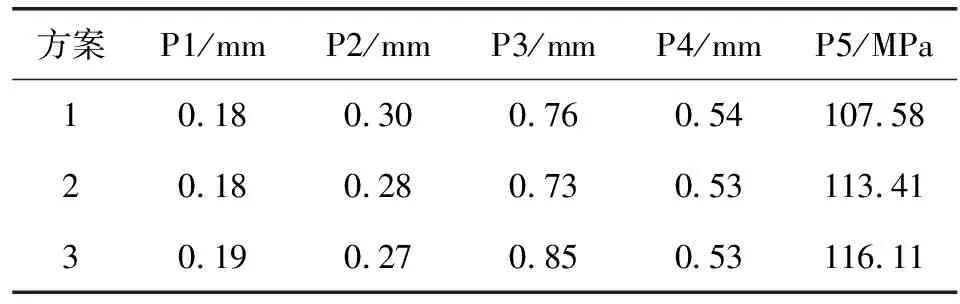
表4 优化方案Table 4 Optimization schemes

基于表4中的3种优化方案，结合实际工程中零部件的损坏情况，以波纹管在运转过程中变形量最小和适当减小等效应力为目标，选取优化方案2作为最佳方案。对比优化前后V形波片变形量和等效应力可知，优化后波片的变形量减小10.17%，等效应力减小12.65%。

优化前后波纹管的固有频率如图14所示。可以看出，优化后波纹管的前5阶固有频率有一定减小。固有频率降低，可避免波纹管在工作中受外界随机激励而发生共振，从而提高波纹管的振动特性。

图14 优化前后波纹管固有频率对比Fig 14 Natural frequency comparison of bellowbefore and after optimization

优化后波纹管的变形量和等效应力如图15(a)、(b)所示。波纹管运转过程中，受到流场随机激励导致波纹管的振动，其实质是波纹管在循环作用下形成的振动疲劳导致。优化后波纹管的最大变形量减小64.96%，整个波纹管的最大等效应力减小1.94%。波纹管等效应力降低较小是因为波纹管变形较大，能更好地吸收波纹管在变形时释放出的能量。优化后的波纹管能更好地抵抗外界干扰而产生的变形，具有更高的抗破坏能力，使用寿命更长。