基于密封缝隙非线性特性的车内外压力传递模型研究

陈春俊，冯永平，何智颖，李 明

(1.西南交通大学 机械工程学院，四川 成都 610031；2.轨道交通运维技术与装备四川省重点实验室，四川 成都 610031；3.中车唐山机车车辆有限公司 技术研究中心，河北 唐山 064000)

随着中国高速铁路网络的不断完善，高速列车运行里程的不断增加，中国高速列车以跨越式的速度挤进世界前列，但是仍存在一些问题亟待解决。其中之一就是乘车过程中的气压舒适性问题，尤其在高速通过隧道时最为严重，列车通过隧道时，由列车-隧道耦合产生的隧道压力波传入车内，引起剧烈的车内压力波动甚至会造成乘客头晕、恶心[1-3]。因此，为了保障司乘人员的乘坐压力舒适性要求，国内外已经制定了相对完善的气密性标准用于指导高速列车的生产制造[4-5]。但随着气密性标准的提高，车体的制造成本也随之增大，需要对高速列车压力保护控制系统提出新的要求。因此，对车内外压力传递模型进行研究，预测计算高速列车动态运行情况下车内压力峰值及其变化规律，对压力舒适性标准的制定以及车内压力控制系统的优化设计具有指导意义。

目前，国内外对隧道工况下客室内外压力传递模型进行了大量研究工作。文献[6]对比分析了时间常数法模型、流动模型、等效泄漏模型的可行性；文献[7]基于等效泄漏面积，根据流入流出车厢的流量关系，建立了车体气密性模型；文献[8]基于车体气密性标准及风机特性，研究了车体缝隙、换气风道处质量流量与内外压力的关系，根据质量守恒建立了车体内外压力传递模型；文献[9]参照客室内压力舒适性标准，研究了高速列车以400 km/h速度通过隧道时满足人耳舒适性的动态气密性阈值，以此为气密性车体的制造提供参考;文献[10]基于车内外压力传递模型，结合高速列车通过隧道的实测数据研究了动态气密性与隧道长度、速度的关系；文献[11]基于密封指数定义得出列车内部压力与车内外压差的线性关系，并研究了车内压力波动与人耳舒适性的情况；文献[12]求解定义密封指数的微分方程，得出车内压力关于车外压力的非线性关系，研究了密封指数与车内压力变化率的关系；文献[13]根据等效泄漏模型对车内压力波动进行预测控制，进而对车厢内压力保护系统的优化设计提供参考。

从上述分析可以得出，等效泄漏面积能够直观地反映车体气密性能，而且这种车内外压力传递模型从质量守恒的角度出发，方便与车体换气系统的通风量耦合建立更加精确的车内外压力传递模型，但是基于等效泄漏面积的车内外压力传递模型中气密参数(等效泄漏面积)通常是根据静态气密性试验标准确定的常数，其等效泄漏面积忽略了密封缝隙在不同压差下的非线性特性[6-8]。

为此，本文根据静态气密性试验数据，研究分析车体密封缝隙在不同内外压差下的变化规律，并结合密封缝隙的非线性特性建立车内外空气经密封缝隙的质量流量；根据高静压风机特性曲线建立换气系统的空气质量流量与内外压力的关系式，基于质量守恒和绝热等熵假设，耦合密封缝隙、换气风道系统建立了考虑密封缝隙非线性特性的车内外压力瞬态传递模型。最后采用实测隧道内外压力波数据对动态气密性模型进行了模型矫正和验证。

1 高速列车密封缝隙变化规律研究

1.1 高速列车气密性评估方法

高速列车新车落成出厂前会进行一次整车气密性试验，试验过程中将换气系统封堵。广泛采用的TB/T 3250—2010《动车组密封设计及试验规范》[14]规定：车内压力由4 000 Pa自然衰减至1 000 Pa时间不小于50 s。

日本铁道科学技术研究所采用等效泄漏面积与车厢体积的比描述列车的气密度，等效泄漏面积即将车体门、窗、风挡等密封缝隙等效成统一的泄漏面积表征，等效泄漏面积与车内外压力的关系为

(1)

式中:S为等效泄漏面积；V为车厢体积，135 m3；ΔP0为初始压差，通常取4 kPa; ΔPt为截止压差，通常取1 kPa;t为车内外压力差从ΔP0泄漏到ΔPt的泄漏时间，s。

等效泄漏面积是能够直接反映列车气密性能的物理量。由式(1)可以看出，等效泄漏面积是由初始压差、截止压差以及泄漏时间确定的时均值，忽略了密封缝隙在不同压差下的非线性特性。

1.2 等效泄漏面积研究方法

车体密封缝隙的非线性特性可以根据静态性试验开展，高速列车静态气密性试验可以使用静态泄漏模型进行很好地描述，见图1。

图1 静态泄漏模型

将门窗、风挡及焊缝等密封缝隙等效为一种缝隙类型，车内外空气流动为无黏流动，根据伯努利能量方程及质量守恒定律可知[13]

(2)

(3)

式中:m为车内空气质量,kg;qm为质量流量,m3/h;ρ为空气密度，kg/m3;Pi为车内压力，Pa；Pe为车外压力，Pa。

假设静态气密性试验中气体流动过程是绝热、等熵的，则

(4)

将车内压力变化梯度用一阶线性差分表示，并将其代入式(4)，可得

(5)

式中:γ为空气的比热容比，取1.4；R为气体常数，R≈287 J/(kg·K)；T为环境温度，静态气密性试验在室内进行，室内环境稳定，测试温度是301.65 K。

1.3 等效泄漏面积变化规律

在进行静态气密性测试车厢的端部和中部设置2个测点，同时在车厢中部测点对应的车外位置设置测点，试验过程中采用的压力传感器是Endevco 生产的高精度贴片式压力传感器。高速列车静态气密性试验记录的2组车内压力实测数据见图2。

图2 整车气密性试验车内压力测试记录数据

根据式(5)，可以计算得到静态气密性试验过程中车体等效泄漏缝隙随时间变化曲线，将其与车内压力曲线一一对应，则可得知车体密封缝隙在不同车内外压差下的变化曲线，见图3。高速列车车体缝隙在负压差下的变化趋势较正压差要缓慢一些，即当车内压力小于车外压力时，高速列车表现出较好的气密性能；车内外压力差的绝对值在0 ～ 0.5 kPa时，车体的等效泄漏面积呈指数增加；车体内外压差值在-4.5 ～ -0.5 kPa、0.5 ～ 3.2 kPa时车体的等效泄漏面积近似线性变化；当车内外压力差的范围为3.2 ～ 4.5 kPa时，等效泄漏面积近似是指数变化。

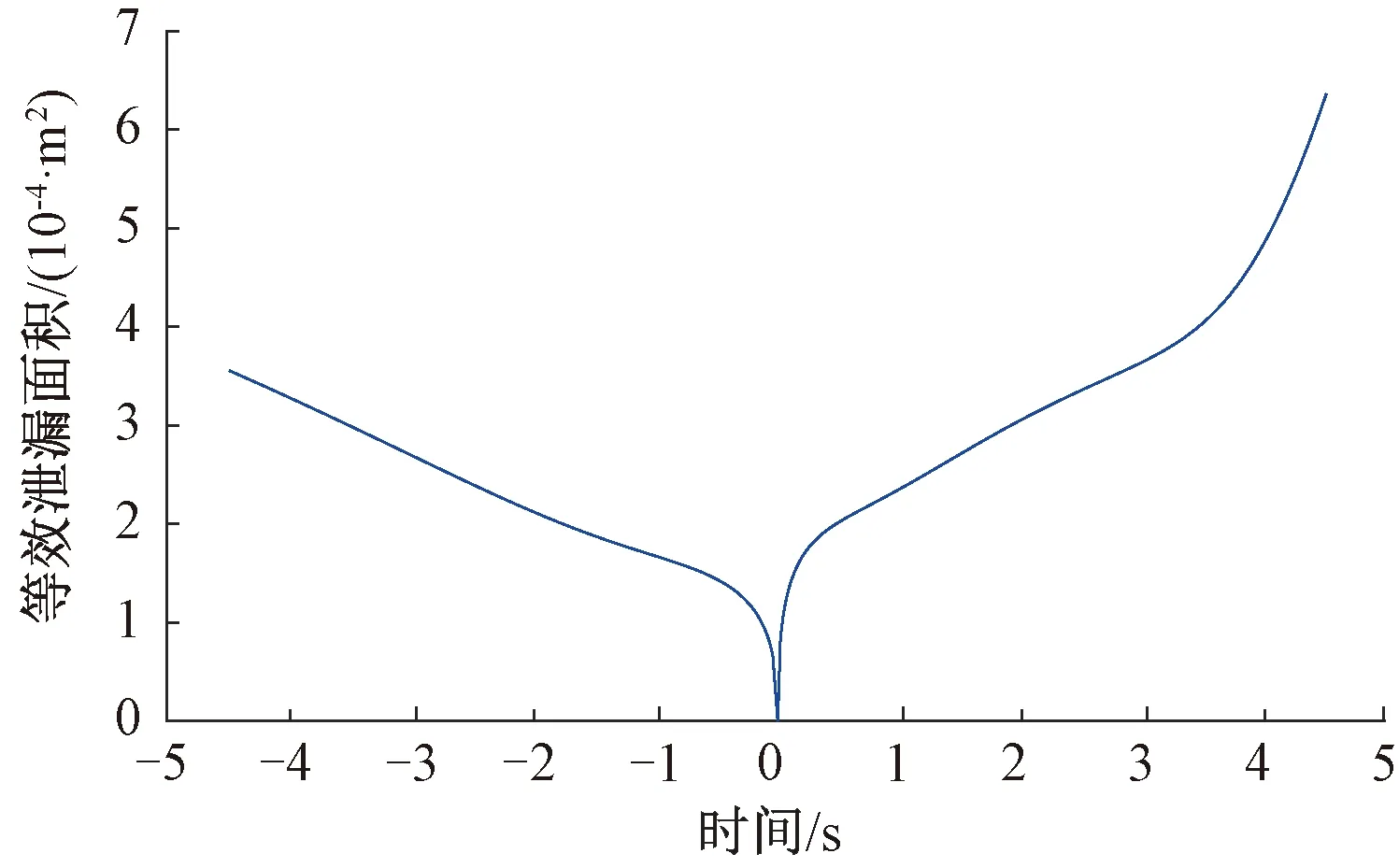
图3 车体密封缝隙随压差的变化曲线

2 车体内外压力与空气质量流量间关系

等效泄漏面积可以直接反映车体的密封性，并且从流入流出车厢流量的角度出发，容易将车体气密性与车体换气系统耦合在一起，建立考虑密封缝隙非线性变化的车内外压力传递模型。

目前，国内外学者研究表明影响车内压力变化的因素主要有车体刚度、密封缝隙及通风换气系统。气动载荷作用于车体表面改变形状进而影响车内压力，当综合考虑换气风道、车体气密性和车体刚度时，车内外压差小于完全封闭车体的情况，车体变形被削弱，车体结构变形对车内压力的影响甚微，可以忽略[15]。所以模型主要考虑车体密封性和车厢换气系统二种因素：①由于门、窗等部件的安装缝隙以及焊接缝隙等构成，根据密封缝隙在车内外压差下的非线性特性，建立泄漏缝隙处空气流量与车内外压力的传递关系；②高速列车在运行过程中，为保障车内空气清新，换气系统处在打开状态，因此基于风机特性曲线以及广义的风道特性曲线的动平衡关系建立风机风量的数学模型。

2.1 车体密封缝隙处质量流量关系

由于高速列车制造过程中存在一定的密封缝隙，在高速列车通过隧道时，由于车厢内外压力差的作用，在车体密封性不足处，进行空气质量交换。

车厢的泄漏缝隙及其泄漏途径特别复杂，很难进行具体的数学描述，所以从宏观角度出发，假设车体缝隙是一个总的泄漏缝隙。并假设气体为无黏气体，当车内压力Pi大于车外压力Pe，车内空气通过泄漏缝隙向车外流动，在车体密封缝隙处，根据伯努利方程可得

(6)

式中:ρi为车内空气密度，kg/m3；vi为车内空气流速，m/s；Zi为车内缝隙高度，m；ρe为车外空气密度，kg/m3；ve为车外空气流速，m/s；Ze为车外缝隙高度，m；g为重力加速度，通常取9.8 m/s2。由于气体质量较小，空气流动过程中，往往忽略其重力势能的影响，而且车体泄漏缝隙远远小于车厢体积，泄漏缝隙内的流动不会对客室状态产生影响，故vi=0，则

(7)

车内外空气通过密封缝隙的质量流量可以用缝隙大小出口的速度及车外空气密度求得

qm=S(ΔP)veρe

(8)

式中:S(ΔP)是由车内外压力确定的等效泄漏面积,m2。

根据理想气体状态方程

(9)

式中:P为压力，Pa。

当车内压力大于车外压力时，将式(7)、式(9)代入式(8)，则通过高速列车密封缝隙的空气质量流量为

(10)

同理可求出车外压力大于车内压力时，车体密封缝隙处的质量流量，可得

(11)

2.2 通风换气系统数学模型

高速列车通风换气系统由新风机、废排风机及送回风管道组成，新风机、废排风机特性及参数相同。根据高静压风机的连续换气特性，即风机压头等于通风管道内外压差与风道压力损失之和，文献[8] 推导了高速列车通风换气系统的通风量与车内外压力的数学关系为

(12)

(13)

3 高速列车动态模型及验证

3.1 高速列车动态模型

假设车体为刚体，车体体积不随内外压力差变化。已知通过车体密封缝隙进出车厢的空气流量和列车通风换气系统的换气风量与车内外压力的关系。以车厢为研究对象，根据质量守恒定律，可得

(14)

假设车体内外空气的交换过程是等熵绝热的，将式(14)代入式(4)，则

(15)

实测车外压力采用频率为f，则dt=1/f；根据梯度定义可得

(16)

式中:k为离散时刻，对应的连续时刻t=kf。列车运行过程中，车厢压力保护系统装置(即通风换气风机)需要根据瞬时的车内外压力环境对风量进行及时的调整，并通过换气风道管路传递至车内，这个传递过程存在一定的响应时间，故在建立车内外压力传递模型时，考虑延时时间n，则基于密封缝隙非线性特性的车内外压力传递模型可表示为

(17)

采用高精度贴片式压力传感器、IMC采集器、DPS 电源等设备搭建便捷式车载采集设备，同步测试得到高速列车通过隧道时，位于车厢中部且距离车厢地面高1 m处内外测点的压力数据，对式(17)进行拟合校正，求得延迟时间n=5。

3.2 模型验证

使用某型号高速列车通过不同隧道时的车体外表面压力数据，根据式(17)推算车内压力数据，见图4。由图4可以看出，计算得到的车内压力数据与实测的车内压力数据基本一致，证明模型的可行性。

图4 列车通过隧道时车内外实测压力曲线与车内仿真曲线

根据车体密封缝隙随压差变化关系，可以计算得到某高速列车通过隧道时密封缝隙的变化规律，见图5。隧道工况下车体的密封缝隙变化与实测的车内外压差曲线波形相似，幅值相反。日本铁道技术研究所给出了车体缝隙的等效面积与车厢内外压力的关系，并将2S/V称为气密度。日本根据原气密性试验标准，即车内压力由400 mmH2O降至100 mmH2O的时间不少于40 s，代入式(1)得到气密度2S/V≤0.25[1]。列车通过1#隧道时车体密封缝隙最大为3.157 1 cm2，气密度为0.046；列车通过2#隧道时车体密封缝隙最大为3.102 7 cm2，气密度为0.045；高速列车通过1#、2#遂道的气密度都小于0.25,满足气密性指标；高速列车在1#隧道时的乘坐舒适性略差于通过2#隧道时的乘坐舒适性。

图5 列车通过隧道时车体密封缝隙变化曲线

4 结论

(1)本文采用静态泄漏模型，基于高速列车静态气密性实验数据，研究了不同压力差作用下的车体密封缝隙的非线性特性，由于高速列车密封件的单向可通过性，车体在负压差下表现出较好的密封性。

(2)结合车体密封缝隙在-4.5 ～ 4.5 kPa压差下变化曲线，建立密封缝隙处空气泄漏量与车厢内外压力的关系模型，耦合换气风机空气流量与车厢内外压力的数学模型，基于质量守恒和绝热等熵假设建立考虑密封缝隙非线性特性的车内外压力传递模型。

(3)采用某型号高速列车通过不同隧道时的车内外实测压力数据对考虑密封缝隙非线性变化的车内外压力传递模型进行验证，证明了模型的可靠性，并且高速列车车体等效泄漏面积在隧道工况下的波形变化与车内外压差波形相似，通过2#隧道时的乘坐舒适性优于通过1#隧道。