基于故障物理和数理统计相结合 的可靠性加速试验方法

李墨，孙瑞锋

（1.中国电子科技集团公司第二十九研究所，成都 610036；2.中国航空综合技术研究所，北京 100028）

现代高新装备对可靠性水平提出的要求越来越高，其中起关键作用的电子/机电/光电等产品向数字化、小型化、密集化、多功能化以及复杂化方向发展，其可靠性要求也更高。许多产品的可靠性指标平均故障间隔时间（MTBF）要求达到数千甚至上万小时，按照传统的可靠性试验技术进行试验，所需的试验周期长、试验费用高，在实际工程中难以接受。因此，面对高可靠性装备研制周期短、经费高的特点，现有的基于环境模拟的传统可靠性统计试验方法和评估技术，由于时间长、经费高，已不能满足产品研制要求。采用加大试验应力、缩短试验时间的可靠性加速试验技术，已成为可靠性验证试验技术发展的必然趋势[1-4]。

现有的定量可靠性加速试验方法主要建立在经验基础之上，对产品施加何种应力，取决于对产品主要故障机理的了解。目前常用的加速试验模型均是基于元器件故障机理的统计加速模型[5-12]，加速模型未考虑应力在产品结构中的传递作用，模型的准确度相对较低。目前装备研制中开展了较多的可靠性仿真分析工作，获取了热和振动应力对产品影响的大量信 息。如何将这些信息应用到可靠性加速试验中，更好地设计加速试验方案，是目前工程实际急需解决的一个问题。

1 故障物理分析及加速应力量值的确定

在制定可靠性加速试验方案之前，首先需要对受试产品进行故障物理分析。故障物理分析的目的是了解产品在寿命周期环境条件下可能的故障模式、故障机理、故障位置和故障时间，从而为产品主要故障机理、加速试验条件和加速模型或加速因子的确定创造条件。

建模与仿真方法是开展故障物理分析最为全面有效的方法，它结合了产品的具体设计特性，完整地考虑了寿命周期环境及工作载荷的影响方式，详细地定义了产品的故障。同时，考虑了制造过程中工艺参数对建模影响，通过模型输入参数的随机特性，科学地考虑了随机因素对可靠性的影响。基于故障物理的可靠性仿真分析的基本流程如图1所示。

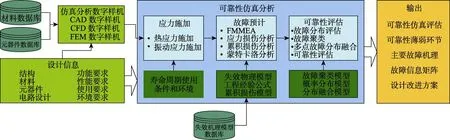
图1 基于故障物理的可靠性仿真基本流程 Fig.1 Reliability simulation basic flow based on fault physics

产品存在其工作应力裕度，当试验应力水平在工作应力裕度范围内时，产品可以保证正常的运行状态；当试验应力水平超出工作应力裕度后，产品将部分或完全丧失应有的功能和性能。因此，在进行加速试验时，须保证加速应力水平小于产品的工作应力极限，在工作应力裕度范围内设定试验应力量值。产品的应力极限如图2所示。确定产品的应力极限可以通过步进应力试验得到，步进应力试验包括高/低温步进试验、振动步进试验和综合应力步进试验。

图2 产品的应力极限 Fig.2 Product stress limit

2 加速因子计算方法

2.1 元器件性能退化模型

2.1.1 阿伦纽斯（Arrhenius）模型

阿伦尼斯模型可以实现剖面各温度条件的时间比例转化：

式中：T1为基准温度，K；T2为需要折算的温度，K；t1是温度T2、持续时间t2的条件折算为基准温度T1后的持续时间；k为波尔兹曼常数，k=8.617×10–5。

根据式（1），将产品适用的可靠性试验剖面中的0 ℃以上温度时间（不含温变）折算至基准温度，得到单个循环剖面中折算后的时间tFN；对加速试验剖面中的正温时间（不含温变）折算至基准温度下的时间，得到单个循环剖面中折算后的时间为tFA，公式为：

式中：tFA为可靠性加速试验剖面折算至单个循环基准温度的时间；tFN为可靠性试验剖面折算至单个循环基准温度的时间；tA为可靠性加速试验条件单个循环时间；tN为可靠性试验剖面单个循环时间。

2.1.2 幂律模型

在加速试验中，除了温度应力以外，还大量应用了机械应力和电应力。物理上的许多实验数据证实，产品在机械应力与电应力作用下的反应速度与应力的关系常常满足幂律模型：

式中：K为反应速度；A和α为常数；S表示应力水平。

幂律模型表明，产品性能指标值的反应速度是应力的幂函数。对式（3）两边取对数，可得线性化（对lnS）的幂律模型：

其中，a=lnA，b=α。幂律模型适用于如机械疲劳、机械磨损、电压击穿、绝缘击穿等失效机理场合，表征产品寿命特征的逆幂律模型在机械产品和电工产品的加速寿命试验中应用广泛。

2.1.3 艾林（Eyring）模型

对于除温度以外还包含其他应力S的普遍情况，反应速度（速度）与应力的关系可用广义Eyring模型描述：

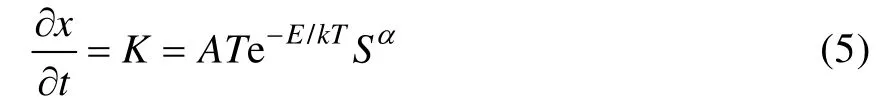
如果T变动范围较窄，上述模型即可变为热应力

变动范围不太大情况下的Eyring模型，即：

式中：A、E、α都是待定常数；k表示Boltzman常数；T为热力学温度；S表示温度以外的其他应力。

对式（6）两边取对数，可得线性化的Eyring模型：

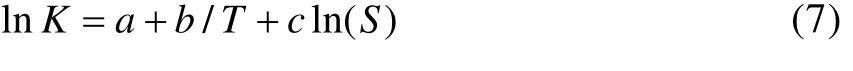
其中，a=lnA，b=－E/k，c=α。

就一般情况而言，如果引入性能指标值或量x的函数φ，则其与反应速度、速度的关系可以写为：

设t=0时，，则t时刻的量为:

在获得反应速度或速度的值后，即可得到产品的轨迹方程。从式（9）可以看出，量取决于，要使产品失效，增大速度或试验时间均可。增大应力（即增大速度K，进行加速试验）的结果与增加试验时间t是等价的。

2.2 互联模型

2.2.1 温度交变加速因子

1）通过可靠性仿真试验，得到产品在正常条件下热疲劳失效的前10个潜在薄弱点，假定其首发故障循环数分别为NT1,NT2,…,NT10。

2）在初步设定的加速条件下进行迭代的可靠性仿真试验，得到上面10个潜在薄弱点的首发故障循环数分别为NT′1,NT′2,…,NT′10。

3）将第i个潜在故障点在正常条件和加速条件下的首发故障循环数相除，得到第i个故障点的加速因子τVi，即

4）将10个潜在故障点的加速因子进行算术平均，即为产品的温度加速因子

2.2.2 振动加速因子

1）通过可靠性仿真试验得到产品在正常条件下振动疲劳失效的前10个潜在薄弱点，假定其首发故障时间分别为tV1,tV2,…,tV10。

2）在初步设定的加速条件下进行迭代的可靠性仿真试验，得到上面10个潜在薄弱点的首发故障时间分别为

3）将第i个潜在故障点在正常条件和加速条件下的首发故障时间相除，得到第i个故障点的加速因子τVi，即

4）将10个潜在故障点的加速因子进行算术平均，即为产品的振动加速因子

2.3 加权加速因子

最终加速因子计算方法见式（10）。

式中：Au为互联模型加速因子；AF为元器件退化模型加速因子；k1为互联模型权重；k2为元器件退化模型权重，k1+k2=1。

3 试验结果评估方法

对于定时截尾方案，当作出接收判决时，按式（11）对受试产品的平均故障间隔时间（MTBF）单侧置信下限进行评估：

式中：θL为MTBF的单侧置信下限；τ为加速因子；T为可靠性加速试验的实际试验时间；c为置信度；r为试验中出现的责任故障数。

对于序贯截尾试验的试验结果评估，由于其计算比较复杂，通常采用直接查表的方式进行，具体可见GJB 899A中的附录A。

4 加速试验条件及时间的确定流程

首先根据相关试验结果（仿真、强化、摸底、试飞）确定受试产品的敏感应力。当敏感应力为温度交变，或温度交变、振动均为敏感应力时，按照图3流程确定可靠性加速试验方案。

图3 温度敏感产品的可靠性加速试验方案制定流程 Fig.3 Reliability acceleration test scheme for temperature sensitive products

1）根据可靠性强化试验得出的工作应力极限，初步制定可靠性加速试验的温度应力条件，温度范围一般取可靠性强化试验得出的工作应力极限低温+ (10～20 ℃)、高温–(10～20 ℃)。

2）以可靠性试验剖面的温度条件和常规试验时间对应的试验循环数为输入，通过可靠性仿真试验得出的加速模型，计算在1）中给出温度条件下的等效试验时间。

3）确认等效试验时间是否合理，如果不合理，调整1）中的温度应力条件，重新进行计算，直至得到合适的等效试验时间。

4）以可靠性试验剖面的振动条件和常规试验时间为输入，通过可靠性仿真试验得出的加速模型，计算在3）中得出的等效试验时间内的振动量值。如果该振动量值超过产品技术协议或规范中规定的功能振动量值，则调整1）中的温度应力条件，重新进行计算，直至等效试验时间在合理区间内内，且振动量值不大于功能振动量值。

5）综合1）中最终确认的温度应力、电应力（在低温保持结束前进行通电，高温保持结束时断电）和4）中得出的振动应力（除低温不通电阶段外连续施加振动），即为可靠性加速试验综合环境条件，得出的等效试验时间即为可靠性加速试验时间。

当敏感应力为振动应力时，按照图4流程确定可靠性加速试验方案。

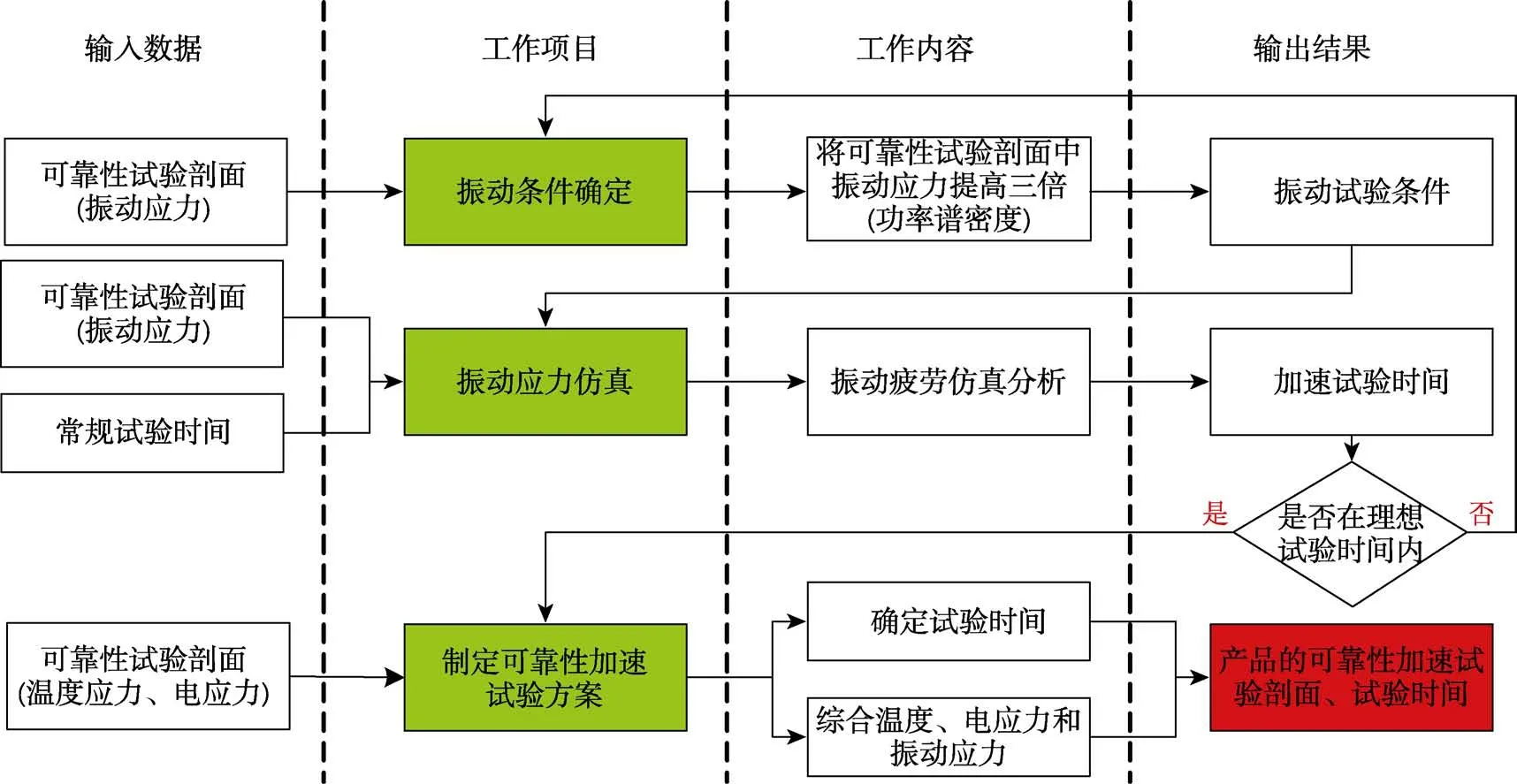
图4 振动敏感产品的可靠性加速试验方案制定流程 Fig.4 Reliability acceleration test scheme for vibration sensitive products

1）根据以往振动故障物理结果，初步将可靠性试验剖面中的振动功率谱密度提高3倍，作为可靠性加速试验的振动应力条件。

2）以可靠性试验剖面的振动条件和常规试验时间为输入，通过可靠性仿真试验得出的加速模型，计算在1）中得出的可靠性加速试验振动应力条件下的等效试验时间。

3）确认等效试验时间是否合理，如果不合理，调整1）中的振动应力条件（振动功率谱密度提高倍 数），重新进行计算，直至得到合适的等效试验时间。4）综合1）中最终确认的振动应力和可靠性试验剖面中的温度和电应力，即为可靠性加速试验综合环境条件，3）中得出的等效试验时间即为可靠性加速试验时间。

5 案例

5.1 可靠性加速试验方案设计流程

在进行可靠性加速试验方案设计[13-16]时，需要开展分析工作和权衡决策工作。分析工作主要包括产品故障物理分析[17-18]、产品主要故障机理确定、加速试验条件确定和加速模型或加速因子确定[19-25]。权衡决策工作主要包括试验截尾方案的确定、受试产品数量和要求、试验结果评估方法的选择等。可靠性加速试验方案设计基本流程如图5所示。

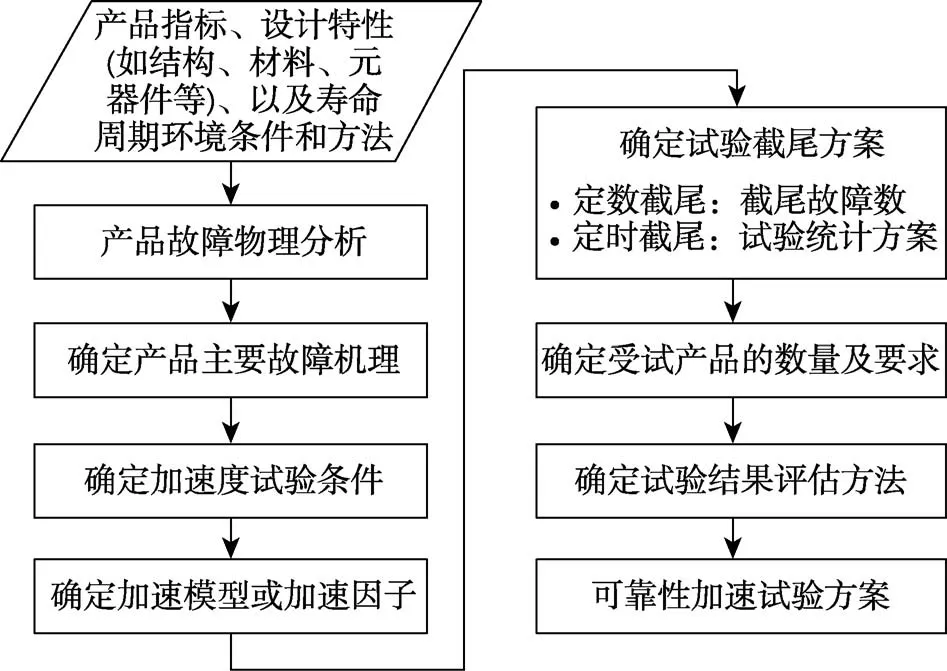
图5 可靠性加速试验方案设计流程 Fig.5 Reliability acceleration test scheme design process

5.2 加速因子确定

某型产品安装在飞机设备舱，其可靠性试验剖面如图6所示。

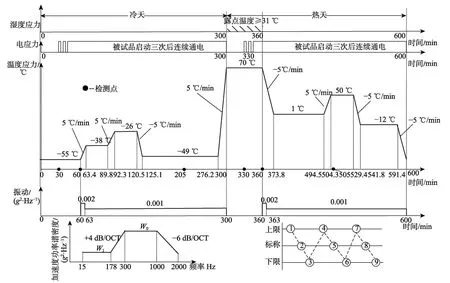
图6 某型产品可靠性试验剖面 Fig.6 Reliability test profile of a product

根据强化试验得到的极限工作应力（低温为–75 ℃、高温为110 ℃），初步确定温度循环条件，见表1。

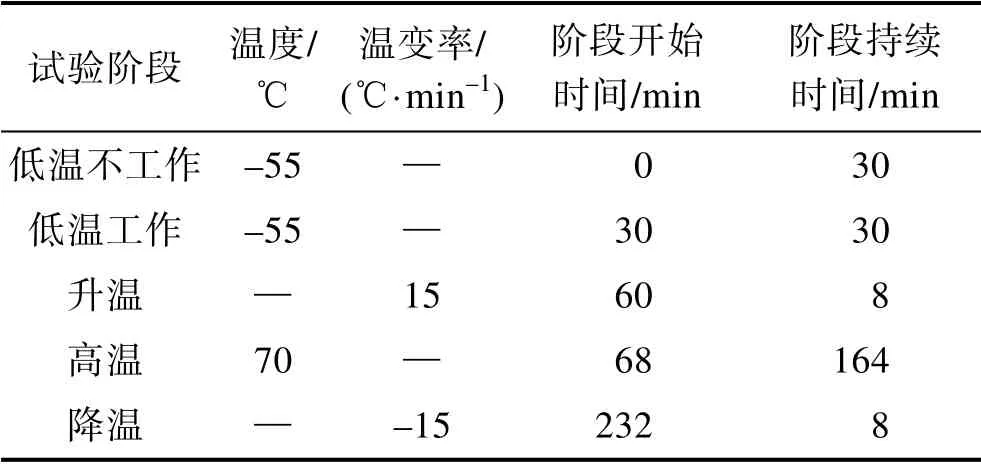
表1 某型产品初步可靠性加速试验温度应力条件 Tab.1 Preliminary reliability acceleration test temperature stress conditions for a product

按照HB 20091的要求，建立可靠性仿真模型，并进行应力损伤分析，得到产品的故障信息矩阵。分别以可靠性试验剖面温度应力条件相关特征值和确定的初步可靠性加速试验温度应力条件相关特征值为输入，按照HB 20092的要求进行可靠性仿真评估，得到产品前20个薄弱环节在可靠性试验剖面和初步可靠性加速试验温度应力条件下对应的首次故障时间以及各薄弱环节的加速因子，见表2。

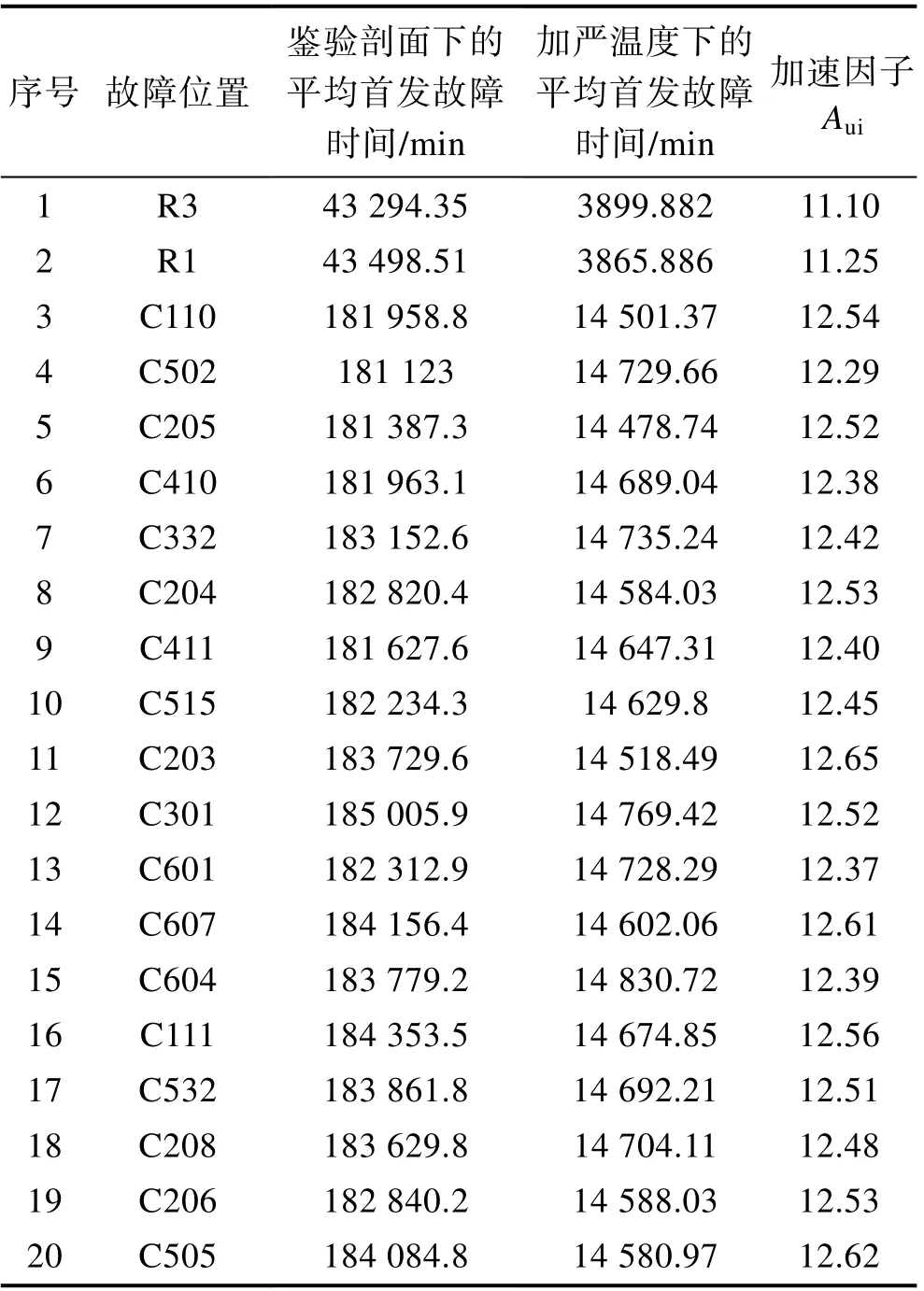
表2 某型产品前20个热疲劳薄弱环节 Tab.2 The top 20 hot fatigue of a product

将以上20个薄弱环节点的加速因子进行算术平均，得到产品的互联模型加速因子Au：

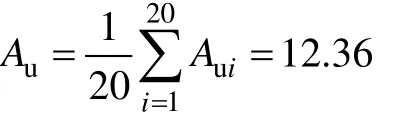
可靠性试验剖面中0 ℃以上的温度段折算到基准温度（取值为21 ℃）后的单个循环剖面时间tFN约为5564 min。初步可靠性加速试验温度应力条件中0 ℃以上的温度段折算到基准温度后的单个循环剖面时间tFA约为14 051 min。按照式（2）计算性能退化模型加速因子为6.3。由于该产品为元器件国产化产品，比例系数a取0.2（根据产品的特点确定，如果元器件质量和成熟度较低，则a的取值一般较大，反之亦然），按照式（10）计算加速因子为7.5。

5.3 可靠性加速试验时间和条件确定

该产品的平均故障间隔时间（MTBF）最低可接受值为3000 h，选择GJB 899A—2009[21]中方案30-1，则常规应力下的试验时间为3600 h，可靠性加速试验时间为480 h。该时间满足进度和经费要求，不需调整。

确定可靠性加速试验条件如下。

1）温度应力。可靠性加速试验条件的温度应力为5.1节中温度应力条件。

2）湿度应力。在高温阶段开始30 min后施加，持续时间1 h，量值同可靠性试验剖面，即露点温度不小于31 ℃。

3）电应力。低温段前30 min不加电，在通断电 3次后，连续加电，量值同可靠性试验剖面。

4）振动应力。最大振动的量级同可靠性试验剖面（0.002g2/Hz），在3～33 min、98～101 min施加。加权振动在33～98 min、101～240 min施加，加权振动的量值计算：将3600 h常规试验中的振动折合至0.002g2/Hz量级对应的时间（振动常数因子b的值由材料的疲劳强度指数取值确定。引线和焊点的疲劳强度指数一般为6.4，振动常数因子即为3.2），T1= 85 320 min，T折=11 444 min。计算加速试验中累计同等振动效果所需的量级，T1=24 480 min，T2= 10 724 min，W1=0.002(T2/T1)1/3.2≈0.001 545g2/Hz。

综上所述，可靠性加速试验条件如图7所示。

图7 某型产品可靠性加速试验剖面 Fig.7 Reliability acceleration test profile of a product

5.4 试验结果

本次可靠性加速试验被试品数量为1件，试验共进行480 h，受试产品未出现故障，按照公式（11）进行评估。T取480 h，加速因子 totalA为7.5，责任故障数r为0，置信度c取70%，计算得θ≥3000 h。

因此，在480 h的加速试验（等效3600 h正常试验时间）结束后，在70%置信度下，受试产品的平均故障间隔时间（MTBF）单侧置信下限为3000 h。

在该案例中，通过采用基于故障物理和数理统计相结合的可靠性加速试验方案设计方法，基于仿真分析和统计模型的建立，通过适当加大试验应力，将原本需要开展3600 h的可靠性试验等效为480 h的加速可靠性试验，大大缩短了试验周期。

6 结语

该方法综合考虑了加速因子计算的两种模型（基于故障物理的互联模型和基于数理统计的元器件退化模型），建立了综合互联模型和元器件退化模型的加权加速因子计算模型，形成了电子设备基于故障物理和数理统计相结合的可靠性加速试验方案设计方法，解决了高可靠性、小样本产品的可靠性加速试验方案设计问题。经案例验证，该方法能够满足当前可靠性要求高、进度紧、受试样品有限的武器装备研制的需求。