垂直塔座椅弹射试验永磁涡流制动可行性分析

李承觊，张德远

（1.中电科航空电子有限公司，成都 611731； 2.北京航空航天大学 机械工程及其自动化学院，北京 100191）

弹射座椅为飞行员专用座椅，在飞机失控状态下，为保护飞行员的生命安全，而将飞行员弹离飞行器，并使其安全着陆的航空救生设备[1]。飞机座椅弹射试验已成为飞机功能试验必不可少的部分，具体试验表现形式为水平姿态的火箭撬滑轨试验和不利姿态的垂直塔轨道滑车自由落体坠落试验[2]。传统的垂直塔缓冲防坠系统采用的是固定在垂直塔上的摩擦片与滑车的车轮刚性摩擦减速[3]，抱死滑车后，再进行滑车的吊装拆卸。试验前后的准备时间较长，效率低，影响了整体的进度。

涡流制动采用永磁涡流制动或电磁涡流制动[4]，高速制动性能好。朱先福等人[5]进行了涡流制动的制动力分析与计算。童昕宏等人[6]进行了永磁涡流模拟仿真软件设计。永磁涡流制动由于具备高速制动性能好、不引入外部能量、系统简单等优点，同时在永磁制动新材料的研发上不断有新的突破，吸引了国内外学者广泛的重视[7]。

目前，永磁涡流制动系统一般应用于游乐场升降娱乐设施或高速轨道车辆上，鲜有将其应用于垂直塔座椅弹射试验的报道。文中提出将永磁涡流系统用于垂直塔座椅弹射试验中的制动系统，由于不需要车轮钢性摩擦和吊装拆卸，可大大缩短试验周期，提高试验效率。

1 永磁涡流制动器及其制动原理

永磁制动器结构如图1所示，包括安装在滑车上的动子板，固定在塔体的静子板，其中，滑车动子板上布置了3个磁场，分别包括一块相对设置的S极和N极板，安装在塔体静子板上的3个导体（如不锈钢、铜镍合金、7075铝合金）分别插入动子板上布置的3个磁场中。缓冲过程中，安装在滑车上的动子板（永磁体）与固定在塔体的静子板（导体板）相对运动形成电磁拉力，对滑车的自由落体形成反向制动，即该系统实质上是一种能量转换装置。在试验过程中，滑车的重力势能转换为动能，再通过永磁涡流制动，将动能转换成磁能和热能[8]，从而达到制动的效果。由此产生的热量，通过自然风冷进行热交换。

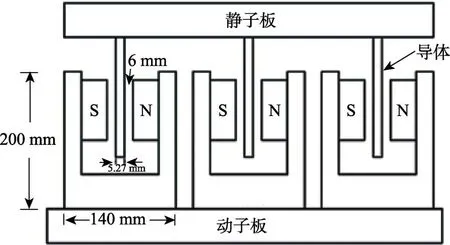
图1 永磁涡流制动系统原理 Fig.1 Principle of permanent magnet eddy current braking system

2 滑车试验系统及试验制动要求

滑车试验系统主要包括垂直塔、滑车轨道、滑车、缓冲系统、制动系统。滑车有2种类型，3、5 t各1台，滑车轨道长度为120 m。试验要求为3 t滑车下滑时，以最大速度30 m/s实施制动减速；5 t滑车下滑时，以最大速度60 m/s实施制动减速，制动过程中过载不大于6 G，制动距离不大于40 m。

垂直塔塔体有凹槽，槽内竖直方向铺有4根轨道，滑车可沿轨道作自由落体运动。永磁涡流制动系统包含动子板和静子板，动子板安装在滑车车座下，选用300 J/m3的钕铁硼（N45或45M）[9]。静子板固定在基座墩子，基座墩子与塔体凹槽内的地脚螺栓固定在一起，作为固定静子板的基础。

3 模拟分析

3.1 磁感强度计算

涡流产生的磁场属于时变场，是随时间变化而变化的[10]。根据麦克斯韦方程计算磁感应强度B，见式（1）。

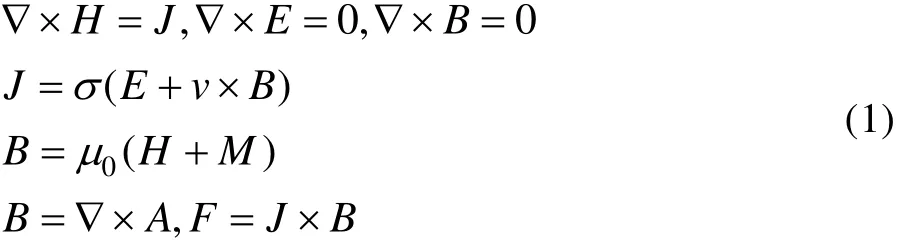
在固定磁体的磁轨和气隙，矢量磁势A分布见式（2）。

磁化强度为M，永磁体区域磁势A分布见式（3），μ为永磁体磁导。

感应板区域矢量磁势A分布见式（4）。

用若干个面积为1平方厘米的小正方形摆拼不同的图形，通过拼组图形使学生体会：尽管所拼图形的形状各不相同，但图形的面积均相等。学生在操作中感受面积守恒。

式中：μr为感应板相对磁导率；μo为气隙磁导；v为滑车速度；σ为电导率。

为了计算方便，将间断的永磁体等效成连续的永磁体面，通过傅立叶变换得到等效后的磁化强度M，分别为n次傅里叶变换在水平和垂直方向的幅值[10]。

由式（1）—（5）得出感应板中的磁感应强度分布，见式（6）。

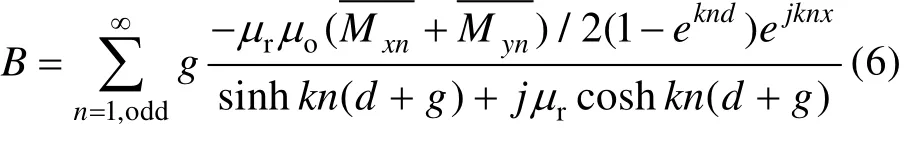
式中：d为永磁体厚度；g为气隙。

3.2 制动力计算

由感应板的磁感应强度和麦克斯韦的应力张量法[11]，得到总制动力计算公式，见式（7）。

式中：r=1,3,5,…，取前五项，r=1,3,5,7,9；f为级距；p为极对数；lp为初级长度，lp=2pf；w为初级宽度；T为占空比，T=lm/f（lm为永磁体长度）；e为总气隙；v为次级板（滑车）的速度。各参数的具体取值见表1。

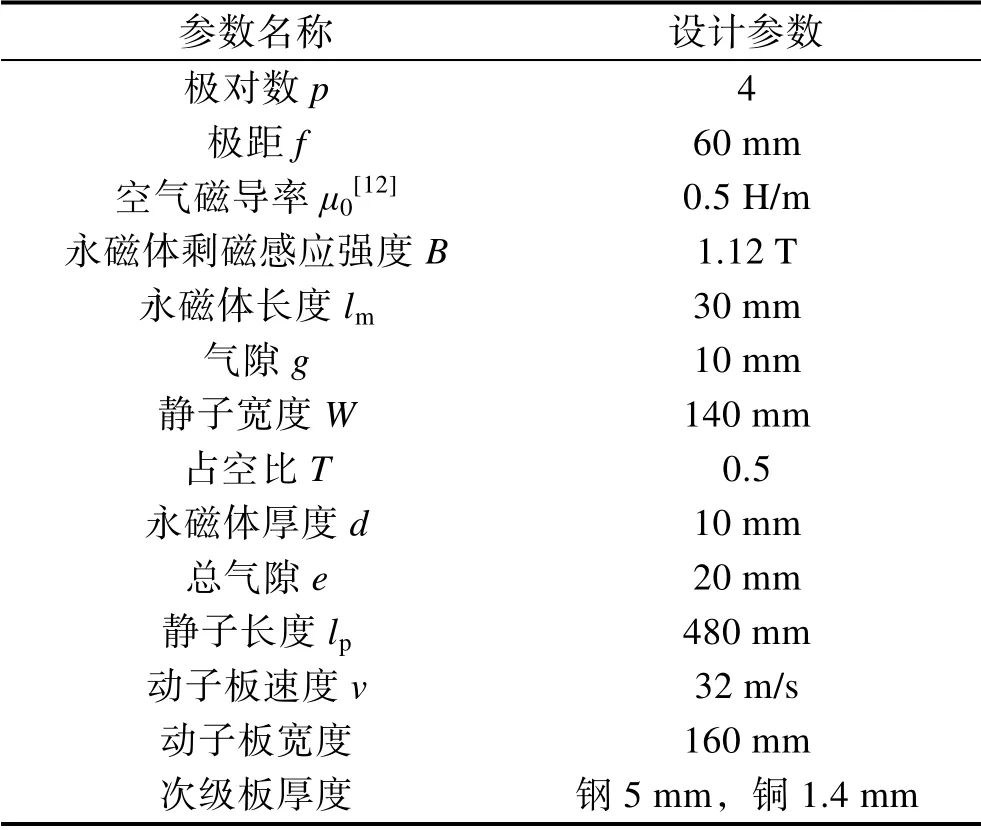
表1 设计参数 Tab.1 Design parameters

3.3 仿真计算

通过电磁场有限元仿真计算，针对3 t滑车下滑最大速度为30 m/s时实施制动减速。模拟了制动距离30 m、最高制动速度30 m/s的关系曲线，如图2所示。

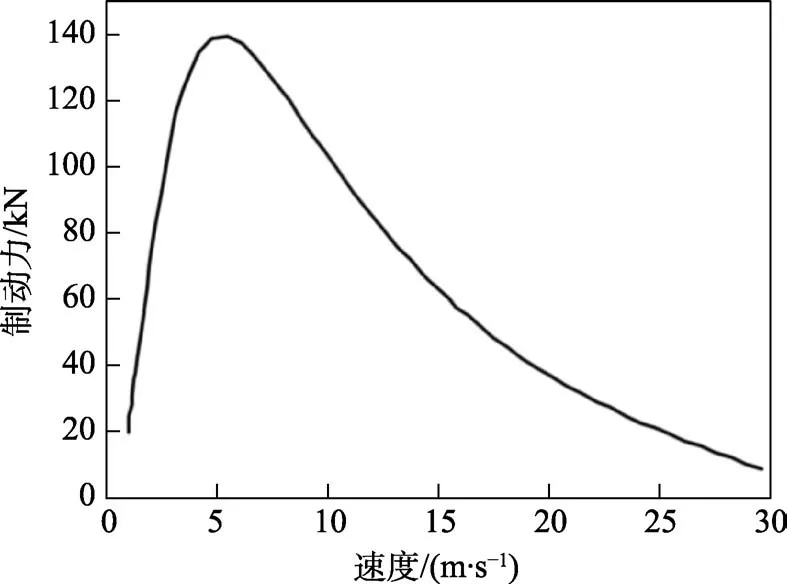
图2 30 m距离制动力与速度的关系曲线 Fig.2 Relationship between braking force and speed at the braking distance of 30 m

在30 m，制动速度为30 m/s的情况下，随着滑车速度的持续减小，电磁制动力先增加、后减小，在6 m/s时达到最大。这是由于滑车速度减小，气隙中磁力线的倾斜度不断增加，增大了制动力；随着滑车速度持续减小，制动力增大到最大峰值后，同动子板交接的磁力线密度增大过密，漏磁也不断加大，此时制动力开始减小[13]。最后电磁拉力在速度达到2 m/s时，不再减小，完成了制动缓冲过程。由图3和图4得出，制动速度、制动距离与制动时间参数的关系是制动速度随着制动时间的增加而持续减小，最终匀速运动，制动距离随着制动时间的增加而持续增加，最终停留在35 m处。能够满足试验总体制动距离不超过40 m的要求。

图3 30 m距离制动速度与时间曲线 Fig.3 Relationship between braking speed and time at the braking distance of 30 m

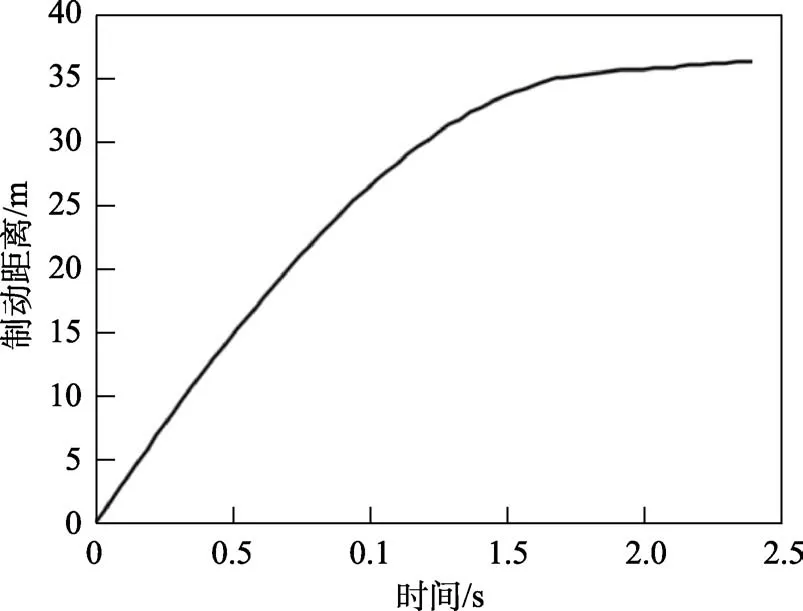
图4 30 m/s制动速度下距离制动距离与时间曲线 Fig.4 Relationship curve between braking distance and time at the braking speed of 30 m/s

4 系统优化

为研究静子板感应材料对制动系统制动效果的影响，分别研究了不同材料作为静子板感应材料的情况下制动系统的制动效果。一般常用的导体是不锈钢、铜镍合金和7075铝合金等，分别选取同样高度的不锈钢、铜镍合金和7075铝合金作为永磁涡流制动静子板的感应板材料。针对5 t滑车下滑最大速度为60 m/s实施制动减速的试验工况，通过仿真计算来模拟极限工况下的制动力随滑车运动速度变化的特征曲线，如图5所示。

图5 不同材料的制动力与滑车速度关系曲线 Fig.5 Relationship between braking force and pulley speed of different materials

当静子感应板采用不锈钢时，随着速度变小，其制动力平稳变化。这是由于不锈钢的电导率小，磁导率大，产生涡流以及制动力较平稳，同时不锈钢电导率比其他材料小，所以峰值制动力相对较小。在速度为55 m/s时，产生最大拉力。总体制动速度变化过程相对平稳。

当静子板感应板采用铜镍合金或铝合金7075时，由于二者的电导率大，磁导率小，永磁体产生的绝大部分磁通会选择相对磁阻较小的路径，而不与静子板的铜板或铝合金板交链而形成漏磁[14]。在高速时，产生涡流的磁通较少，所以制动力较小。随着速度的持续减小，产生涡流的磁通较多，再加上铜镍合金或铝合金的电导率大，这样产生的峰值制动力较大。最终，采用铜镍合金和铝合金7075作为动子感应板时，分别在速度为25 m/s和12 m/s产生最大制动力，之后制动力平稳减小。

动子板随滑车自由落体，经过静子板区域，因制动过程产生涡流，在高电导率的感应板中涌动，而磁通通过高磁导率的感应板形成闭合回路。对于不同材料的静止板感应材料，由于电阻率的差别（钢的电阻率高于铝，铝高于铜），导致涡流制动的力学性能不同[15]。从图5可以看出，同一工况下能够产生的峰值制动力均在450 kN左右，但达到峰值的制动速度不一样（不锈钢为65 m/s，铜镍合金为25 m/s，铝为12 m/s）。因此，对于速度区间较低的制动，采用铜镍合金或者铝合金会比不锈钢的制动效果更好一些；而对于速度较高的制动中，不锈钢的制动效果较好一些。

基于此，文中对永磁制动系统的静子板材料进行优化：高速制动段采用不锈钢，中速制动段采用铜镍合金，低速制动段采用铝合金。

5 结论

文中提出了采用永磁涡流制动的方法来实现试验滑车的制动，通过对磁场的模拟，制动力的计算，模拟分析了永磁涡流制动过程，得出了30 m制动距离下制动力与速度、制动距离与时间的关系，验证了永磁涡流制动系统能够满足垂直塔座椅弹射试验对制动系统的要求（总体制动距离不超过40 m）。同时，模拟分析了静子感应板不同材料对制动效果的影响，并基于研究结果提出了对永磁制动系统静子板的材料进行优化的方案。

尽管永磁涡流系统能够满足制动试验的要求，但目前永磁涡流制动仍存在两个弊端：轨道温升问题和制动特性不易调节。具体体现在，根据能量守恒定律，由涡流制动产生的制动力沿着竖直轨道所做的电磁拉力功与该段轨道势能减少、动能减小以及由制动导致增加的热能是恒定的，因此制动段制动系统的温升是必然的[16]。同时，永磁涡流制动系统的永磁材料与其他参数对于系统制动具有唯一性，因此不能兼顾其他制动要求[17]，永磁体涡流制动最终不会将滑车停止。因此，需要外加辅助系统进行停止制动。因此，如何有效解决以上几个问题将是今后该领域进一步研究的方向。