基于非线性PID的列车速度控制
2021-11-03陈旭杨振波
陈旭 杨振波


DOI:10.19850/j.cnki.2096-4706.2021.08.011
摘 要:列车自动驾驶系统能提高轨道交通的效率,而它的主要功能是对列车速度的自动控制。与其他的一些控制对象不同,列车速度的自动控制除了要控制好速度以外,还需要考虑到乘客的舒适感。为此,文章设计了一种基于非线性PID原理的控制器,并通过MATLAB软件的Simulink模块进行了仿真。仿真结果表明,该控制器能在保证乘客舒适性的情况下有效跟踪目标速度信号。
关键词:PID控制;非线性PID控制;列车自动驾驶系统
中图分类号:TP273 文獻标识码:A 文章编号:2096-4706(2021)08-0038-04
Train Speed Control Based on Nonlinear PID
CHEN Xu,YANG Zhenbo
(The College of Information Engineering,Guangzhou Vocational and Technical University of Science and Technology, Guangzhou 510550,China)
Abstract:Automatic train operation can improve the efficiency of rail transit,and its main function is automatic control of train speed. Different from some other control objects,the automatic control of train speed not only needs to control the speed,but also needs to take the comfort of passengers into account. Therefore,a controller based on nonlinear PID principle is designed in this paper,and the simulation is carried out through Simulink module of MATLAB software. The simulation results show that the controller can effectively track the target speed signal under the condition of ensuring the comfort of passengers.
Keywords:PID control;nonlinear PID control;automatic train operation
0 引 言
作为列车自动驾驶系统中最主要的功能,对速度控制的效果关系到列车系统运行性能的好坏。一个好的列车速度控制策略除了要达成速度控制本身的快速性、精确性、以及稳定性以外,还需要顾及到列车上的乘客的舒适性。为满足上述指标,常见的做法是先根据速度和对舒适性的要求生成一条平滑的目标曲线,再令控制系统以正常的方式去跟踪速度的目标曲线[1]。这种方式的控制策略对控制器的要求主要体现在控制超调量上,因为对舒适性的考虑基本由对速度的目标曲线的规划去解决。而与之不同的是,不依赖于对目标速度曲线的规划,本文所设计的控制器即使是在阶跃信号输入的情况下也能满足控制系统对消除速度误差以及保证舒适性的要求。
1 控制对象分析
用于评价列车速度控制的效果的指标有很多,如,速度控制与位置控制的“快”“准”“稳”,又如能耗还有舒适性等[1]。其中,本文以速度的控制以及舒适性的提升为控制器设计的目标。而舒适性的指标又包括了加速度和冲击率。加速度是速度的微分,冲击率是加速度的微分。根据文献[2],为了保证乘客的舒适,要求控制系统输出的加速度不高于1.2 m/s2,并且冲击率不高于0.4 m/s3。列车有3种不同的运行模式,分别是牵引模式、惰行模式以及制动模式[3]。为保证列车平稳运行,要求牵引模式与制动模式之间不能直接切换而必须经过惰行模式的过渡。而且不同模式之间的切换不能过于频繁,过渡的模式必须维持一定的时间后才能被切换到下一个模式。因此,本文所设计的控制器在对速度进行控制时,设定列车只工作在牵引模式下,其控制器最低输出的幅值为0而非负值,再设控制器最大输出的幅值为25。
为了方便对列车的速度控制系统进行分析,在控制系统建模时将列车视为一个质点,有以下传递函数[3]:
式中,s为拉普拉斯域的复变量。由式1可见,在对列车速度的控制系统进行分析时,控制对象可被简化为一个线性系统,并可以由一个二阶的传递函数进行描述。
2 PID控制器
PID控制器由P、I、D这3种控制器线性组合而成。P控制器即比例控制器,它输出与误差成比例的控制信号以使响应曲线逼近输入曲线;I控制器即积分控制器,它通过对系统输出的误差信号进行积分从而可以提供消除误差的能力;D控制器即微分控制器,它通过与系统曲线变化趋势相反的输出去增大系统的阻尼以减少输出曲线的超调量从而提高系统的稳定性。P控制器与D控制器本身并不具备消除静态误差的能力,因为绝大多数被控对象都需要一个来自控制器的非零的输出来维持自身的稳态,而在系统进入稳态、误差及其变化率都为零时P控制器与D控制器的输出都为零。在3个子控制器中只有I控制器能在系统进入稳态时其输出量不为零,I控制器消除误差的过程从某种程度上而言就是寻找使控制系统达到稳态的终值的过程。
PID控制器无论是其组成的结构还是其参数的调节都比较简单,同时还具备能消除静态误差、弱模型依赖的特性,但是,这样的控制器也存在着一些不足,例如,在提高系统的响应速度与抑制系统的超调量这两个指标之间的矛盾[4,5]。
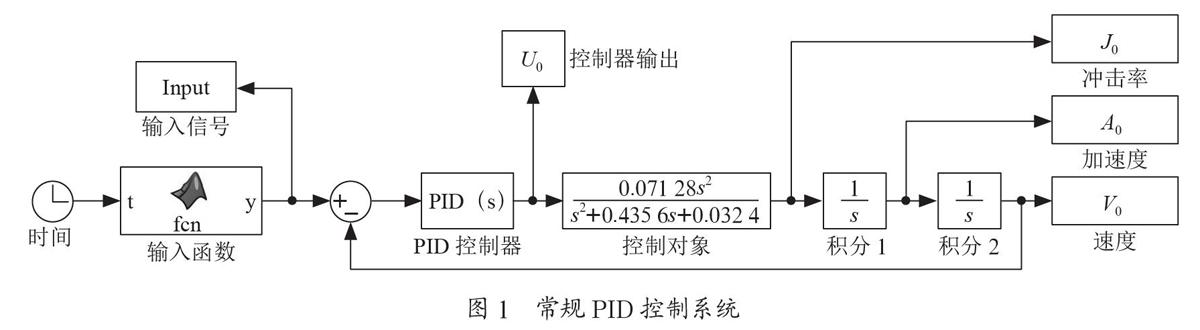
作为用于参照比对的系统,本文用到的常规PID控制系统为连续时间系统,并且对控制器的输出不作幅值上的限制,其参数的选取参照文献[3],分别为:KP=15.5,KI= 13.4,KD=13.1。采用常规PID算法的列车速度控制系统的Simulink系统框图如图1所示。
为提高在Simulink中建模的系统输出曲线的精度,应尽可能避免出现纯微分环节。在本文中对加速度与冲击率的测量所需的微分环节可通过调整传递函数的阶数后用积分环节取代。
3 非线性PID控制器
为了减弱常规PID控制算法的负面效果,对其参数进行非线性化改造,于是有了非线性PID控制器。对于P控制器而言,参数调大了就会增加超调量,参数调小了就会降低逼近目标曲线的速度,所以,一般而言,当系统的误差较大时,采用较大的参数,而误差较小时则采用较小的参数;对于I控制器而言,参数大了会加大超调量并引起系统振荡,参数小了会延长消除静态误差的时间,因此,通常的做法是较大的误差对应较小的参数,较小的误差对应较大的参数;为了在系统误差小时增大系统的阻尼,而在系统误差大时加快系统响应的速度,D控制器的调参策略与P控制器相反[6]。
通过对文献[7]的参考、分析控制对象的特性以及仿真实验的比较,引入sech函數,采用以下结构的非线性P、I、D模型,它们的输出分别为:
P(e)=sign·a1·(1-sech(a2·e)) (2)
I=I+T·a3·e·sech(a4·e) (3)
D(e)=a5·Fs·?e·sech(a6·e) (4)
式中,a1~a6是常数,T是控制器输出刷新的采样时间,Fs是传感器的采样频率。其中的非线性P控制器在系统误差超出一定的值后迅速逼近最大输出,I控制器与D控制器则在误差较小时有较大的系数,当误差较大时对应的系数则较小。根据列车的运行情况与控制器的输出情况,可以得知I控制器的终值既不可能低于0也不可能高于25,因此设定I控制器值的范围为0~25,以提高响应速度并降低超调量。
4 保证舒适性的机制
无论是常规的PID控制器、上述的非线性PID控制器还是其它文献里的控制器,对舒适性的考虑都依靠事先设计好一条满足加速度与冲击率要求的平滑的目标曲线,再令控制器以尽可能小的超调量去跟踪设计好的目标曲线,而没有考虑当输入信号为任意信号(如阶跃信号)时如何限制好加速度与冲击率的问题。在列车运行的过程中,有可能会出现各种预料以外的情况以至于未必总能按预定的目标速度曲线行驶(如临时停车),所以,控制器本身对加速度与冲击率的限制也是有意义的。
4.1 对加速度的限制
为了使控制系统能够在任意目标速度信号的输入下都能把列车的加速度限制在1.2 m/s2以下,参考在文献[8]中模仿免疫系统中抗体浓度调节的免疫调节器的结构与原理,引入限制加速度的机制。
根据免疫调节原理,当机体的抗原浓度高而抗体浓度低时,免疫系统会促进淋巴B细胞分泌抗体以尽快消灭抗原。而当抗原浓度低而抗体浓度高时,免疫系统会抑制抗体的生成以避免抗体浓度过高,因为过高的抗体浓度可能会引起炎症或过敏。文献[8]中的免疫调节器本质上是个不具备静差消除能力的非线性PD控制器,其控制器输出如式(5)所示。
UNPD=K(1-k·f(?U))·e (5)
其中,K和k均为比例系数,K大于0,k大于0小于1,f( )为与控制器输出的变化率正相关的非线性函数。针对限制加速度的问题,在本文中,将原来的机制调整为式(6)与式(7)的模式:
其中,U为控制器的输出,U0为未加加速度限制机制前控制器原本的输出,A为加速度,当A大于1.2时,采用式(6),当A小于-1.2时,采用式(7),b1为一个大于0但小于1.2的常数,b2的取值范围为0~1。系统输出的加速度越大,该机制对控制器总输出的抑制或往反方向进行调整的幅度也越大。
4.2 对冲击率的限制
控制对象的速度的传递函数的二阶微分即其冲击率的传递函数。由初值定理及其阶跃响应可知,在一个很短的时间内,控制器输出每增加1,控制对象相应地会产生0.071 28的冲击率,但其冲击率会随着时间的推移而衰减。由此可见,只要能够根据冲击率实时的裕量限制控制器输出量的变化幅度,就可以令冲击率不超出限定的范围。
5 仿真分析
采用非线性PID算法的列车速度控制系统的Simulink系统框图如图2所示,该系统为离散时间系统。
其中,控制器输出刷新的频率为100 Hz,传感器采样的频率为200 Hz,其延时为一个采样周期,控制量输出幅值的取值范围为0~25,控制器的内部参数a1=25,a2=22.5,a3=30,a4=3,a5=55,a6=1,b1=0.6,b2=0.75。
参照文献[3]中的部分仿真条件,目标速度从第5秒由0以斜率为0.75的加速度增加至15,常规PID控制器与非线性PID控制器的控制效果如图3所示。
由两种控制系统所输出的响应曲线的对比可知,虽然非线性PID控制器在跟踪平缓曲线信号时会为系统带来更大的超调量,但这里面有限制冲击率的考虑,并且,在超调后非线性PID依然能使系统以更快的速度达到稳定状态。
测试控制器自身对加速度与冲击率的限制的能力,采用阶跃信号为输入,目标速度从第5秒由0变成15,常规PID与非线性PID的控制效果如图4所示。
由系统仿真的结果可见,针对舒适性进行改良后的非线性PID控制器能令系统在保证加速度与冲击率达标的情况下有效响应阶跃信号。
6 结 论
本文以列车的二阶线性简化模型为控制对象,基于非线性PID算法设计了一种控制器,并加入了限制加速度与冲击率的机制。根据仿真实验的结果,不论是输入平缓曲线还是阶跃信号,该非线性PID控制器都能快速的消除误差并使加速度与冲击率不超出规定的范围。
针对控制对象的特性,在设计控制器时,可考虑根据输入信号、建模误差、可能的干扰量进一步动态地调整I控制器的上限值与下限值,以减少不必要的振荡并且加快静差的最终消除。除了本文的设计外,要控制加速度与冲击率,还可以考虑设计速度、加速度、冲击率的3闭环系统,但相应地,控制系统的设计也会更加复杂。
参考文献:
[1] 唐涛,黄良骥.列车自动驾驶系统控制算法综述 [J].铁道学报,2003(2):98-102.
[2] 门进博,车军.城轨列车自动驾驶舒适性算法研究与仿真 [J].甘肃科技纵横,2021,50(4):21-24.
[3] 孟建軍,张宏强.基于改进灰色预测模糊PID控制的列车多目标优化研究 [J].铁道标准设计,2020,64(5):173-181.
[4] 连文博,刘伯鸿,李婉婉,等.基于自抗扰控制的高速列车自动驾驶速度控制 [J].铁道学报,2020,42(1):76-81.
[5] 韩京清.非线性PID控制器 [J].自动化学报,1994,20(4):487-490.
[6] 唐胜景,陈天悦,李震,等.基于感知模糊自适应蚁群算法的非线性PID控制设计 [J].计算机测量与控制,2016,24(11):91-94+99.
[7] 范政,赵虹.基于非线性PID的连续搅拌反应釜控制方法 [J].科学技术与工程,2021,21(7):2754-2759.
[8] 马向东.基于免疫原理的控制器研究与设计 [D].哈尔滨:哈尔滨工程大学,2009.
作者简介:陈旭(1992—),男,汉族,广东佛山人,助教,硕士,研究方向:电子电气相教学与科研;杨振波(1986—),男,汉族,广东河源人,讲师,高级技师,本科,研究方向:电子电气教学与科研。
收稿日期:2021-03-16
