面向储能应用的双向变换器分数阶建模研究
2021-11-03李娜


DOI:10.19850/j.cnki.2096-4706.2021.08.010
摘 要:对于目前储能系统中的双向BUCK-BOOST变换器,传统用的建模方法都是采用整数阶建模,而实际应用中电容电感都是分数阶的。因此基于分数阶微积分分别建立了充电和放电模式下的BUCK-BOOST变换器的模型,并且将所得的分数阶模型与传统的整数阶模型进行对比分析。表明该方法建立的模型能真实反映变换器的动力学行为,可以使以后的储能控制更加精确。
关键词:双向BUCK-BOOST变换器;分数阶微积分;整数阶模型
中图分类号:TM46 文献标识码:A 文章编号:2096-4706(2021)08-0034-05
Research on Fractional Order Modeling of Bidirectional Converter for
Energy Storage Application
LI Na
(Shandong Huayu University of Technology,Dezhou 253034,China)
Abstract:For the bidirectional BUCK-BOOST converter in the current energy storage system,the traditional modeling methods are all using the integer order modeling,while the capacitance and inductance in practical application are all of fractional order. Therefore,based on the fractional order calculus,the model of the BUCK-BOOST converter in charge and discharge mode are established respectively,and comparative analysis is made on the obtained fractional order model and the traditional integer order model. It shows that the model established by this method can truly reflect the dynamic behavior of the converter and make the energy storage control more accurate in the future.
Keywords:bidirectional BUCK-BOOST converter;fractional order calculus;integer order model
0 引 言
近年来,随着能源危机、环境污染等问题日益严重,能源问题成为制约整个国际社会发展的重要因素,如何高效利用能源成为当今社会的研究热点,越来越多的学者已开始关注光伏和燃料电池等新能源技术[1]。但由于新能源的发电效率受气候条件和天气变化的影响大,使得输出电能不连续、不稳定,因此就需要加入储能用的双向DC/DC变换器,使其在不同的工作情况下都能稳定工作[2,3]。本文采用的是双向BUCK-BOOST变换器[4,5]。
对于BUCK-BOOST变换器的控制,以往常采用传统的小信号模型进行控制[6-8],虽然该模型已经相当成熟,但是此建模的原理主要是将电路中的电感和电容是当作整数阶模型来描述的。而根据研究表明在实际上电容和电感均是分数阶的,因此必须建立其分数阶模型,这样才能更加准确地描述电感和电容的特性。
综上可以得出,运用整数阶模型不能够精确的模拟实际电容和电感的特性,导致BUCK-BOOST变换器的整数阶建模是不够准确的。因此,基于分数阶微积分来研究BUCK-BOOST变换器的建模是很有必要的。目前,也有不少文献对基于分数阶微积分的建模有所研究[9-11]。
1 儲能系统中双向BUCK-BOOST变换器模型
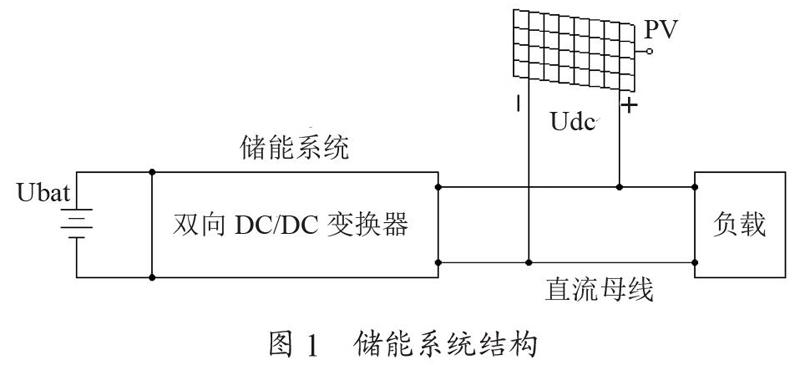
本文所选择的储能系统是基于直流母线的储能系统,系统结构如图1所示。由蓄电池和双向DC/DC组成的储能系统连接在直流母线上,当直流母线所提供的能量充足时,储能系统通过双向DC/DC变换器给蓄电池充电,实现电能的存储;当直流母线电能匮乏时,储能系统将蓄电池中所储存的能量经双向DC/DC变换器输送到直流母线上,保证系统持续、稳定工作。
双向DC/DC变换器的拓扑如图2所示。当直流母线给既给负载提供能量又给蓄电池充电时,即S1导通,S2关断,双向DC/DC工作在BUCK模式。当蓄电池向直流母线提供能量时,即S2导通,S1关断,双向DC/DC工作在BOOST模式。由于蓄电池对电流的纹波有严格的要求,如果电流纹波过大就会缩短电池的使用寿命,因此电池电流应该连续且纹波较小,所以两种工作模式下的变换器都应工作在电感电流连续(CCM)的状态。
2 双向BUCK-BOOST变换器分数阶数学建模
当双向DC/DC变换器的输入电压与负载维持恒定时,变换器的输出是由直流分量与周期性的纹波叠加而成,因此必须以DC/DC变换器的动态模型为基础分析才能抵消小信号扰动带来的影响,从而满足系统设计的要求。而通常是使用状态空间法来得出变换器的小信号模型。本文在采用电感和电容分数阶模型的基础上应用状态空间法来建立应用于储能系统的双向BUCK-BOOST的模型。
由文献[7]可知,实际中的电感和电容的分数阶模型为:
其中,α是电感的分数阶阶数且0<α<1;β是电容的分数阶阶数且0<β<1。
2.1 BUCK变换器的分数阶模型
当双向BUCK-BOOST变换器工作在降压模式即BUCK模式下时,负载为蓄电池能量从直流母线流向蓄电池,给蓄电池充电。在电感电流连续时,BUCK电路在每个开关周期内变换器有两个工作阶段,其开关周期为T,占空比为D。在0~DT阶段时,开关管S1导通;在DT~T阶段时,开关管S1关断。因此,BUCK变换器的两种不同工作模式下的分数阶数学模型为:
工作模式一(电路中开关管S1导通,即0 3 双向BUCK-BOOST变换器数值仿真 为了验证上述步骤所建立的分数阶模型的正确性,本文根据Matlab仿真软件以及改进的Oustaloup滤波器分数阶微分算法建立仿真模型。所选取变换器的参数为:直流母线电压:200 V;电池电压:60 V;开关频率:50 kHz。 3.1 BUCK-BOOST变换器分数阶数学模型与整数阶数学模型 首先根据BOOST变换器的数学模型建立其分数阶模型,分别得到电感电流和输出电压的仿真结果。BOOST变换器的整数阶模型实际上就是将分数阶模型的阶数换成1,通过仿真也得到了BOOST变换器的整数阶模型的结果,如图3所示。 通過比较可以看出,整数阶模型的电感电流纹波小、输出电压纹波也比较小,其值为ΔiL=0.17 A,Δvo=0.16 V。分数阶模型的电感电流纹波为ΔiL≈1.65 A,输出电压纹波Δvo≈7.7。而根据文献[7]和[9]可通过理论计算得出ΔiL=1.686 A,Δvo=7.77 V。可见,分数阶模型的数值仿真结果与理论计算的结果基本一致,而整数阶模型就相差较远。因此,采用分数阶模型可以更加准确地描述变换器的动力学行为。 同理再根据BUCK变换器的数学模型在Matlab/Simulink中建立其模型。其整数阶和分数阶的电感电流和输出电压仿真结果如图4所示。 3.2 BUCK-BOOST变换器分数阶与整数阶状态平均模型 根据BOOST变换器的数学模型建立其Matlab/Simulink分数阶状态平均模型。其整数阶和分数阶的状态平均模型的电感电流和输出电压仿真结果如图5所示。 根据BUCK变换器的数学模型建立其Matlab/Simulink分数阶状态平均模型,通过仿真也得出其整数阶状态平均模型和分数阶状态平均模型所得出的电感电流直流分量和输出电压直流分量的值是相等的,没有变化。 3.3 小结 由于实际电感电容是分数阶的,因此基于分数阶微积分理论建立面向储能应用的双向DC/DC变换器的分数阶模型。通过仿真结果,可以得出: (1)当双向DC/DC工作于BUCK/BOOST模式时,首先从仿真图可以看出其电感电流处于电流连续状态,符合我们之前的要求。然后,通过对BOOST变换器的电感电流和输出电压的理论计算,得出用分数阶建立变换器的模型时,更能符合变换器的本身的动力学行为,也会使以后的控制更加精确。 (2)通过用分数阶建模所得出的双向BUCK/BOOST变换器的传递函数(9)~(12)和(18)~(20),可以看出其都与电感电流的分数阶阶数和电容电压的分数阶阶数有关,因此,由于实际中电感、电容是分数阶的,所以建立分数阶模型更能准确地描述双向BUCK-BOOST变换器的特性。 (3)在实际应用中,储能一般用的是铅酸蓄电池,而其对充电电流的纹波有着很严格的要求,过大的电流纹波会影响电池的使用寿命,在充电过程中电池电流应该连续并且电流纹波要在电池规定的纹波系数范围内。而如果用整数阶对双向DC/DC进行建模分析时,不能够准确地描述电感电流和输出电压的纹波大小,这在实际控制时可能会对蓄电池造成损坏。 4 结 论 以往用整数阶电感电容模型来等效代替实际电感电容对电路进行分析时有一定的误差,而且在器件刚导通时刻超调量远大于实际模型,当分数阶数值小于1更接近于0的情况下误差越大,甚至有可能导致错误的分析结果。所以,应该选择分数阶建模更加准确地描述变换器的动力学行为。 参考文献: [1] 王立乔,孙孝峰.分布式发电系统中的光伏发电技术 [M].北京:机械工业出版社,2004. [2] 陈瑞杰.储能系统双向直流变换器及其控制策略研究 [D].哈尔滨:哈尔滨工业大学,2014. [3] 于月森,戚文艳.Buck-Boost变换器的环路补偿及仿真 [J].电测与仪表,2014,51(8):91-94+106. [4] 陈静.锂电池/超级电容混合动力系统及控制策略 [J].电测与仪表,2016,53(2):52-56. [5] TOLBERT L M,PETERSON W A,WHITE C P,et al. A Bi-directional DC-DC Converter with Minimum Energy Storage Elements [C]//Conference Record of the 2002 IEEE Industry Applications Conference. 37th IAS Annual Meeting(Cat.No.02CH37344).Pittsburgh:IEEE,2002:1572-1577. [6] 程思,胡涛,刘崇刚.基于双向DC/DC的混合能源系统设计研究 [J].电力电子技术,2016,50(11):5-7+10. [7] WANG L L. A New Control Strategy of Hybrid Battery/Ultra-capacitor Energy Storage in Electric Vehicle [C]//Proceedings of 2016 2nd International Conference on Mechanical,Electronic and Information Technology Engineering(ICMITE 2016).Chongqing:DEStech Publications,2016:11. [8] 张鹏超.双向变换器在混合储能系统中的应用研究 [J].电源技术,2015,39(11):2531-2533. [9] 罗咏.双向DC/DC变换器及电池能量管理系统研究 [D].武汉:华中科技大学,2013. [10] 王发强,马西奎.电感电流连续模式下Boost变换器的分数阶建模与仿真分析 [J].物理学报,2011,60(7):96-103. [11] 孙会明,陈薇,孙龙杰,等.Buck变换器的分数阶仿真模型与混沌分析 [J].现代电子技术,2014,37(24):154-159+ 162. 作者简介:李娜(1993—),女,汉族,陕西宝鸡人,助教,硕士研究生,主要研究方向:光电系统与控制。 收稿日期:2021-03-17 基金项目:山东华宇工学院2020年度教育教学改革研究项目(2020ZD06)
