时滞影响的两轮自平衡小车的PID控制研究

南京林业大学 张子璇 解文周 台永鹏

两轮自平衡小车本质是一种倒立摆，其控制原理为关键技术。考虑控制器、传感器、驱动电机在平衡控制中的延迟现象，建立了两轮自平衡小车的动力学模型，采取PID控制算法和Smith预估校正模块的平衡策略，通过Simulink进行仿真研究。讨论了阶跃与正弦信号下时滞对小车的影响以及PID的控制效果。发现在控制环节中加入Smith预估校正模块，能有效减小时滞的影响，得到更好的控制效果。

两轮自平衡小车是一个典型的静态不稳定系统，具有控制灵活、结构简单的特点。其本质是一种倒立摆，在控制领域常常作为典型的控制系统来研究。

目前两轮自平衡小车的平衡控制，常用方法有模糊控制、遗传算法控制以及PID控制技术等。模糊控制在参数整定上较困难而遗传算法的计算量较大，在实时控制以及时滞的应用很难实现，通常用于离线状态的参数优化设计。时滞是指信号传输过程中的延迟，是广泛存在于自然界中的一种物理现象。文中考虑了控制器、传感器、驱动电机在平衡控制中的延迟现象，主要研究阶跃信号与正弦信号输入对自平衡小车平衡控制的影响，并根据系统的鲁棒性和响应性调节PID控制器的参数，加入Smith预估校正模块以期获得良好的控制效果。

1 两轮自平衡车动力学模型

自平衡小车的平衡控制主要是针对前进时的前后倾倒。在实际过程中的运动十分复杂所以我们需要提出合理的假设：（1）不考虑零部件之间的摩擦力和内部能量损耗。（2）不考虑直流电动机空载阻转矩，电动机输出转矩直接为电磁转矩。（3）小车的车轮和车体均为刚体。如图1示以两轮轴线方向为y轴，车体前进方向为x轴，过车轮轴中点竖直向上为z轴，建立坐标系。图中M为车轮质量，m为车体质量，L为质心到车轮轴线的距离，r为车轮半径，Tc为外界给车体的转矩，θ为车体转过的角度，Mω为电机给车轮的转矩，Mb为电机给车体的转矩，φ为车轮转过的角度，Ff为地面给车轮的摩擦力。Fx，Fy，Fz分别为车轮组件在x，y，z轴方向上给车体的力。对车轮和车体进行受力分析，电动机对小车车轮的扭矩与电动机对小车车体的扭矩大小相等，方向相反，即Mω=Mb=u。根据牛顿第二定律，得到动力学方程：

图1 受力示意图

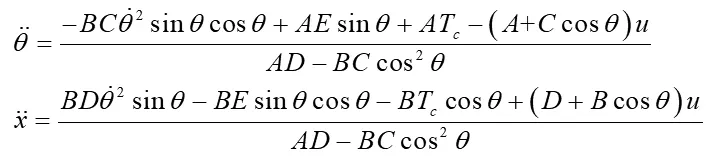
其中A=Iω/r+mr+Mr，B=rmL，C=mL，D=Ib+mL2，E=mgL，Iω为车轮的转动惯量，Ib为车体的转动惯量。

2 两轮自平衡小车的控制模块的建立

文中两轮自平衡小车被控对象为车身倾角，根据倾角传感器检测到的倾角，通过PID控制器来调节电动机带动转子盘旋转，转子盘对车身的反作用力矩使车身平衡。我们考虑时滞的影响建立PID控制仿真模块并对其进行分析。可以根据系统的响应性和鲁棒性调节PID控制器的参数。调节参数Kp=-275，Ki=0，Kd=-18时，系统的控制效果较好。当时滞较大时仅仅利用PID不能得到很好的控制效果，可以加入Smith预估控制模块以期得到更好的控制。图2所示为Smith预估控制模块。

3 仿真分析

3.1 阶跃信号下不同延迟时间的仿真分析

图3(a)所示为作用1s的阶跃信号得到不同延迟时间的角度变化曲线。图中无延迟时最大的倾斜角度约为0.235rad，5.8s后逐渐平衡；延迟时间为0.006s时的最大倾斜角度为0.239rad，平衡时间为6s；延迟时间为0.02s时的最大倾斜角度为0.25rad，小车在8s后平衡。随着延迟时间的增加，小车的最大倾斜角度增加，平衡所需要的时间也增大。图3(b)所示为在上述阶跃信号下加入预估控制模块，延迟时间为0.02s时不同提前预估时间的角度变化曲线图。图中无预估控制时倾斜角度为0.25rad；预估时间为0.02s时最大倾斜角度为0.232rad，平衡时间约为6s；提前预估0.04s时倾斜角度为0.225rad，平衡时间约为5s。

图3 角度变化曲线图

3.2 正弦信号下不同延迟时间的仿真分析

图4(a)为1s的正弦信号得到不同延迟时间的角度变化曲线。图中没有延迟时最大倾斜角度为0.047rad，5.8s后回平衡状态；延迟时间为0.006s时最大倾斜角度为0.048rad，5.9s后回到平衡状态；延迟时间为0.02s的最大倾斜角度为0.052rad，8s后回到平衡状态。图4(b)为在上述正弦信号下加入预估控制模块，延迟时间为0.02s时不同提前预估时间的角度变化曲线图。提前预估0.02s和0.04s的最大倾斜角度分别为0.048rad和0.044rad，平衡时间约为6s。与无预估控制时相比较倾斜角度和平衡时间都减小，得到了很好的控制效果。

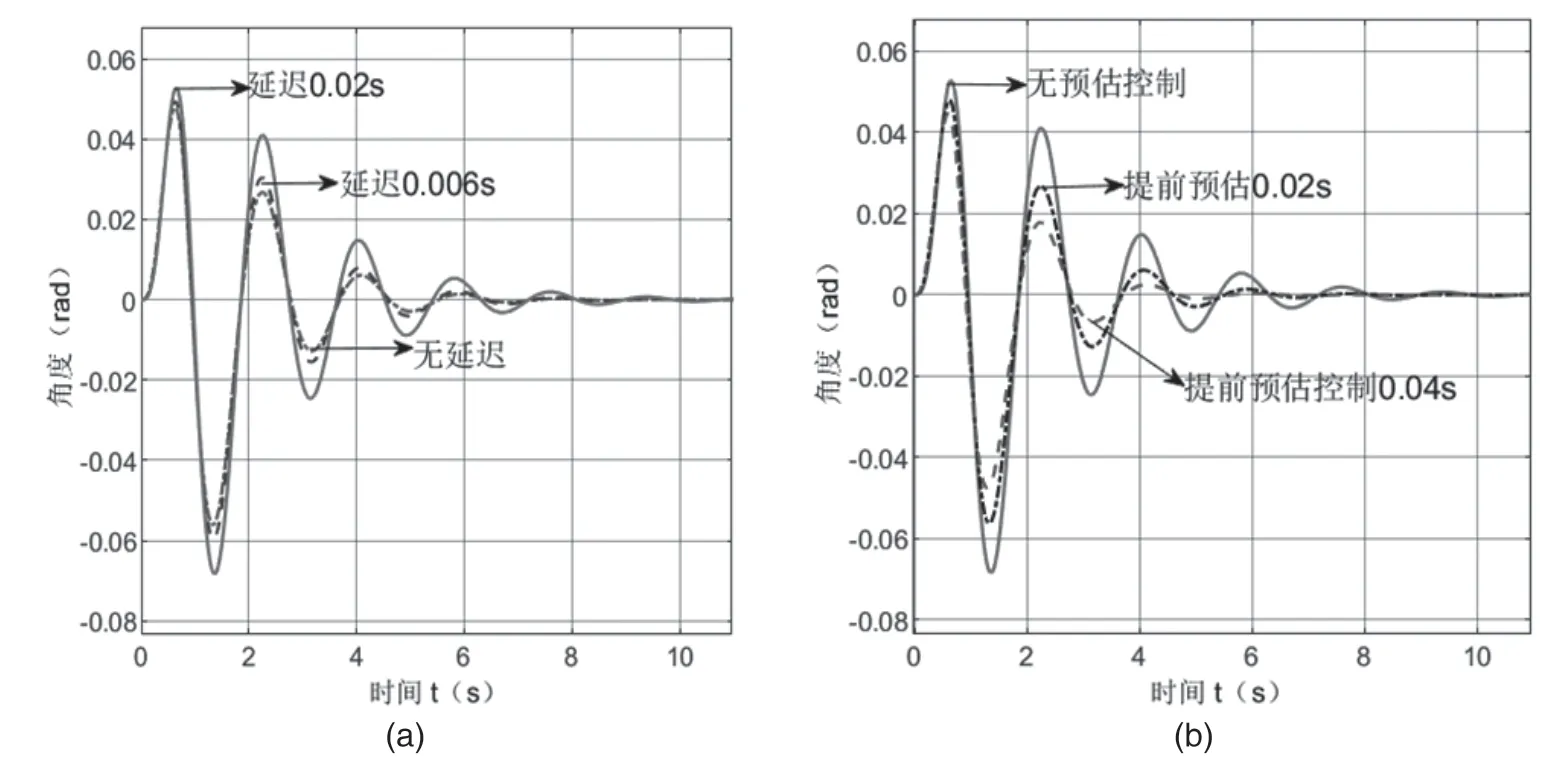
图4 角度变化曲线

二轮自平衡小车是静态不稳定、动态稳定的系统，具有非线性、多变量等特点。本文采取PID控制的平衡策略，对时滞影响的两轮自平衡小车进行了动力学建模并利用了PID控制，同时加入了Smith 预估校正模块对其仿真分析。在阶跃信号下，延迟时间为0.02s的最大倾斜度为0.25rad，平衡时间为8s。在正弦信号下，延迟0.02s时最大倾斜角度为0.052rad以及平衡时间为8s。由此知在该PID控制器的控制下小车受突然的外力，倾斜角度较小同时能在较短的时间内回到平衡状态。此PID控制器的控制效果很好。加入了Smith预估控制模块对时滞影响进行提前预估。随着预估时间的相应增加小车的倾斜角度减小，回到平衡状态的时间也缩短。Smith预估控制模块使得小车的自平衡控制得到了很好的改善。