直接分析法在异形钢结构设计中的应用及其与计算长度系数法的对比
2021-11-03高鸣,田金
高 鸣, 田 金
(北京市建筑设计研究院有限公司, 北京 100045)
1 钢结构稳定设计方法简述
受压稳定通常是钢结构受压构件设计的控制性因素。传统钢结构设计方法将内力分析和构件设计拆分为两个步骤,构件内力基于整体结构的一阶线性分析,在构件设计时引入受压稳定系数来考虑结构的二阶效应及结构初始缺陷、残余应力等因素,而受压稳定系数的确定,关键在于构件计算长度系数的确定。因此,传统设计方法也被称为“计算长度系数法”。
长期以来,我国钢结构及空间结构类设计规范[1-4]仅对钢框架、门式刚架以及体系成熟、形式常规的网架、网壳、桁架结构给出杆件计算长度系数。对于大量形态各异、体系不甚明确的异形钢结构,当采用传统方法设计时,仍面临着如何确定构件计算长度系数的难题。
基于此,2018年我国实施的《钢结构设计标准》(GB 50017—2017)[2](简称新钢标)引入了近年国际上发展起来,并逐渐成为主流钢结构稳定设计方法的“直接分析法”(direct analysis method,DM)[5-6]。该方法在内力分析阶段直接引入结构整体缺陷及构件缺陷,并采用二阶非线性分析法来考虑P-Δ和P-δ效应,从而将原来的稳定问题转化为强度问题。
新钢标颁布至今,关于直接分析法在钢框架、网壳、空间折板等类型钢结构中的应用方面,国内学者、工程技术人员已有一定研究[7-9]。本文以某水上乐园工程中“海星”造型的异形钢构架为例,介绍了直接分析法在异形钢结构设计中的应用。
2 工程背景
某水上乐园项目入口处为其主要的景观节点,其建(构)筑包括入口大门和大门两侧的游客服务中心。根据乐园主题设计效果,入口大门按“飞鱼”造型包装,两侧的游客服务中心外部按“海星”造型包装。入口建筑整体效果见图1。

图1 入口建筑整体效果图
按照建筑设计,“海星”需与其下部的单层建筑脱开不粘连,其结构应能自成体系、独自受力。经与建筑师协调,在不影响建筑效果的前提下,可在建筑物顶部给“海星”设置少量竖向支点,以减小“海星”跨度。
“海星”主体结构采用钢结构,由顶盖和5条落地支腿组成,见图2。为方便异形结构找形,结构杆件均采用圆钢管,钢管间为相贯焊接,落地支腿底部按铰接设计。“海星”钢结构内、外均包裹2cm厚钢筋铁丝网泥塑表皮,每平米重0.25kN。以入口东侧“海星”为例,该“海星”结构高约7m,长约20m,宽约8m,落地支腿间的距离约7~16m。结构主要构件采用φ140×8钢管,局部受力大的部位采用φ180×10,联系构件采用φ60×5。
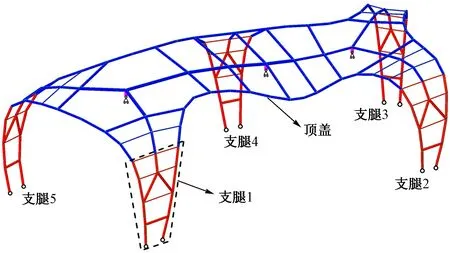
图2 东侧“海星”结构三维简图
“海星”结构为异形钢结构,当采用传统的计算长度系数法进行设计时,无法套用现行设计规范来确定构件的计算长度系数。而直接分析法为这一类型结构的设计提供了便利。
3 直接分析法设计过程
采用直接分析法进行钢结构设计的基本流程为:建模、施加静力荷载→线性屈曲分析→施加整体初始缺陷→施加构件初始缺陷→地震时程选择→非线性分析工况定义→分析求解→构件强度校核。本工程采用MIDAS Gen软件进行设计,以下介绍上述流程中的关键步骤在MIDAS Gen软件平台下的实现。
3.1 线性屈曲分析与整体初始缺陷的施加
采用1.0恒载+1.0活载作为初始荷载进行线性屈曲分析,得到“海星”结构第1阶屈曲模态见图3。
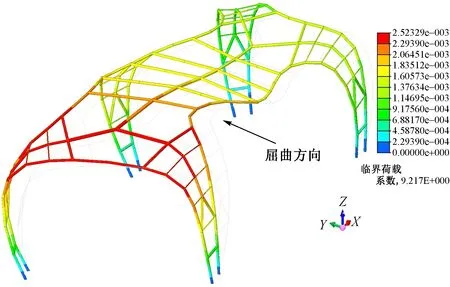
图3 “海星”结构第1阶屈曲模态
从第1阶屈曲模态可以看出,“海星”结构整体失稳模式为侧向失稳,与钢框架结构类似,因此,可按新钢标第5.2.1条取H/250(H为结构总高度,本工程为7 000mm)作为整体缺陷幅值。利用MIDAS Gen的“根据初始缺陷更新模型”功能(图4),按照第1阶屈曲模态施加整体缺陷最大值28mm。若结构失稳模式接近于网壳类结构,可按《空间网格结构技术规程》(JGJ 7—2010)[4]第4.3.3条取跨度的1/300作为幅值施加整体缺陷。
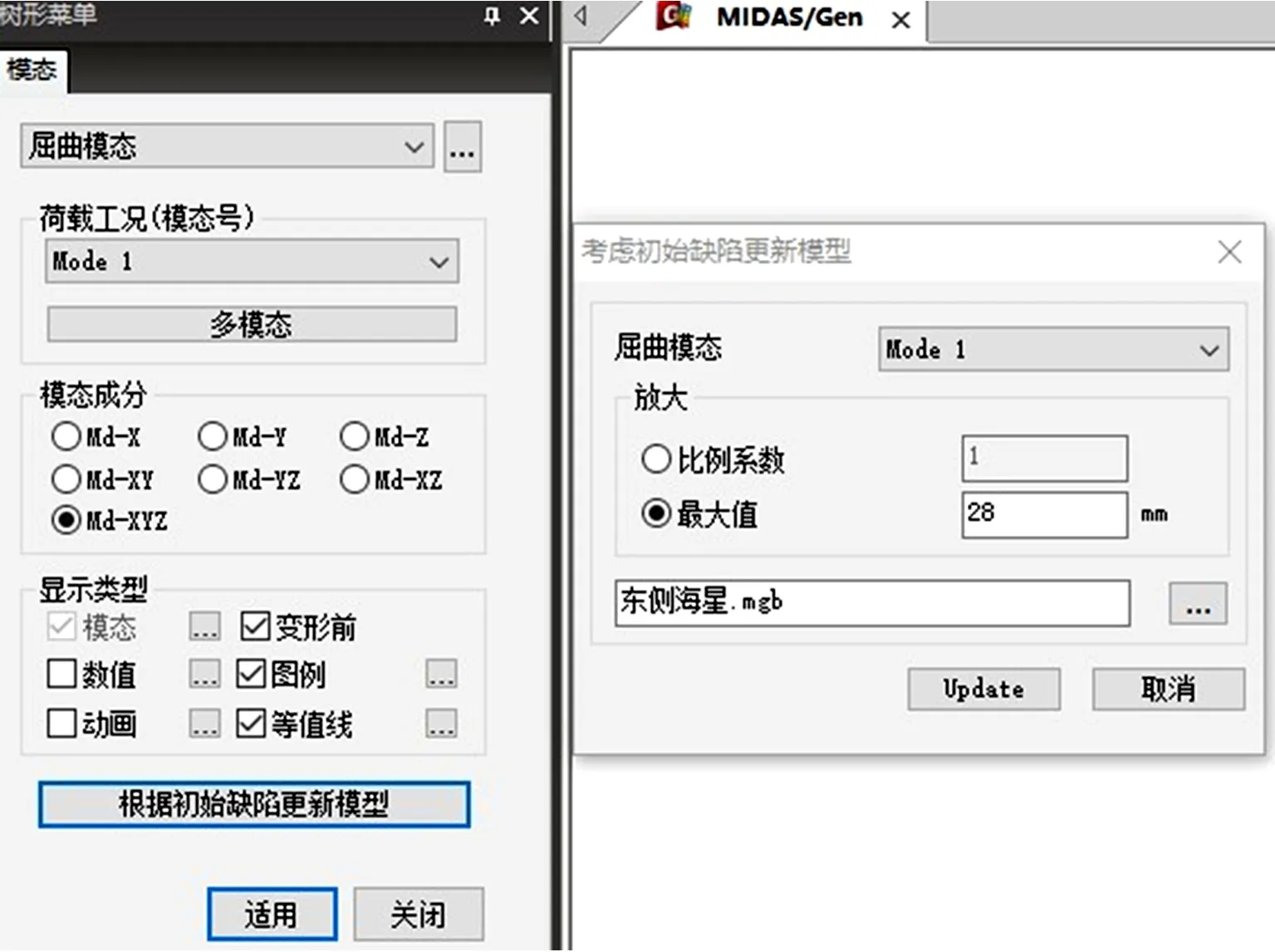
图4 MIDAS Gen中整体初始缺陷施加对话框
3.2 构件初始缺陷的施加
依据新钢标第5.2.2条,本工程采用不考虑材料塑性发展的直接分析法(即仅考虑几何非线性,不考虑材料非线性),构件初始缺陷按等效几何缺陷的方式施加,构件中点的初始变形按综合缺陷代表值施加。本工程圆钢管均采用热轧无缝钢管,截面类型为a类,构件综合初始缺陷代表值e0/l取1/400。
因MIDAS Gen软件目前尚无自动施加构件初始几何缺陷功能,故应用时需将构件人为分段(一般可分为4段),再对分段后生成的杆中节点按照正弦半波的波形,在垂直于杆轴的方向偏移。本工程使用Rhino平台下的Grasshopper参数化插件,编制了杆件分段及杆中节点偏移程序。图5给出了各杆中节点偏移向量,为了便于显示,对图中向量做了放大处理。偏移方向可依杆件单元局部坐标方向在垂直于杆轴的平面内任意选定,本工程每45°取一个偏移方向,考虑了8个方向的计算包络,即建立了8个初始缺陷模型进行包络计算。
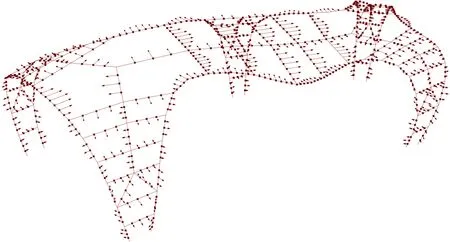
图5 “海星”结构构件初始缺陷偏移向量图
用偏移后的节点坐标来更新MIDAS Gen模型节点坐标,即完成了构件初始缺陷的施加。
3.3 地震时程的选择
直接分析法属于非线性分析法,不能使用振型叠加法来计算地震作用,而应使用地震波进行时程分析。本工程建设地设计基本地震加速度为0.15g,场地特征周期Tg为0.65s,按照《建筑抗震设计规范》(GB 50011—2010)[10]第5.1.2条规定,通过控制结构基底剪力的方式选定两条天然波(TH003TG065_CHI-CHI,TH017TG065_CHI-CHI)和一条人工波(RH2TG065)对结构进行包络设计。
3.4 非线性分析工况的定义与分析
与线性分析法可对各单工况荷载分别独立分析再线性叠加的方式不同,非线性分析法应将各单工况荷载先组合为荷载组合后,再对每一个荷载组合分别进行非线性分析。对于静力荷载组合,可用MIDAS Gen的“使用荷载组合建立荷载工况”的功能(图6)生成用于非线性分析的荷载工况。对于包含地震作用的荷载组合,应先将静力荷载转换为逐步加载的时程荷载(图7),再接续地震波时程进行完整非线性分析求解(图8)。
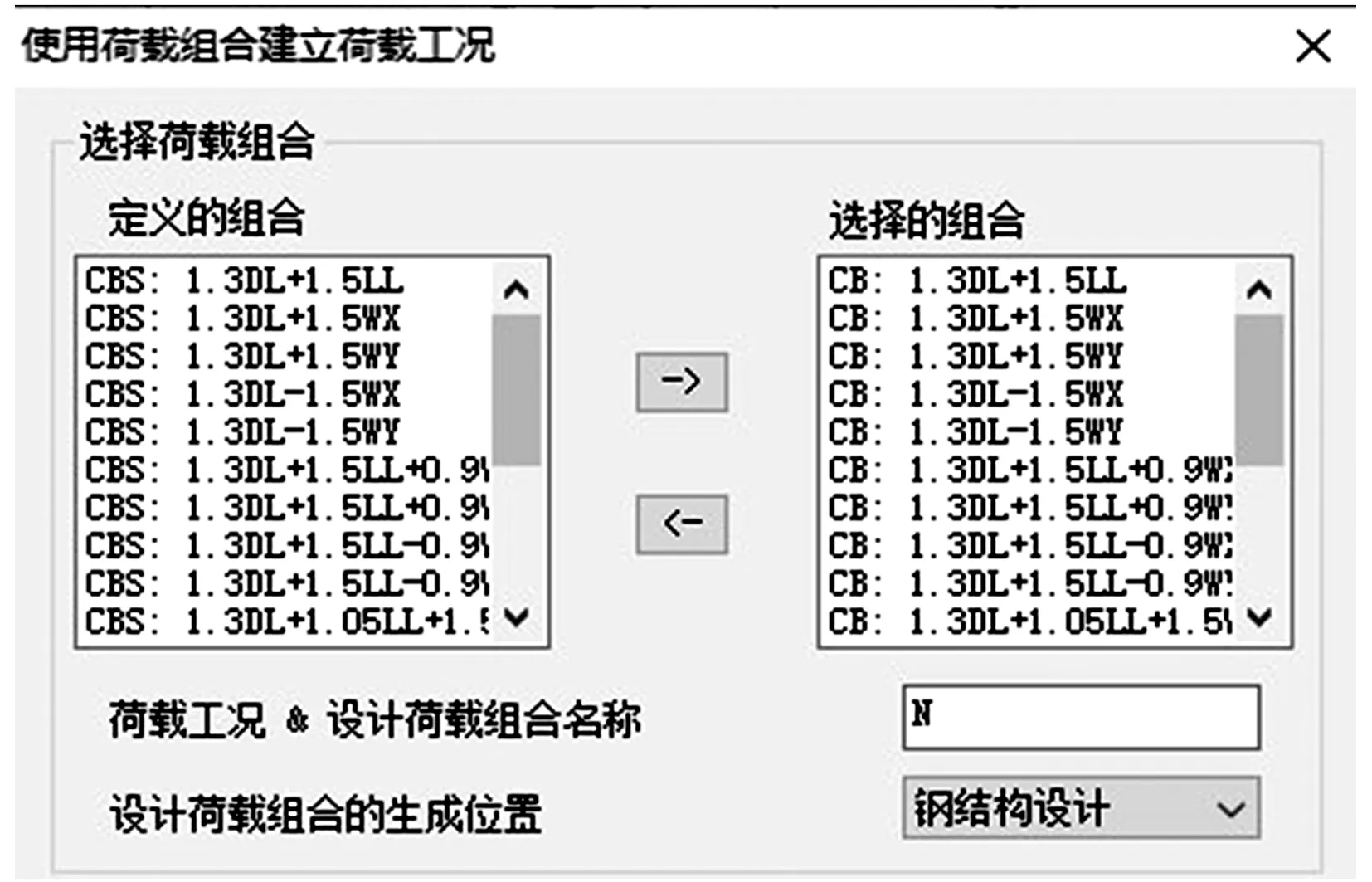
图6 使用荷载组合建立荷载工况对话框
图7 静力荷载转换为时程荷载定义对话框
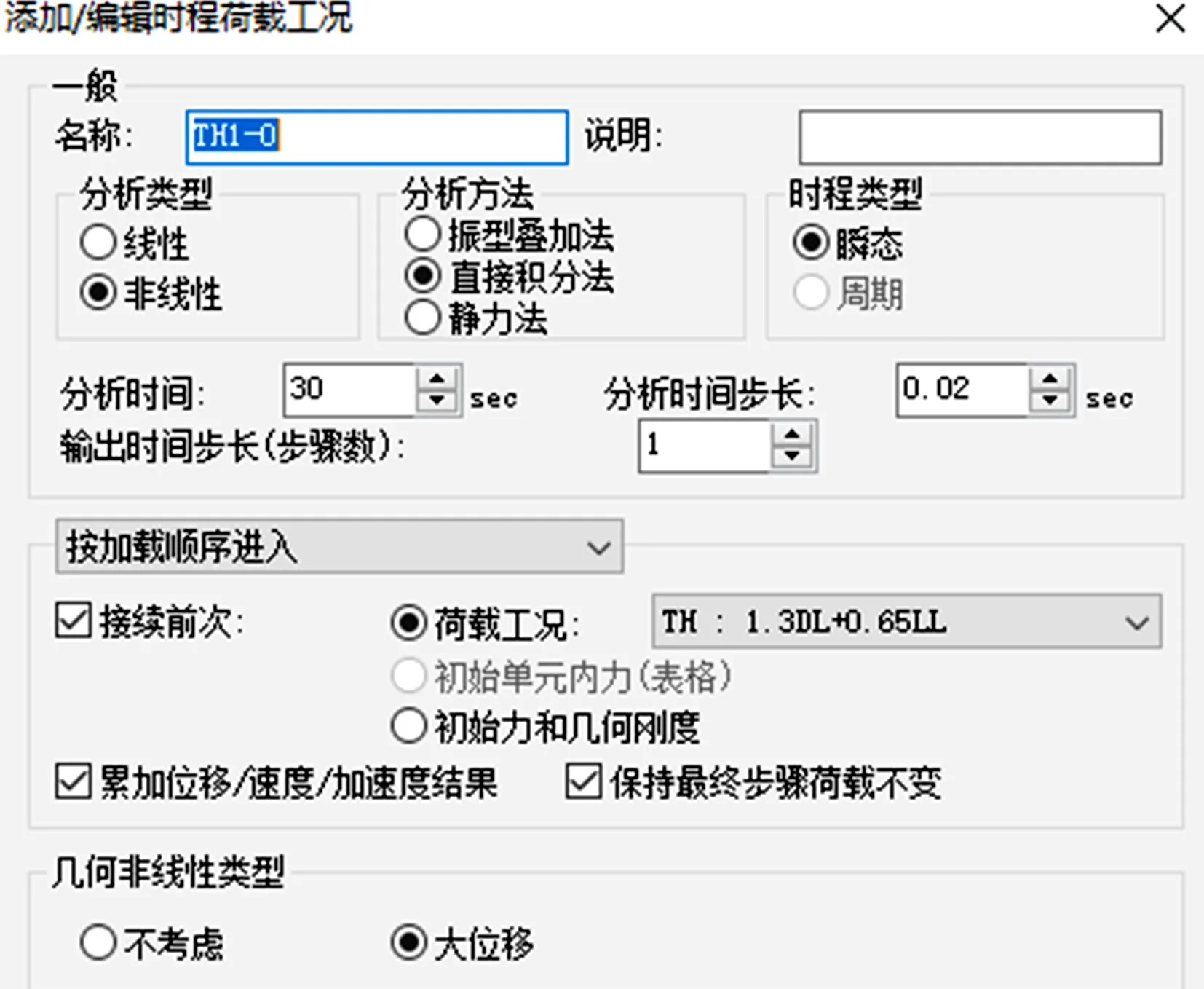
图8 静力荷载时程接续地震波时程定义对话框
3.5 构件强度校核
采用MIDAS Gen进行构件设计时,可仅提取其强度计算结果进行构件截面强度校核。也可将控制构件受压稳定验算的计算长度系数μ设(MIDAS Gen中表示为“K”)为一极小值,而将控制构件受弯稳定验算的整体稳定系数φb(MIDAS Gen中表示为“phi_b”)设为一极大值,使其稳定验算应力比不起控,此时可采用综合应力比进行构件截面强度校核。
4 基于屈曲分析的计算长度系数法
如图2所示,“海星”结构由顶盖和5根支腿组成。顶盖部分主要承受弯矩,可按梁设计,对于圆管截面,整体稳定系数φb取为1.0。支腿部分可视为曲面双肢格构柱,承受压力和弯矩,压力通过两侧的曲线型分肢竖管传至落地支座,而分肢竖管的计算长度是其受压稳定验算的关键性参数。
如第1节所述,分肢竖管的计算长度系数无法通过规范直接得到,对于此类结构,一般通过屈曲分析[11]来求得计算长度系数。在进行屈曲分析时,通常是在受压构件顶部施加节点单位力作为屈曲初始荷载。此法应用于本工程曲线型分肢竖管时,将导致各分段杆件轴力不均匀(典型支腿轴力分布如图9(a)所示),不便于确定欧拉临界力。
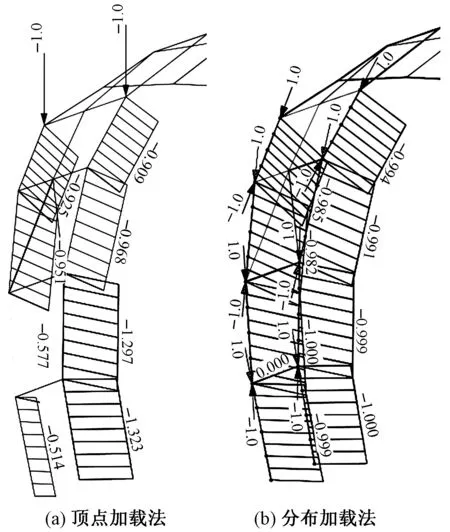
图9 支腿5屈曲初始荷载施加方式及轴力分布
本文提出一种新的适用于曲线受压构件的分布式屈曲初始单位力施加方式,即在各分段杆件的两端施加一对指向杆中的单位节点力,并将各分段杆件进行单元细分。应用这种加载方式,本工程曲线型分肢竖管轴力较为均匀(图9(b)),临界荷载系数即为欧拉临界力。
在整体模型中对各支腿分别进行屈曲分析,典型支腿面外、面内第1阶屈曲模态分析结果见图10。得到各支腿欧拉临界荷载Pcr后,根据欧拉公式:
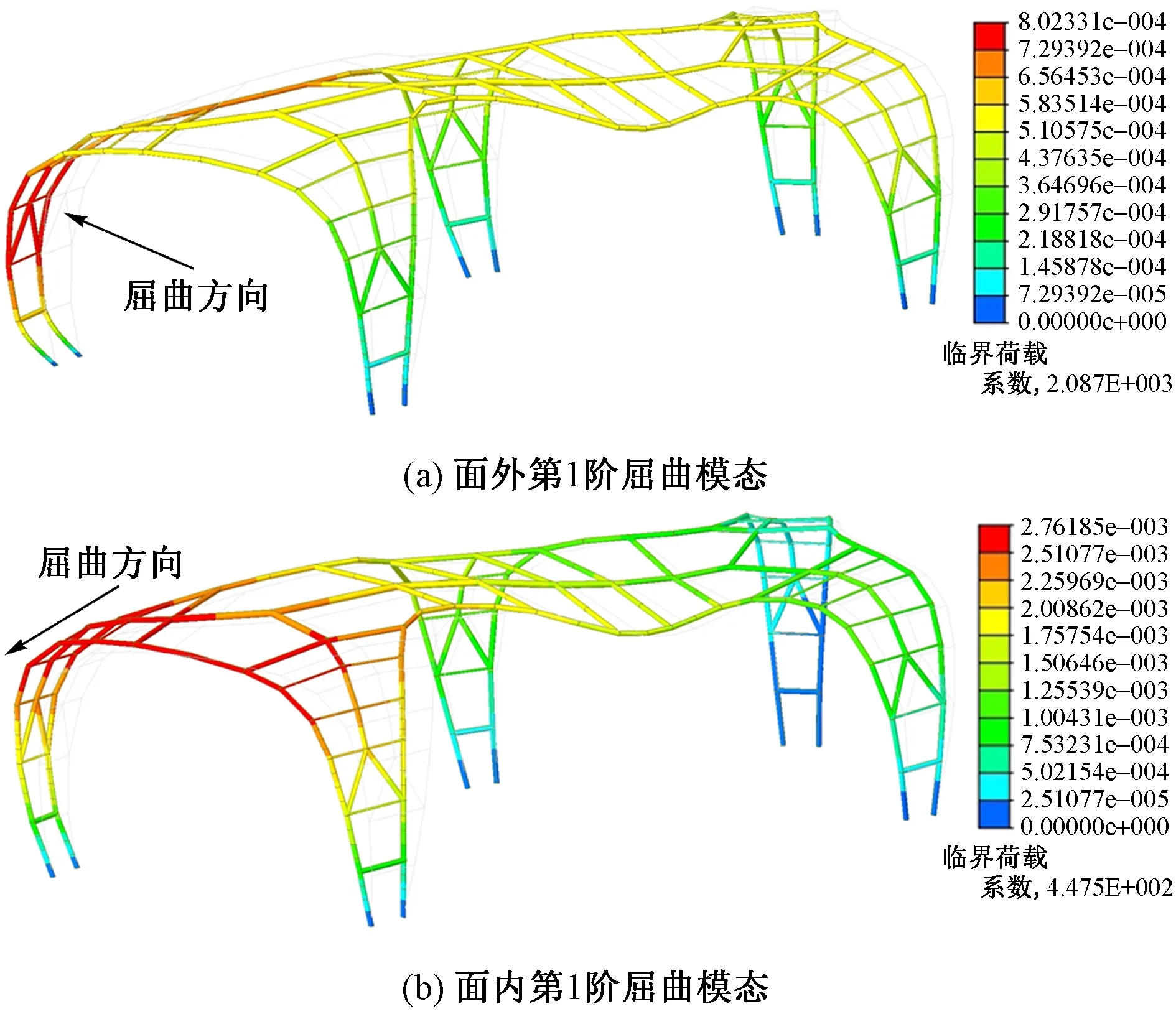
图10 支腿5面外、面内第1阶屈曲模态分析结果
Pcr=π2EI/(μl)2
可得计算长度μl,结果见表1。将各支腿计算长度除以各段杆件(每个分肢4段)的长度,即得到该段杆件的计算长度系数,面外为2.90~5.34,面内为1.66~2.99。
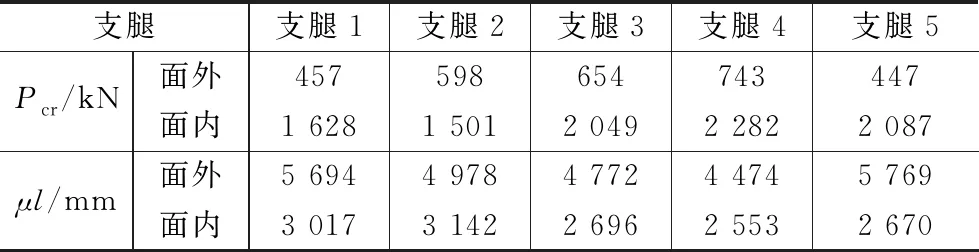
各支腿欧拉临界荷载和计算长度 表1
需要指出的是,“海星”结构在实际的静力荷载作用下,各支腿分肢竖管轴力是不均匀的,且其分布规律与假定屈曲初始荷载的顶点加载法也不相同。所以无论是顶点加载法还是分布加载法,都是用近似的方式来求得杆件的计算长度系数。
5 结果与对比
分别采用直接分析法和计算长度系数法对本工程中“海星”钢结构进行验算,其中,计算长度系数法的地震作用采用反应谱法计算。两种方法得到的各杆件应力比结果见图11,其差值在-0.08~+0.12之间,平均仅相差0.01,计算结果十分接近。经分析,本例中大约50%~60%的杆件应力比为地震组合控制,其余为静力荷载组合控制,这说明了本例所用两种方法的适用性与正确性。
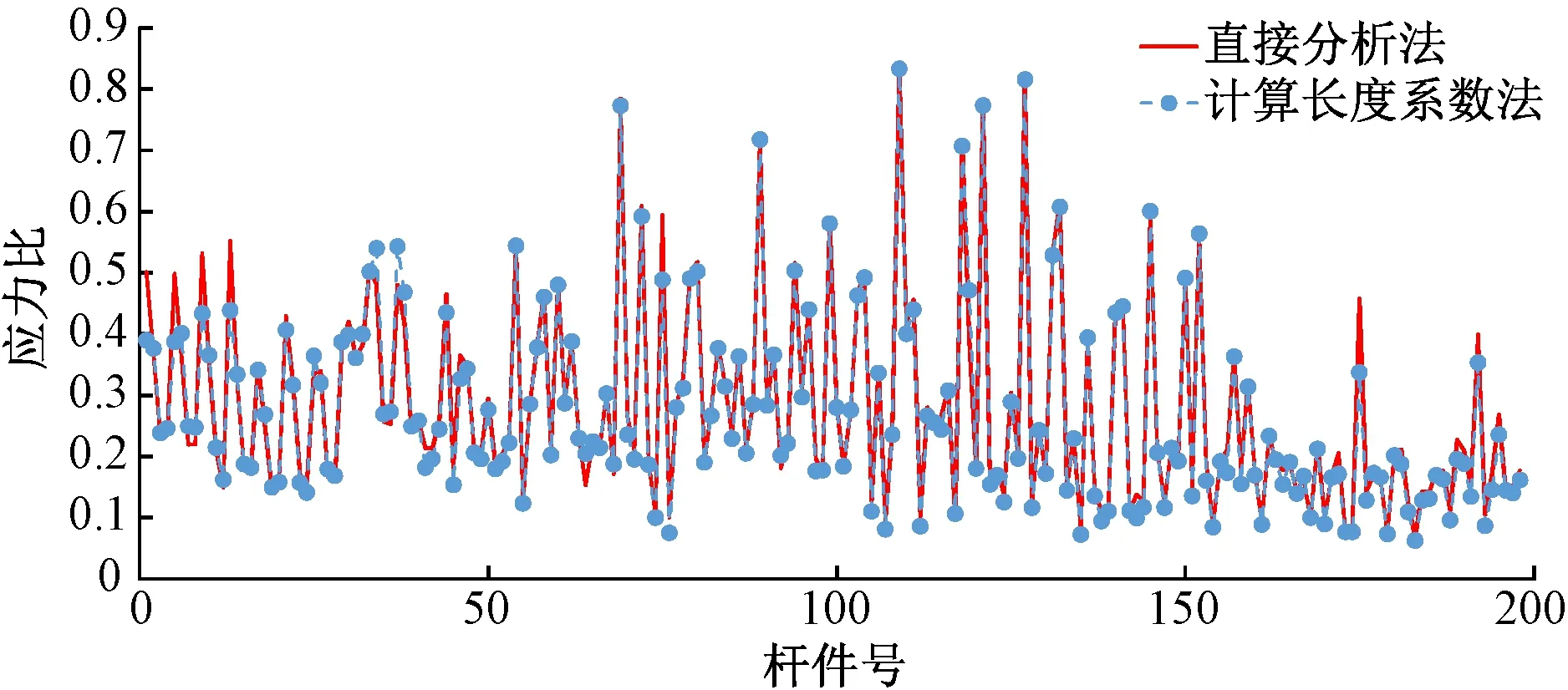
图11 直接分析法和计算长度系数法杆件应力比计算结果对比
需要指出的是,本例虽通过引入分布式屈曲初始单位力施加方式求得到了曲线型支腿杆件的计算长度系数,但前提是“海星”结构还是能够较为清晰地从受力的角度出发,分成受弯顶盖和受压支腿,采用计算长度系数法时仅需对支腿结构进行屈曲分析即可。当遇到无法在受力上清晰分割的异形钢结构时,将难以应用基于屈曲分析的计算长度系数法。而直接分析法无需区分构件受力特性,受弯、受压和受拉杆件设计过程完全一致,可十分方便地应用在异形钢结构的设计中。本文所列举“海星”结构虽然简单,但其基于MIDAS Gen的直接分析法步骤与要点却与任意异形钢结构无异,该法可在异形钢结构中推广应用,所采用的软件平台也可以是其他通用结构有限元软件,如SAP2000,3D3S等。
6 结论与展望
应用直接分析法进行异形钢结构分析与设计克服了传统计算长度系数法不易确定构件计算长度系数的缺点,且计算结果与计算长度系数法吻合,可在任意异形钢结构设计中推广。
除了个别软件[12]外,目前市面上主流的通用结构设计软件均未实现自动施加构件初始几何缺陷功能,虽利用自编程序、二次开发可实现杆件节点偏移,但过程较为繁琐。若主流商用软件能添加该功能,则对直接分析法的应用能起到较大的推动作用。
理论上,一个结构体系中的任何一根杆件的变化均会对所有杆件内力的产生影响。为方便起见,本文应用直接分析法时,某一杆件初始几何缺陷的施加仅考虑其对自身的受力影响,而忽略对其他杆件的影响,即便如此,由于最不利初始几何缺陷方向的未知性,在设计时也需要进行多个(本文取8个)偏移方向模型的包络计算,工作量大。由圣维南原理可知,某一杆件的内力主要受其相邻杆件的影响。假定某一杆件有N根相邻杆件,其自身及相邻杆件均考虑8个偏移方向角的情况下,要确定该杆件的最不利内力,应进行8(N+1)个模型的包络计算。假定某一结构体系有M根杆件,每根杆件平均有N根相邻杆件,则确定所有杆件最不利内力则需要进行M×8(N+1)个模型的包络计算,计算量巨大。在计算精度可为工程设计接受的前提下,如何快速得到杆件在初始几何缺陷模式下的最不利内力或可作为进一步发展直接分析法的研究方向之一。
